停止损失序的性质及其在风险管理中的应用

王丙参，魏艳华（天水师范学院 数学与统计学院，甘肃 天水 741001）

停止损失序的性质及其在风险管理中的应用

王丙参，魏艳华
（天水师范学院 数学与统计学院，甘肃 天水 741001）

给出一些常见随机序的定义并解释了经济含义，研究了停止损失序的性质及与其他随机序的关系，给出保险精算中常用的停止损失随机序的确定方法及应用，对风险模型进行随机比较，最后利用随机序探讨了停止损失再保险.

停止损失序；风险；再保险

对风险进行认识及研究，一直就是金融与保险中的重要内容之一.以前，人们都是给出风险的量化指标，但一直无法找到共识的度量方法，随机序的出现解决了此问题.目前，随机序被进一步引入到最优再保险、破产理论、生存分析等问题中，并成为保险精算研究人员分析风险问题的重要工具.保险人在选择承保风险、再保险形式及构建投资组合的时候及投保人在寻找最优的自留额时，都要对风险的相对优劣进行评估，这实际就是风险排序.停止损失序与停止损失再保险联系密切，目前关于这方面的文献很多，但都不系统，所以有必要对停止损失序给予详细的系统探讨.［1-4］签于此，本文首先给出一些常见随机序的定义，并解释了其经济含义，研究了停止损失序的性质及与其它随机序的关系，给出保险精算中常用的停止损失随机序的确定方法及应用.

1　停止损失序性质及与其他随机序的关系

定义1［5-7］如果非负随机变量X，Y表示风险，令，则有

（1）称Y大于X，记为X≤stY，若对， FX（x）≥FY（x）或¯X（x）≤¯Y（x）；

等价定义：对于非负随机变量X，Y，若存在一对（X′，Y）使得X′～X且P（X′≤Y）=1，则称X≤stY.

（2）称X按停止损失序小于Y，记为X≤slY，若对∀d≥0有

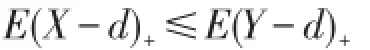
或

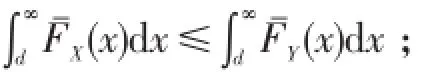
（3）称X按α阶停损序小于Y，记为X≤sl（α）Y，若对有

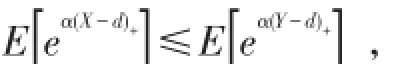
或

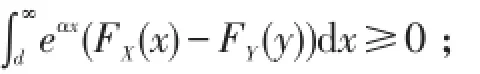
（4）称Y的尾重于 X的尾，记为 X≤ttY，若EX=EY，且存在x0∈R，使得

但

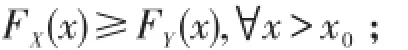
（5）称风险X≤hY，若对，h（x）是［0，+∞）上非减、可导的正函数且使得下述不等式两端均有限，

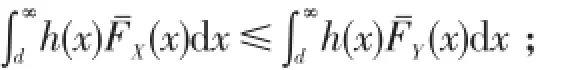
较重的尾指该随机变量取大值概率大，这使得该风险与具有相同均值的风险相比没有优势，因为该风险取值更广，从而降低可预见性，即指危险性较大.

显然，对任意随机变量X有 μ=EX≤cx（≤sl）X；若X≤sl（α）Y，则X≤sl（β）Y，∀β≥α；

序≤h满足半序的自反性、对称性、传递性，是风险族上的一个偏序.当h（x）=c＞0时，则由X≤hY可得

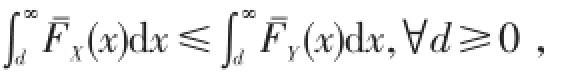
从而得到X≤stY；

当h（x）=erx，若对∀r＞0有X≤hY，

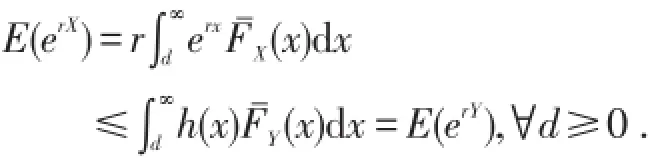
从而可得指数序X≤expY；

定理1（1）X≤stY⇔ 对一切递增函数 f，有E［f（X）］≤E［f（Y）］；

（2）X≤slY⇔ 对一切非降下凸函数 v，有E［v（X）］≤E［v（Y）］⇔ 对一切非降上凸函数u，有E［u（X）］≥E［u（Y）］.

证明 因为（1）（2）证明方法类似，为简单起见，所以只证明（1）：

充分性 令 f-1（a）=inf｛x；f（x）＞a｝，则

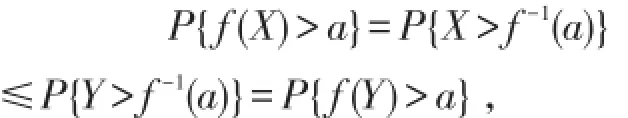
从而f（X）≤stf（Y），即

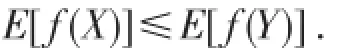
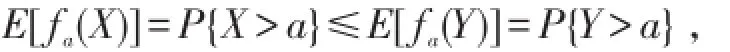
由此可见X≤stY.

定理2（1）对两风险X，Y和随机变量Θ，如果对∀θ∈Θ有

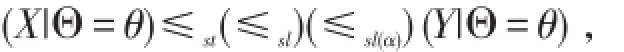
则有

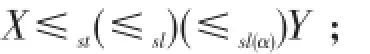
（2）如果对每个Xi≤st（≤sl，≤sl（α））Yi，i≥1，计数变量

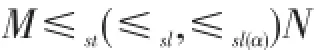
且所有变量相互独立，则

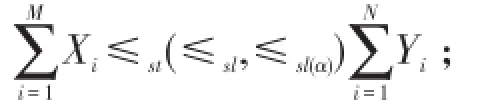
证明（1）显然成立；

（2）可由概率论中强实现定理得≤st成立.

下证≤sl成立：对∀X，Y，Z，如果Z独立于X，Y 且X≤slY，则有

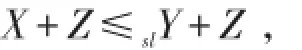
因此有

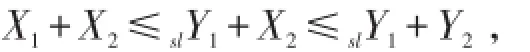
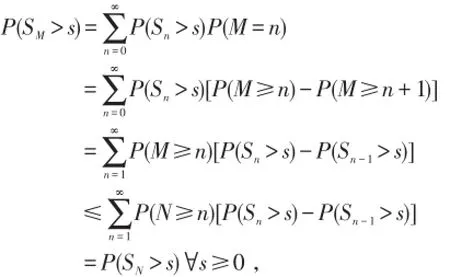
即SM≤slSN，结论成立.

下证≤sl（α）成立：只证n=2，且X2，Y2有相同的分布函数H的情形，其余情形同理可得；设X，Y分别有分布函数F，G，则对有

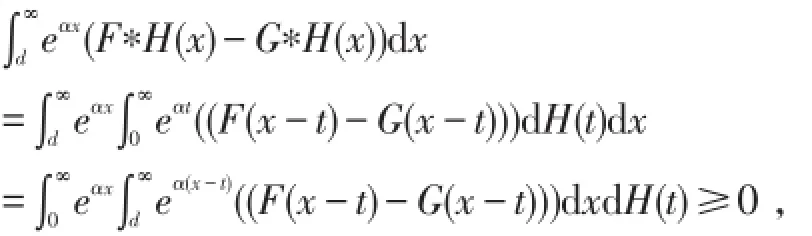
结论≤sl（α）成立.证毕.

定理3［5］（1）（泛函不变性）若X≤slY，则对∀非降下凸函数φ（x）有φ（X）≤slφ（Y）.特别地

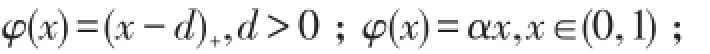
（2）（分离定理）若X≤slY，则存在Z使得

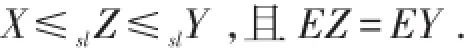
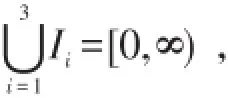
定理5设分布函数Fy，Gy对∀y满足Fy≤slGy，U（y）是一分布函数，则有

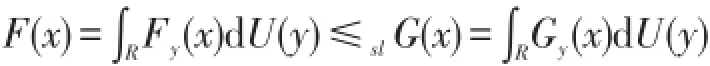
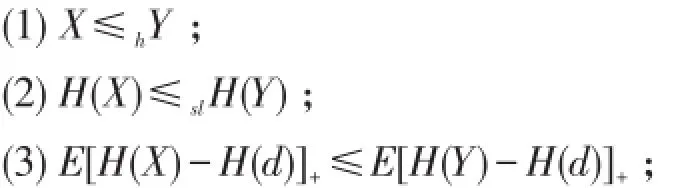
证明 设随机变量X，Y H（X），H（Y）的分布函数分别为F（x），G（x），F1（x），G1（x），显然H（x）在［0，+∞）上递增连续可导，且H（0）=0，H（∞）=∞.

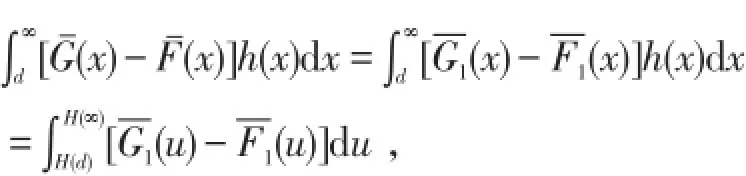
显然d的任意性与H（d）的任意性等价，因此

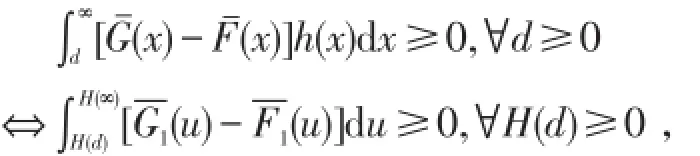
即（1）⇔（2）；

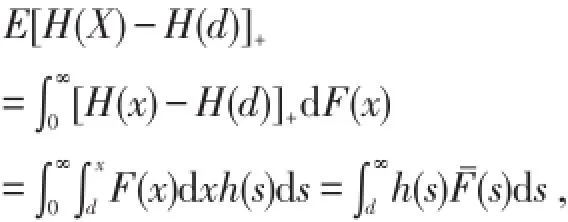
同理可得

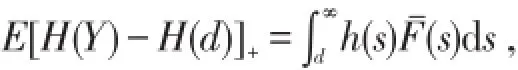
即（1）⇔（3），结论得证.

定理7若E［H（X）］≤E［H（Y）］＜∞且存在某个x0≥0，当 x＜x0时，F（x）≤G（x），反之则否，则有X≤hY.

证明 设随机变量X，Y的分布函数分别为F（x），G（x）令 f（x）=h（x）［F（x）-G（x）］，则当 x＜x0时，f（x）≤0，反之则否.

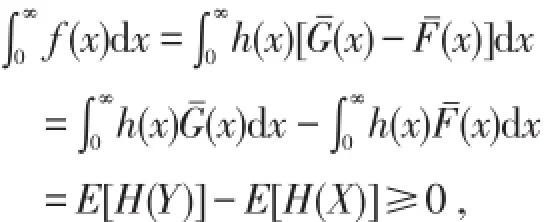
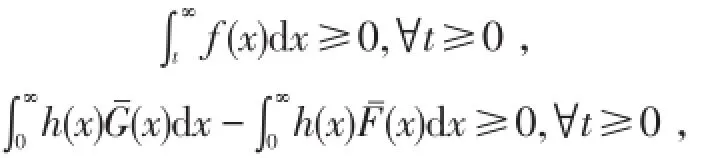
结论成立.

2　停止损失序的判定

在保险精算中，对保险定价等一系列问题的研究都需比较风险大小，由于判断两类风险的大小，只需判断个体理赔额及理赔次数的随机序关系，因此，离散型及连续型随机变量随机序的确定十分重要.

定理8［4］若X，Y是连续型随机变量，X的密度函数为 fX（t），令

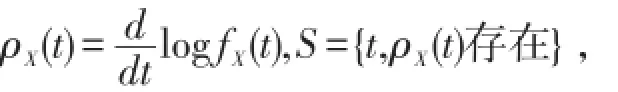
如果EY≤EX且存在常数t0∈S，使得当t∈S⋂（t0，∞）时，ρX（t）≥ρY（t），当 t∈S⋂（0，t0）时 ρX（t）≤ρY（t），则X≥slY.若M，N是离散型随机变量，N的分布列为

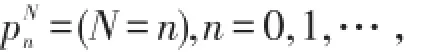
定理9［8］（1）X≤slY⇔对X，Y存在随机变量D使得X+D与Y同分布且E［D|X］≥0；

（2）若FX（x）≤FY（x），x＜C，FX（x）≥FY（x），x≥C，且EX≤EY，则X≤slY.

例1设随机变量X～Pareto（m，σ），m＞0，σ＞1，Y～Γ（α，β），α，β＞0，则

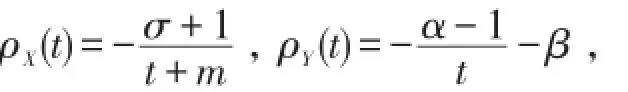
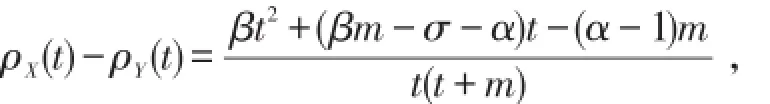
右端分子是关于t的二次函数，设其正根为t0，易知当t＞t0时，ρX（t）≥ρY（t），而0＜t＜t0时，ρX（t）≤ρY（t），由定理8可得X≥slY.

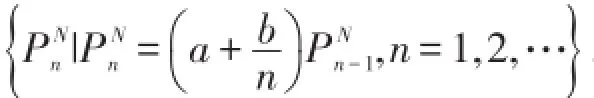
定理10［6］如果随机变量N～NB（r，p），M～P（λ），E［M］≤E［N］，则M≤slN.如果M～B（n，p），上结论也成立.

假设风险集体中理赔次数N～P（λ），参数λ未知且是变量∧的输出值，如果理赔分布的尾概率不是太重情形，例如在机动车险中对自己车辆损伤情况，我们可假定∧～Γ（α，β），则

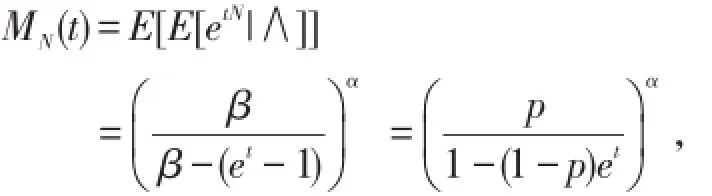
可见

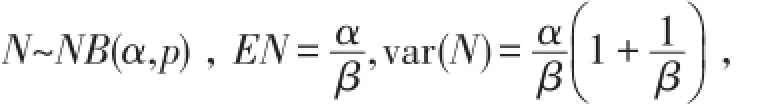
其中α，β的值可通过风险集体的理赔次数统计资料得到估计，由定理8可得泊松分布的伽玛混合

在停止损失意义下大P（α β）.

定理11假设结构变量Λj，j=1，2且给定Λj=λ时，随机变量Nj～P（λ），则Λ1≤slΛ2⇒N1≤slN2.

证明 令fd（λ）=E［（Mλ-d）+］，其中Mλ～P（λ）.

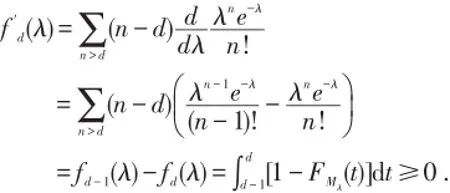
因为当λ＜μ时 Mλ≤stMμ，所以）关于λ单调增，即fd（λ）是单调增凸函数，于是

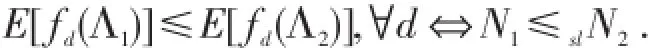
定理12［6］如果

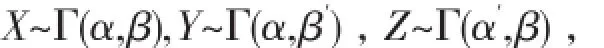
其中 β＞β′，α＜α′，则X≤stY，X≤stZ.

定理13如果Γ（α1，β1）与Γ（α0，β0）均值相等，假定α1＜α0，则方差更大的分布其危险性更高，即较厚的尾.

证明由于

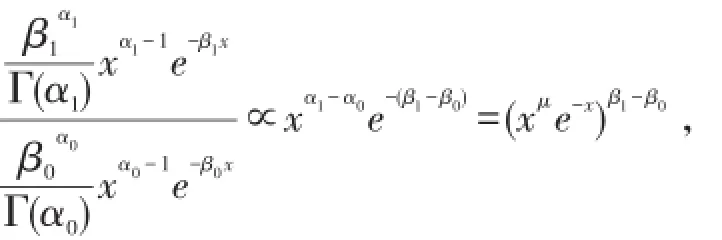
且xμe-x的导函数当0＜x＜μ时为正，而当x＞μ时为负，所以比值（xμe-x）β1-β0穿过任意水平至多两次，因为均值相同，所以两者之间不存在≤st关系，这意味着它们的相交次数必须大于1.因此它们恰好相交两次，这表明其中一个随机变量比另一个随机变量更危险，因为危险性更大的随机变量必是方差较大的一个，所以结论成立.

综上所述可得图1：在（α，β）平面，从（α0，β0）出发沿对角线往原点走，参数对应分布的危险性递增；如果从点（α0，β0）出发，先沿对角线朝原点方向移动到某点，再向右或向下移动到点（α，β），则（α，β）对应分布在停止损失序意义下较大，因为这个分布随机大于危险性高于参数（α0，β0）对应的分布；位于（α0，β0）右下方四分之一区域参数对应的分布随机大于Γ（α0，β0）；位于（α0，β0）左下方八分之一区域参数对应的分布在停止损失序意义下大于Γ（α0，β0），而左下方的对角线之上的八分之一区域所对应的分布，其均值较之Γ（α0，β0）更低，但当d→∞时停止损失保费较之Γ（α0，β0）更高，因为当d=0时，

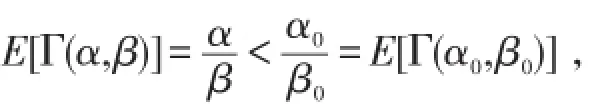
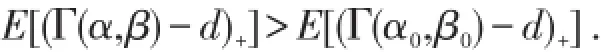
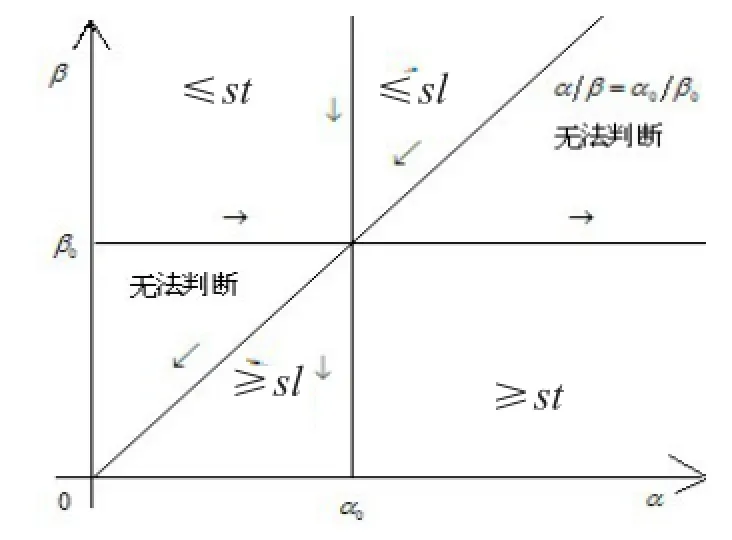
图1　伽玛分布族中的随机序

保险机构极其关心理赔总额S的分布、性质及计算，通常对S作两种假设：［8］

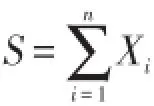
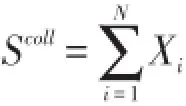
假定

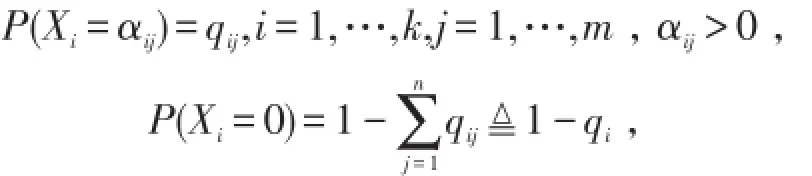
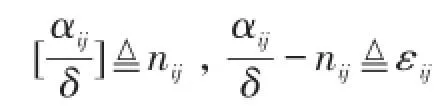
显然有

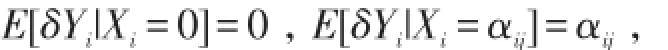
即

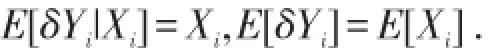
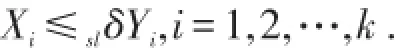
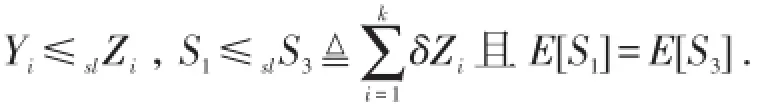
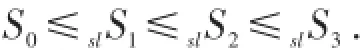
格点化后，概率质量集中，从而方差变大，即风险增加，停止损失序表示所有厌恶风险型决策者的共同偏好，从而也可解释上述结论.

3　停止损失再保险的最优性

停止损失再保险承保保单约定损失超出指定免赔额的超额部分，如果保险事故造成损失为X，则再保险人理赔支付为（X-d）+=max｛X-d，0｝，而原保险人只支付剩余部分.可见，保险人只承担了风险小于d的部分，则其损失一定不会超过d，因此这种形式的保险保障称为停止损失再保险也合情合理，停止损失保费πX（d）=E［（X-d）+］.［9］可以证明：当保险事故损失X≥0时，某再保险合同约定的理赔支付为I（X），假定 0≤I（x）≤x，∀x，则 E［I（X）］=E［（X-d）+］⇒var［X-I（X）］≥var［X-（X-d）+］

对a＞0，令

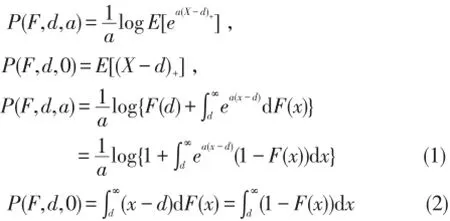
对a≥0，在分布函数族中按如下方式定义一个偏序.若G和H是任意两个分布函数，P（G，t，a）≤P（H，t，a），t∈R，则G≤aH.

由式（1）（2）可得一个等价条件为

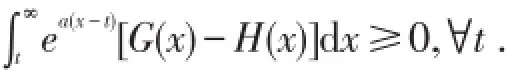
式（1）（2）可以反解，记p（t）=P（F，t，a），则

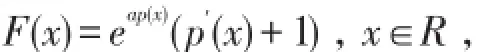
因此在分布函数以及作为免赔额函数的停止损失保费之间有一个一一对应关系.由a=0及上式可得，一个给定的函数p（t），t∈R是一个净停止损失保费当且仅当它满足如下性质：函数p连续，其图形是上凹的，当t→∞时，p（t）→0，当t→-∞时，p′（t）→1；

定理14若对∀分布函数G，H有

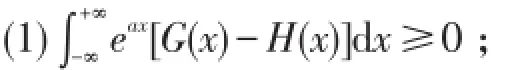
（2）∃β∈R使得

G（x）≤H（x），当x＜β，G（x）≥H（x），当x≥β，则

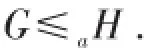
证明 当t≥β时，由条件（2）可得G≤aH；当t＜β时，

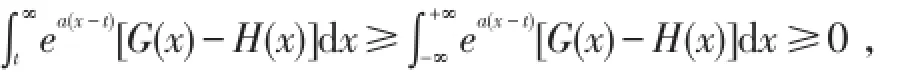
结论成立.

设F是一个分布函数，q表示b，c两点之间的总概率质量，如果把b，c两点之间F的总概率质量由一个点代替，修正后的分布函数记为G.若此点ξ

满足

则定理（14）中条件（1）中的等号成立，条件（2）对β=ξ成立，所以G≤aF.如果把b，c两点之间F的总概率质量由两个端点代替，例如点b的概率质量为q1，c点的概率质量为q2且q1+q2=q，修正后的分布函数记为H.若满足

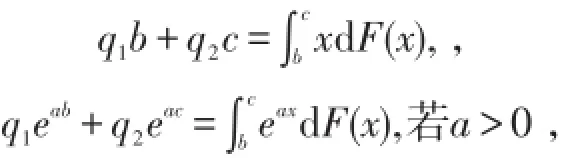
则定理（14）中的条件成立，则F≤aH.

若对某个a＞0有G≤aH，则对∀b＞a有

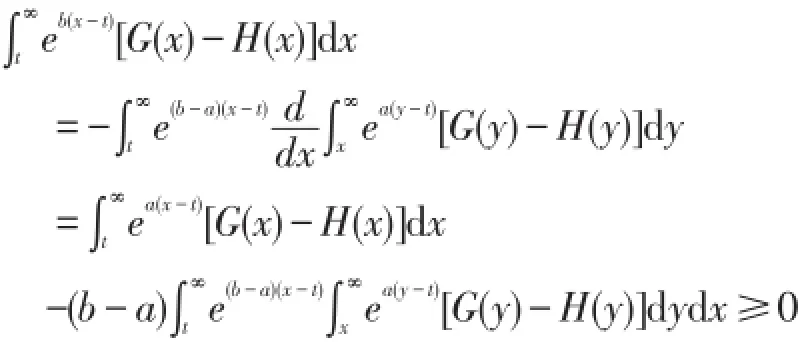
即G≤bH.

显然有

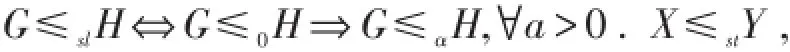
完全等同于使用单调增效用函数的所有决策者对损失风险X和Y的偏好排序.停止损失序表示所有厌恶风险型决策者的共同偏好，该序应用于损失变量，即非负变量.如果两个随机变量有相同的均值，且对于∀d的停止损失保费有一致大小关系.

［1］魏艳华，王丙参.风险交换与停止损失再保险［J］.河北北方学院学报（自然科学版），2011，27（01）：68-70.

［2］胡华.随机序在转换影响问题中的应用［J］.西南民族大学学报（自然科学版），2008，34（4）：381-388.

［3］黄永军，张新生.关于正态分布的次序统计量的随机序［J］.应用概率统计，2009，25（4）：613-618.

［4］王丙参，魏艳华，宋立新.随机序的性质及关系［J］.重庆文理学院学报（自然科学版），2010，29（4）：8-10.

［5］张博.精算学［M］.北京：北京大学出版社，2005：11.

［6］R.卡尔斯，等，著.现代精算风险理论［M］.唐启鹤，等，译.北京：科学出版社，2005：3.

［7］李甜，李余辉.推广的停止损失序及其应用［J］.湖北大学学报（自然科学版），2007，29（1）：10-13.

［8］伍宪彬.保险风险模型的序关系及其误差［J］.数学的实践与认识，2005，35（8）：11-15.

［9］汉斯U.盖伯，著.数学风险论导引［M］.成世学，严颖，译.北京：世界图书出版公司，1997，11：120-158.

〔责任编辑 高忠社〕

O211.9

A

1671-1351（2016）02-0004-05

2016-01-05

王丙参（1984-），男，河南南阳人，天水师范学院数学与统计学院讲师。