基于比例odds模型最小次序统计量的随机比较

张艺馨（天水师范学院 数学与统计学院，甘肃 天水 741001）

基于比例odds模型最小次序统计量的随机比较

张艺馨
（天水师范学院 数学与统计学院，甘肃 天水 741001）

在比例odds模型的框架下，对它的最小次序统计量作了随机比较，包括似然比序，失效率序和随机序.

随机序；反失效率序；似然比序；比例odds模型

1　研究背景和预备知识

近年来，次序统计量倍受国内外学者的关注，它在统计推断、拟合优度检验、可靠性理论及经济学等领域都有重要应用.若有一组随机变量X1，X2，…，Xn，可能服从相同的或不同的分布，则用Xi：n表示第i个次序统计量.很多文章对独立同分布的情形做了研究，【1-3】由于非独立同分布样本的次序统计量比较复杂，所以仅有有限的文章讨论了此种情形.［4-7］

Marshall&Olkin［8］通过生成一个参数扩展了生存函数为（x）的分布族，并且定义这族生存函数为

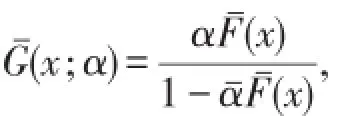
若独立随机变量组X1，X2，…，Xn满足

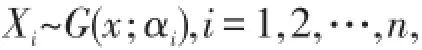
则称这组随机变量属于比例odds模型.这里就比例odds模型最小次序统计量的随机性质进行研究.

定义1设两个随机变量X和Y分别具有密度函数 f和g以及分布函数F和G.令

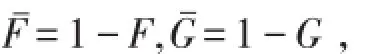
为相应的生存函数，则

（1）若g（x）f（x）关于x单调递增，则称X以似然比序小于Y，记作X≤lrY；

定义1中的随机序有以下包含关系：

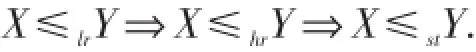
定义2给定两个向量x=（x1，…，xn）∈ℜn和

（3）若向量x与y的每一个分量都严格大于零，且

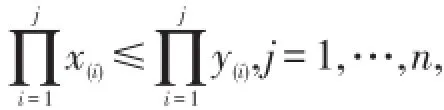
定义2中的序有如下关系：

引理1［10］令I⊂ℜ是一个开区间，并令φ：In→ℜ连续可导.则称φ在In上是Schur-凸［Schur-凹］当且仅当φ在In上对称并对所有i≠j，

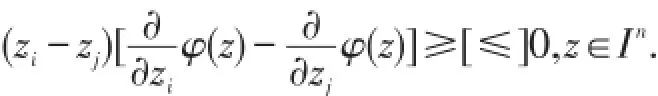
引理2［11］函数满足

当且仅当

2　结果及其证明

定理1设有两组独立非负随机变量X1，…，Xn和Y1，…，Yn，分 别 满 足 Xi～G（x；αi）且Yi～G（x；βi），i=1，…，n，这里αi＞0，βi＞0，i=1，…，n.如果

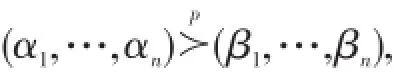
那么，X1：n≤stY1：n.

证明 X1：n的生存函数为

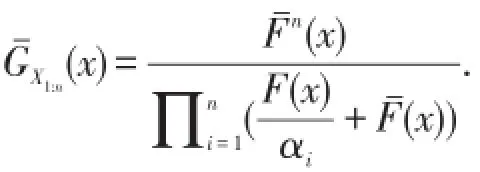
要证明X1：n≤stY1：n.，只需证明

这里ai=logαi，i=1，…，n.此时对任意k，l∈1，…，n，

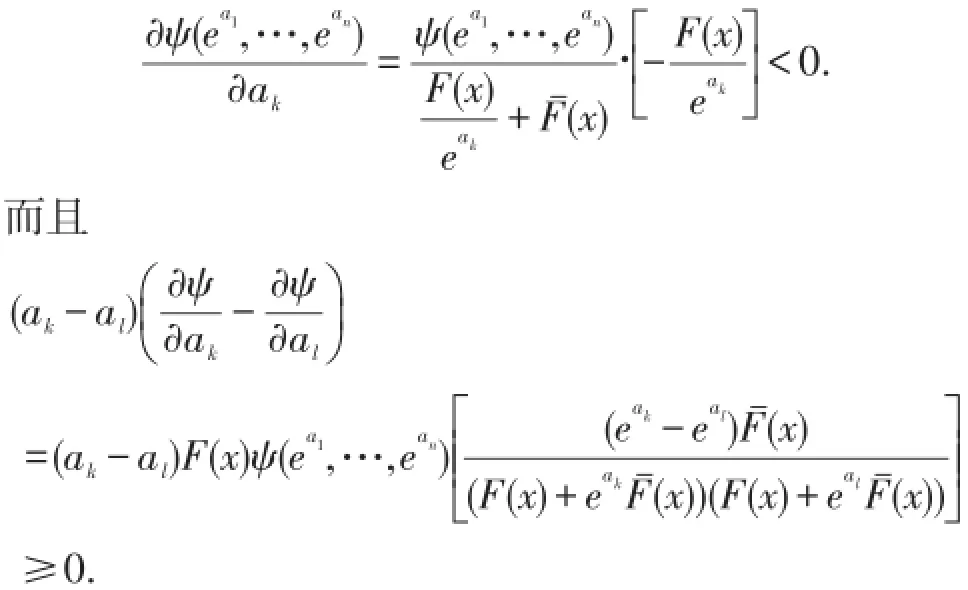
定理2设有两组独立非负随机变量X1，…，Xn和 Y1，…，Yn，并且满足 Xi～G（x；αi）且 Yi～G（x；βi），i=1，…，n，这里αi＞0，βi＞0，i=1，…，n.如果

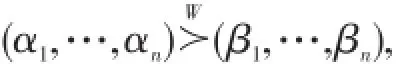
那么，X1：n≤hrY1：n.

证明 X1：n的概率密度函数为

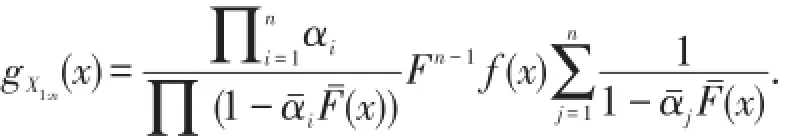
它的失效率函数为

对h（α）求导可得

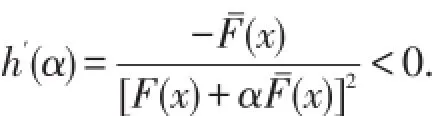
再次求导有

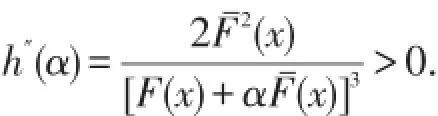
定理3设有两组独立非负随机变量X1，…，Xn和Y1，…，Yn，并且满足 Xi～G（x；αi）且 Yi～G（x；βi），i=1，…，n，这里αi＞0，βi＞0，i=1，…，n.如果

那么，X1：n≤lrY1：n.

证明 X1：n与Y1：n的概率密度函数之比为

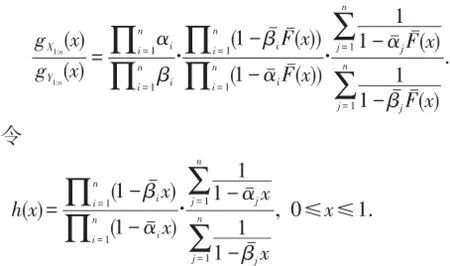
对h（x）求导有

其中

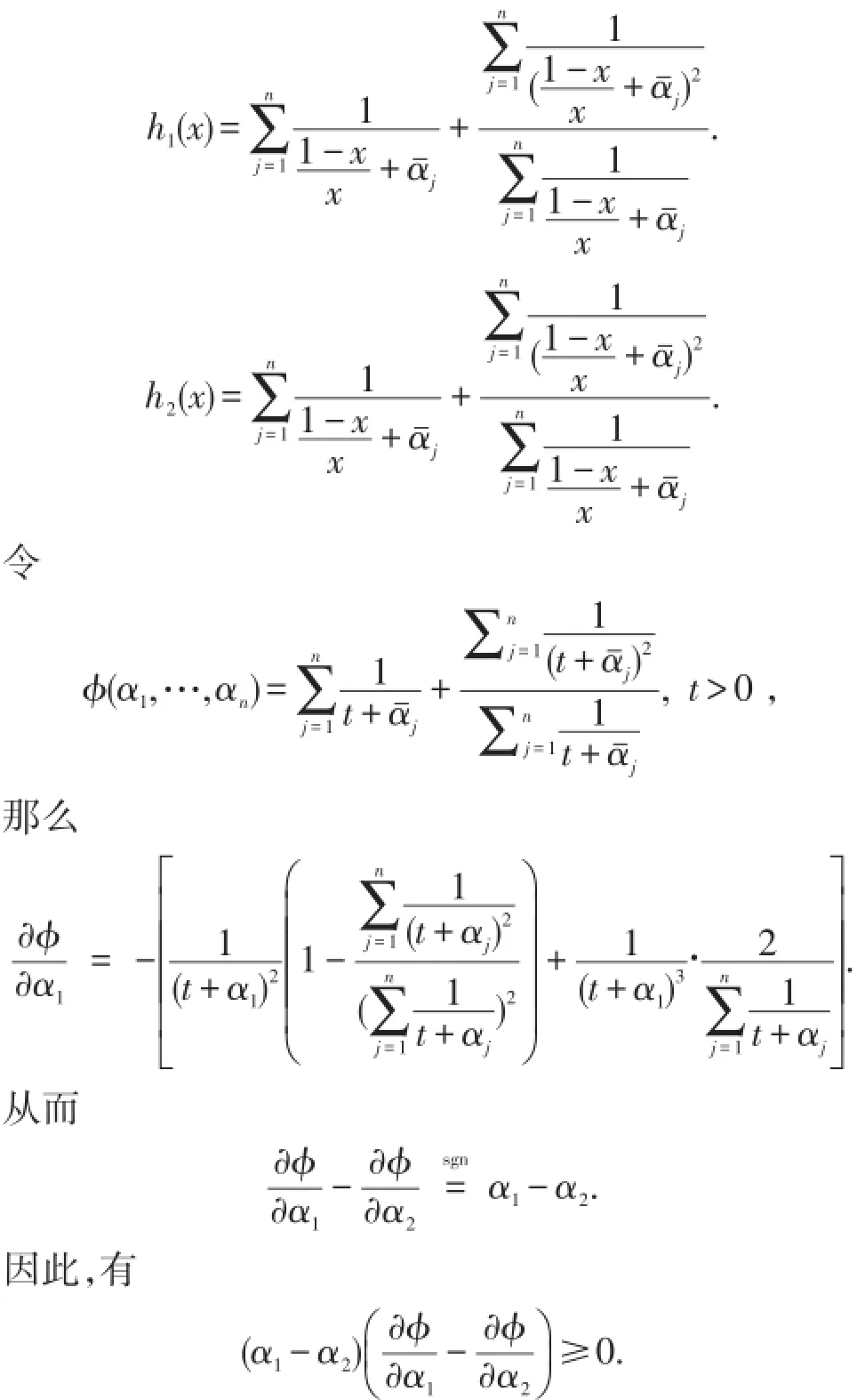
由引理2，可得h1（x）≥h2（x）.所以h（x）关于x递增，结论成立.

3　总　结

通过本论文的研究，对比例odds模型最小次序统计量有了相对完整的随机序比较结果，以后可以对比例odds模型最大次序统计量的随机序进行研究，也可以对基于指数分布的比例odds模型的次序统计量进行研究。

［1］JOO S.，MI J..Some properties of hazard rate functions of sys tems with two components［J］.Journal of Statistical Planning and Inference，2010，140：444-453.

［2］KHALEDI B.E.，KOCHAR S..Some new results on stochastic comparisons of parallel systems［J］.Applied Probability，2000，37：283-291.

［3］PENG ZHAO，BALAKRISHNAN N..Some characterization results for parallel systems with two heterogeneous exponen⁃tial components［J］.Statistics，2011，45：593-604.

［4］Balakrishnan N.，Rao C.R..Order Statistics：Theory and Methods［M］.Amsterdam：Elsevier，1998.

［5］BALAKRISHNAN N.，RAO C.R..Order Statistics：Applications［M］.Amsterdam：Elsevier，1998.

［6］BALAKRISHNAN N..Permanents，Order statistics，Outliers，and Robustness［J］.Maremática Complutense，2007，20：7-107.

［7］DAVID H.A.，NAGARAJA H.N..Order statistics［M］.New Jersey：John Wiley Sons，2003.

［8］MARSHALL A.W.，OLKIN I..A new method for adding a parameter to a family of distributions with application to the ex⁃ponential and Weibull families［J］.Biometrika，1997，84：641-652.

［9］MARSHALL A.W.，OLKIN I..Life Distributions：Structure of Nonparametric，Semiparametric and Parametric Families［M］.New York：Springer.

［10］MARSHALL A.W.，OLKIN I..Inequalities：Theory of Majorization and its Applications［M］.New York：Academic Press，1979.

［11］KHALEDI B.E.，KOCHAR S.C..Dispersive ordering among linear combinations of uniform random variables［J］.Statisti⁃cal and Planning Inference，2002，100：13-21.

〔责任编辑 高忠社〕

O212

A

1671-1351（2016）02-0016-03

2016-01-12

张艺馨（1989-），女，甘肃平凉人，天水师范学院数学与统计学院教师。