平面图绘制算法的研究与实现

王银媛

（武进开放大学， 江苏 常州 213149）

平面图绘制算法的研究与实现

王银媛

（武进开放大学， 江苏 常州 213149）

围绕平面图绘制的“平面图节点绘制顺序和平面图节点坐标确定”两个问题进行研究，重点阐述了平面图节点绘制顺序的两种方法(规范次序法和规范分解法)，并在此基础上研究了画法的具体算法，并对应用性进行了探究。

平面图；规范次序；规范分解；平面图直线画法；平面图凸形画法

平面图绘制算法的研究与实数据可视化技术是当前计算机研究的热点之一，用各种各样的图形表示数据，可以更直观地显示数据的本质。若能通过对平面图绘制算法的研究与开发，并使其应用于可视化技术平台开发，对数据的表示将具有十分重要的应用价值。

图是一种应用非常广泛的数据结构，它可以直观、准确地表示多种复杂的系统模型，其中用图的顶点表示系统中的元素，图的边表示元素之间的关系。将一个图美观、整齐地画到二维或三维空间的一个有限区域中具有重要的理论意义和实际应用价值。图在信息可视化、图形用户接口、软件工程、VLSI布局、电路布线、网络管理等都有广泛的应用。一般可将图结构分为树、平面图、一般无向图、一般有向图。对于各类图的结构已有不少画图算法，平面图绘制算法是其中一类重要的算法，许多学者对此作过较为深入的研究。现有的关于平面图的算法都比较复杂，难以理解。寻找简单，高效的平面图画图算法是一个急需要解决的问题。目前可视化数据挖掘的应用可越来越广泛，也需要各种图形技术的支撑。

平面图是最常用的一种图，也是在图论中最清晰明了的表示方法之一，一个理论上可用平面表示的图，必须要用一定的算法才能将这个图以平面形式画出。

一、平面图绘制的美学标准

根据应用的不同，对平面图的绘制也有不同的要求。但在画平面图时通常要考虑一定的美观度。在绘制平面图时，常用的美学准则如下：

关联于同一顶点的边所构成的最小角最大化；纵横比不要太大或太小；尽可能使边长一致；在所画出的图中，任意两个顶点之间的距离不小于规定的最小值的前提下使图中所有边的长度之和最小；在所画出的图中，任意两个顶点之间的距离不小于规定的最小值的前提下使图的面积最小；反映图的内在对称性。

二、平面图的定义及绘制

（一）平面图的定义

平面图是指一个图能够在两维空间中表示，且画出后，边与边没有交叉[1]。

定义1（平面图）一个图如果能在一个平面上画出，没有边交叉，称为平面图。

定义2（平面图的面）平面图的一个面（face）是以任意拓扑方式用边围绕的连接区域。平面图中一个无界的面称为外部面（outface或exterior face）。所有其它的面称为内部面（interior face）。属于外部面的边称为外部边（exterior edge），属于外部面的节点称为外部节点（exterior node）。连接两个外部节点的边称为弦（chord）。

定义3（平面表示）一个图的平面表示是中节点对平面中点的映射，中的边对Jordan曲线的映射。

定义4（平面嵌入）如果图能画在一个平面上，并且在中除了端点以外。任意两条边都不相交，这样的画法所得的图称为图一个平面嵌入。如果可嵌入平面，称为平面图，否则称为非平面图。

定义5（外平面图）一个图，如果所有点都能以出现在外部面上的方式画出，这个图称为外平面图。

（二）平面图绘制

平面图绘制就是将一个理论上可用平面表示的图，用一定的算法将图以平面形式画出。如图1所示。图1（a）是一个电路的设计图，当制作印刷电路板时需要一个平面图表示，如图1（b）所示。

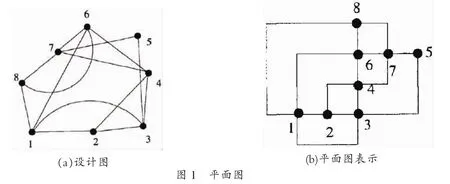
图1平面图

一般来说，平面图表示有三个问题要解决：平面图的平面性问题，平面图节点绘制顺序问题和平面图节点坐标确定问题。平面图的平面性问题不在本文讨论。本文中绘制的图都是可平面的。平面图节点绘制顺序决定了一个平面图是否能正确地画出，常用的方法有规范次序法和规范分解法等方法[2]。

三、基于规范次序的平面图绘制

绘制平面图一般采用节点添加法。所谓节点添加法就是在平面图绘制过程中，逐个增加图的节点及相关的连接边，直至添加完全部节点，将平面图绘制完成。然而，在节点添加法中，节点添加的次序是至关重要的。如果随意添加节点，很可能不能得到图的平面绘制，规范次序就是一种节点添加的次序，下面主要讨论三角图的绘制方法。

（一）规范次序定义

令G是一个画在平面上的极大平面图，令u,v,w是其外部面上的边界。规范次序是对图G节点v1，v2，…，vn的一个标注，也是一种排序，使得v1=u1,v2=v且vn=w。并对3≤k≤n，以下条件成立：

由节点v1，v2，…，vk-1导出的G的子图Gk-1是二连通的，且其外部面的边界是一个环Gk-1，包含边(u,v)；

节点vk在Gk-1的外部面上，在Gk-1中至少有两个邻接节点。并且，vk在Gk-1上的所有邻接节点在路径Gk-1-(u,v)上是连续的[3]。

规范次序的说明见图2。图是一个极大平面图，实际上，它也是一个三角图。节点，有时称为一个平面图的底边。根据规范次序绘制平面图的基本思想是首先取规范次序中前两个节点作为平面图的底边，然后添加节点，并添加其连接边，构成一个三角形。在此基础上，逐个添加节点及其连接边，直至将图中的所有节点都添加到画面上，完成整个平面图的绘制。在整个平面图的绘制过程中，需要不断调整图中节点的坐标，使其不出现边的交叉和重叠，保持其平面性。

图2 规范次序的说明

规范次序并不确定节点的坐标，它只是保证以这样的次序添加节点，在绘制过程中能保证平面图的平面性[4]。

（二）规范次序算法

规范次序是在绘制平面图时，逐个增加节点的次序。在选择加入规范次序的节点时，需要考虑候选节点与当前子图外部面上环的节点之间的邻接关系[5]。

用反向推理，假定在图中，已经适当地选择了节点vn，vn-1，…，vk+1（k+1≥4），使得对于满足规范次序的条件。如果在环上能选择一个节点作为，不是上一根弦的端点，如图2.1所示。那么，因为，显然，满足规范次序的条件。因此，存在一个节点满足规范次序的条件。令环Ck=w1，w2，…，，wt，其中w1=v1，wt=v2。如果Ck没有弦，那么节点w2，w3,…，wt-1中的任意节点就是这样的节点w。

图2.1 规范次序算法的候选节点（1）

假定Ck有弦，那么Gk有一个“最小的弦”（wp，wq）(p+2≥q)，使得没有一个节点是这根弦的端点，如图2.2所示（弦用粗线画出），那么。节点中的任意节点都可以作为候选节点。

图2.2 规范次序算法的候选节点（2）

由上述分析，我们已得到了构造规范次序节点表的方法。先取3个相邻接的节点，这3个节点能构成一个三角形。设这3个节点能构成一个三角形。设这3个节点为v1,v2,vn，以此为基础，计算规范次序节点表中节点的规范次序。

因此，计算三角图规范次序算法的数据结构如下：

给定三角图G=(V,E)。对各个节点v∈V，分配下列属性：

v.mark，如果v已增加到次序表中为true，否则为falss；

v.out，如果v是当前平面图的外部节点为true，否则为flase；

v.chords，端点为v的外部环的弦个数。

用c表示子图Gk-1外部面的环Ck-1。

四、基于规范分解的平面图绘制

当一个平面图不是三角图时，规范次序的要求将更加严格。在三角图中，规范次序要求vk+1在路径Ck-(v1，v2)（轮廓）上有连续的邻接节点。然而，考虑图3.1，G3的外部面是v1，v2，y在这种情况中，如果规范次序指定v4=x，x的邻接节点在C3=v1，y,v2上不形成连续的片段。因为y不是x的邻接节点[6]。

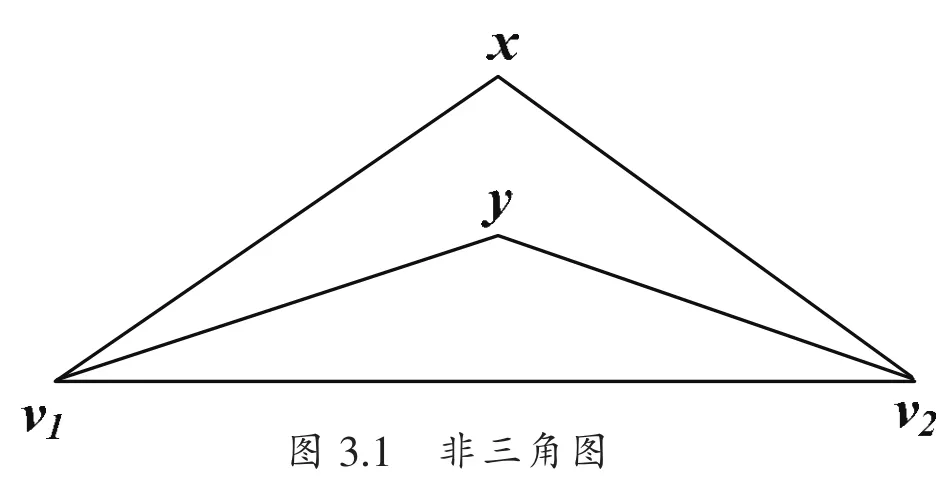
图3.1 非三角图

再如图3.2，添加节点时，不能构成外部面的环，按上一章的方法，也无法进行平面图的绘制。

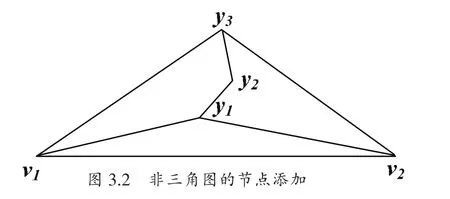
图3.2 非三角图的节点添加

这是因为图3.1和图3.2中的图不是三角图，需要我们对节点添加次序有一个新的定义，使我们在绘制图时，能顺利地添加图中所有节点。通过节点添加次序的另一种方法：规范分解法，可以将平面图的节点进行划分，划分为单个节点或多个节点的子集。在绘制平面图时，按照划分的节点集合进行节点添加。

（一）连通图的规范分解

如果图G=(V，E)存在两个节点x和y，这两个节点能把图G分离为两个图G1和G2，称这一对节点{x,y}为一个分离对。G1和G2称为分离图[7]。

如图3.3所示，将G1定义为由获得的分离图，在G1中，如果没有边(x,y)，增加边(x,y)；将G2定义为由获得的分离图，在G2中，如果没有边{x,y}，增加边{x,y}。

图3.3 分离对和分离图

图3.4 不是内部3-连通的2-连通平面图

如果平面图是2-连通的，对图的任意分离对，和是外部节点，并与包含一个外部节点的相连接，这个平面图称为是内部3-连通的。

换言之，如果图是内部3-连通的，当且仅当在外部面上增加一个节点能够扩展为一个3-连通图，增加的节点与所有外部节点连接。如果一个2-连通图不是内部3-连通的，那么图中有如图3.4中所示三种类型的分离对之一。在图3.4中，分离部分包含一个不是或的外部节点。

如果一个内部3-连通的平面图不是3-连通的，那么图有一个外部节点的分离对，当图不是一个单独的环时，有一个“弦路径”。

（二）规范分解算法

在算法中主要是维持一个数据结构，在构造时，这个数据结构保持了的外部链和最小弦路径。下面描述算法的轮廓[8]。

令Gl=G，Gl-1=G-{vn}=G-Ul。在图G中先找一个度数大于或等于3的节点vn，作为单个节点集合Ul。令Gl-1=Gk，Gl-2=Gk-1，Gk-Uk=Gk-1。算法从G1=Gk开始，找到规范划分中的子集Uk，Uk-1,直到找到U1。

从Gl=G起，每找到一个划分的子集Uk时，将其从当前节点集合Vk删除，加入中，得到从Vk-1导出的子图Gk-1。显然，与邻接的节点都在子图Gk-1的外部面上。令w1，w2，…，wt是子图Gk-1的外部节点，以顺时针顺序出现在Ck-1上，其中w1=vt和wt=v2。

如果Gk-1是3-连通的。设节点w是Gk-1中的邻接节点，利用规范分解中的条件（CD3），如果w在Gk-1上是3-连通的，即内部3-连通的，Uk-1是单个节点集合{w}。

如果Gk-1是内部3-连通的，且不是3-连通的。则对Ck-1有一个弦路径。令p是一个对Ck-1的最小弦路径，令wp和wq是p的两个端点（p＜q），因为Gk-1是内部3-连通的，{wp，wq}是Gk-1的一个分离对，那么q≥p+2。{wp+1，wq+2，…，wq-1}是Gk-1的一个外部链。选择{wp+1，wq+2，…，wq-1}作为Uk-1。因为Uk-1是一个外部链，p是一个最小弦路径，可知Uk-1∩U1≠Ø。因为G是3-连通的，各个节点w∈Uk-1在Gk-1中度数为2，各个节点w∈Uk-1在中有一个邻居。实现时，在Gk-1上找内部2-连通的节点w，然后在Gk-1的外部面上找w的邻接节点，如u，如果u在Gk-1上是内部2-连通的，扩展集合Uk-1，此时Uk-1是Gk-1上的一个外部链，如此，直到外部链不能再扩展，得到集合Uk-1。

算法的终止条件是，所剩节点都是内部2-连通的，得到U1。因为在构造划分子集Uk时，不断在原节点集合V上删除节点，加入到中，至多在只有3个节点时，构成一个三角形，此时，这3个节点都是2-连通的，得到U1，算法得以终止。如果多于3个节点，这些节点都是2-连通的，形成一个环，得到U1，算法得以终止。所以算法一定是可终止的。

规范分解算法的数据结构：

规范划分表：，U1,…，U2，U1,其中Ui,为该划分的节点集合，各个Ui用一个数组表示；

在图G的节点邻接矩阵中，开始时邻接边用1表示，在划分过程中，与中节点邻接的边用-1表示。

五、平面图绘制在平台上的实现

因考虑到目前的应用基本上都是使用B/S方式，因此使用了WPF技术，开发平台选用Microsoft的.NET平台。WPF是基于技术.NET的新一代开发平台，实现了桌面应用程序和互联网应用程序的统一编程，实现了数据驱动用户界面，编程语言采用C#语言。

在数据分析部分，按照数据实体和实体之间的关系确定图的节点和边，构造数据实体关系表。在数据实体关系表中，有数据实体的各种属性，与应用密切相关。在图形表示程序中，只需要数据实体的关系，因此，利用数据实体关系表中的关系信息，构造一个图结构，即用图中的节点表示现实世界的实体，用图的边表示实体之间的关系。图结构由两部分组成：源节点表和节点邻接矩阵。源节点表包括与数据实体关系表对应的节点序号，以及显示的标注信息。节点邻接矩阵用图的关联边表示实体之间的关系，这样就能做到数据与表示方法分离，可以独立研究数据的表示问题。在可视化部分，输入为源节点表和节点邻接矩阵，通过选择适当的算法，将数据关系用图的方式进行显示。

计算机技术和开发环境的日益提高，人们对图形化的界面技术要求也越来越高，平面图的应用非常广泛，因此一定要有良好的平面图表示技术。通过将平面图绘制技术用于数据可视化，并与数据平台相结合，进行数据组织与分析，对满足各种应用的需求潜力巨大。

[1]翟金刚,张教军.基于极大平面图矩形图元布局问题的全局优化算法 [J].鲁东大学学报 (自然科学版)，2010,26(4): 293-296.

[2]Kumar P.Graph Visualization and its Applications[D].Ph.D.thesis,The UniversityofTexas,2009.

[3]SHEN Z.Visual Analysis ofComplex Social Networks[D].Ph.D.thesis,Dept.of Computer Science,University of California, 2009.

[4]Healy P,Nikolov N S.Applications of Parameterized st-Orientations in Graph Drawing Algorithms[J].Graph Drawing, Lecture Notes in Computer Science,2006,Volume 3843/2006, 355-367.

[5]王晓白，王 欢,等.UML类图层次化自动布图算法[J].软件学报，2009，20（6）：1497-1498.

[6]张军英，覃 强，等.平面化问题的一种新型神经网络算法[J].中国科学E辑:信息科学，2008，38（12）：2163-2172.

[7]刘缵武.应用图论[M].国防科技大学出版社，2006.

[8]赵长虹.超大规模集成电路的平面布图规划算法研究[D].复旦大学博士学位论文，2006.

（责任编辑：魏树峰）

Research and Implementation of Planar Graph Drawing Algorithm

WANG Yin-yuan
（Wujin Open University,Changzhou 213149,China）

The node drawingsequence and nodal coordinates ofplanar graph drawingare studied.The twomethods of node drawingsequence,i.e.canonical sequence and canonical decomposition,are presented.Based on the above study,the specific algorithmofdrawingis illustrated and its applications are addressed.

planar graph;canonical sequence,canonical decomposition,straight line drawing;convexdrawing

TP311.11

A

2016－10－03

王银媛（1980-），女，江苏常州人，讲师，研究方向：计算机程序设计与开发、计算机软件应用。E-mail:meidxidowx@126.com．

1671－802X(2016)06－0028－05