超越整函数复合函数Fatou分支的有界性

杨存基，王少敏

（大理大学数学与计算机学院，云南大理 671003）

超越整函数复合函数Fatou分支的有界性

杨存基，王少敏

（大理大学数学与计算机学院，云南大理 671003）

证明了超越整函数复合函数动力系统Fatou分支有界性的几个结果，给出了其Fatou分支有界的几种充分条件，改进和推广了前人相关的结果。

复动力系统；超越整函数；Fatou分支；有界性

设 f为超越整函数，记 f1=f，当n≥2时，fn=f∘fn-1为函数 f的n次迭代。函数族{fn(z)}的正规点形成的集合称为函数 f的Fatou集，记为F(f)，而J(f)=CF(f)称为函数 f的Julia集。有关函数迭代和复解析动力系统的基本理论参见文献〔1-8〕。

1981年，Baker在文献〔9〕中证明了：对于充分大的正数a，函数

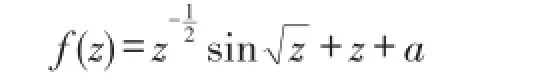
1 主要引理

我们先给出证明本文主要定理所需的一些引理。函数 f的最大模M（r，f）、最小模m（r，f）、增长级ρ和下级μ分别定义如下：

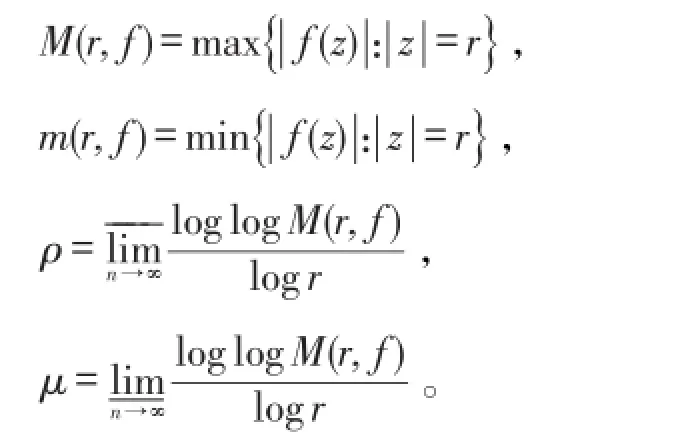
为了方便，有时将函数 f的最大模M（r，f）和最小模m（r，f）分别记为M（r）和m（r）。

引理1（〔17〕，引理2.2） 设 f为超越整函数，则存在正数R＞0使得对所有r＞R和c＞1，logM(rc,f)≥c∙logM(r,f)。

引理4（〔11〕，引理3） 设h(z)=fN∘fN-1∘…∘f1(z)，其中(j=1,2,…,N)为级的超越整函数。则存在常数σ＞1,r0＞0，当r≥r0时，环{z|r≤|z|≤rσ}中有一条围绕原点的简单闭曲线Γ，在Γ上，| h(z)|= M(r,h)。

当N=1时，由引理4得下列结果。

引理6 设h(z)=fN∘fN-1∘…∘f1(z)，其中 fj(j= 1,2,…,N)为级的超越整函数。则存在常数σ＞1,r0＞0，当r≥r0时，存在正数t满足r≤t≤rσ且m(t,h)=M(r,h)。

证明：由引理4，存在常数σ＞1,r0＞0，当r≥r0时，存在围绕原点的简单闭曲线Γ1⊂{z|r≤|z|≤rσ}使得对所有z∈Γ1,| h(z)|=M(r,h)。类似的，存在绕原点的简单闭曲线Γ2⊂{z |rσ≤|z|≤rσ2}使得对所有z∈Γ2，| h(z)|=M(rσ,h)。

当N=1时，由引理6可推出引理2。由引理6，有下列结果。

引理7 设h(z)=fN∘fN-1∘…∘f1(z)，其中 fj(j= 1,2,…,N)为级的超越整函数。设σ为充分大的常数。假若存在一个由Rn+1=M(Rn,h)定义的趋向于无穷的数列Rn和实函数ψ：[R1,∞)↦[R1,∞)，使得当 n∈Ν时 ψ(r)≥r且 M(ψ(r),h)≥ψ(M(r,h))σ。则存在数列 ρn使得：（1）Rn≤ψ(Rn)≤ρn≤(ψ(Rn))σ，（2）m(ρn,h)≥(ψ(Rn+1))σ。

引理8（〔10〕，引理2.7） 设 f为超越整函数且存在趋于无穷序列 Rn，ρn和 c(n)＞1使得（1） Rn+1=M(Rn,f)，（2）Rn≤ρn≤(Rn)c(n)，（3）对充分大的n，m(ρn,f)≥(Rn+1)c(n+1)。则F(f)的每个分支都有界。

2 主要结果

定理1 设h(z)=fN∘fN-1∘…∘f1(z)，其中 fj(j= 1,2,…,N)为级的超越整函数，如果h(z)的下级大于0，则F(h)的每个分支都有界。

给定正数R(1)＞r0，归纳定义：

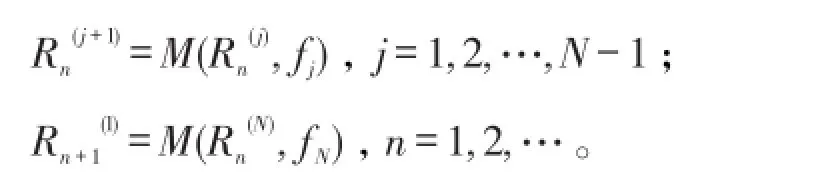
当n∈Ν时，由上述定义及函数h(z)和 fN的超越性知。所以，当n趋于无穷时，，且对所有 j=1,2,…,N，当n趋于无穷时。设

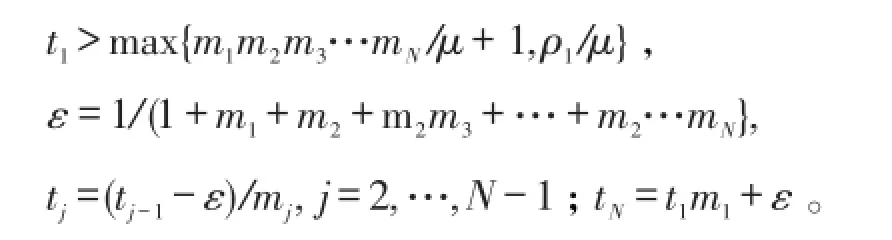
给定充分大的正整数n0，由引理2，当n≥n0时，存在使得

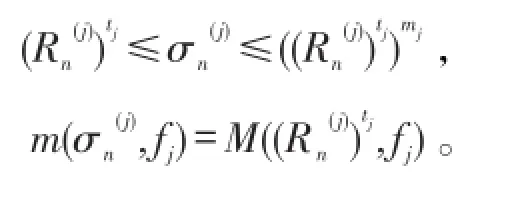
对j=1,2,…,N-1，由定理1的条件、引理2和引理1得：

假设F(h)有无界分支D。不妨设0，1属于J(h)，则在D内，每个映射hn(z)都没取到0，1。由D的无界性和连通性知存在正整数n1≥n0使得，对所有n≥n1，D与下列圆相交

其中 j=1,2,…,N-1。挑选适当的正整数k满足k≥n1，则D内必包含连接从点 ωk(1)∈αk

(1)到点曲线Γ。由上述圆的位置关系知曲线Γ包含了两条子曲线Γ′、Γ″，其中Γ′连接到且包含了；Γ″连接到。由 于，因 此 ，|。又由上述证明知

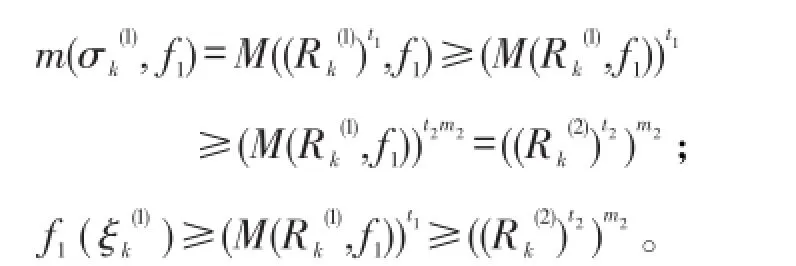
重复上述过程，我们得到h(Γ′)=fN∘fn-1∘…∘包含连接从点到点的一段弧；h(Γ″)=fN∘fn-1∘…∘f1(Γ″)包含连接从点到点的一段弧。由于Γ′和Γ″是Γ的两条子弧，因此，h(Γ)必包含连接从点到点的一段弧。由归纳法知：hn(Γ)包含连接从点到点的一段弧。所以，hn(D)是F(h)的包含hn(Γ)的分支，并且在Γ上，hn(z)取得模至少为的值，且当n趋于无穷时，。所以，在D内局部一致收敛到无穷。因此，存在正整数N使得对所有n＞N和z∈Γ都有| hn(z)|＞1。所以函数族{hn(z)}n＞N在Γ上满足引理3的条件，从而存在常数A，B使得对所有n＞N和都有。当 n＞N时，挑选使得 hn(zn)=和，则对所有n＞N，

注1 定理1是文献〔16〕中的定理的改进。进一步取N等于1，由定理1，我们得到如下的推论。

类似定理1的上述证明方法，可证明下面定理。

定理2 设h(z)=fN∘fN-1∘…∘f1(z)，其中 fj(j= 1,2,…,N)为级的超越整函数，设σ为充分大的常数。如果存在正数r0＞1，使得对所有r＞r0和任意小的正数ε，M(rσ,h)≥M(r,h)σ+ε。则F(h)的分支都有界。

注2 定理2是作者在文献〔13〕中得到的主要结果的推广，将单个超越函数的结果推广到有限个超越函数的复合函数。

定理3 设h(z)=fN∘fN-1∘…∘f1(z)，其中 fj(j= 1,2,…,N)为级的超越整函数，设σ为充分大的常数，r0为正常数。如果存在定义在(r0,∞)上的实函数 ψ使得，当r≥r0时，ψ(r)≥r且 M(ψ(r),h)≥ψ(M(r,h))σ。则F(h)的分支都有界。

证明：由定理3的假设条件，存在定义在(r0,∞)上的实函数ψ使得对r≥r0，ψ(r)≥r且M(ψ(r),h)≥ψ(M(r,h))σ，则引理7的条件成立。由引理7存在序列ρn使得

取(ψ(Rn))σ=Rnc(n),其中c(n)＞1，则

由引理8，F(h)的分支都有界。

注3 推论2是Rippon和Stallard在文献〔17〕中证明的定理5的改进。

2010年，在文献〔19〕中，Sixsmith证明了一个类似的结果，见文献〔19〕中定理7.1。在文献〔19〕中推论 7.2，Sixsmith证明了如果 h(z)= fN∘fN-1∘…∘f1，其中 fj(j=1,2,…,N)为级的超越整函数，并且至少一个函数满足对数正则，则F(h)分支有界。

定理4 设h(z)=fN∘fN-1∘…∘f1(z)，其中 fj(j= 1,2,…,N)为超越整函数。设 Rj1＞0 使得由Rjn+1=M(Rjn,fj)定义的序列Rjn→∞。假如存在常数列Lj＞1和正数列ajn使得对所有rj∈[Rjn,Rjn+1)都存在满足

则F(h)的分支都有界。

对所有 r∈[Rn,Rn+1)都存在 t∈(r,rLN)、、′使得和，并且满足，其中。由引理9，F(h)的分支都有界。

如果N=1，由定理4，可得到Hinkkanen在文献〔20〕中证明的定理1。

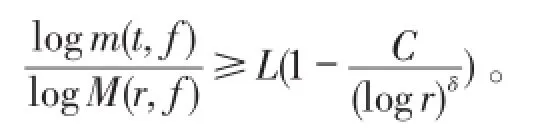
则F(f)的分支都有界。

〔1〕FATOU P.Sur les équations fonctionnelles〔J〕.Bull Soc Math France，1919，47：167-271.

〔2〕FATOU P.Sur les équations fonctionnelles〔J〕.Bull Soc Math France，1920，48：33-94.

〔3〕FATOU P.Sur l'itération des fonctions transcendentsentiéres〔J〕.Acta Math，1926，47：337-370.

〔4〕JULIA G.Mémoire sur l'itération des fonctions rationnelles〔J〕.J Math Pures Appl，1918，8：47-245.

〔5〕BEARDON A F.Iteration of Rational Functions〔M〕.New York∕Berlin：Springer-Verlag，1991.

〔6〕CARLESON L，GAMELIN T W.Complex Dynamics〔M〕. New York∕Berlin：Springer-Verlag，1993.

〔7〕MILNOR J.Dynamics in One Complex Variable，Introductory Lectures〔M〕.Berlin：Vieweg，2000.

〔8〕REN F Y.Complex Analysis Dynamics（in Chinese）〔M〕. Shanghai：Fudan University Press，1996.

〔9〕BAKER I N.The iteration of polynomials and transcendental entire functions〔J〕.J Austral Math Soc（series A），1981，30：483-495.

〔10〕STALLARD G M.The iteration of entire functions of small growth〔J〕.Math Proc Camb Phil Soc，1993，114：43-55.

〔11〕QIAO J Y.Stable set for iteration of entire functions（in Chinese）〔J〕.Acta Math Scientia，1993，37：702-708.

〔12〕WANG Y F.Bounded domains of the Fatou set of an entire functions〔J〕.Israel J Math，2001，121：55-60.

〔13〕YANG C J，LI Y H.Bounded Fatou components of transcendental entire functions with order less than 1∕2〔J〕. Acta Math Scientia，2015，31：647-658.

〔14〕YANG C J，WANG S M.Bounded Fatou components of composite transcendental entire functions with gaps〔EB∕OL〕.〔2016-01-01〕.http：∕∕dx.doi.org∕10.1155∕2015∕149182.

〔15〕ZHENG J H，WANG S.Boundness of components of Fatou sets of entire and meromorphic functions〔J〕.Indian J Pure Appl Math，2004，35（10）：1137-1148.

〔16〕CAO C L，WANG Y F.Boundedness of Fatou components of holomorphic maps〔J〕.J Dynam Diff Equa，2004，16：377-384.

〔17〕RIPPON P J，STALLARD G M.Functions of small growth with no unbounded Fatou components〔J〕.Journal d'Analyse Mathematique，2009，108：61-86.

〔18〕BAKER I N.Zusammensetzungen ganer Funktionen〔J〕. Math Z，1958，69：126-153.

〔19〕SIXSMITH D J.Entire functions for which the escaping set is a spider's web〔J〕.Math Proc Camb Phil Soc，2011，151（3）：551-571.

〔20〕HINKKANEN A.Entire functions with no unbounded Fatou components〔M〕∕∕Complex analysis and dynamical systems II，Contemp Math.Amer Math Soc，Providence，RI，2005：217-226.

Boundedness of Compound Function Fatou Component of Transcendental Entire Function

Yang Cunji,Wang Shaomin
（College of Mathematics and Computer Science,Dali University,Dali,Yunnan 671003,China）

This paper proves the results of the boundedness of compound function complex dynamic system Fatou component of transcendental entire functions,provides some sufficient conditions of the boundedness of Fatou component,and improves the previous research results.

complex dynamic system;transcendental entire function;fatou component;boundedness

O174.5

A

2096-2266（2016）12-0001-05

10.3969∕j.issn.2096-2266.2016.12.001

（责任编辑 袁 霞）

国家自然科学基金资助项目（11261002）；云南省教育厅科学研究基金重点项目（2012Z121）

2016-09-27

2016-10-21

杨存基，教授，主要从事复分析、值分布和复解析动力系统研究.