一类广义Emden-Fowler阻尼方程的振动结果
吴波
(普洱学院数学与统计学院,云南普洱 665000)
一类广义Emden-Fowler阻尼方程的振动结果
吴波
(普洱学院数学与统计学院,云南普洱 665000)
利用广义黎卡提变换和积分平均技巧给出了一类广义Emden-Fowler阻尼方程的振动准则,建立了保证此类方程一切解振动或者收敛到零的若干新的充分条件。
广义Emden-Fowler阻尼方程;广义黎卡提变换;振动准则
本文考虑一类广义Emden-Fowler阻尼方程
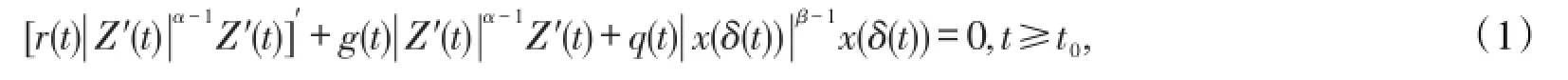

方程(1)的一个非平凡解称为振动的,如果它有任意大的零点,否则为非振动的,如果方程(1)的一切解都是振动则称该方程是振动的。
如果p(t)≡0,g(t)≡0,r(t)≡1,α=1,δ(t)=t,广义Emden-Fowler阻尼方程(1)为经典的Emden-Fowler方程

如果p(t)≡0,r(t)≡1,α=1,δ(t)=t,广义Emden-Fowler阻尼方程(1)为经典的Emden-Fowler阻尼方程

许多学者对方程(2)~(3)的振动和非振动性质做了一些研究〔1-3〕。1983年,Philos〔1〕建立了方程(2)的一些振动准则;1989年,Philos〔2〕进一步推广和改进了文献〔1〕的结论;1986年,Yan〔3〕建立了方程(3)的一些振动准则。
如果 p(t)≡0,g(t)≡0,α=β,广义Emden-Fowler阻尼方程(1)为下列方程

如果 g(t)≡0,广义Emden-Fowler阻尼方程(1)为广义的Emden-Fowler方程:

许多学者对方程(4)的振动和非振动性质做了一些研究〔4-7〕。最近,文献〔7-10〕对下面的方程

做了振动和非振动性质的一些研究。但是这些结果不可以应用于广义的Emden-Fowler方程(5)。
目前,对广义的Emden-Fowler方程(5)振动准则的研究还比较少。2012年,Liu〔11〕利用黎卡提不等式给出了广义的Emden-Fowler方程(5)的振动准则。对广义的Emden-Fowler阻尼方程(1)的振动准则还没有做过研究。本文利用广义黎卡提变换构造了广义黎卡提不等式,进而建立了广义的Emden-Fowler阻尼方程(1)的振动准则,并且这些振动准则都可以应用于广义的Emden-Fowler方程(5)。
1 几个引理
引理1 设x(t)是广义的Emden-Fowler阻尼方程(1)的正解,则相应的Z(t)只有下面的两种情况
证明:设x(t)是广义的Emden-Fowler阻尼方程(1)的正解,由Z(t)的表达式得到Z(t)≥x(t)>0。由方程的第一种情况,得到两种可能:Z′(t)>0或Z′(t)<0。


对上式从t1到t积分,可以得到

让t→∞,利用(H3),得到Z(t)→-∞,这矛盾于Z(t)>0。
本文下面的引理和定理都是基于情形(I)下得到的。
引理2 设x(t)是广义的Emden-Fowler阻尼方程(1)的正解,则

其中,Q(t)=[q(t)(1-p(δ(t)))]β。
证明:由Z(t)=x(t)+p(t)x(ι(t)),可以得到x(t)=Z(t)-p(t)x(ι(t)),利用(H4)和Z′(t)>0,可以得到

利用方程(1),可以得到
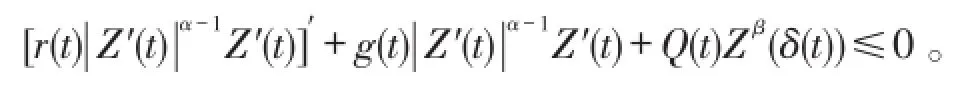
引理3 设x(t)是广义的Emden-Fowler阻尼方程(1)的正解,如果

证明:假设存在两个常数0<M≤N,使得 0<M≤Z(t)≤N,对方程(7)从t到∞积分,可以得到:




则

其中:
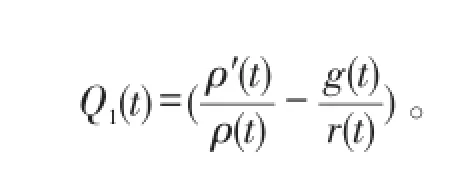
证明:由ϖ(t)的定义可以得到

利用方程(7),可以得到

利用β≥α,H5和引理1,可以得到

由方程(10)~(12),可以得到

2 主要结果
定理1 假设某些条件成立。设x(t)是广义的Emden-Fowler阻尼方程(1)的解,如果

则x(t)振动。
证明:假设x(t)是方程(1)的非振动解,不妨设x(t)是广义的Emden-Fowler阻尼方程(1)的最终正解(对于x(t)是广义的Emden-Fowler阻尼方程(1)的最终负解也有类似的结论),利用引理5可得

利用引理4得到

对上面方程从t0到t积分可得
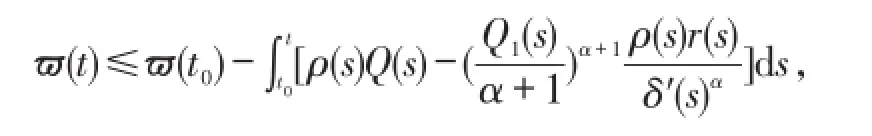
让t→∞,可得ϖ(t)→-∞,这矛盾于ϖ(t)>0。
定理2 假设某些条件成立。设x(t)是广义的Emden-Fowler阻尼方程(1)的解,如果

则x(t)振动。
证明:假设x(t)是方程(1)的非振动解,不妨设x(t)是广义的Emden-Fowler阻尼方程(2)的最终正解(对于x(t)是广义的Emden-Fowler阻尼方程(1)的最终负解也有类似的结论),利用引理5可得
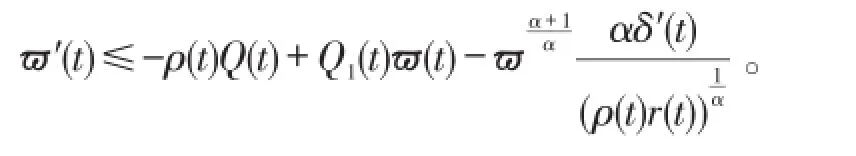
利用引理4得到

两边同乘以(t-s)n再从t0到t两边积分(t>t0)可得

由n(t-s)n-1ϖ(s)>0,可得
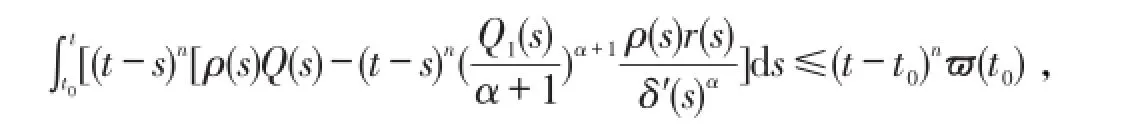
两边同除以tn可得

例1 设p(t)=0,r(t)=1,α=1,β=1,δ(t)=t,ρ(t)=1,q(t)=k1,g(t)=k2,方程(1)变为

下面利用Philos型积分平均条件,给出广义的Emden-Fowler阻尼方程(1)的振动准则。为此令

我们称函数H(t,s)∈C1(D,R)为属于F类,记作H(t,s)∈F,如果满足
(I)H(t,t)=0,t≥t0,H(t,t)>0,
(II)存在 ρ(t)∈C1([t0,∞),R+),h∈C(D0,R),使得

定理3 假设某些条件成立。设x(t)是广义的Emden-Fowler阻尼方程(1)的解,如果

则x(t)振动。
证明:假设x(t)是方程(1)的非振动解,不妨设x(t)是广义的Emden-Fowler阻尼方程(3)的最终正解(对于x(t)是广义的Emden-Fowler阻尼方程(1)的最终负解也有类似的结论),利用引理5可得

两边同乘以 H(t,s),且从t0到t(t>t0)两边积分可得

利用引理4和方程(15)可得

让t→∞,则方程(17)矛盾于方程(16)。
推论1 设x(t)是方程(1*)的解,如果

则x(t)振动。
定理4 假设某些条件成立。设x(t)是广义的Emden-Fowler阻尼方程(1)的解,如果

其中:ψ+(s)=max{ψ(s),0},则x(t)振动。
证明:假设x(t)是方程(1)的非振动解,不妨设x(t)是广义的Emden-Fowler阻尼方程(4)的最终正解(对于x(t)是广义的Emden-Fowler阻尼方程(1)的最终负解也有类似的结论),利用引理5可得

两边同乘以H(t,s),再从 T到 t(t>T)两边积分可得

同除以H(t,T)可得

利用C3可得

利用方程(18)及 C3可得
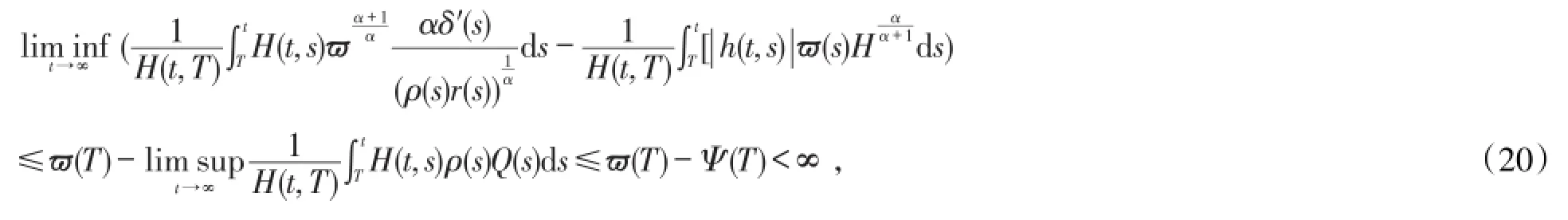
设

利用(20)可得

假设

由方程(19)可得:

方程(22)~(23)矛盾于C4。由矛盾,我们假设

设η是一个任意的正数,利用C1可得

由方程(24)可得

利用C1及方程(25)~(26)可得

利用方程(21)和(27)可得:


两边同除以G(tn)可得

利用(28)可得


利用Schwarz不等式
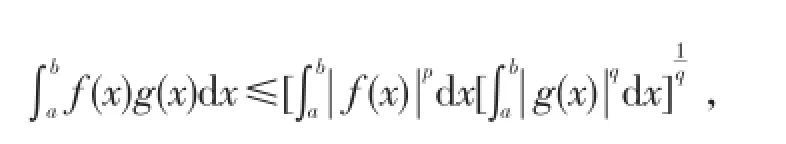
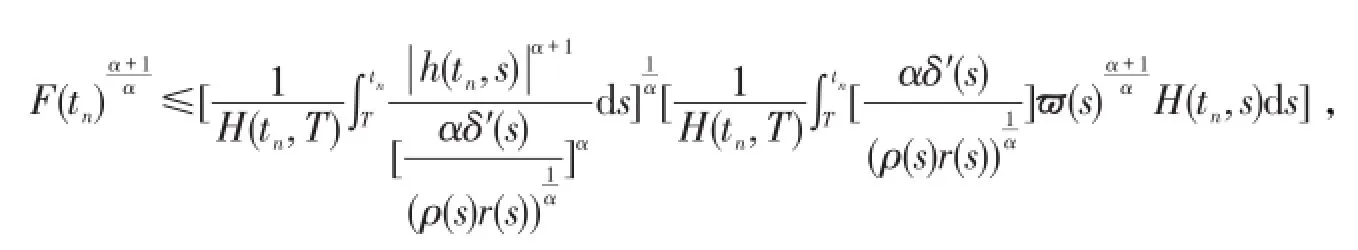
两边同除以 G(tn)可得

利用 C2可得

方程(30)~(31)与方程(29)矛盾。
推论2 设x(t)是方程(1*)的解,如果

其中:ψ+(s)=max{ψ(s),0},则x(t)振动。
[参考文献]
〔1〕PHILOS C G.On a Kamenev's integral criterion for oscillation of linear differential equa-tions of second order〔J〕.Ann Polon Math,1983,21:175-194.
〔2〕PHILOS C G.Oscillation theorems for linear differential equations of second order〔J〕.Arc-H Math,1989,53:482-492.
〔3〕YAN J.Oscillation theorems for second order linear differential equation with damping〔J〕.American Mathematical Society,1986,98:276-282.
〔4〕WONG J S W.On the generalized Emden-Fowler equation〔J〕.Slam Rev,1975,17:339-360.
〔5〕YANG X J.Oscillation criterion for a class of quasilinear differential equation〔J〕.Appl Math Comput,2004,155:451-468.
〔6〕LI H J,YEN C C.Oscillation criteria for second-order neutral delay equation〔J〕.J Comput Math Appl,1998,36:123-132.
〔7〕SUN Y G,MENG F W.Note on the paper of Dzurina and stavroulakis〔J〕.Appl Math Comput,2006,174:1634-1641.
〔8〕XU R,MENG F W.Oscillation criteria for second order quasi-linear neutral delay differenti-al equation〔J〕.Appl Math Comput,2007,192:216-222.
〔9〕LIU L H,BAI Y Z.New oscillation criteria for second order nolinear neutral delay differential equation〔J〕.J Comput Appl Math,2009,231:657-663.
〔10〕YE L H,XU Z T.Oscillation for second order quasi-linear neutral delay differential equation〔J〕.Appl Math Comput,2009,207:388-396.
〔11〕LIU H D,MENG F W,LIU P C.Oscillation and asymptotic analysis on a new generalized Emden-Fowler equation〔J〕.Appl Math Comput,2012,219:2729-2748.
Oscillation Results of a Class of Generalized Emden-Fowler Equation with Damping
Wu Bo
(College of Mathmatics and Statistic,Pu'er University,Pu'er,Yunnan 665000,China)
By using generalized Riccati transformation and integral averaging technique,this paper studies the oscillation of a class of generalized Emden-Fowler equation with damping,and establishes some new sufficient conditions for equation oscillating or converging to zero.
a generalized Emden-Fowler equation with damping;generalized Riccati transformation;oscillation criteria
O29
A
2096-2266(2016)12-0006-08
10.3969∕j.issn.2096-2266.2016.12.002
(责任编辑 袁 霞)
2016-04-24
吴波,副教授,主要从事微分方程、数理统计研究.

