耦合Burgers方程的CTE可积性及精确解
李玉娟, 胡恒春,2
(1.上海理工大学 理学院,上海 200093; 2.德克萨斯大学大河谷分校 数学系,爱丁堡 TX 78539)
耦合Burgers方程的CTE可积性及精确解
李玉娟1, 胡恒春1,2
(1.上海理工大学 理学院,上海 200093; 2.德克萨斯大学大河谷分校 数学系,爱丁堡 TX 78539)
借助符号计算软件Maple,利用CTE方法验证了耦合Burgers方程的CTE可积性,得到了耦合Burgers方程的孤子和其他波的相互作用解,包括孤子和椭圆余弦波作用解、共振多孤子解、孤子和误差函数波作用解、孤子和有理波作用解、孤子和周期波作用解.最后给出了孤子和椭圆余弦波作用解及共振多孤子解所对应的图形.
耦合Burgers方程; CTE方法; 相互作用解
孤立子理论是非线性科学的重要组成部分,孤立子理论的研究对象大多是非线性偏微分方程.随着非线性科学的飞速发展,对孤立子理论的研究也越来越多,它已成为当今科学领域的重大研究课题之一.非线性偏微分方程被用来描述流体力学、等离子物理学、非线性光学、固体物理学及环境科学等领域出现的很多非线性现象,因此,对非线性偏微分方程精确解的研究在理论和实际应用中都具有重要的意义[1].近年来,数学家和物理学家在研究过程中提出了一系列构造精确解的方法,如反散射变换法[2-4]、贝克隆变换法[5-6]、双线性变换法[7]、分离变量法[8]、达布变换法[9]、相似约化法[10-12]、Painlevé分析法[13-14]、函数展开法等.然而,除了孤子间的相互作用解,很难找到不同类型波之间的相互作用解.最近,根据非局部对称的相似约化结果,楼森岳[15]提出了consistent Riccati expansion (CRE)方法以及它的一种特殊情形consistent tanh expansion (CTE)方法.此方法不仅可以用来验证非线性发展方程的可积性,还可以更加简单地求得可积方程的各种形式的波之间的相互作用解.例如,Broer-Kaup方程[16]、Boussinesq-Burgers方程[17]、(2+1)维Boiti-Leon-Pempinelli方程[18]以及修正的Kadomstev-Petviashvili方程[19].
1 耦合Burgers方程简介
耦合Burgers方程的形式为
(1)
式中:γ为实常数;α,β是任意常数[20-21].
该模型是Esipov[22]研究多分散性沉积模型时推导出的在重力作用下悬浮液或胶质物中两种粒子按比例缩小的体积浓度的演变模型,在凝聚态物理和流体动力学等领域都有着广泛的应用.近年来,许多学者利用多种方法得到了耦合Burgers方程的多种形式的精确解,例如,用tanh函数展开法得到耦合Burgers方程的孤子解[23],用Hirota双线性法得到耦合Burgers方程的多孤子解[24]等.本文将利用CTE方法来求解耦合Burgers方程.
作适当的标度变换,可以将方程(1)变为
(2)
即相当于在方程(1)中取γ=1,α=β=-1.本文对方程(2)进行研究.
2 耦合Burgers方程CTE可积性
对于给定的非线性偏微分方程
(3)
要寻找具有如下形式的截断展开解:
(4)
式中,n由方程(3)的领头项分析(平衡最高阶导数项和最高阶非线性项)决定.
将式(4)代入方程(3),令tanhi(ω)的系数为0,得到包含ui和ω以及它们的各阶导数的系统.
定义 对于非线性偏微分方程(3),将解式(4)代入其中,令tanhi(ω)的系数为0,得到包含ui(i=0,1,2,…,n)和ω以及它们的各阶导数的系统,如果这个系统是相容的或非超定的,则称方程(3)是consistent tanh expansion (CTE)可积的.
对耦合Burgers方程(2)进行领头项分析,得到如下截断tanh展开式:
(5)
将式(5)代入耦合Burgers方程(2),得
令tanhi(ω)的系数为零,可以得到含有5个未知量u0,u1,v0,v1,ω的8个超定方程:
可得
及ω满足的相容性条件方程
(6)
其中
且S和C是Möbius变换
下的不变量.根据定义,可以判定耦合Burgers方程(2)是CTE可积的.综上所述,可以概括出定理1.
定理1 如果ω是相容性条件方程(6)的一个解,那么,
(7)
是耦合Burgers方程(2)的CTE解.
3 耦合Burgers方程的精确解
根据定理1,通过求解相容性条件方程(6),可以找到不同形式的相互作用解.为了求解方程(6),将方程(6)写成下面的形式:
(8a)
(8b)
从上面的方程中可知,通过Burgers方程(8b)的一个固定解就可以求解变系数势Burgers方程(8a),从而得到函数ω的解.因此,耦合Burgers方程(2)的相应解可以从CTE解式(7)中得到.
3.1 简单孤子解
方程(8)有如下的平凡解:
(9)
式中,k0,w0,d0是任意常数.
将式(9)代入式(7),可以得到耦合Burgers方程(2)的简单孤子解
(10)
3.2 孤子与椭圆余弦波作用解
为了得到耦合Burgers方程(2)的孤子和椭圆余弦波的相互作用解,考虑如下形式的ω函数:
(11)

其中
a4=4
并且k1w0=k0w1,a2,a3为任意常数.
很显然,方程(12)的通解是由椭圆函数定义的,即可以用一些椭圆函数(例如,Jacobi椭圆函数sn(ζ),cn(ζ),dn(ζ))来构造ω的表达式,从而得到耦合Burgers方程(2)的新解.假定关于ω的函数具有如下形式:
式中,Ef是第一类不完全可积椭圆函数.
将式(13)带入方程(6)中,令Jacobi椭圆函数不同次幂的系数为零,通过计算,可得m=n且A,n,k0,k1,w0,w1为任意非零常数.
将m=n及式(13)代入式(7)中,得到耦合Burgers方程(2)的孤子和椭圆余弦波作用解,省略u和v复杂的函数表达式,对任意常数进行如下的取值:
k1=2,w0=4,w1=3
(14)
可以得到u和v的结构图,如图1所示(见下页).
3.3 孤子与势Burgers波作用解
为了找出耦合Burgers方程(2)的孤子和其他波的相互作用解,考虑如下形式的ω函数:
(15)
式中,g是关于x,t的函数.

图1 孤子和椭圆余弦波作用解u和v的结构图
将式(15)代入方程(8a),得到
为了进一步的简化,将f取为最简单的常数解.
(17)
这样,方程(16)就化为一个常数系数势Burgers方程
(18)
将式(15)和式(18)代入式(7),得到耦合Burgers方程(2)的孤子和势Burgers波的相互作用解
(19)
势Burgers方程有多类已知的精确解,例如,共振孤子解、误差函数解.现用方程(18)的已知解来构造孤子和势Burgers波的相互作用解.
3.3.1 共振多孤子解
不难验证,方程(18)有如下形式的解:
(20)
式中:ki是任意常数;wi满足色散关系
将式(20)代入式(19),可以得到耦合Burgers方程(2)的(n+1)共振孤子解.如果在取n=1的情况下,再取
(21)
可以得到扭结型孤波解u和v的结构图,如图2所示.
在取n=2的情况下,再取
(22)
扭结型孤波解u和v的结构图如图3所示.
3.3.2 孤子与误差函数波作用解
势Burgers方程(18)有误差函数解
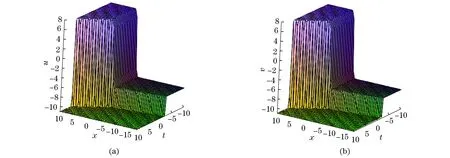
图2 扭结型孤波解u和v的结构图(n=1)
(23)

显然,式(23)和解式(19)呈现了耦合Burgers方程(2)的孤子与误差函数相互作用解.
3.3.3 孤子与自由形状波相互作用解
势Burgers方程(18)可以线性化为热传导方程[25]
从而,可以得到一个势Burgers方程(18)的通解
其中,任意函数F(z)为
解式(19)和式(24)是孤子与任意F波的相互作用解.
3.3.4 孤子与有理波相互作用解
如果将F看作z的多项式解,即
(26)
式中,cn是任意常数,则
(27)
式中,Γ(x)是伽马函数.
解式(19)和式(27)变成了孤子和有理波的相互作用解.
3.3.5 孤子与周期波相互作用解
将任意函数F取成如下的特殊形式:
(28)
式中,aj,bj,cj,dj是任意常数,则
显然,解式(19)和式(29)是孤子和周期波的相互作用解.
4 结 论
利用CTE方法对耦合Burgers方程进行了研究,验证了耦合Burgers方程的CTE可积性.然后通过选取相容性条件方程的ω的不同解,得到了耦合Burgers方程的孤子和其他波的相互作用解,包括孤子和椭圆余弦波作用解、共振多孤子解、孤子和误差函数波作用解、孤子和有理波作用解、孤子和周期波作用解.通过选取适当的常数,得到了一些解的结构图.
[1] 谷超豪.孤立子理论与应用[M].杭州:浙江科学技术出版社,1990.
[2] GARDNER C S,GREENE J M,KRUSKAL M D,et al.Method for solving the Korteweg-de Vries equation[J].Physical Review Letters,1967,19(7):1095-1097.
[3] FOKAS A S,ABLOWITZ M J.On the inverse scattering transform of multidimensional nonlinear equations related to first-order systems in the plane[J].Journal of Mathematical Physics,1984,25(8):2094-2505.
[4] ABLOWITZ M J,CLARKSON P A.Solitons,nonlinear evolution equations and inverse scattering[M].Cambridge:Cambridge University Press,1991:721-725.
[5] WAHLQUIST H D,ESTABROOK F B.Bäcklund transformation for solutions of the Korteweg-de Vries equation[J].Physical Review Letters,1973,31(23):1386-1390.
[6] KONNO K,WADATI M.Simple derivation of Bäcklund transformation from Riccati form of inverse method[J].Progress of Theoretical Physics,1975,53(6):1652-1656.
[7] HIROTA R.Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons[J].Physical Review Letters,1971,27(18):1192-1194.[8] YANG L J,DU X Y,YANG Q F.New variable separation solutions to the (2+1)-dimensional Burgers equation[J].Applied Mathematics and Computation,2016,273(15):1271-1275.
[9] MATVEEV V B,SALLE M A.Darboux transformations and solitons[M].Berlin:Springer-Verlag,1991.
[10] CLARKSON P A,KRUSKAL M D.New similarity reductions of the Boussinesq equation[J].Journal of Mathematical Physics,1989,30(10):2201-2213.
[11] LOU S Y,MA H C.Non-Lie symmetry groups of (2+1)-dimensional nonlinear systems obtained from a simple direct method[J].Journal of Physics A:Mathematical and General,2005,38(7):129-137.
[12] 胡潇,胡恒春.非线性耦合Harry-Dym方程的对称约化[J].上海理工大学学报,2016,38(1):8-12.
[13] WEISS J,TABOR M,CARNEVALE G.The Painlevé property for partial differential equations[J].Journal of Mathematics Physics,1983,24(3):522-526.
[14] WEISS J.On classes of integrable systems and the Painlevé property[J].Journal of Mathematics Physics,1984,25(1):13-24.
[15] LOU S Y.Consistent Riccati expansion for integrable systems[J].Studies in Applied Mathematics,2015,134(3):372-402.
[16] CHEN C L,LOU S Y.CTE solvability and exact solution to the Broer-Kaup system[J].Chinese Physics Letters,2013,30(11):110202,1-5.[17] WANG Y H.CTE method to the interaction solutions of Boussinesq-Burgers equations[J].Applied Mathematics Letters,2014,38:100-105.
[18] WANG Y H,WANG H.Symmetry analysis and CTE solvability for the (2+1)-dimensional Boiti-Leon-Pempinelli equation[J].Physica Scripta,2014,89(12):125203,1-5.
[19] REN B.Interaction solutions for mKP equation with nonlocal symmetry reductions and CTE method[J].Physica Scripta,2015,90(6):065206,1-8.
[20] ZHANG R P,YU X J,ZHAO G Z.Local discontinuous Galerkin method for solving Burgers and coupled Burgers equations[J].Chinese Physics B,2011,20(11):110205,1-6.
[21] MITTAL R C,ARORA G.Numerical solution of the coupled viscous Burgers' equation[J].Communications in Nonlinear Science and Numerical Simulation,2011,16(3):1304-1313.
[22] ESIPOV S E.Coupled Burgers equations:a model of polydispersive sedimentation[J].Physical Review E,1995,52(4):3711-3718.
[23] JAWAD A J M,PETKOVIC M D,BISWAS A.Soliton solutions of Burgers equations and perturbed Burgers equation[J].Applied Mathematics and Computation,2010,216(11):3370-3377.
[24] ABDOU M A,SOLIMAN A A.On completely integrable coupled Burgers and coupled Korteweg-de Vries systems[J].Applied Mathematics Letters,2012,25(12):2052-2057.
[25] 王跃明,张金良,王明亮.变系数Burgers方程的BT与非线性边值-初值问题[J].洛阳工学院学报,2000,21(3):83-86.
(编辑:石 瑛)
CTE Solvability and Exact Solutions of a Coupled Burgers Equation
LI Yujuan1, HU Hengchun1,2
(1.CollegeofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China; 2.DepartmentofMathematics,TheUniversityofTexasRioGrandeValley,Edinburg,TX78539,USA)
With the help of symbolic computation software Maple,by using the CTE method,a coupled Burgers equation was proved to be CTE solvable.Many interaction solutions among solitons and other types of nonlinear excitations of the coupled Burgers equation were obtained,which include soliton-cnoidal waves,multiple resonant solutions,soliton-error function waves,soliton-rational waves,and soliton-periodic waves.The corresponding graphs of the soliton-cnoidal waves and multiple resonant solutions were presented.
coupledBurgersequation;CTEmethod;interactionsolutions
1007-6735(2016)06-0517-06
10.13255/j.cnki.jusst.2016.06.002
2016-05-26
上海市自然科学基金资助项目(10ZR1420800);上海市重点学科建设资助项目(XTKX2012);国家自然科学基金资助项目(11071164,11201302)
李玉娟(1992-),女,硕士研究生.研究方向:孤立子理论与可积系统.E-mail:liyujuanmath@163.com
胡恒春(1976-),女,副教授.研究方向:孤立子理论与可积系统.E-mail:hhengchun@163.com
O 175
A

