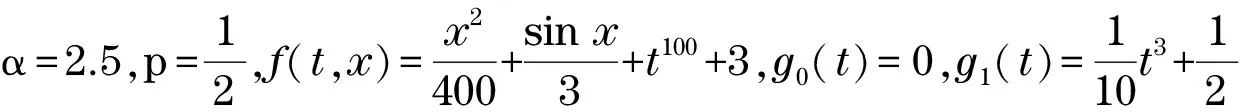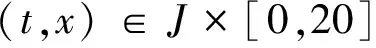具逐项分数阶导数的积分边值问题正解的存在性
李 燕, 刘锡平, 李晓晨, 张 莎
(上海理工大学 理学院,上海 200093)
具逐项分数阶导数的积分边值问题正解的存在性
李 燕, 刘锡平, 李晓晨, 张 莎
(上海理工大学 理学院,上海 200093)
研究了一类具有逐项分数阶导数的微分方程积分边值问题正解的存在性和多解性.利用锥上不动点定理和 Leggett-Williams不动点定理,分别得到了该积分边值问题至少存在1个正解和3个正解的结论.最后给出2个例子来证明结论有效.
分数阶微分方程; 逐项分数阶导数; 积分边值问题; 锥上不动点定理; 正解
1 问题的提出
分数阶微分方程在流变学、力学、信号处理和系统辨识、神经网络、分形和混沌等领域有着广泛的应用.近年来,国内外学者对其理论的研究取得了许多有价值的成果[1-2],为了描述运动过程的整体性态,对于分数阶微分方程积分边值问题的研究显得尤为重要,可参见文献[3-7].在振动理论中,低阶导数项(如阻尼项)具有重要的作用,为了了解它们对系统的影响,不少学者对具有逐项分数阶导数的微分方程进行了研究[8-13].
本文主要研究一类具有逐项分数阶导数的微分方程积分边值问题
(1)

2 预备知识及引理
有关分数阶积分及Caputo分数阶导数的定义参见文献[1-2].
引理1 设0 等价.其中, 两端,运用分数阶微积分的相关理论,可得 c0+c1t+c2t2+…+cntn 并且 由边界条件可得 所以 反之,若x=x(t)是积分方程(2)的解,由分数阶微分方程的相关理论容易验证其满足边值问题(1). 引理2G(t,s)具有下列性质: a.G(t,s)连续且G(t,s)≥0,对任意的(t,s)∈J×J; H0假设g0,g1∈C(J),使得函数H(t,s)满足: 定义线性算子A:C(J)→C(J): (3) 引理3 设I为恒等算子,若假设H0成立,则算子A具有如下性质: a.A是有界线性算子; b.A(P)⊂P; c.I-A可逆; 证明a-c结论是显然的,这里只给出d的证明过程. 令x(t)=y(t)+Ax(t),得到x(t)=(I-A)-1y(t),t∈J,y∈C(J).由算子A的定义可知积分方程 因此 (4) 并且,由0≤m≤H(t,s) 从而 于是 结论成立. 如果d=c,那么,由引理5的条件a可以推出条件c. (5) 再由式(4)以及引理3可知,x(t)是问题(1)的解当且仅当x(t)是x(t)=(I-A)-1Tx(t)=Sx(t)的解,即x(t)是S的不动点,其中, 定理1 设H0成立,并且f(t,x)是J×+→+上的连续函数,若存在2个正常数r2>r1>0使得: H2f(t,x)≤α(1-p)(1-M)r2,(t,x)∈J×[0,r2]. 证明 由引理2和假设H0,易证S: P→P. 现证S:P→P 全连续. 另一方面,对任意的t1,t2∈J, 即S(P0)等度连续.综上所述,S是全连续算子. 所以 所以 定理2 设H0成立,并且f(t,x)是J ×+→+上的连续函数,若存在常数0 H3f(t,x)≤α(1-p)(1-M)a,(t,x)∈J×[0,a] ; H5f(t,x)≤α(1-p)(1-M)c,(t,x)∈J×[0,c]. 则边值问题(1)至少有3个正解x1,x2,x3,且满足: 即φ(Sx)>b,对所有的x∈P(φ,b,c).这表明引理5的条件a满足. 由引理5可知,边值问题(1)至少有3个正解x1,x2,x3,且满足: 为了证明结论的有效性,现给出2个例子. 例1 考虑边值问题 (7) 由定理1可得此边值问题(7)至少有1个正解. 例2 考虑边值问题 (8) 这里取 那么,由定理2可知,此边值问题(8)至少有3个正解x1,x2,x3,且满足: [1] KILBAS A A,SRIVASTAVA H M,Trujillo J J.Theory and applications of fractional differential equations[M].Amsterdam: Elsevier Beasloten Vennootschap,2006. [2] 白占兵.分数阶微分方程边值问题理论及应用[M].北京: 中国科学技术出版社,2012. [3] JIA M,LIU X P.Multiplicity of solutions for integral boundary value problems of fractional differential equations with upper and lower solutions[J].Applied Mathematics and Computation,2014,232:313-323. [4] LIN L G,LIU X P,FANG H Q.Method of upper and lower solutions for fractional differential equations[J].Electronic Journal of Differential Equations,2012(100):596-602. [5] 靳威,寇春海.分数阶微分方程积分边值问题正解的存在性[J].东华大学学报(自然科学版),2013,39(5):695-698. [6] JIA M,LIU X P.Three nonnegative solutions for fractional differential equations with integral boundary conditions[J].Computers and Mathematics with Applications,2011,62(3):1405-1412. [7] 刘帅,贾梅,秦小娜.带积分边值条件的分数阶微分方程解的存在性和唯一性[J].上海理工大学学报,2014,36(5):409-415. [8] 李燕,刘锡平,李晓晨,等.具有逐项分数阶导数的微分方程边值问题解的存在性[J].纯粹数学与应用数学,2016,32(5):470-480. [9] 李秀红,寇春海,刘晓波.分数阶微分方程边值问题解的存在性[J].东华大学学报(自然科学版),2011,37(2):240-245. [10] ALSAEDI A,NTOUYAS S K,AGRWAL R P,et al.On caputo type sequential fractional differential equations with nonlocal integral boundary conditions[J].Advances in Difference Equations,2015,2015(1):1-12. [11] AHMAD B,NIETO J J.Sequential fractional differential equations with three-point boundary conditions[J].Computer and Mathematics with Applications,2012,64(10):3046-3052. [12] CHAI G Q.Existence results for boundary value problems of nonlinear fractional differential equations[J].Computers and Mathematics with Applications,2011,62(5):2374-2382. [13] 吴贵云,刘锡平,杨浩.具有微分算子的分数阶微分方程边值问题解的存在性与唯一性[J].上海理工大学学报,2015,37(3):205-209. (编辑:石 瑛) Existence of Positive Solutions for the Integral Boundary Value Problem of Sequential Fractional Differential Equations LI Yan, LIU Xiping, LI Xiaochen, ZHANG Sha (CollegeofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China) The existence and multiplicity of positive solutions were investigated for a class of integral boundary value problems of fractional differential equations with sequential fractional derivatives.The existence of at least one positive solution and three positive solutions for integral boundary value peroblems was obtained respectively,by using the fixed point theorem on cone and the Leggett-Williams fixed point theorem.Two examples were given to illustrate the results. fractionaldifferentialequation;sequentialfractionalderivative;integralboundaryvalueproblem;fixedpointtheoremoncone;positivesolution 1007-6735(2016)06-0511-06 10.13255/j.cnki.jusst.2016.06.001 2016-07-01 国家自然科学基金资助项目(11171220);沪江基金资助项目(B14005) 李 燕(1991-),女,硕士研究生.研究方向:常微分方程理论与应用.E-mail:764250156@qq.com 刘锡平(1962-),男,教授.研究方向:常微分方程理论与应用.E-mail:xipingliu@163.com O 175.8 A
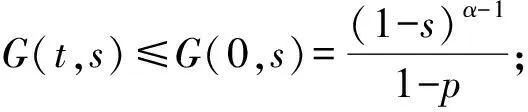
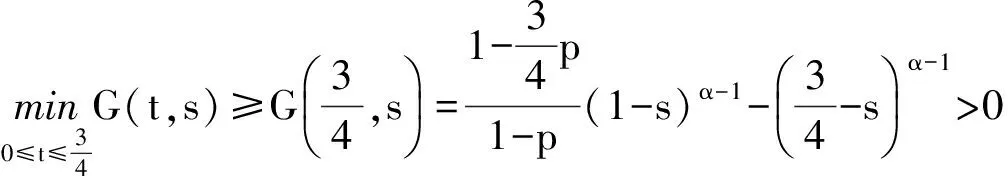



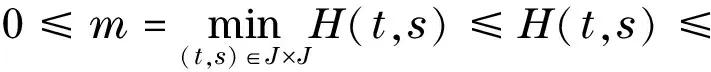


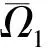
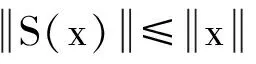
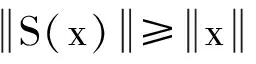
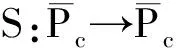

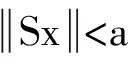


3 积分边值问题正解的存在性和多解性


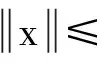
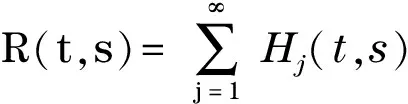
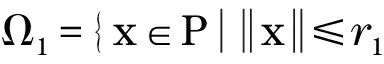
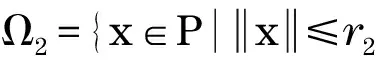
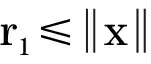

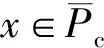

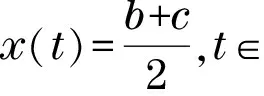
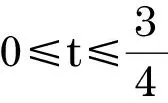
4 应用举例