负泊松比负热膨胀超材料微结构拓扑优化设计

王 昱, 吕恩利, 王亚娟, 王飞仁, 林小娟

(华南农业大学 工程学院,广州 510642)

负泊松比负热膨胀超材料微结构拓扑优化设计

王 昱, 吕恩利, 王亚娟, 王飞仁, 林小娟

(华南农业大学 工程学院,广州 510642)

提出一种拓扑优化设计方法,用于设计同时具有负泊松比和负热膨胀系数的超材料.超材料是人工设计的复合材料,由微米或纳米结构的周期性阵列组成,并具有天然材料难以具备的超常物理性质.基于拓扑优化理论,建立了一个表示多材料微观结构的多相边界的水平集模型,并采用数值均匀化方法来计算微观结构的等效性能,然后通过参数化水平集优化方法实现边界形状的演变和拓扑结构的设计.通过两个数值算例,给出超材料微结构材料分布的优化结果,证明了设计方法的可行性,为实现具备特殊性能的人工材料设计提供了一套系统的设计方法.

超材料; 拓扑优化; 水平集方法; 负泊松比; 负热膨胀

在工程应用中,温度变化会引起尺寸变化,所以必须考虑材料和结构的膨胀与收缩.由于大多数材料的应用环境将经历一系列的工作温度,无论是技术还是基础研究领域都会关注由温度变化引起的结构的热膨胀[10].热膨胀系数是一个重要的物理量,用来测量温度对材料尺寸的改变程度.负热膨胀材料(NTE)在一定的温度升高范围内呈现收缩的热弹性能.相关研究证明,由三相材料组成的复合材料的性能可以超越其中单相材料的性能[11].因此,极端的热弹性能的材料通常是通过组合三相传统的材料,如金属或塑料等,得到一个新的具有周期结构的复合材料.

泊松比[1]被定义为在单轴拉伸条件下,横向收缩应变与纵向拉伸应变的比值,这是衡量弹性材料性能的基本指标.弹性理论允许泊松比为负,但大多数传统材料泊松比为正.与正泊松比的常规材料相比,具有负泊松比的材料(NPR)表现出非常规的属性,即横向拉伸时纵向膨胀,横向收缩时纵向压缩.由于广泛的应用潜力,自从早期研究工作以来[12],负泊松比材料已经吸引了越来越多的关注.到目前为止,已有一些方法开发设计拉胀材料[13-15],但鲜有系统的设计方法用于设计同时表现NPR和NTE的超材料.

拓扑优化已被确定为是在结构优化领域最有前途的技术之一[16],其中,水平集方法因其具有光滑的设计边界,并集成了形状优化和拓扑优化,已经成为一种备受关注的形状结构拓扑优化方法.特别是参数化水平集方法(PLSM)[17],已被证明是一个最强大的主流拓扑形状优化的结构和机制.它能很好地继承传统水平集方法的优点,并使许多有效的基于梯度的优化算法[18]直接应用到水平集方法中[19].

因此,本文基于多相水平集模型来设计同时具有NPR和NTE的超材料拓扑形状.多相水平集模型是一个显示多材料的边界的水平集函数,该函数能避免设计域出现材料重叠与空白.文中还将采用基于PLSM的超材料微结构设计方法.在这种方法中,应用了数值均匀化方法来计算复合材料的宏观等效性能,并使用PLSM来实现形状和多材料微结构拓扑演变.最后,通过两个典型的数值算例证明所提出方法的有效性.

1 拓扑优化方法

1.1 参数化水平集方法

在水平集方法(LSM)方法中,设计边界通过高维水平集函数的零水平集形成的隐式边界表达[20-21].一个水平集函数Φ(x)要求在参考域D内具有Lipschitz连续性.对于本文涉及的多相材料设计问题,采用m个水平集函数相结合来描述m+1相材料,包括无材料相(即孔洞)和m相固体材料.固体材料、边界及孔洞的水平集表达式分别为

(1)

式中:I=1,…,m为某一水平集函数;m是水平集函数的总数;D为设计参考域,包括所有允许的微观结构的形状;ΩI是函数值为正的水平集函数;∂ΩI表示第I个水平集函数的设计边界.

我最喜欢的蔬菜是西红柿。西红柿圆圆的，像个小灯笼似的。它的颜色各异：有的是粉色的，上面还隐隐约约的白点，妈妈说这样的西红柿是沙瓤的，吃起来更美味；有的是红红的，像是小姑娘羞红了的脸蛋，越看越可爱，我都有点不舍得吃了；还有黄绿相间的西红柿，据说是科学家叔叔们发明的新品种，闻起来有股淡淡的清香，吃起来酸甜可口，味道纯正，科学家叔叔们真了不起！

在PLSM方法中,采用紧支径向基函数(CS-RBF)插值得到高维水平集函数,有利于平衡插值精度和效率.原来的水平集函数可以用CS-RBF在预先指定节点的插值表达,即

形状函数向量为

(3)

扩展系数向量为

(4)

式中:N是设计域内CS-RBF节点总数;t为虚拟时间.

通过CS-RBFs插值可实现时间和空间的分离:形状函数为空间函数,膨胀系数仅与时间相关.值得注意的是,用于插值每个隐式水平集函数的CS-RBFs是相同的.因此,解耦汉密尔顿-雅各比偏微分方程(H-J PDE)的时间相和空间相可得

(5)

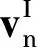
(6)

由式(6)可知,正速度矢量所涉及的项都是通过设计域内的节点求得,因此正速度扩展到了整个设计领域.这样,基于偏微分方程的水平集方程已转化为代数方程.优化唯一的未知数是插值的膨胀系数,在优化设计中定义为设计变量,并使用更高效的优化算法进行迭代.

1.2 三相复合材料的材料模型

通过材料模型[5],在设计域内的任何计算点x的弹性常数C和热应变系数α可以由两个水平集函数Φ1和Φ2计算得出.

(7)

(8)

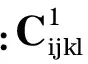
1.3 超材料微结构的形状拓扑优化

将在给定的设计域,单胞Y,进行形状拓扑优化.复合材料的等效弹性张量和热弹系数采用均匀化方法计算,得

(9)

(10)

(11)

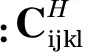
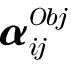
(12)

(13)

由于水平集函数的参数化,许多更高效的基于梯度的优化算法可用于求解优化问题,例如:移动渐近线法(MMA)[18].采用MMA需要提供目标函数和约束条件的关于设计变量的一阶导数.目标函数关于设计变量的一阶导数表示为

其中,

式中:χij为位移场;αpq为局部热应变场.

体积约束相对于设计变量的导数为

(18)

式中,δ为狄拉克函数,是Heaviside函数的一阶导数.

2 数值算例

用来计算位移场,设计域采用4个节点的四边形单元离散,且水平集的节点与四边形单元的节点一致.优化过程中,水平集函数采用MMA方法更新设计变量.收敛准则为连续两次迭代的目标函数值差小于10-4,或最大迭代次数达到200次(基于数值试验).设定两相虚拟固体材料的弹性模量:E1=E2=1;泊松比:v1=v2=0.3;热膨胀系数:α1=1,α2=10.

2.1 算例1

算例1设计了一种正交各向异性材料,以实现负的泊松比(-0.5),以及其在垂直方向上的负热应变系数(-0.3).两相固体材料体积分数分别为0.3和0.1.拓扑形状的演化和收敛过程如图1所示.红色区域表示固体材料相1,蓝色区域表示固体材料相2,而白色区域是孔洞.两个水平集的表面和对应于所得到的拓扑结构的两个固相的零水平集轮廓.式(19)为优化所得弹性张量与热膨胀系数.

(19)

由式(19)可知,优化后材料的泊松比为-0.446 3,垂直方向热应变系数为-0.261 6.

从算例1的迭代过程可以注意到,形状拓扑优化设计方法的特点是拥有光滑的材料边界和明显的界线[20-21].此外,在优化过程中,所提出的方法不仅可以合并初始设计中的孔洞,也可以创建新的孔洞,以实现最佳的拓扑结构的基本单元.基于所得到的最优设计(如图2所示),注意到所得的微结构的拓扑结构与文献[9]所获得的结果相似.可知等效的弹性和热弹性能是依赖于施加的负载后单胞的内部结构和变形的方式.因此,设计一种具有极限性能的复合材料,微结构的设计将会出现类似旋转刚性机构[1-2]的结构.

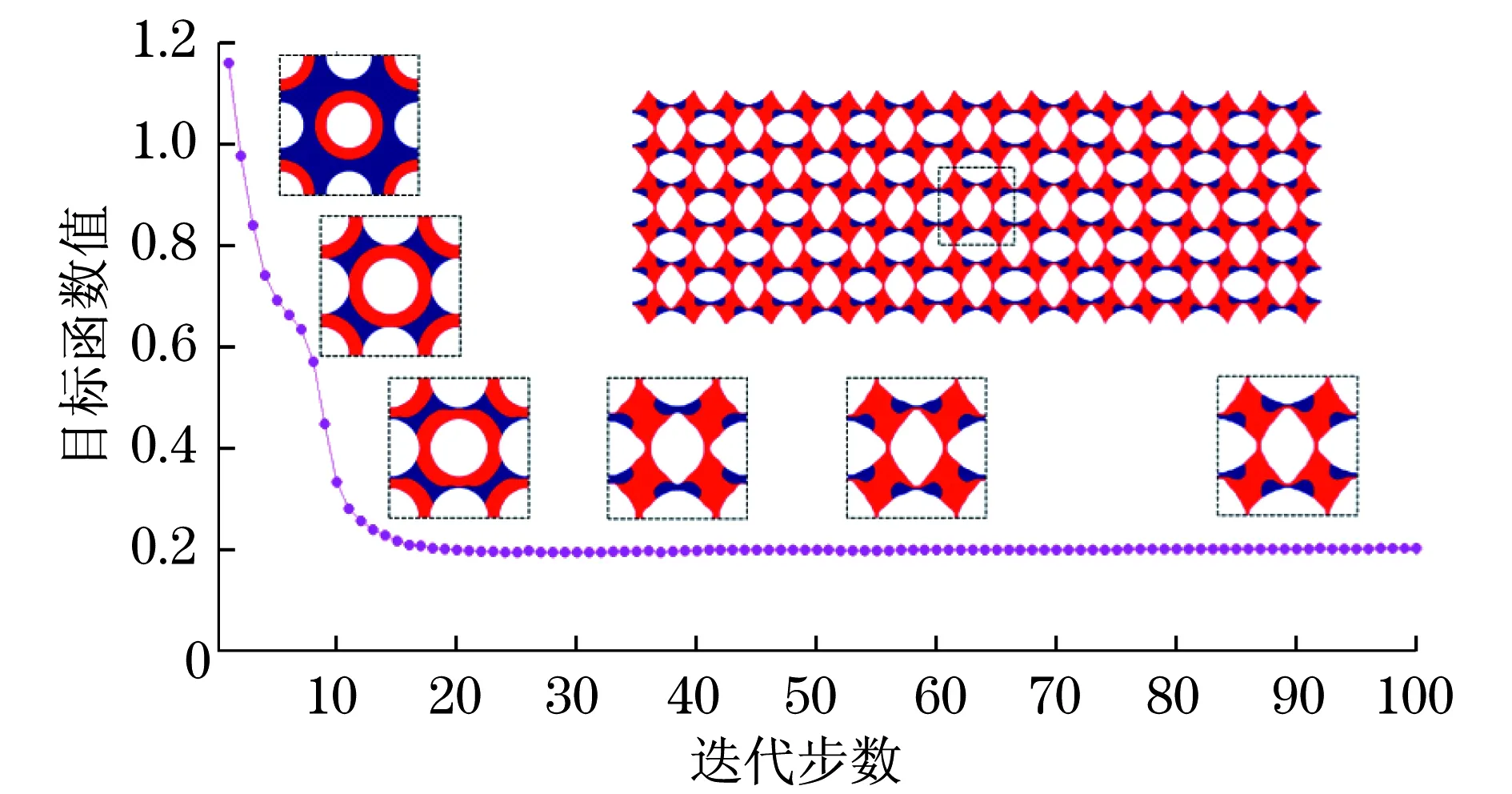
图1 目标函数的收敛过程(算例1)

图2 固体材料相轮廓图(算例1)

2.2 算例2

算例2设计了一个正交各向异性材料,以实现负的泊松比(-0.65),以及在水平方向上的负热应变系数,且热应变系数达到极小值.两相固体材料体积分数分别为0.25和0.10.拓扑形状的演化和收敛过程如图3所示,式(20)为优化所得弹性张量.

(20)

由式(20)可知,优化后材料的泊松比为-0.644 2,水平方向热应变系数为-3.356.

式(20)结果表明,极端的热膨胀的形成会导致一个非常低的结构刚度,即实现一个方向的极端热应变将导致在另一个方向上的一个极端的刚度.因此,在一个特定的方向设计极端热膨胀材料,应在优化约束中定义另一方向上的最小刚度值,使设计具有物理意义.在算例2中,设定垂直方向的体积模量的下限为0.09.

材料的等效弹性和热弹性能取决于基本单元的内部结构和变形方式,为使微结构在加载时发生旋转,凹角结构的生成是使结构发生较大旋转效果的关键.在微结构的特定布局下,可以通过类似旋转刚性机构的微结构基本单元之间的角度变化,使多孔复合材料整体变形,达到负的极端力学性能指数,即

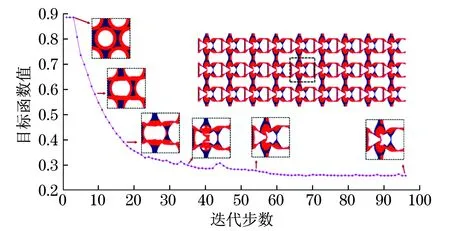
图3 目标函数的收敛过程(算例2)

负泊松比和负热膨胀系数.在上述两个数值例子中,可发现最佳的泊松比和热应变系数不能准确地接近规定的值.由于拓扑形状优化最初是连续体结构的一种设计方法,它实际上是利用结构的变形来近似模拟刚体的旋转效应,因此难以使微结构实现如刚性连杆机构般的旋转变形.在优化过程中会发生在折返结构部分的类似铰链结构断开的现象,为保证优化所得的结果为连续体结构,所得结果无法准确地达到设定的泊松比和热应变系数.尽管如此,该方法仍然提供了一个系统的复合材料微结构设计方法,使材料同时达到预期的负泊松比和负热膨胀系数.

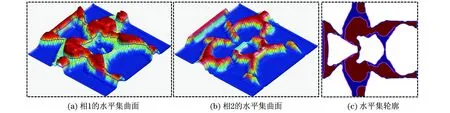
图4 固体材料相轮廓图(算例2)

3 结 论

利用数值均匀化方法和参数化的水平集方法,提出了同时具有NPR和NTE性质复合材料的系统设计方法.数值算例的结果验证了所提出的拓扑形状设计方法的有效性.材料微结构设计可以从二维推广到三维,但计算成本将显著增加.同时,该方法具有拓展至其他类型超材料设计的潜力.

[1] EVANS K E,ALDERSON A.Auxetic materials:functional materials and structures from lateral thinking![J].Advanced Materials,2000,12(9):617-628.

[2] LAKES R.Cellular solid structures with unbounded thermal expansion[J].Journal of Materials Science Letters,1996,15(6):475-477.

[3] GAO Y,ZHOU N,YANG F,et al.P-phase precipitation and its effect on martensitic transformation in (Ni,Pt)Ti shape memory alloys[J].Acta Materialia,2012,60(4):1514-1527.[4] GAO Y,ZHOU N,WANG D,et al.Pattern formation during cubic to orthorhombic martensitic transformations in shape memory alloys[J].Acta Materialia,2014,68:93-105.

[5] SIGMUND O.A new class of extremal composites[J].Journal of the Mechanics and Physics of Solids,2000,48(2):397-428.

[6] GUEST J K,PRÉVOST J H.Design of maximum permeability material structures[J].Computer Methods in Applied Mechanics and Engineering,2007,196(4/5/6):1006-1017.

[7] 张卫红,汪雷,孙士平.基于导热性能的复合材料微结构拓扑优化设计[J].航空学报,2006,27(6):1229-1233.

[8] 孙士平,张卫红.多相材料微结构多目标拓扑优化设计[J].力学学报,2006,38(5):633-638.

[9] 孙良奎,于哲峰,黄洁.基于超材料的平板二维定向传热结构设计[J].物理学报,2015,64(22):0224401.

[10] SIGMUND O,TORQUATO S.Composites with extremal thermal expansion coefficients[J].Applied Physics Letters,1996,69(21):3203-3205.

[11] LAKES R.Materials with structural hierarchy[J].Nature,1993,361(6412):511-515.

[12] LAKES R.Foam structures with a negative Poisson's ratio[J].Science,1987,235(4792):1038-1040.

[13] YANG W,LI Z M,SHI W,et al.Review on auxetic materials[J].Journal of Materials Science,2004,39(10):3269-3279.

[14] 曹先凡,刘书田.基于拓扑描述函数的特定性能材料设计方法[J].固体力学学报,2006,27(3):217-222.

[15] 宋迎东,孙杰,孙志刚,等.基于遗传算法的复合材料细观结构拓扑优化设计[J].固体力学学报,2009,30(4):416-423.

[16] BENDSOE M P,SIGMUND O.Topology optimization:theory,methods and applications[M].Berlin Heidelberg:Springer-Verlag,2004.

[17] LUO Z,TONG L Y,WANG M Y,et al.Shape and topology optimization of compliant mechanisms using a parameterization level set method[J].Journal of Computational Physics,2007,227(1):680-705.

[18] SVANBERG K.The method of moving asymptotes—a new method for structural optimization[J].International Journal for Numerical Methods in Engineering,1987,24(2):359-373.

[19] BELYTSCHKO T,XIAO S P,PARIMI C.Topology optimization with implicit functions and regularization[J].International Journal for Numerical Methods in Engineering,2003,57(8):1177-1196.

[20] ALLAIRE G,JOUVE F,TOADER A M.Structural optimization using sensitivity analysis and a level-set method[J].Journal of Computational Physics,2004,194(1):363-393.

[21] WANG M Y,WANG X M,GUO D M.A level set method for structural topology optimization[J].Computer Methods in Applied Mechanics and Engineering,2003,192(1/2):227-246.

(编辑:丁红艺)

Topology Optimization Design of Microstructured Metamaterials with Negative Poisson’s Ratio and Negative Thermal Expansion

WANG Yu, LÜ Enli, WANG Yajuan, WANG Feiren, LIN Xiaojuan

(CollegeofEngineering,SouthChinaAgriculturalUniversity,Guangzhou510642,China)

A level set-based method was introduced to design the metamaterials which can exhibit negative Poisson’s ratio and negative thermal expansion simultaneously.Negative Poisson’s ratio (also called auxeticity) and negative thermal expansion are phenomena that may rarely be found in the nature materials.It is now known that these unusual properties are mainly dependent on the particular features in the material’s micro- or nano- structural deformation when subjected to a thermal or mechanical load.A numerical homogenization method was applied to evaluate the effective properties of the microstructure,and the multi-phase level set method was used to implement the shape and topology evolutions of the microstructure.Two numerical examples were given to demonstrate the feasibility of the proposed topology optimization method,which provides a systematic design method for the design of artificial materials with special properties.

metamaterial;topologicalshapeoptimization;letsetmethod;negativePoisson’sratio;negativethermalexpansion

1007-6735(2016)06-0551-06

10.13255/j.cnki.jusst.2016.06.008

2016-09-08

广东省农产品冷链物流装备工程技术研究中心建设项目(2016B090920092);华南农业大学高水平青年科技人才培育基金项目(216262)

王 昱(1987-),女,讲师.研究方向:结构拓扑优化、汽车轻量化设计等.E-mail:yu-wang@scau.edu.cn

吕恩利(1979-),男,教授.研究方向:果蔬冷链物流技术与装备、交通运输、汽车维修检测等.E-mail:enlilv@scau.edu.cn

TH 122

A