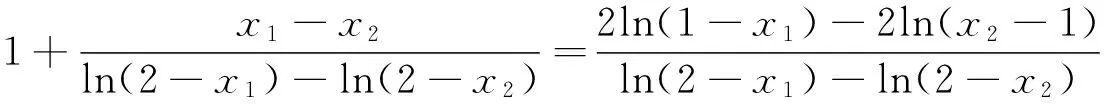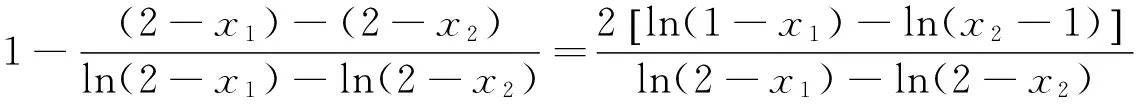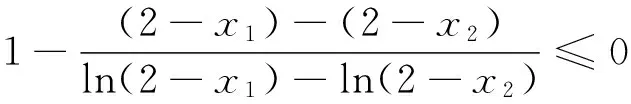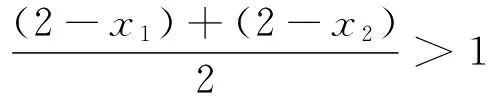消参思想在导数综合解答题中的应用探索

广东省兴宁市第一中学

蓝云波 何标宏 (邮编：514500)



解题方法

消参思想在导数综合解答题中的应用探索

广东省兴宁市第一中学

蓝云波 何标宏 (邮编：514500)

在各类考试中，含参数的导数解答题通常都作为压轴题的形式出现.这类考题由于含有参数，难度往往较大.因此，如何处理参数是解题的关键.笔者发现，对于含有参数问题的处理，大都是运用分类讨论的思想或分离参数的思想解答的.事实上，对于含有参数的问题，若能走出定势思维，把注意力转移到如何消去参数上，往往会有意想不到的效果和收获.通过一定的策略，把参数消去，化为不含参数的函数问题，问题往往便迎刃而解.下面笔者结合个人的教学实践，并以近年的高考题和模考题为例，谈谈消参思想在导数综合解答题中的应用.

1 利用放缩法

例1(2013年高考全国卷2理科)已知函数f(x)=ex-ln(x+m).

(1)设x=0是f(x)的极值点，求m,并讨论f(x)的单调性；

(2)当m≤2时，证明f(x)>0.

解析 (1)略；

综上所述，当m≤2时，证明f(x)>0.

例2 (2016年广东省广州市一模理科)已知函数f(x)=ex+m-x3,g(x)=ln(x+1)+2． (1)若曲线y=f(x)在点(0,f(0))处的切线斜率为1,求实数m的值；

(2)当m≥1时，证明：f(x)>g(x)-x3.

解析 (1)略；

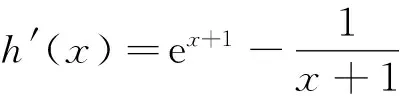
综上所述，当m≥1时，证明：f(x)>g(x)-x3.

点评 以上两题的函数中均含有参数m,若不消去参数，问题极为复杂.通过细致的观察，发现可利用放缩法，可把参数m消去，然后转化为不含参的具体函数.真可谓是“山穷水复疑无路，柳暗花明又一村”！最后通过导函数的单调性，结合零点存在定理，并利用虚拟设根，整体代换的思想实现问题的解决.

2 利用必要条件

例3 (2012年高考全国卷理科)设函数f(x)=ex-ax-2.

(1)求f(x)的单调区间；

(2)若a=1,k为整数，且当x>0时，(x-k)f′(x)+x+1>0,求k的最大值.

解析 (1)略；

(2)当a=1时，(x-k)f′(x)+x+1=(x-k)(ex-1)+x+1.

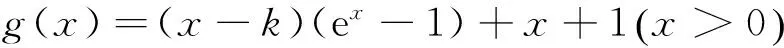
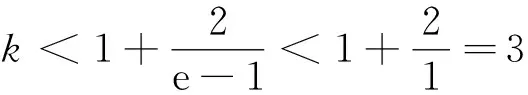
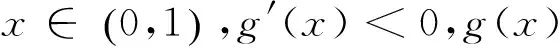
综上知整数k的最大值为2.

例4 (2015年北京市东城区示范校上学期综合能力测试)已知定义在(1,+)上的函数f(x)=x-lnx-2,g(x)=xlnx+x.

(1)求证：f(x)存在唯一的零点，且零点属于(3,4)；

(2)若k∈Z,且g(x)1恒成立，求k的最大值.

解析 (1)略；

(2)因为g(x)=xlnx+x,所以不等式g(x)k(x-1).要使g(x)1恒成立，则必须保证2ln2+2>k(2-1),所以k<2+2ln2<2+2lne=4.下面证明k=3时，不等式xlnx+x>3(x-1)成立.

设h(x)=xlnx+x-3(x-1)=xlnx-2x+3,x∈(1,+).

所以h′(x)=lnx-1,令h′(x)=0，得x=e.当x∈(1,e)时，h′(x)<0,当x∈(e,+)时，h′(x)>0,即h(x)在(1,e)上单调递减，在(e,+)上单调递增，所以当x=e时，函数h(x)有最小值，所以h(x)≥h(e)=elne-2e+3=3-e>0.所以xlnx+x>3(x-1)成立，

综上所述，整数k的最大值为3.

点评 例3和例4是经典的导数零点不可求问题，常规解法是用分类讨论思想与分离参数的思想解答的，但显得较为复杂.而本文给出的解法则通过必要条件缩小参数的范围，然后通过合理的估值，确定出参数的最大值，再做充分性证明.这样就达到了消去参数，化为不含参数的函数问题.通过这样的技术处理之后，例3就化为简单的问题，而例4则稍为复杂一些，但在通过运用常见的二次求导的思想方法后，最终实现了问题的圆满解决.

3 以极值点为主元，整体代换

例5 (2015年高考全国卷1文科)设函数f(x)=e2x-alnx.

(1)讨论f(x)的导函数f′(x)的零点个数；

因为g′(x)=2e2x+4xe2x>0,所以g(x)在(0,+)上单调递增，其值域为(-a,+).

当a≤0时，g(x)>0,所以f′(x)的零点个数为0；

当a>0时，g(x)的值域包含0,且g(x)单调递增，所以g(x)有唯一零点，所以f′(x)的零点个数为1.

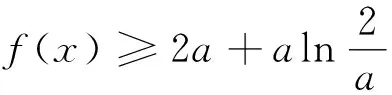
(1)当a=1时，讨论f(x)的单调性；

(2)当a>0时，设f(x)在x=x0处取得最小值，求证：f(x0)≤1.

解析 (1)略；

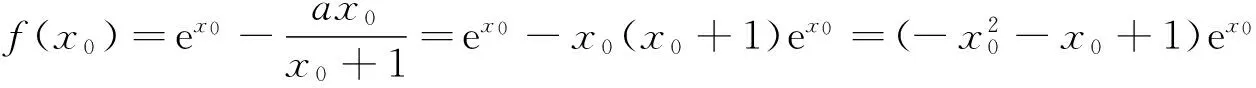
设g(x)=(-x2-x+1)ex(x>-1),则g′(x)=-x(x+3)ex.

令g′(x)>0,得-10.故g(x)在(-1,0)单调递增，(0,+)单调递减，g(x)≤g(0)=1,故f(x0)=g(x0)≤1.

点评 例5和例6通过虚拟设根，整体代换的思想，把参数消去.然后以极值点为主元，通过不等式的化简得到证明，或建立新的函数，求解函数的最值，最终实现问题的解决.整个过程行云流水，令人赏心悦目，不失为一种好的解法.

4 利用对数平均不等式

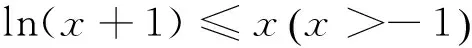
例7 (2015届江西省南昌市高三年级调研测试)已知f(x)=x-aex(a∈R,e为自然对数的底).

(1)讨论函数f(x)的单调性；

(2)若f(x)≤e2x对x∈R恒成立，求实数a的取值范围；

(3)若函数f(x)有两个不同的零点x1、x2,求证：x1+x2>2.

解析 (1)、(2)略；

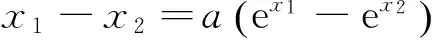
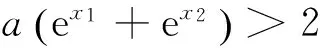
由对数平均不等式知，上式成立，所以x1+x2>2得证.

例8 (2016年高考全国卷1理科)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围；

(2)设x1、x2是f(x)的两个零点，证明：x1+x2<2.

解析 (1)略；

(2)由(1)知a>0,不妨设x1<1

两式相减得ln(2-x1)-ln(2-x2)+x1-x2=2ln(1-x1)-2ln(x2-1).

假设x1+x2≥2,则1-x1≤x2-1,所以ln(1-x1)≤ln(x2-1),

综上知x1+x2<2得证.

点评 例7和例8是极为重要的极值点偏移问题，这类问题与对数平均不等式问题越来越受到命题者的关注.通过探究发现，极值点偏移问题与对数平均不等式有深刻的内在联系.例7和例8官方给出的解答是利用极值点偏移的处理方法解答的，本文则从对数平均不等式这一视角实现问题的解决.这说明，数学思想的内在联系无处不在，让人叹为观止.

通过以上的探索，我们得到了四种常见的消去参数解答导数综合解答题的策略.这说明，走出思维的束缚，并合理使用数学思想，能实现方法的创新，而且这些方法如本文给出的这些创新解法往往也是一种通法，具有一定研究价值.更为重要的是，通过这样的探索，能开阔学生的视野，培养学生的创新性思维.教师在教学过程中，若能多做一些探究和反思，并合理选取学生较能接受的方法进行传授.可以达到提高数学教学的有效性的同时，也提高教师的教研水平和教学水平.

1 蓝云波.利用必要条件解题举隅.中学数学研究(广东)，2016(2)：4-6

2 蓝云波.奇思妙想速解几类典型的导数压轴题.中小学数学，2016(4)：47-49

3 蓝云波，何洪标.活跃在各类考试中的对数平均不等式.数学教学，2016(5)：22-25

4 邢友宝.极值点偏移问题的处理策略.中学数学教学参考(上旬)，2014(7)：19-22

2016-09-07)