椭圆曲线y2= px(x2- 64)的整数点

赵晶晶

（滇西科技师范学院 后勤管理处，云南 临沧 677000）

椭圆曲线y2= px(x2- 64)的整数点

赵晶晶

（滇西科技师范学院 后勤管理处，云南 临沧 677000）

设p为奇素数，主要利用同余和奇偶数的性质证明了椭圆曲线y2=px(x2-64)当p=17时有正整数点(x, y)=(9,51)，(17,255)；p≠17时至多有一组正整数点。

椭圆曲线；同余；正整数点

椭圆曲线的整数点是数论和算术代数几何学中基本而又重要的问题。关于椭圆曲线y2=ax(x2-b)的整数点问题，目前主要结论为：2007年，文[1]对b=1的情形进行了研究；2008年，文[2]对b=1的情形进行了研究；2012年，文[3]对b=1的情形进行了研究；2015年，文[4]对b=4的情形进行了研究。关于b=64的情形目前还未有相关结果，本文利用初等方法对p为奇素数时椭圆曲线y2=px(x2-64)的正整数点的情况进行了研究，得出了如下结论：

定理如果p为奇素数，则椭圆曲线

当p=17时有正整数点（x,y)=（9,51)，（17,255)；p≠17时至多有一组正整数点。

1 相关引理

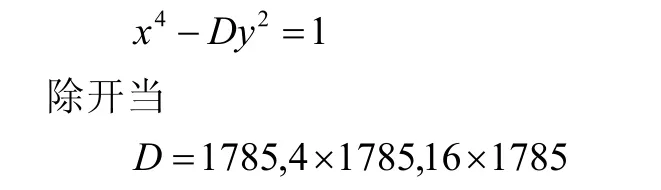
引理1[5]不定方程

分别有两组正整数解

外，最多只有一组正整数解(x,y)，且满足x2=x或11102x02-1，这里ε=x0+y0D 是Pell方程x2-Dy2=1的基本解。

引理2[6]设D1,D2是适合D1＞1的正整数，方程

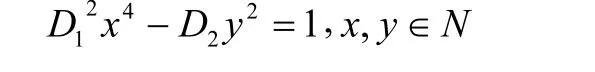
至多有一组解。

证明设(x,y)，x,y∈Z+是椭圆曲线(2)的正整数点，因为p是奇素数，故由(1)知p|y，设y=pz，z∈Z+，将其代入(1)，得

2 定理证明

因为gcd(x,x2-64)=gcd(x,64)=1或2或4或8或16或32或64，故(2)可分解为以下7种可能的情形：解得pa2=2，c=0。这与“c∈Z+”矛盾，故该情形椭圆曲线(1)无正整数点。

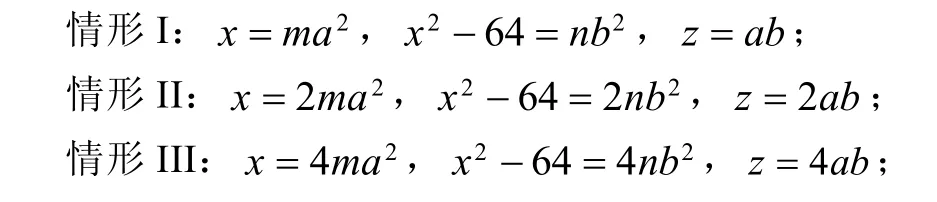
2.4 情形IV的讨论

2.4.1 当m=1，n=p时

由引理1知方程(11)至多有一组正整数解(a,c)，所以方程(2)至多有一组正整数解(x,z)，因此椭圆曲线(1)至多有一组正整数点。

2.4.2 当n=1，m=p时，

由引理2知方程(13)至多有一组正整数解(a,c)，因此方程(2)至多有一组正整数解(x,z)，因此椭圆曲线(1)至多有一组正整数点。

2.5 情形V的讨论

2.5.1 当m=1，n=p时

由引理2知方程(15)至多有一组正整数解(a,c)，因此方程(2)至多有一组正整数解(x,z)，因此椭圆曲线(1)至多有一组正整数点。

2.5.2 当n=1，m=p时

由(17)式知c为奇数，所以c2≡1(mod8)。因为b为偶数，而gcd(a,b)=1，所以a为奇数，则a4≡1(mod8)。又p为奇素数，则p2≡1(mod8)，故4p2a4≡4(mod8)。所以(17)式为

显然不成立，故该情形椭圆曲线(1)无正整数点。

2.6 情形VI的讨论

2.6.1 当m=1，n=p时

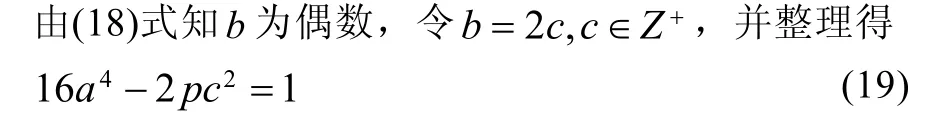
(19)式左边为偶数，右边为奇数，则(19)式不成立，故该情形椭圆曲线(1)无正整数点。

2.6.2 当n=1，m=p时

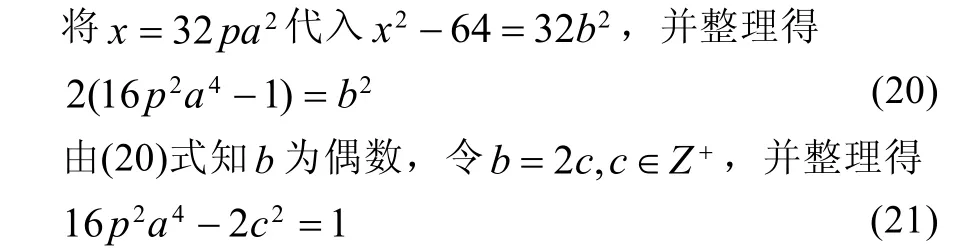
由引理2知方程(21)至多有一组正整数解(a,c)，因此方程(2)至多有一组正整数解(x,z)，因此椭圆曲线(1)至多有一组正整数点。

2.7 情形VII的讨论

2.7.1 当m=1，n=p时

由引理2知方程(22)至多有一组正整数解(a,b)，因此方程(2)至多有一组正整数解(x,z)，因此椭圆曲线(1)至多有一组正整数点。

2.7.2 当n=1，m=p时

这与“a，b∈Z+”矛盾，因此椭圆曲线(1)至多有一组正整数点。

综上定理得证。

[1] 祝辉林,陈建华.两个丢番图方程y2=nx(x2±1)[J].数学学报,2007,50(5):1071-1074.

[2] 乐茂华.椭圆曲线y2=px(x2±1)的正整数点[J].湛江师范学院学报,2008,29(3):1-2.

[3] 赵院娥.椭圆曲线y2=2px(x2-1)的正整数点的个数[J].西安石油大学学报,2012,27(2):106-107+110.

[4] 万飞.椭圆曲线y2=nx(x2-4)的整数点[J].湖北民族学院学报:自然科学版,2015,33(3):271-272.

[5] 孙琦,袁平之.关于不定方程x4-Dy2=1的一个注记[J].四川大学学报(自然科学版),1997,34(3):265-267.

[6] Bennett M A, Walsh G. the Diophantine equations b2X4-dY2=1[J]. Proc Amer Math Soc, 1999, 127(12): 3481-3491.

（责任编辑、校对：赵光峰）

The Positive Integral Points on the Elliptic Curve y2=px(x2-64)

ZHAO Jing-jing
(Department of Logistics Management, Dianxi Science and Technology Normal University, Lincang 677000, China)

Letpbe odd prime. Using some properties of congruence, odd number and even number, it was proved that if p=17, then the elliptic curve in title has just one positive integer point (9,51), (17,255); if p≠17, then the elliptic curve in title has at most one pair positive integer point.

elliptic curve; congruence; positive integer point

O156.1

A

1009-9115(2016)02-0017-03

10.3969/j.issn.1009-9115.2016.02.005

云南省教育厅科学研究项目（2014Y462）

2016-01-12

赵晶晶（1986-），女，彝族，云南临沧人，硕士研究生，助教，研究方向为数论及计算机应用技术。