基于ANFIS的麦蚜种群模型的建立与分析

田 洁,赵立纯,刘敬娜

(1.辽宁师范大学 数学学院,辽宁 大连 116029；2 鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

基于ANFIS的麦蚜种群模型的建立与分析

田 洁1，2,赵立纯1,2,刘敬娜1

(1.辽宁师范大学 数学学院,辽宁 大连 116029；2 鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

基于不同温度和大麦种群不同生长阶段(软组织、叶片发育阶段等)的麦蚜种群实验数据，首先利用自适应神经模糊推理系统(ANFIS)，分别建立高斯型、三角型和梯型隶属度函数的麦蚜种群内禀增长率的T-S初始模糊模型．然后在误差允许范围内，应用ANFIS具体训练流程对相应初始模型进行修正，并通过误差选择与原始数据拟合程度最好的模型,最后利用数值模拟验证结论的正确性．

麦蚜种群系统；ANFIS；隶属度函数；误差分析

利用传统数学的精确性，电子计算机能在几小时内将圆周率计算到小数点后几万位；火箭发射之前，通过计算能精确预测它的飞行轨道和着陆地点等．但是，客观世界还存在着另一种现象，如人们说这块试验田的麦子长得“好”，那块试验田的麦子长得“不好”，那么“好”与“不好”的界限是什么? 人们用传统的数学方法难以给出它们的具体界限，实际上这就是人们所说的模糊性．而美国科学家查德教授早在上世纪60年代就已意识到这种传统数学的局限性，并指出：“如果深入研究人类的认识过程，我们将发现人们能运用模糊概念是一个巨大的财富而不是包袱，这一点是理解人类智能和机器智能之间深奥区别的关键”，他还在论文《Fuzz Sets》中，首次把模糊性和数学统一在一起，形成了模糊数学这门学科[1]．模糊数学是研究模糊性现象的数学，是处理非线性系统的有效工具，它把非线性系统分解成无穷个线性系统，然后用权重把各个线性系统连接起来，也就是说总体是非线性的但局部是线性的，它在自然科学、工程技术等领域有着广泛的应用[2～4]．近10年来，考虑到大多数生物系统的非线性性,一些学者将模糊思想应用到生物系统的研究中,如JI Horiuchi以微生物连续培养为背景，应用两种不同的控制手段(即经典的PID控制和模糊控制)分别实施模拟控制，结果发现：后者比前者更能达到控制标准[5]．张庆灵等人利用T-S模糊广义系统理论研究了一类具有脉冲行为生物经济系统的奇异诱导分岔及其控制问题，对具有脉冲行为的不平衡经济系统，建立T-S模糊广义系统并设计反馈控制器，使系统达到某种意义下的平衡状态[6]．Magda等人以柑橘栽培为背景，基于模糊规则建立捕食者-被捕食者模型，来研究瓢虫与蚜虫之间的捕食与被捕食关系，并通过施加模糊控制来控制蚜虫种群密度以达到预期状态[7].Bor-Sen Chen和Chih-Hung Wu结合T-S模糊理论和鲁棒最优参考跟踪方法，对随机合成生物系统进行设计和分析，针对基因网络内在参数波动，未知分子与外环境干扰等因素，利用T-S模糊方法设计基因振荡器，实现鲁棒最优参考输出跟踪[8]．闻飞翔等以温室草莓为研究背景，基于生物种群的Logistic增长模型，结合灰霉病病菌所具有的模糊性，建立温室草莓灰霉病病菌的T-S模糊模型，根据Lyapunov稳定性定理，给出所建T-S模糊控制系统稳定的条件，并设计控制器，使模型全局稳定，为温室草莓灰霉病的预防与控制提供理论依据[9]．上述文献说明模糊数学已在生物学研究方面得到了一些应用，从建模方法上看它们多集中在T-S模糊模型方面，其优点是：可用线性系统以任意精度逼近复杂的生物系统，并用成熟的线性系统理论分析该生物系统，但其结构和参数却很难辨识[10]．然而，由Jyh-Shing Roger Jang在1993年提出的自适应神经模糊推理系统(ANFIS)可以解决这一问题，自适应神经模糊推理系统(ANFIS)是一种将模糊逻辑推理和神经网络相结合的复合系统，一方面，模糊逻辑推理系统可广泛用于模糊控制，巧妙地引入了“隶属度”概念，使规则数值化，从而能很好地处理结构化的知识；另一方面，神经网络具有较强的自适应性和学习能力，克服了传统模糊推理系统学习能力差的缺点，对辨识模型的结构和参数有很大的帮助[11～13]．ANFIS在工程技术方面已得到广泛的应用，在社会系统中也有一些应用[14,15]，但在生态系统方面的应用却很少，有鉴于此，本文基于文献[16]的实验数据，应用ANFIS方法建立基于不同隶属度函数的麦蚜种群内禀增长率模型，通过比较分析制定ANFIS训练流程图，确定与实验数据相匹配的最佳模型.

1 ANFIS设计

根据文献[16]的实验数据，以温度和大麦种群不同生长阶段(软组织、叶片发育阶段等)为输入变量，以麦蚜种群内禀增长率为输出变量，利用自适应神经模糊推理系统(ANFIS)，按照输入实验数据，生成初始FIS，数据训练，并根据训练后数据建立麦蚜种群的T-S模糊模型，具体过程如下：

1.1 输入实验数据

将文献[16]中在不同温度(t)和大麦种群不同生长阶段(软组织、叶片发育阶段等)(s)的麦蚜种群实验数据作为实测数据装入ANFIS；在实测数据中将序号为偶数(奇数)的数据作为测试数据，装入ANFIS编辑器.

1.2 生成初始FIS

依据数据的分布情况，拟确定模糊规则个数(假设模糊规则个数为6)，生成初始FIS;选择3类隶属度函数，即高斯型、三角型、梯型，建立3类模型．

1.3 数据训练

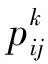
注1:实际训练时采用人为指定的方法来生成训练结构，其中，训练次数为50次,训练步长为0.01；学习时采用“hybrid”混合学习算法.

值得注意的是训练前后隶属度函数的类型不变，只是参数发生了变化.

1.4 模型建立

根据上述过程的数据训练结果可以写出如下3类模型:

1.4.1 基于高斯型隶属度函数的模型 经过训练得模糊规则如下：

规则1：if t is t1and s is s1then r1=-0.055 79 t+0.058 09 s-1.43；

规则2：if t is t2and s is s2then r2=-0.419 t-0.008 365 s+1.539；

规则3：if t is t3and s is s3then r3=-0.015 42 t+0.048 38 s-3.795；

规则4：if t is t4and s is s4then r4=-0.172 t+0.026 17 s+4.864；

规则5：if t is t5and s is s5then r5=-0.144 6 t+0.033 85 s+2.542；

规则6：if t is t6and s is s6then r6=-0.011 57 t+0.000 943 3 s-0.001 437．

其中，ti，si，i=1，2，3，4，5，6.为相应模糊子集的隶属度函数，具体表示如下：

由单点模糊化、乘积推理和平均加权反模糊化,可得模糊系统的状态方程如下：

r=μ1r1+μ2r2+μ3r3+μ4r4+μ5r5+μ6r6,

(1)

其中,

1.4.2 基于三角型隶属度函数的模型 经过训练得模糊规则如下：

规则1：if t is t1and s is s1then r1=-0.02119t+0.01384s-10.1405；

规则2：if t is t2and s is s2then r2=-0.02527t-0.001148s+0.08379；

规则3：if t is t3and s is s3then r3=-0.01585t+0.007375s-0.2108；

规则4：if t is t4and s is s4then r4=-0.03295t+0.001574s+1.26；

规则5：if t is t5and s is s5then r5=0.01282t+0.002349s+0.08503；

规则6：if t is t6and s is s6then r6=-0.0093t-0.0001454s+0.08433．

其中，ti，si，i=1，2，3，4，5，6.为相应模糊子集的隶属度函数,具体如下：

模糊系统的整个状态方程建模同模型(1)．

1.4.3 基于梯型隶属度函数的模型 经过训练得模糊规则如下：

规则1：if t is t1and s is s1then r1=-0.01975t+0.02471s-0.6128；

规则2：if t is t2and s is s2then r2=-0.1835t-0.003593s+1.156；

规则3：if t is t3and s is s3then r3=-0.01577t+0.0227s-1.514；

规则4：if t is t4and s is s4then r4=0.2535t+0.008627s-5.98；

规则5：if t is t5and s is s5then r5=0.3159t+0.006425s-4.18；

规则6：if t is t6and s is s6then r6=-0.0712t-0.0001281s+0.3969.

其中，ti，si，i=1，2，3，4，5，6.为相应模糊子集的隶属度函数，具体如下：

模糊系统的整个状态方程建模同模型(1)．

2 误差分析

基于不同的隶属度函数类型,根据上述过程分别就模糊规则为4、6和9的情况对模型进行分析，以研究模糊规则个数和模糊隶属度函数类型对模型误差的影响．为此分别用yk和yEK表示实际输出和期望输出，设模型误差估计式为

(2)

注2：表1中规则个数为4，并采用梯型隶属度函数时，ANFIS不能直接给出模型误差，出现此错误的原因是数据的数量小于可修改的参数的数量.一般情况下具有两类处理办法：一是增加训练数据；二是在数据训练之前选用高斯型隶属度函数，数据训练后再重新选用梯型隶属度函数[19]．

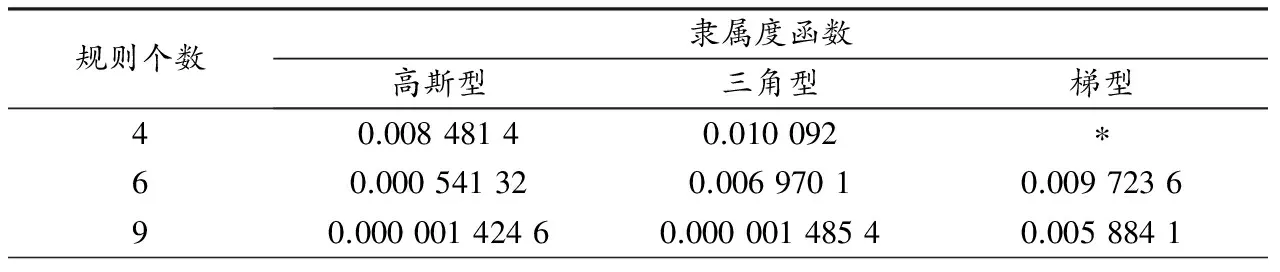
表1 模型误差

从表1可以看到，所建模型的精确性受规则个数与隶属度函数类型的影响：一方面，同一规则个数，所对应隶属度函数类型不同，则模型的误差亦不同，如对本文数据而言，当规则个数分别为4、6和9时，采用高斯型隶属度函数获得的模型的误差E最小；另一方面，同一隶属度函数类型，所对应规则个数不同，则模型的误差亦不同，如对本文数据而言，当采用高斯型、三角型和梯型隶属度函时，规则个数为9时获得的模型的误差E最小．相应的模拟结果见图1～3．

图1 规则个数为4的误差模拟图

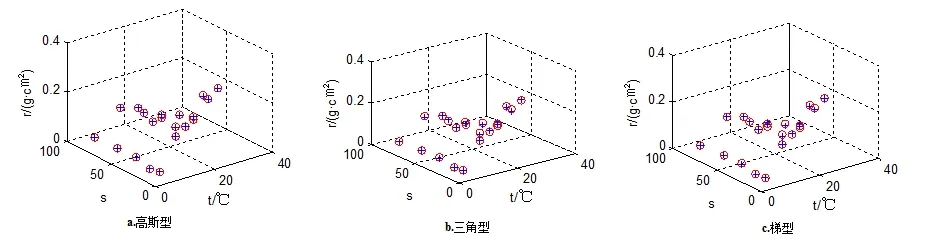
图2 规则个数为6的误差模拟图

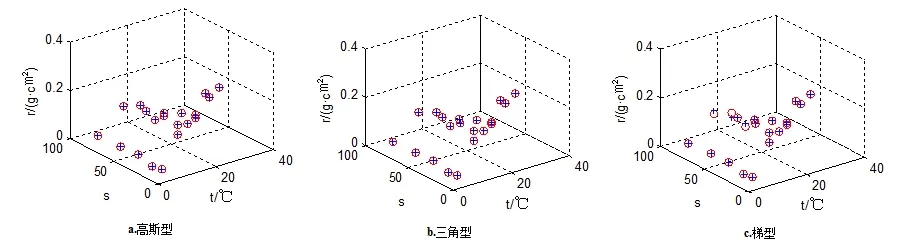
图3 规则个数为9的误差模拟图

注 3：图1(c)中梯型为训练前隶属函数类型为高斯型，训练后隶属度类型为梯型所画图像．

注4：○代表原始数据,+代表训练后数据，图中⊕越多说明原始数据与训练后数据拟合越好．

根据上述误差分析结果来看，虽然隶属度函数类型和规则个数直接影响模型的误差，但是这种影响没有明显规律，并且在实际应用中选取多个规则未必是件好事，因为规则个数大将增加学习量．有鉴于此，我们在随后部分设计了ANFIS训练流程，建立最佳模型．

3 ANFIS训练流程

根据生态学含义，给出模型的允许误差范围，基于ANFIS建立麦蚜种群内禀增长率的T-S模糊模型具体步骤：

第1步：依据数据的分布情况，对数据进行分析，例如聚类分析等，拟确定模糊规则个数；

第2步：针对不同隶属度函数类型，利用麦蚜种群实验数据建立相应的T-S模糊模型；

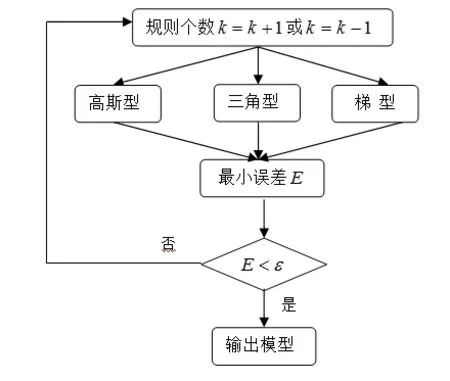
图4 ANFIS训练流程图

第3步：选出训练后各隶属函数下模型输出的最小误差；

第4步：判断误差是否在允许的范围内，若在要求范围内，接第五步完成模型建立；若不在要求范围内，则增加模糊规则个数后重新返回第一步进入第二次循环；

第5步：输出结果(具体流程图见图4)．

根据上述ANFIS训练流程图建立的模糊系统的模型可以比较准确地刻画麦蚜种群的内禀增长率，为蚜虫种群的预防和控制提供理论支持.

[1] 吴可.模糊数学的产生、发展和应用[J].科技信息:科学教研,2007(29):215-215.

[2] 孙兆刚.模糊数学的产生及其哲学意蕴[D].武汉:武汉理工大学,2003.

[3] 袁学海.基于Zadeh蕴涵的重心法模糊系统[J].辽宁师范大学学报：自然科学版,2012(4):433-440.

[4] 许士国,陈守煜.模糊数学在工程技术领域中的方法论作用[J].大连理工大学学报,1991(6):693-698.

[5] Horiuchi J I.Fuzzy modeling and control of biological processes[J].Journal of Bioscience & Bioengineering,2002,94(94):574-578.

[6] 张悦，张庆灵，赵立纯.一类生物经济系统的分析与控制[J].控制工程，2007，14(6)：599-602.

[7] Peixoto M D S,Barros L C D,Bassanezi R C.Predator-prey fuzzy model[J].Ecological Modelling,2008,214(1):39-44.

[8] CHEN Bor-Sen,WU Chih-Hung.Robust Opitimal Reference-Tracking Design Method for Stochastic Synthetic Biology Systems:T-S Fuzzy Approach[J].IEEE,2010:1144-1150.

[9] 闻飞祥,赵立纯,刘敬娜,等.温室草莓灰霉病T-S模糊控制模型[J].辽宁科技大学学报,2015,38(4):311-314.

[10] 蔡卫菊,张颖超.基于T-S模糊模型的神经网络的系统辨识[J].微计算机信息,2006,22(2):176-178.

[11] 侯志祥,申群太,李河清.基于自适应神经模糊推理系统的非线性系统辨识[J].系统工程与电子技术,2005,27(1):108-110.

[12] 田禹,张帅,陈琳，等.应用 ANFIS 预测蠕虫反应器的污泥减量速率并优化其运行条件[J].环境科学学报,2013,33(2):464-472.

[13] 张浩炯,余岳峰,王强.应用自适应神经模糊推理系统(ANFS)进行建模与仿真[J].计算机仿真,2002,19(4):47-49.

[14] Yousif,Al-Mashhadany.High-Performance of Power System Based upon ANFIS (Adaptive Neuro-Fuzzy Inference System) Controller[J].能源与动力工程，2014(4):729-734.

[15] 夏海波,张蒙蒙,胡甚平,等.船舶安全航行系统风险分级ANFIS模型[J].上海海事大学学报,2014,35(2):17-21.

[16] Matis.Life tables and demographic statistics of Russian wheat aphid (Hemiptera:Aphididae) reared at different temperatures and on different host plant growth stages[J].Entomol，2009，106:205-210.

[17] 王士同.模糊系统、模糊神经网络及应用程序设计[M].上海:上海科学技术文献出版社,1998.

[18] 张嗣瀛,高立群.现代控制理论[M].北京:清华大学出版社,2006.

[19] 石辛民.模糊控制及其MATLAB仿真[M].北京：清华大学出版社,2008.

(责任编辑：张冬冬)

The modeling and analysis of the wheat aphid population based on ANFIS

TIAN Jie1,2，ZHAO Lichun1，2，LIU Jingna1

(1.CollegeofMathematics,LiaoningNormalUniversity,Dalian,Liaoning,116029,China; 2.SchoolofMathematicsandInformationScience，AnshanNormalUniversity,AnshanLiaoning114007,China)

Bases on experimental data of the wheat aphid population in different temperatures and different growth stages(soft tissue，leaf development stage etc)，firstly，some initial models of intrinsic growth rate of aphid population with three membership functions are proposed by adaptive neural-network based fuzzy interference system(ANFIS)，respectively.Secondly，for a given error，the corresponding models are modified using specific training processes of ANFIS，and the model which fits the date better than other models is chosen from the initial models above．Finally，the simulations are carried out to prove the result of the paper．

wheat aphid population；ANFIS；membership functions；error analysis

2016-06-10

国家自然科学基金项目(60974004);辽宁省教育厅项目(L2014454).

田洁(1993-)，女，辽宁铁岭人，辽宁师范大学数学学院硕士生．

O29

A

1008-2441(2016)06-0006-06