毒素具脉冲扩散与输入的单种群动力学模型
刘兰兰,焦建军,2
(1.贵州财经大学 数学与统计学院,贵州 贵阳 550004;2.贵州财经大学 贵州省经济系统仿真重点实验室,贵州 贵阳 550004)
毒素具脉冲扩散与输入的单种群动力学模型
刘兰兰1,焦建军1,2
(1.贵州财经大学 数学与统计学院,贵州 贵阳 550004;2.贵州财经大学 贵州省经济系统仿真重点实验室,贵州 贵阳 550004)
建立了毒素具脉冲扩散与输入的单种群动力学模型,利用脉冲微分方程理论对模型进行研究,分别获得了系统种群灭绝和持久生存的条件,为环境污染中的生物资源管理提供了可靠的依据.
脉冲输入环境毒素;脉冲扩散;单种群动力学模型
环境污染正在威胁物种的持续生存.近年来,有许多学者研究了污染环境下的单种群动力学模型[1~5],文献[1][6]采用数学建模的方法研究了环境污染给生物种群生存带来的影响,其中大多数研究都假设毒素是连续输入的.事实上,毒素通常是以脉冲的方式释放到环境中[7].最近,脉冲微分方程理论被引用到种群的动态研究中[8~11].本文考虑毒素的脉冲扩散与输入对单种群物种的影响,建立了相应的数学模型,利用脉冲微分方程理论对模型进行分析并得到有意义的结论.
1 模型的建立
考虑种群具有Logistic增长的微分方程模型为
(1)
其中,x(t)为种群在t时刻的密度,a>0为种群的内禀增长率,b>0为种群的种内竞争系数.如果考虑到种群的脉冲收获,那么式(1)可改进为式(2),其中,x(t)为种群在t时刻的密度,a>0为种群的内禀增长率,b>0为种群的种内竞争系数,μ为种群的脉冲收获系数,τ为种群的脉冲出生周期.
(2)
基于上述讨论,考虑毒素具脉冲扩散与输入对单种群生存的影响,本文建立以下模型:
(3)
其中,系统(3)由2个环境组成,x(t)表示种群在t时刻的密度,且种群x(t)生活在环境1中;ce1(t)表示环境1中的毒素在时刻t的浓度;ce2(t)表示环境2中的毒素在时刻t的浓度;a>0表示种群的内禀增长率;b>0表示种群的种内竞争系数;β 表示环境1中的毒素对种群的损耗率系数;-h1ce1(t)表示环境1中的毒素在时刻t损耗总量;-h2ce2(t)表示环境2中的毒素在时刻t损耗总量;毒素损耗主要有生态环境中的生物转化、水解、分解,微生物分解和光合作用分解等;μ表示 t=nτ(n∈Z+) 时环境1的种群因为脉冲输入毒素对种群的损耗系数;μ1表示 t=nτ(n∈Z+) 时环境1毒素浓度的脉冲输入;μ2表示t=nτ(n∈Z+)时环境2中毒素浓度的脉冲输入;0 lim(t,u)→((n+1)τ+,z)V(t,u)=V((n+1)τ+),z) 存在; ii)V在z是局部李普希茨的. 讨论主要结果前,首先给出引理.根据文献[12]容易得到: 引理1 系统(3)的解(x(t),ce1(t),ce2(t))是最终一致有界的,即存在常数M>0,使得当t充分大时, 考虑系统(3)的子系统 (4) 于是得到 (5) 证明 为了方便,做记号 那么差分方程(5)线性化后可以写成 (7) 1-trM+detM>0, 显然 那么 1-trM+detM= 1-[(1-D)e-h1τ+(1-D)e-h2τ]+[(1-D)e-h1τ×(1-D)e-h2τ-De-h1τ×De-h2τ]= [1-(1-D)e-h1τ]×[1-(1-D)e-h2τ]-De-h1τ×De-h2τ= (1-e-h1τ)(1-e-h2τ)+De-h2τ(1-e-h1τ)+De-h1τ(1-e-h2τ)>0, 由引理2可知: 由此得到系统(3)的另外一个子系统为: (8) 得到频闪映射 (9) (10) 于是,容易得到: 引理3 引理4 (11) 由系统(3)的第一个方程可知 (12) 于是得到: (13) 那么(13)的比较微分方程 (14) 类似引理4得到: 定理1 (15) 综合引理4和定理1可得: 定理2 根据实际的生物资源管理,本文结合脉冲微分方程理论,讨论了毒素具脉冲扩散与输入的单种群动力学模型,得出了生物资源管理中生物种群生存情况的控制阈值,这个结论对于生物资源管理是非常有意义的,如果其它的系数是确定的,那么 是控制阈值,当μ>μ*,物种将灭绝;当μ<μ*,物种将持久存在. [1] Hallam T G,Clark C E,Jordan G S.Effects of toxicants on population:a qualitative approach I.equilibrium environmental exposure [J].Ecological Modelling,1983,18(3/4):291-340. [2] Debasis M.Persistence and global stability of a population in a polluted environment with delay[J].Journal of Biological Systems,2002,10:225-232. [3] Jiao Jianjun,Long Wen,Chen Lansun.A single stages-structured population model with mature individuals in a polluted environment and pulse input of environmental toxin[J].Nonlinear Analysis:Real World Applicationgs,2009,10(5):3073-3081. [4] 焦建军,鲍磊,陈兰荪.具脉冲出生与脉冲收获阶段结构单独种群动力学模型[J].吉林大学学报:理学版,2011,49(1):6-10. [5] 栾施,刘兵,张丽霞.一个污染环境中的单种群模型的动力学性质[J].生物数学学报,2011,26(4):689-694. [6] Zhang B G.Population’s Ecological Mathematics Modeling[M].Qingdao:Publishing of Qingdao Merine University,1990. [7] Liu B,Chen L S,Zhang Y J.The effects of impulsive toxicant anput on a population in a polluted environment[J].J Biol Syst,2003(11):265-287. [8] Liu X N.Impulsive stabilization and applications to population growth models[J].I Math,1995,5(1):381-385. [9] Lakshmikantham V,Bainov DD,Simeonov PS.Theory of impulsive differential equations[M].Singapore:World Scientific,1989. [10] Song X Y,Chen L S.Uniform persistence and global attractivity for nonautonomous competitive systems with dispersion[J].I Syst Sci Complex,2002(15):307-314. [11] Jiao Jianjun,Chen Lansun,Luo Guilie.An appropriate pest management SI model with biological and chemical control concern[J].Applied Mathematics and Computation,2008(196):285-287. [12] 焦建军,文乾英.具脉冲出生与脉冲输入环境毒素的单种群动力学模型研究[J].数学的实践与认识,2014(22):299-304. (责任编辑:张冬冬) A single population dynamics model with pulse input and spread of environmental toxin LIU Lanlan1,JIAO Jianjun1,2 (1.SchoolofMathematicsandStatistics,GuizhouUniversityofFinance&Economics,GuizhouGuiyang550004,China;2.GuizhouKeyLaboratoryofEconomicsSystemSimulation,GuizhouUniversityofFinance&Economics,GuizhouGuiyang550004,China) This paper forms a single population dynamics model with pulse input and spread of Environmental toxin,using the theory of impulsive differential equations to solve the model and get the final conclusion.Conditions are obtained for the species extinction and persistent systems.It provides reliable strategies for the biological resources management of the environmental pollution. single population dynamics model;pulse input of environmental toxin;pulse spread 2016-10-20 国家自然科学基金资助(11361014). 刘兰兰(1994-),女,贵州贵阳人,贵州财经大学数学与统计学院硕士生. O175.4 A 1008-2441(2016)06-0001-052 动力学分析
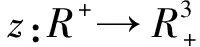

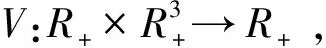

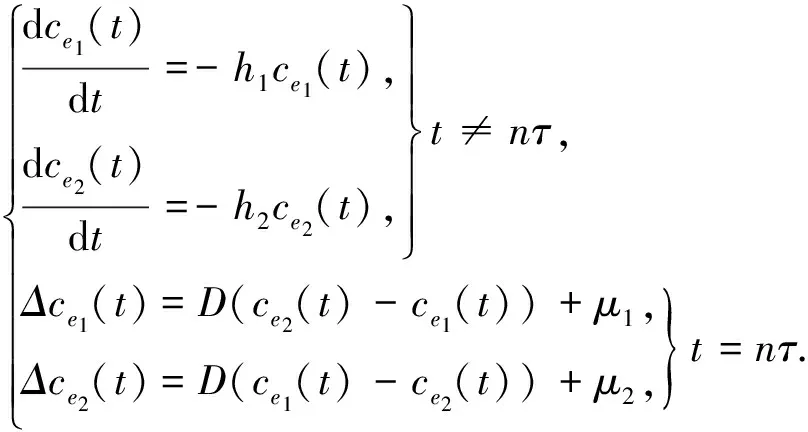
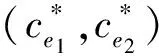
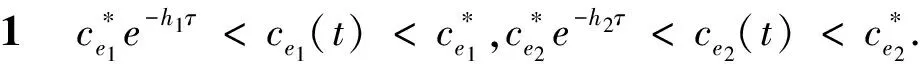
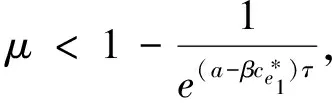
3 主要结论

