混沌振子检测微弱信号的抗噪声能力研究

刘 燕 张翠侠 张明玉

（宿州学院，安徽 宿州 234002）

混沌振子检测微弱信号的抗噪声能力研究

刘 燕 张翠侠 张明玉

（宿州学院，安徽 宿州 234002）

使用混沌振子检测微弱信号时,只要把含有已知频率的待测信号加入一个对应于此频率的、处于混沌临界状态的混沌系统中，该混沌系统的动力学行为就会发生很大变化，以此来判断微弱信号的存在。往往输入信号和噪声同时作用于混沌系统，这就要求噪声不能引起混沌系统状态的改变。在此基础上，重点从理论和数值仿真分析了噪声对混沌振子系统状态的影响。并提出了基于自相关方法和混沌系统相结合检测微弱信号的新方法。

微弱信号；混沌振子；随机噪声；自相关方法

故障发生的早期，信号本身比较微弱，如果有噪声的存在，更难提取特征信号。很多学者致力于小波消噪[1,2]、 Winger-Ville分布[3]， EMD[4,5]等方法的研究，如果采用上述线性信号分析方法进行早期故障诊断，非线性成分减少，不能够真实反映非线性振动的特质。混沌振子理论针对非线性信号检测提供了一种新的提取方法，文献[6]提出了一种基于混沌振子和局域波的微弱信号检测方法，并成功的提取转子系统早期的故障信息。文献[7]提出了基于经验模态分解(EMD)和Duffing振子相结合的诊断方法，利用该方法能成功的检测齿轮箱轴承故障。使用混沌振子来检测微弱信号时,只要把同样频率的微弱信号作用于处于混沌临界状态的混沌系统中，该混沌系统的动力学行为可由混沌临界状态转变成大尺度周期状态，以此来检测微弱信号。往往信号和噪声是同时存在的，而噪声又是随机产生的，因此是否引起混沌振子的动力学行为发生改变决定了该检测方法的准确性，目前还没有文献给出确定的结论。本文分别从数学模型和数值仿真两方面研究噪声对混沌振子系统临界状态的影响。并将传统的时域检测自相关方法结合混沌振子检测微弱信号，有效的提高了信噪比。

1. 混沌振子的动力学形态

混沌振子检测模型是通过Homels型Duffing方程[8]建立的，方程形式如下：

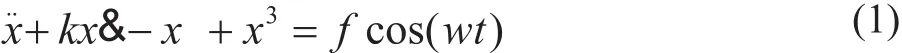
其中k为阻尼比，取k=0.5；-x+x3为非线性恢复力；fcos(wt)为内置信号。

令 t=ω0τ，并且当外部周期信号加入时，式(1)变为

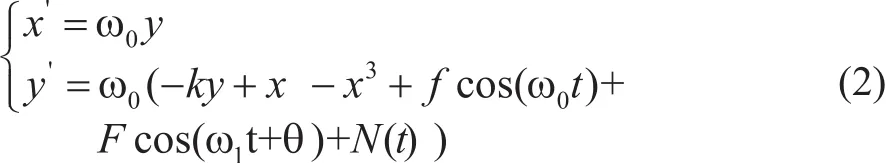
式中：ω0为内置信号摄动力的频率, ω1为被测周期信号的频率，θ为被测周期信号的相位，N(t)为均值为0的随机噪声。

2. 噪声对混沌振子状态的影响

2.1 理论状态下噪声对Duffing振子混沌状态的影响

假设方程（1）在混沌临界状态下解为x(t)，当加入均值为零、方差为σ2的白噪声n(t)时，对解x(t)的扰动用 表示，那么式（1）表示为：

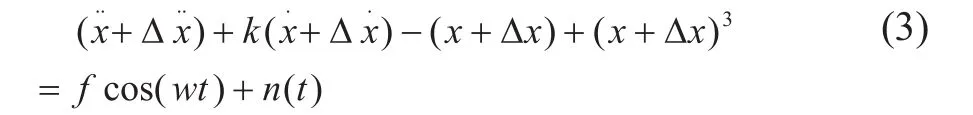
式(3)减去(1)式得：

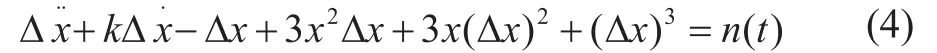
由于Δx很小，略去Δx的高阶项，令c(t)=1-3x2(t)可得:

将式(6)写成矢量微分方程的形式

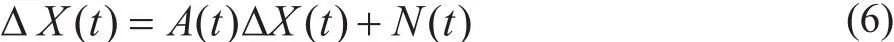
式中

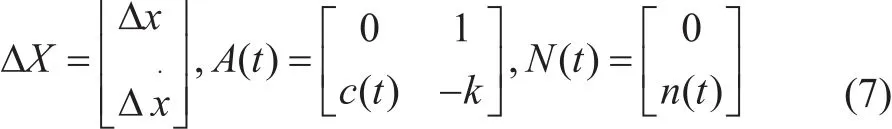
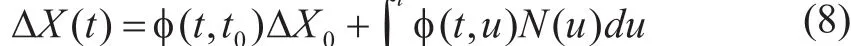
式中，Φ是系统的状态转移矩阵，

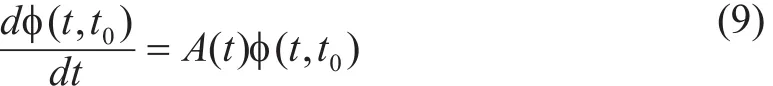
为方程的零输入解，将快速衰减为零。此时只考虑稳态时的特性，式(9)变成

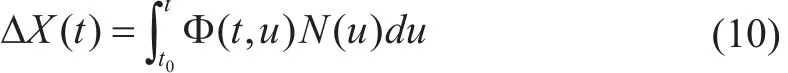
均值

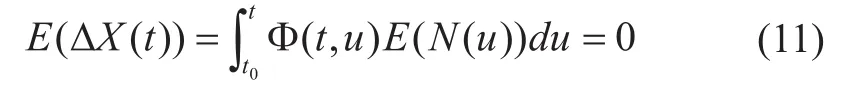
方差矩阵为

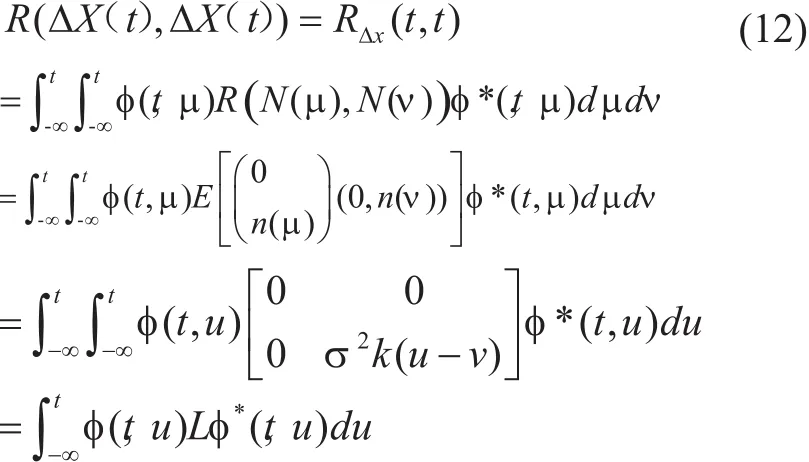
此时

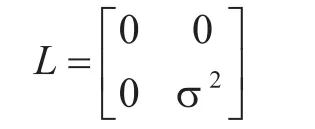
通过分析可知，随意分布的零均值噪声不能使系统的原有运动轨迹发生变化，只将外围轨道变的粗燥，当演化时间趋于无限长时，混沌系统对噪声有一定的免疫力。而在我们实际检测中，演化时间是有具体的数字的，所以，噪声还是会对混沌系统产生一定影响，但总的来说，混沌系统已对噪声信号体现出十分强的免疫力。

2.2 仿真研究噪声对混沌振子系统临界状态的影响

通过改变白噪声的强度来研究对Duffing振子临界状态的影响，结果如下表所示（表1）。采用计算步长h =0.02，数据长度n=9126，ω0=2×π×100，对式(2)进行离散化并采用4阶Runge-Kutta法进行求解，计算得到混沌振子阈值fb=0.5665。

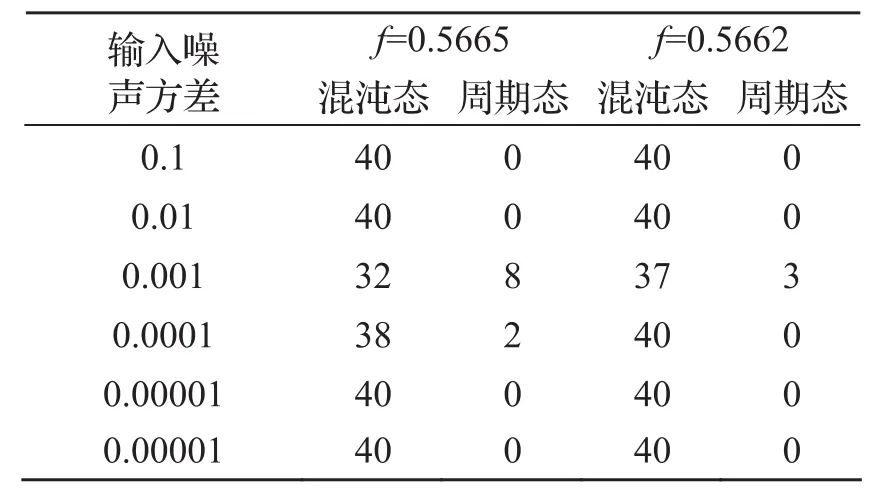
表1 噪声对不同策动力值混沌阵子的影响a

从表1可以看出，噪声方差不同，系统输出可能是混沌状态也可能是大尺度周期状态，系统的状态不确定，噪声有可能引起系统的动力学行为发生变化。从f=0.5665和f=0.5662的数据发现，驱动值不一样，系统的抗噪声能力也不同，驱动力幅值越接近系统的临界阈值，对噪声越敏感。这是由于系统本身处于混沌很深的状态，噪声很难引起系统状态的改变。从表1可以看出，数值仿真结果和理论结果有微小的差距，当用数学方程分析噪声对混沌振子状态的影响时，很多客观因素考虑的不是很全面，致使结果不够精确，总体来说，混沌振子系统对噪声表现了很强的免疫力。

3. 混沌振子抗噪声的能力

混沌振子对噪声有极强的免疫力，但是混沌系统能够接受最低信噪比是多少呢?下面通过仿真来分析。

取待测信号为：

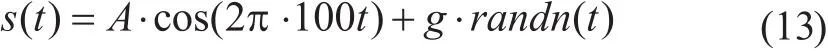
式中：A为信号幅值；g为均值为0的高斯白噪声方差。

将(13)带入式(1)得：

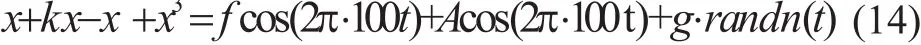
当k=0.5,ω0=2×π×100rad/s,计算步长h=0.02, n=9126，计算得到混沌振子阈值fb=0.5665。令f=0.56 ，A=0.04，f +A ＞ fb 。当噪声强度g=0时，振子相图状态是大尺度周期状态，分别取噪声强度g=0.6、0.7、0.8、0.9，观察相图的变化，结果如图1所示。

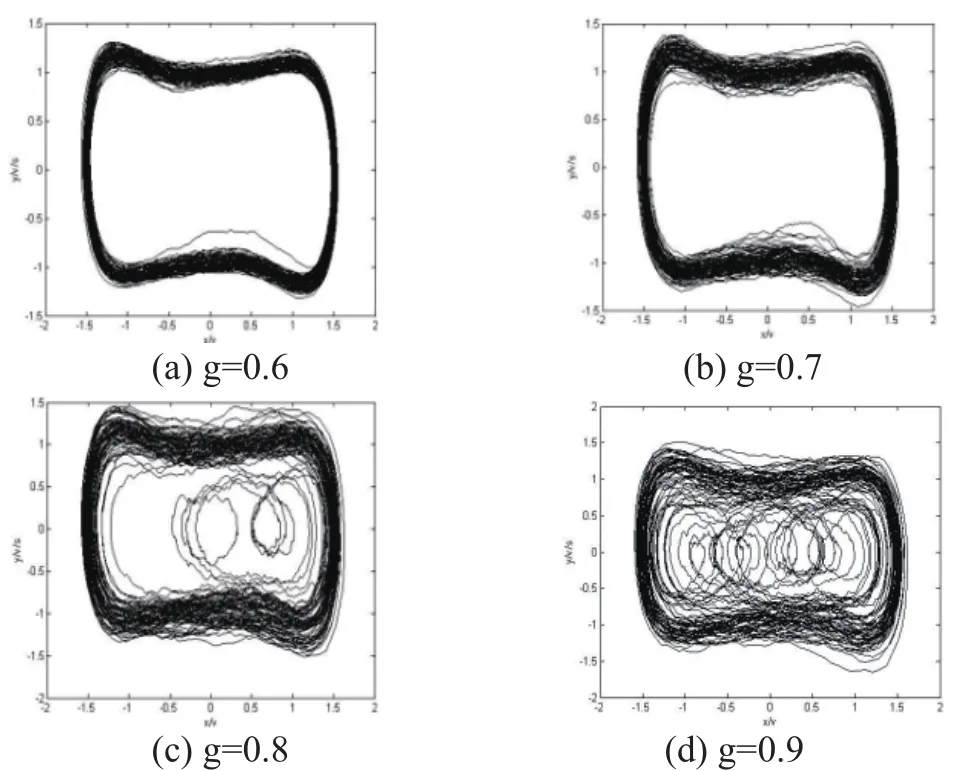
图1 不同噪声强度下的混沌振子相图

由图1(a)和(b)图可知，相图仍然处于大尺度周期状态，继续增加噪声强度，由图(d)可知，相图状态发生很大的改变，振子由大尺度周期状态转变到混沌状态，此时无法正确检测微弱信号。

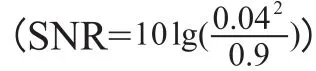
4. 自相关方法与混沌振子相结合检测微弱信号

对于给定的信号，任何时刻的取值都具有很高的相关性，而对于随机噪声，相关性就比较差。自相关就是利用噪声与噪声、噪声与信号之间的相关性比较差来提高信号的信噪比的。假设待检测信号表示为：

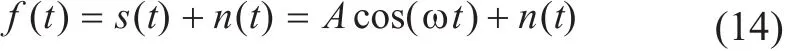
则f(t)自相关函数为

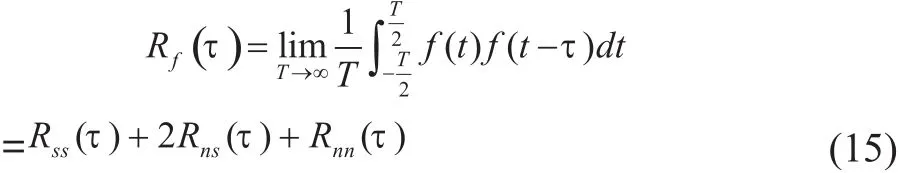
其中：Rss(τ)为s(t)与s(t)自相关函数，Rns( τ)是n(t)与s(t)的自相关函数，Rnn(τ)是n(t)与n(t)的自相关函数。由于周期信号s(t)与随机噪声n(t)毫无关联，其互相关函数为零，故

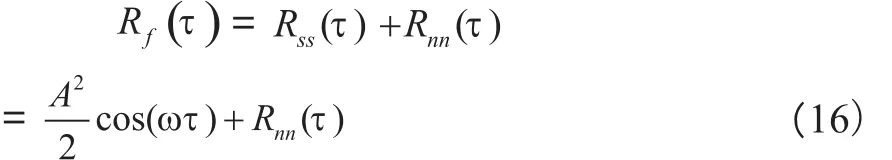
式中: τ为时移,上式中只要积分时间很长，Rnn( τ)就会衰减很快。但是工程实际中，积分时间不可能很长，所以还是会残留一定量噪声的。因此，由式(16)可知，将含噪信号经过自相关计算，输入信号的频率并没有改变，只是信噪比提高了。信号的检测流程如图2所示。

图2 检测框图

仿真分析：将没有经过自相关处理的信号和经过自相关处理的信号分别输入到混沌振子系统中，得到的结果如表2所示。

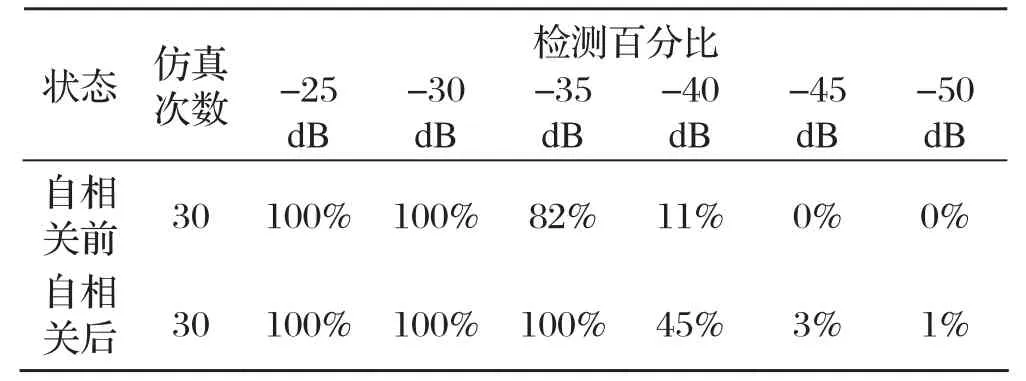
表2 自相关前后检测结果比较

由表2可以看出，基于自相关和混沌振子的检测方法，无论从仿真实验还是理论分析，都充分表明了这一方法对噪声是有很强的遏制能力且信噪比的门限较低。基于自相关和混沌振子的检测方法能够有效解决常规检测门限高这一现象，因此将该方法运用到实际工作中, 将拥有十分可观的发展前景。

5. 结论

（1）从数学模型和仿真究中证明了噪声对混沌振子检测微弱信号的影响，发现随意分布的零均值噪声很难使系统的原有轨迹发生变化。

（2）对于信噪比很低的微弱信号，采用自相关方法和混沌振子相结合，能够提高对噪声的抑制能力。

[1]张辉,王淑娟,张青森,等.基于小波包变换的滚动轴承故障诊断方法的研究[J].振动与冲击,2004,23(4):127-130.

[2]SUN Q,TANG Y.Singularity analysis using continuous wavelet transform for bearing fault diagnosis[J].Mechanical System and Signal Processing,2002,16(6):1025-1041.

[3]孙云岭,朴甲哲,张永祥.Wigner-Ville时频分布在内燃机故障诊断中的应用[J].中国机械工程,2004,15(6):505-507.

[4]杨宇,于德介.经验模态分解(EMD)在滚动轴承故障诊断中德应用[J].湖南大学学报(自然科学版),2003,30(5):25-28.

[5]焦卫东,朱有剑.基于EMD与倒谱分析的轴承故障诊断[J].机电工程,2009,26(2):18-21.

[6]王凤利,段树林,于洪亮,等.基于局域波和混沌的转子系统早期碰摩故障诊断[J].大连海事大学学报，2008,34(3):85-88.

[7]关贞珍,郑海起,杨云涛,等.基于经验模态分解和Duffing振子的轴承故障诊断术[J].农业机械学报,2010,41(9):214-217.

[8]刘秉正,彭建华.非线型动力学[M].北京:高等教育出版社, 2004:20-30.

[9]甘少波.微分方程动力系统与混沌导论[M].北京:人民邮电出版社,2008:40-50.

Research on Anti-noise Ability of Chaotic Oscillator to Detect Weak Signals

Liu Yan, Zhang Cui-xia, Zhang Ming-yu
（ Suzhou University, Suzhou Anhui 234002,China）

When using the chaotic oscillator in weak signal detection, as long as the containing known frequency of the signal to the frequency in the chaotic critical state of chaotic system, dynamical behavior of the chaotic system will have great changes.Often the input signal and noise are simultaneously acting on the chaotic system, which requires that the noise can not cause chaos system state changes.For this reason, the influence of noise on the chaotic oscillator system is analyzed by theoretical and numerical simulation.It propose a new method based on auto correlation method and chaotic system to detect weak signal.

weak signals; chaotic oscillator; random noises; auto correlation method

T H133；TP 274

A

1672-0547(2016)05-0110-03

2016-09-19

安徽省高校自然科学研究项目(KJ2016A776)；宿州学院煤矿机械与电子工程研究中心开放课题(2014YKF16)

刘 燕(1987-),女,安徽宿州人,宿州学院机械与电子工程学院教师,硕士,研究方向：设备故障诊断。