基于模糊方法的教学技能大赛二级模糊综合评价模型

成先娟,李克娥　(长江大学信息与数学学院，湖北 荆州 434023)



基于模糊方法的教学技能大赛二级模糊综合评价模型

成先娟,李克娥(长江大学信息与数学学院，湖北 荆州 434023)

[摘要]教学技能是教师在教育实践中练就的一种熟练的灵活多变的实际操作本领,是师范生未来职业生涯中最基本的职业技能和核心素质。在简要分析了模糊层次分析法和模糊综合评判2种系统评价方法特点的基础上，针对教学技能大赛评比指标的模糊性,利用科学的定量方法来刻画教学技能大赛评比中的定性问题，使定性分析与定量分析得到更好的融合，提出了师范生教学技能的二级模糊综合评判模型。该模型兼具2种方法的优点，能帮助决策者做出更为科学、合理、公正公平的决策，而且简便易行。

[关键词]模糊层次分析法；模糊综合评判；教学技能

教学技能是教师在教育实践中练就的一种熟练的灵活多变的实际操作本领,是师范生未来职业生涯中最基本的职业技能和核心素质[1]。目前，学者们在提高师范生的教学技能培养[2~5]方面和评价体标体系[6,7]进行了多方探索。然而教学技能考核是一个多层次、多目标的评价问题,评价涉及的内容较多，评价指标受考评者知识水平、认识能力和个人偏好的直接影响，很难完全排除人为因素带来的偏差。再则，评价指标一般都是定性描述，有鲜明的模糊特征，使得传统的评价法如直接打分法或是加权求和法不能够全面地反映出问题的本质，使得评价结果不能最大程度的反应客观事实。

目前，全国已举行了两届全国师范生教学技能竞赛，评委都是根据竞赛规则的规定给出量化分数，如教学设计下的一个子指标内容分析和学情分析都是满分2分，有的子准则满分甚至是1.5分，这就给评判专家出了一个难题：如何能给出公平、公正且让各位参评人员无异议的硬性分数呢？相对来说，若只要专家给出评语等级则容易多了。模糊数学[8]却能根据人类思维的特性， 给出更加合理的评价。为了让指标权重能更加真实的反应客观情况，摈弃专家个人主观偏见，笔者基于模糊层次分析法(FAHP)给出各级评价指标权重，结合模糊综合评判理论提出了一个基于FAHP的师范生教学技能的两级模糊综合评判模型，这既能克服因专家个人见解的偏差而产生的随意性，又可避免模糊数学方法中的模糊不确定性带来的误差，同时该方法又能对师范生进行分类，将对选用什么样的方法选拨优秀师范生提供理论依据。

1模糊层次分析法

层次分析法(The Analytic Hierarchy Process，AHP)是模糊数学和层次分析法相结合的产物，其理论和方法的应用已经比较成熟[7,9~15]。由于在构造两两比较的判断矩阵时所选取的标度系统与传统的层次分析法不同，使得如何由判断矩阵导出权重的方法以及一致性检验都与之有较大的差异。

FAHP在本质上是一种决策思维方式，运用FAHP进行决策时，大体可分为以下几个步骤：

1)分析决策系统中各因素之间的支配关系，按目标层和准则层建立评价对象的层次结构模型；

2)根据模糊标度0.1～0.9标度[14]构造模糊判断矩阵；

3)根据模糊判断矩阵导出指标权重；

4)作一致性检验。

2模糊综合评判原理

模糊综合评价是以模糊线性变换和最大隶属原则为其理论基础的综合决策方法[8]， 由于其在各个领域的成功应用，引起了越来越多的学者的广泛关注。但是，随着社会、经济的发展，所面临的问题受到越来越多的因素影响，使得专家很难对评判对象的指标权重做出合理的分配，对于这种多层模糊综合评判问题，笔者以两级模糊综合评判模型为例，其具体解题步骤如下：

第1步确定评价对象的因素集和评语集。评语集为V是确定师范生教学技能的分级，设有m个等级，V={v1,v2,…,vm}。根据因素的特性分成若干组U={U1,U2，…，Uk}，若Ui(i=1,2,…,k)满足：

(1)Ui≠Φ(i=1,2,…,k)；

(2)Ui∩Uj=Φ(i≠j)；

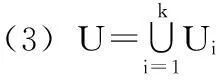
则称U={U1,U2,…,Uk}为第1级因素集，即有k个一级指标，Ui={ui1,ui2,…,uini} 为第2级因素集或因素子集，其中i=1,2,…,k,n1+n2+…+nk=n，这也说明有n个二级指标。

第2步由FAHP确定各级因素集的权重模糊集。针对第1步确定的因素集，记一级因素两两比较得到的模糊判断矩阵为P=(pij)k×k，并由权重计算公式[10]导出各个因素权重：

(1)

其中参数α越小，表明决策者越重视评价指标间的差异程度。不妨用A=(a1,a2,…,ak)表示一级指标的权重。类似计算二级因素集{ui1,ui2,…,umi}权重向量Ai=(ai1,ai2,…,ami)(i=1,2,…,k)。

第6步根据最大隶属原则，选择评价集B=(b1,b2,…,bm)中最大的bj对应的等级评语vj作为被评对象的综合评判的结果。

3教学技能的多级模糊评判模型

3.1师范生教学技能评价指标体系

表1　师范生教学技能的两级评判因子

作为职前教师，师范生教学技能的水平是衡量他们将来能否从事教师职业的重要标准，建立科学、客观、公正、可行的课堂教学质量评价体系和方法，是进行教学质量监控的有效保证。师范生教学技能是促进师范生教学技能成长，促进教师教育可持续发展的良好途径。文献[16]以华中师范大学师范教育实习生进行非结构化访谈，依据结合德尔菲法(专家咨询法)构建一套师范生教学技能评价体系；文献[17]基于调查统计法仅仅给出了数学教学技能的评价指标体系及权重，文献[6]着重就师范生教学技能的培养方法做了较为详述的探讨。但是，就各个专业的师范生教学技能的评价标准这一领域的研究成果不多，指标体系构造的好坏是评价成功与否的前提， 指标体系层次的多少应由考察问题的复杂性及评价所要达到的精度要求而定。笔者依据第2届全国师范院校师范生教学技能大赛依据的评判指标体系，建立了如表1所示的递阶层次结构，由5个一级指标与26个二级指标构成。使用基于模糊集理论的模糊层次分析法确定各级指标的权系数，可以使综合评价结果更公平、客观，具有更广泛的适用性。评语集是专家对被评价对象评价结果的直接描述。但是过于追求对研究对象的精确表达, 有时反倒使问题更加模糊深奥, 难以表达，适当的模糊化反而可以达到精确表达的目的。根据人的思维模糊特性和实际情况，对师范生的教学技能评价结果可分为5个等级，即V={v1,v2,…,v5} ={优，良，中，一般，差}。

3.2确定各级指标权重

选择合适的模糊标度并以此构造合理的模糊判断矩阵是利用模糊层次分析法求解实际问题的关键。模糊判断矩阵中的元素表示某2个影响因素相对于上一级评价指标的相对重要性程度之比的赋值，这些赋值的根据或来源可以依各个高校的实际情况而定，可以由教学主管部门决策者直接提供，也可由决策者和分析者共同确定， 或是由分析者通过各种技术咨询而获得。一般地，模糊判断矩阵应由熟悉师范生教学技能评价的专家独立地给出根据笔者建立的评价指标体系，专家根据评价因素和0.1～0.9标度[14](见表2)分别对各级指标作两两比较，建立两两比较的模糊判断矩阵。

表2　0.1～0.9模糊标度

设5个一级指标的两两比较的模糊糊判断矩阵为P=(pij)5×5,其中元素pij表示因素Ui与因素Uj具有模糊关系“Ui比Uj重要的隶属度”，由矩阵P和排序公式 (1)导出一级指标的权重A=(a1,a2,…,a5)，其具体表达式为：

对于表1中的各个一级指标下的二级指标，类似的求出如下所示的各个二级指标权重：

A1=(a11,a12,a17)A2=(a21,a22,…,a24)A3=(a31,a32,….a35)

A4=(a41,a42,…,a47)A5=(a51,a52,…,a53)

3.3构造模糊评判矩阵

3.4确定评价等级

根据层次总排序确定的教学技能比赛的评价指标权重A和一级模糊综合评判矩阵R，做如下的变换：

对B作归一化，得到:

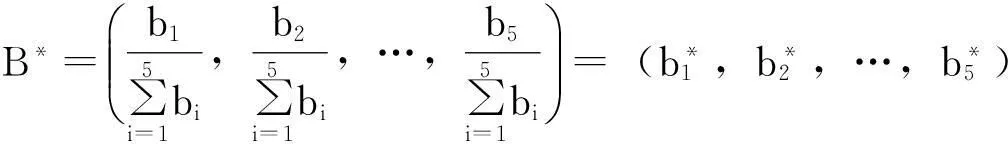
依最大隶属度原则， 取B*中的最大值作为评价等级。

4结论

1) 提出了应用模糊综合评价方法解决高校师范生的教学技能的评价问题，应用该方法有利于将各专家的定性分析定量化，通过科学的数学运算,作出合理的判断,有利于提高该问题的科学化水平。

2) 建立了高校师范生的教学技能的综合评价指标体系及模糊综合评价模型, 对师范生教学技能的培养这一领域的深入研究有相当的参考价值，但综合评价指标的设置针对不同的师范生培养对象可能不够全面或不尽合理, 有待于进一步的调整优化。

3)应用模糊综合评价法评价的科学性, 与模糊关系矩阵R及权重分配A有关。采用专家评判法确定R和A时,评判人员的组成及工作的独立性尤其重要，而这正是模糊层次分析法和模糊综合评价处理定性问题的优越性，能根据专家给出的判断矩阵给出客观的、合理的指标权重。

4) 评价方法可用于评价某一个方案的优劣,也可以对多个方案进行比较。

[参考文献]

[1]顾明远.教育大辞典[M].上海：上海出版社，1988:755.

[2]邹绍清. 免费师范生教学技能培养方式创新研究——基于师范生教学技能要素分析[J].西南大学学报(社会科学版)，2012,38(3):62～69.

[3]唐辉云.师范生教学技能支持系统的设计与实现[D].上海:上海师范大学，2008.

[4]李凌.运用微格教学培养体育师范生教学技能的设计与研究[J]. 西安体育学院学报,2007,24(4):118～120.

[5]朱广艳,李名,张豪锋.运用交互式电子白板培养师范生教学技能的实验研究[J].中国电化教育,2010(11):97～101.

[6]魏壮伟.师范生教学技能培养的方法体系构建[J].化学教育,2012(8)：54～56.

[7]方东辉,姜姗. 模糊层次分析法在师范技能评价体系中的应用[J]. 吉首大学学报(自然科学版),2012,33(6):107～110.

[8]陈水利,李敬功.模糊集理论及应用[M].北京:科学出版社,2005.

[9]成先娟. 不确定型层次分析法排序方法的研究[D].广西:广西大学,2006.

[10]吕跃进.基于模糊一致矩阵的层次分析法的排序[J].模糊数学与系统,2002,16(2):79~85.

[11]张吉军.模糊一致判断矩阵3种排序方法的比较研究[J].系统工程与电子技术，2003，25(11):1370～1372.

[12]吕跃进,程宏涛,覃菊莹.基于相对熵的互补判断矩阵排序方法[J]. 系统工程与电子技术，2011,31(7):1328～1333.

[13]成先娟，吕跃进.模糊判断矩阵排序的最小二乘法[A].2005年中国模糊逻辑与计算智能联合学术会议论文集[C].北京：海洋出版社,2005:152~157.

[14]杜栋.基于0.1～0.9标度的AHP再研究[J].系统工程与电子技术,2001,23(5): 36～38.

[15]姚敏，张森.模糊一致矩阵及其在软科学中的应用[J].系统工程，1997,15(2):54～57.

[16]卢丽静.高校师范生教学技能评价体系研究——基于华中师范大学教育实习生的调查[D].武汉：华中师范大学，2011.

[17]赵立强,李建红. 数学教学技能的分析与模糊评价[J]. 河北科技师范学院学报，2004,18(4):58～63.

[编辑]洪云飞

[引著格式]成先娟,李克娥.基于模糊方法的教学技能大赛二级模糊综合评价模型[J].长江大学学报(自科版)，2015,12(34)：1~4.

[中图分类号]O141

[文献标志码]A

[文章编号]1673-1409(2015)34-0001-04

[作者简介]成先娟(1981-)，女，硕士，讲师，现主要从事模糊数学、模糊决策等方面的研究工作；E-mail：chengxianjuan@126.com。

[基金项目]湖北省教育厅青年人才项目(20141306);长江大学基础学科科学研究发展基金(2013cjy03)。

[收稿日期]2015-08-19