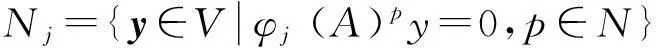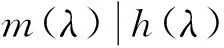矩阵有理标准形的性质研究及其应用

李绍刚

(1.桂林电子科技大学数学与计算科学学院;　2.广西密码学与信息安全重点实验室，广西桂林541004)



矩阵有理标准形的性质研究及其应用

李绍刚1，2

(1.桂林电子科技大学数学与计算科学学院;2.广西密码学与信息安全重点实验室，广西桂林541004)

[摘要]研究了矩阵的有理标准形理论，给出了友矩阵的主要性质和判断其相似对角化的条件，证明了线性定常系统的能控性，研究了伪随机数的生成过程和周期性，并对其在自动控制和计算机科学领域的应用做了一定的解读，最后用实例验证系统的有效性.

[关键词]友矩阵; 有理标准形; 状态方程； 能控系统； 伪随机数

1引言

矩阵的相似标准形理论应用非常广泛，复数域上任何一个矩阵均相似于一个若当标准形，任何数域上的矩阵则相似于一个有理标准形，可以证明一个复矩阵的有理标准形和其若当标准形是相似的，见文献[1]，由于没有数域上的限制，有理标准形在很多学科得到了广泛的应用，比如在微分方程组的计算[2]，群的构造[3]，对于有理标准形的Matlab软件计算，文献[4]给出了相应的算法，在计算机上可以轻松实现，以上均可以说明其应用是比较广泛的.

本文首先研究有理标准形的友矩阵的性质，其次研究了有理标准形在自动控制领域中状态方程的计算方面、计算机科学中的伪随机数生成器方面等的应用，最后进行了总结和归纳.

2基本理论

2.1　基本概念

定义1[5]对数域P上的一个多项式d(λ)=λn+a1λn-1+…+an称矩阵

(1)

为多项式d(λ)的伴侣阵，又称作友矩阵.

定义2[5]下列准对角矩阵

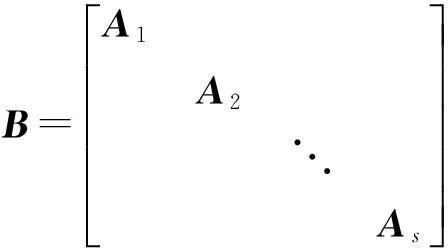
(2)

称为P上的一个有理标准形矩阵，其中Ai分别是数域P上某些多项式di(λ)(i=1,2,…,s)的伴侣阵，且满足d1(λ)|d2(λ)|…|ds(λ),d1(λ),d2(λ),…,ds(λ)的次数之和为n.

2.2　基本性质

友矩阵在有理标准形中起着至关重要的作用，其主要性质总结归纳如下：

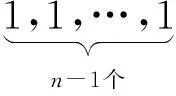
比如d(λ)=λ3+2λ2-3λ+1的伴侣阵为

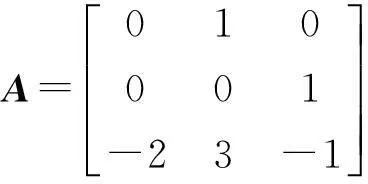
性质2有理标准形矩阵B的不变因子为1,1,…,1,d1(λ),d2(λ),…,ds(λ)，其中1的个数等于d1(λ),d2(λ),…,ds(λ)的次数之和n减去s.

性质3多项式d(λ)的友矩阵A的行列式det(A)=(-1)nan.利用性质3易知

性质4当an≠0，A可逆且

性质5多项式d(λ)的友矩阵A的特征多项式与最小多项式为

m(λ)=f(λ)=λn+a1λn-1+…+an.

性质1-5易证，证明从略.

2.3　基本定理

定理1[5]数域P上n×n方阵A在P上相似于唯一的一个有理标准形B，称为A的有理标准形.

有理标准形的具体计算步骤如下：

步骤1求出A的不变因子为d1(λ),d2(λ),…,dn(λ);

步骤2对每个次数大于0的不变因子di(λ)写出其对应的友矩阵Ai(i=1,2,…n);

利用以上3个步骤可以方便快捷的计算方阵的有理标准形，举例如下：

2.4　基本例题

例1设6阶矩阵A的不变因子为1,1,1,λ-1,(λ-1)(λ+2),(λ-1)2(λ+2)，求A的有理标准形.

解由不变因子可知三个伴侣阵为

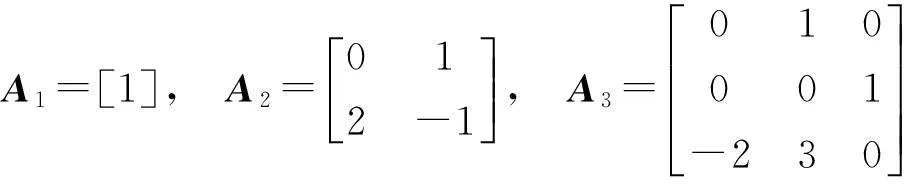
故可得A的有理标准形为

例2求矩阵

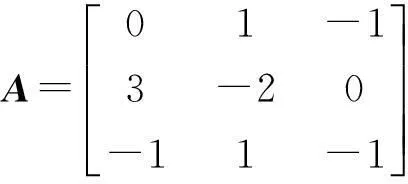
的有理标准形.

解A的不变因子为

d1(λ)=1,d2(λ)=1,d3(λ)=(λ-1)(λ2+4λ+2)=λ3+3λ2-2λ-2.

故A的有理标准形为

从以上两个例题不难发现，矩阵的有理标准形的计算依赖于矩阵不变因子的求解.

3重要应用

3.1　在自动控制领域中的应用

3.1.1基本概念与引理

定义3[6]以状态变量x1(t),x2(t),…,xn(t)构成的n维空间称为状态空间.

系统在任意时刻的状态向量x(t)在状态空间中是一个点，系统随时间的变化过程，使x(t)在状态空间中描绘出一条轨迹.

定义4[6]将反映系统动态过程的微分方程或传递函数，转换成一阶微分方程组的形式，并利用矩阵和向量的数学工具，将一阶微分方程组用一个式子来表示，这就是状态方程.

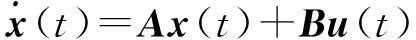
y(t)=Cx(t),

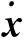
系统的能控性指的是控制作用对被控系统状态进行控制的可能性，对于给定的系统称其完全能控是指对任意初始时刻的任意一个初始状态总可以找到一个容许控制使系统在有限时间内达到目标状态.

引理1[6](代数判据)线性定常系统单输入系统

其状态完全能控的充条件是由A,b构成的能控性判别矩阵

Qc=(b,Ab,A2b…An-1b)

是行满秩矩阵，即有rank(Qc)=n.

引理2[6]线性定常系统经线性变换后状态能控性保持不变.

引理3[6](模态判据)线性定常系统单输入系统

其状态完全能控的充要条件是系统矩阵A的所有特征值λi(i=1,2…n)满足

rank(λiE-A,b)=n,i=1,2…n.

代数判据的优点是方便计算，缺点是无法确定状态空间中哪些变量(特征值、极点)能控；模态判据的优点是易于确定哪些变量能控，缺点是需要求系统的特征值.这两类方法优势互补，可根据实际情况选择合适的方法.

3.1.2状态方程的建立

下面以控制系统状态方程为例给出线性定常连续与离散系统状态空间方程的构造过程.

为方便起见，记号如下：

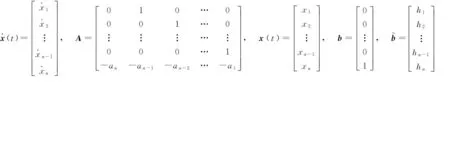
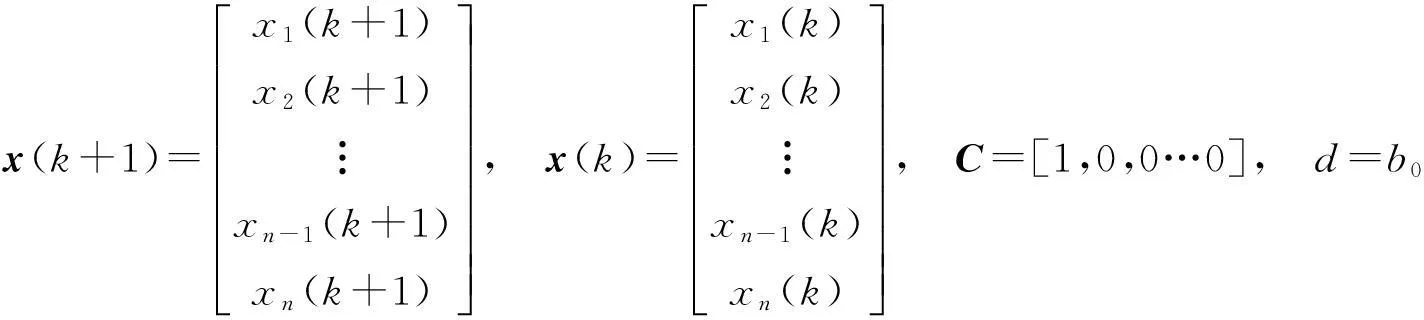
情形1线性定常连续系统状态方程

(i)

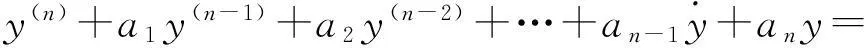
选取y和y(i)为系统状态向量，记

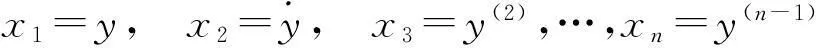
则上述方程可化为n个一阶常微分方程

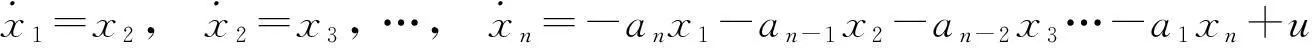
写成矩阵形式为

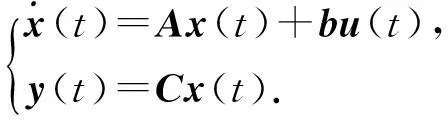
(ii) 作用函数含导数项

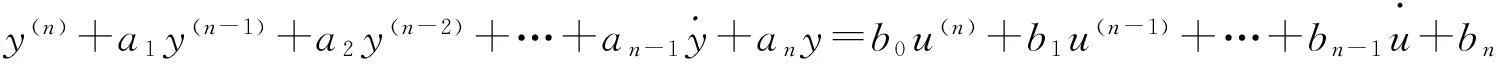
选取y和y(i)为系统状态向量，记

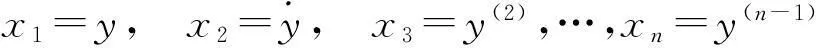
则上述方程可化为n个一阶常微分方程

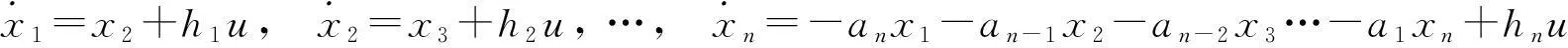
其中

h1=b1-a1b0,h2=(b2-a2b0)-a1h1…hn=(bn-anb0)-an-1h1-…-a1hn-1.

矩阵形式为

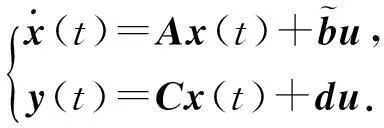
情形2线性定常离散系统状态方程

(i)作用函数不含未来项

y(k+n)+a1y(k+n-1)+…+an-1y(k+1)+any(k)=u(k).

选取状态变量为

x1(k)=y(k),x2(k)=y(k+1),…，xn(k)=y(k+n-1),

根据离散系统差分方程可得状态方程

x1(k+1)=x2(k),

x2(k+1)=x3(k+1),

……

xn(k+1)=-anx1(k)-an-1x2(k)-…-a2xn-1(k)-a1xn(k)+u(k).

矩阵形式为

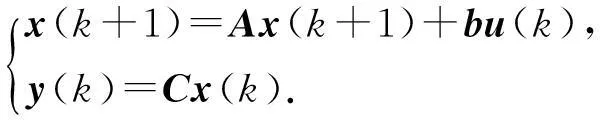
(ii)作用函数含未来项

y(k+n)+a1y(k+n-1)+…+an-1y(k+1)+any(k)

=b0u(k+n)+b1u(k+n-1)+…+bn-1u(k+1)+bnu(k).

选取状态变量为

x1(k)=y(k)-b0u(k),

x2(k)=x1(k+1)-h1u(k),

……

xn(k)=xn-1(k+1)-hn-1u(k),

其中

h1=b1-a1b0,

h2=(b2-a2b0)-a1h1,

……

hn=(bn-anb0)-an-1h1-…-a1hn-1.

根据离散系统差分方程可得状态方程

x1(k+1)=x2(k)+h1u(k),

x2(k+1)=x3(k)+h2u(k),

……

xn(k+1)=-anx1(k)-an-1x2(k)-…-a2xn-1(k)-a1xn(k)+hnu(k).

矩阵形式为

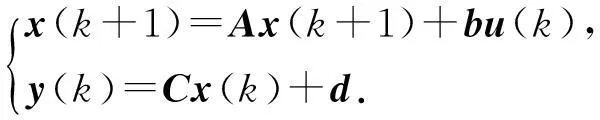
经过适当的选取状态变量，上述系统均可以转化为带有友矩阵的状态方程.

3.1.3主要结论

上述所有系统中的矩阵均为伴侣阵(友矩阵)，为方便系统的研究，对友矩阵进行相似对角化显得尤为必要，下面给出友矩阵相似对角化的条件，即有如下结论.

定理2设A为d(λ)=λn+a1λn-1+…+an的伴侣阵，若d(λ)=0有n个不同的根λ1,λ2,…，λn，则存在可逆矩阵P使得P-1AP=Λ，其中Λ=diag{λ1,λ2,…,λn}，

证利用性质5可知

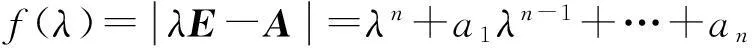
只需验证AP=PΛ.注意到λ1,λ2,…λn也为A的n个特征值，且

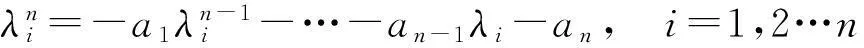
从而有

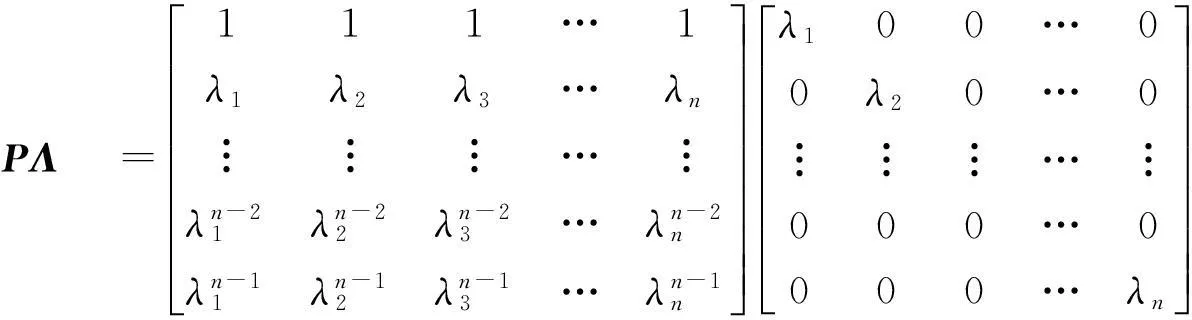
比较以上两式即证AP=PΛ.

定理3线性定常系统单输入系统

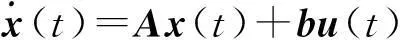
其状态是完全能控的, 称为能控标准形.

证Qc=(b,Ab,A2b,…,An-1b)

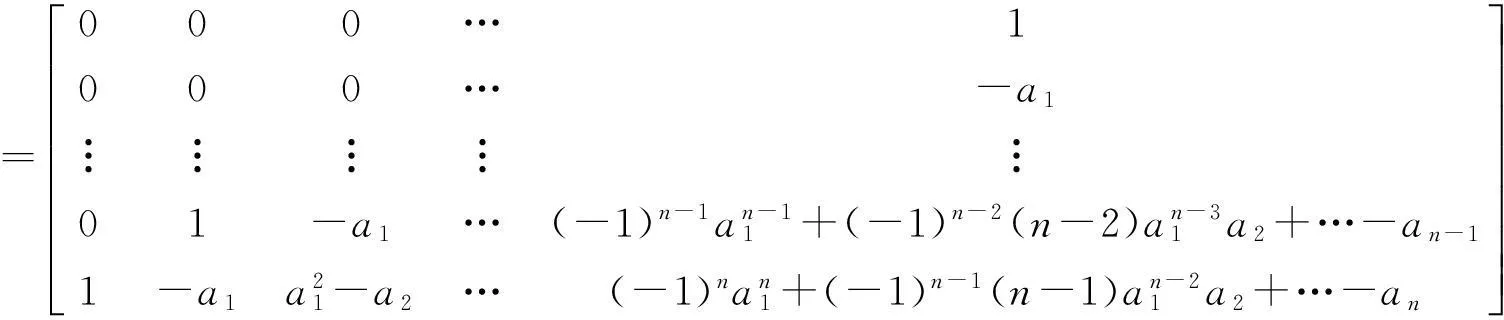
为斜对角线上元素均为1的下三角形矩阵，从而rank(Qc)=n，即能控矩阵为行满秩矩阵，由引理1可知上述系统为完全能控的.

例3将状态方程

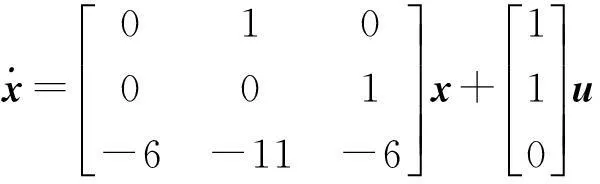
化为对角标准形，并判别系统的能控性.

解特征方程为

f(λ)=λ3+6λ2+11λ+6=(λ+1)(λ+2)(λ+3)=0,

特征值为λ1=-1,λ2=-2,λ3=-3，系统矩阵为友矩阵，且特征值互异，故可以对角化，其变换矩阵

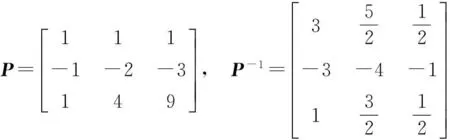
故线性变换后的状态空间表达式为

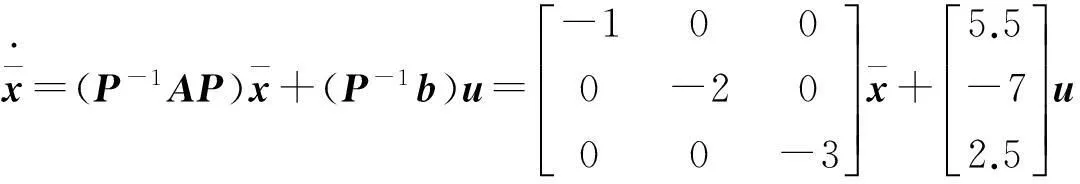
由引理2可知线性变换不改变系统的能控性，又注意到

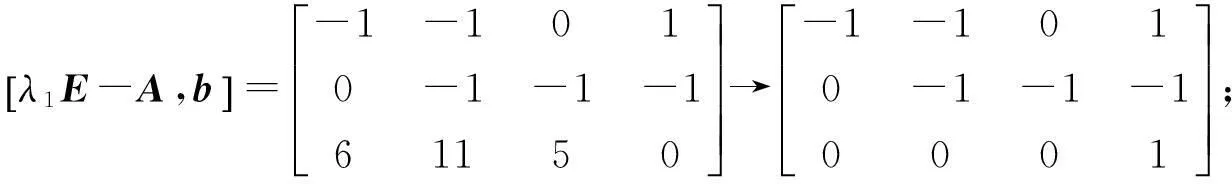
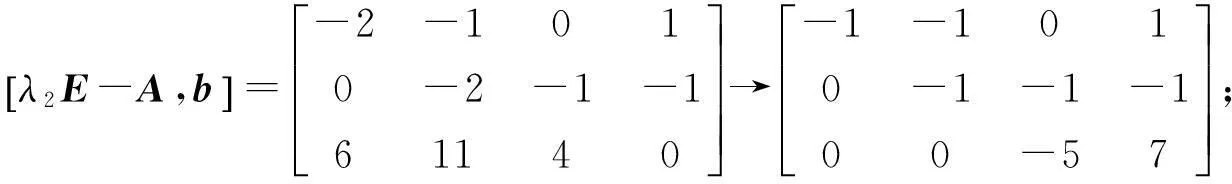
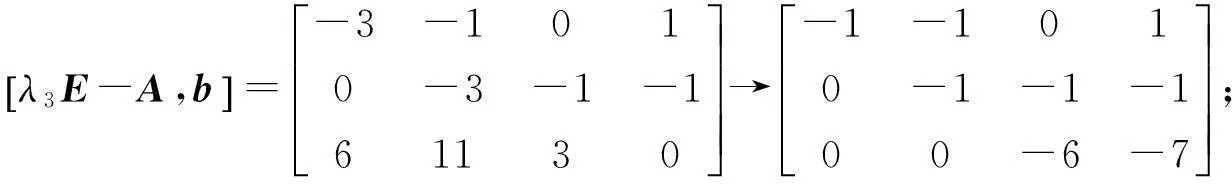
故有rank(λiE-A)=3=n(i=1,2,3),从而系统可控.

例4已知某离散系统的差分方程为

y(k+3)+3y(k+2)+y(k+1)+2y(k)=u(k),

试求其状态空间表达式.

解选状态变量

x1(k)=y(k)，x2(k)=y(k+1)，x3(k)=y(k+2)，

则直接写出状态空间表达式如下

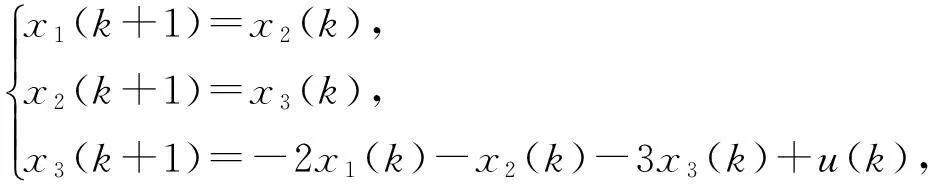
y(k)=x1(k),

写成矩阵形式

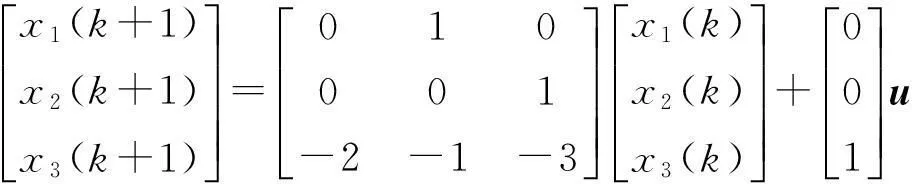
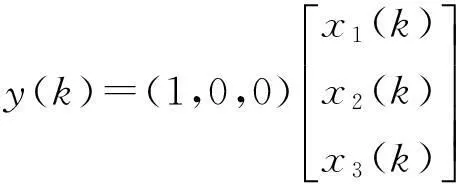
由引理3可知该系统为能控标准形，若改变选择状态变量的方法，也可以将该离散系统的差分方程转换成另一种形式的状态空间表达式.

3.2　在伪随机数中的应用

真正意义上的随机数是在某次产生过程中按照实验过程中表现的分布概率随机产生的，其结果是不可预测的，是不可见的.而计算机中的随机函数是按照一定算法模拟产生的，其结果是确定的，是可见的.这个可预见的结果其出现的概率是必然的.所以用计算机随机函数所产生的“随机数”并不随机，是伪随机数.

伪随机数中一个很重要的概念就是“种子”，种子决定了伪随机数的固定序列，下面构造迭代序列xn+1=Axn, 其中A为上述定义的友矩阵，A的元素ai∈Z2,i=1,2,…n,Z2表示只包含0与1的集合，上述序列可以看成“种子”，利用循环子空间的概念和线性空间的直和分解，可以得到伪随机数生成的重要结果.

定义5[7]设σ是n维线性空间V上的线性变换，若存在α∈V使得向量组

α,σ(α),σ2(α)…σn-1(α)

线性无关，且σn(α)可由该向量组性表示，则称向量组为V的循环基，称张成的子空间

L(α,σ(α),σ2(α)…σn-1(α))

为V上的循环子空间，σ称为循环变换.

引理4[7]设V是复数域上的线性空间，对于V上的任意幂零变换σ，V必可分解为循环子空间的直和

V=T1⊕T2⊕…⊕Tt

使得σ限制在每个循环子空间Ti为循环变换.

Apy=y,Ary≠y，1

其中y∈V.

证若A可逆，则A是线性空间V的一个排列，则y∈V,y的周期不超过2n.设A的最小多项式为

m(λ)=φ1(λ)n1φ2(λ)n2…φk(λ)nk，

V=N1⊕N2⊕…⊕Nk,

每个Nj的循环基向量合并在一起就可以构成V的一组基，不妨假设Nj的循环基为

vj,1,Avj,1,…,Asj,1vj,1,

vj,2,Avj,2,…,Asj,2vj,2,

…

vj,sj,Avj,sj,…,Asj,sjvj,sj.

h(A)=Ap-1=0,(Ap-1)y=0.

即证Apy=y,y∈V.

对于友矩阵A，其最小多项式为

m(λ)=λn+a1λn-1+…+an.

容易求出，进而可得伪随机数的生成过程.

4结论

本文研究了矩阵的有理标准形中的伴侣矩阵的性质，对有理标准形在自动控制领域和计算机中伪随机数的产生等进行了较为深入的探讨，作为矩阵的一类等价标准类，相比其他标准类不受数域的影响.

[参考文献]

[1]王莲花. 矩阵的若尔当标准形与有理标准形的关系探究[J].河南教育学院学报，2009，18(3)：3-4.

[2]呙林兵. 矩阵的有理标准形的一些应用[J]. 怀化学院学报， 2009，28(5)：38-39.

[3]杨晓萍, 海进科. 矩阵的有理标准形在群构造中的一些应用[J]. 青岛大学学报，2007，20(4)：13-17.

[4]张丹丹. 矩阵的有理标准型的求法在Matlab中的实现[J]. 湖北工业大学学报，2011，26(5)：107-109.

[5]北京大学数学系几何与代数教研室.高等代数 [M].3版. 北京：高等教育出版社，2003.

[6]孙优贤,王慧. 自控控制原理[M]. 北京：化学工业出版社，2011.

[7]张贤科，许甫华. 高等代数学 [M]. 2版. 北京：清华大学出版社，2008.

The Study on the Property of Matrix Rational

Canonical Forms and its Application

LIShao-gang1,2

(1.School of Mathematics and Computational Science, Guangxi Key Laboratory of Cryptography and Information Security,

2.Guilin University of Electronic Technology, Guilin, Guangxi 541004,China)

Abstract:This paper studies the theory of rational canonical forms about matrix, some properties of companion matrix and conditions of diagonalization are given，the controllability of linear time-invariant system are proved, the formation process and periodicity about pseudo-random numbers also studied. Furthermore, application of rational canonical forms in automatic control and computer science are stated in some interpretation. At last, the reliability of systems are validated by actual examples.

Key words:companion matrix; rational canonical forms; equation of state; control system; pseudo-random number

[基金项目]广西区精品课程线性代数项目；线性代数课程与工程应用型人才培养相结合的混合教学模式研究项目

[收稿日期]2014-12-20；[修改日期]2015-03-28

[中图分类号]O151.21

[文献标识码]C

[文章编号]1672-1454(2015)02-0076-08