高温高压CO2状态方程研究

韩 勇, 郭向利, 龙新平

(1. 中国工程物理研究院化工材料研究所, 四川 绵阳 621999; 2. 中国工程物理研究院, 四川 绵阳 621999)

1 引 言

炸药爆轰时,爆轰产物处于高温高压状态,爆轰产物压力由数十吉帕逐渐衰减至兆帕量级,温度也由数千开尔文逐渐衰减至1000K甚至更低,建立能够准确描述爆轰产物气体高温、高压的状态方程对有效表征爆轰产物状态变化过程具有十分重要的意义。

目前,实现爆轰产物气体所处的高温、高压试验条件十分困难,关于高温、高压气体状态的实验数据很少。分子动力学(MD)/蒙特卡洛方法(MC)是研究爆轰产物气体高温高压热力学性质的有力工具,它们通过有限的分子数目,结合边界的约束处理,能够准确计算气体的宏观热力学性质。然而MD方法和MC方法计算耗时,且无法直接应用。解析形式的状态方程则可以直接应用于实际问题,形成子程序直接纳入相关程序中应用。在描述爆轰产物气体方面,已有BKW[1]、VLW[2]、LJD[3]、JCZ[4]等解析状态方程形式。其中,VLW状态方程为我国吴雄教授借鉴相似理论,认为各阶维里系数在高温下是相似的,高阶维里系数可以通过二阶维里系数求得,进而将维里物态方程以一种简化形式写出,形成了VLW爆轰产物状态方程[5-6],其成功应用于炸药爆轰性能的理论计算。与BKW状态方程相比,VLW状态方程在描述爆轰环境下气体高温高压热力学状态时有了一定改善。然而VLW状态方程形式仍然存在一些不足,VLW状态方程不能有效描述爆轰产物气体组分的高温高压热力学状态,从而使其所采用的爆轰产物势参数缺乏必要的物理基础支撑。作者[7]前期应用VLW状态方程计算H2O冲击Hugoniot曲线的结果表明,即使在优化后的势参数条件下,VLW状态方程仍然不能在宽的压力范围有效描述H2O的高温高压状态。

针对VLW状态方程存在的上述不足,本研究提出了一种描述爆轰环境下高温、高压气体的对比态维里型状态方程VHL(Viral-Han-Long),该状态方程基于LJ势能函数,通过对炸药爆轰产物中的重要气体组分CO2高温高压热力学状态的描述,表明对比态VHL状态方程能够有效地描述爆轰环境下CO2气体的压力、体积和温度(pVT)热力学关系。

2 对比态VHL状态方程

理论上,任何气体的状态方程,都可以用维里形式描述。然而,实践中随着维里系数阶数的提高,计算的复杂性迅速增大。Barker等[8]基于LJ势能函数,针对无量纲第三阶、第四阶、第五阶系数,进行了精确的理论计算,其以表格形式列出了特定温度时的系数值,不适宜实际使用。在前期研究中,作者等[9]提出用一种简化维里型状态方程形式描述高温甲烷气体的热力学pVT状态。为有效描述爆轰环境下其它气体产物的pVT热力学关系,本研究提出了一种基于对比态原理的维里型状态方程形式VHL,表达式见(1)。

(1)

C*=c1T*c2+c3T*c4+c5T*c6+c7T*c8+c9T*c10

D*=d1T*d2+d3T*d4+d5T*d6+d7T*d8+d9T*d10

E*=e1T*e2+e3T*e4

b0=2πNσ3/3

式中,p为气体实际压力,GPa;V为摩尔体积,cm3·mol-1;T为温度,K;R为摩尔气体常数8.3145,J·mol-1·K-1;N为阿佛加德罗常数6.022045×1023mol-1,第二阶无量纲维里系数B*采用变步长辛卜生求积法近似计算获得[10];C*、D*分别为第三阶和第四阶无量纲维里系数,c1～c10、d1～d10为常数,通过该表达式所得第三阶和第四阶无量纲维里系数值与理论值十分吻合; 对于第五阶以上的无量纲维里系数,则采用组合函数表示,其系数值e1～e4、a、b、f由无极性分子CH4的热力学数据[11-12](温度1000 K以上的112组pVT数据)确定; 各阶维里系数的拟合常数获得方式见文献[9]所述,具体数值见表1。T*为无量纲温度,bCH4为67.21,w为对比态参量,VHL状态方程通过参量w实现其它气体与甲烷状态方程的对比。ε、σ为LJ势参数。

表1VHL状态方程中各阶维里系数拟合常数值

Table1Fitting constant values of each order viral coefficient in VHL Equation of State(EOS)

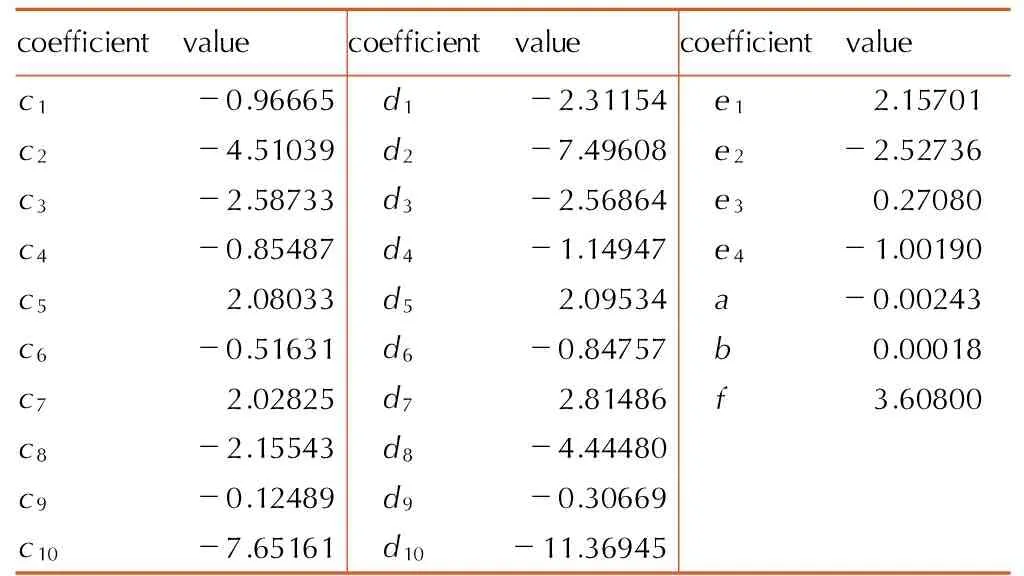
coefficientvaluecoefficientvaluecoefficientvaluec1-0.96665 d1-2.31154 e12.15701c2-4.51039 d2-7.49608 e2-2.52736c3-2.58733 d3-2.56864 e30.27080c4-0.85487 d4-1.14947 e4-1.00190c52.08033 d52.09534 a-0.00243c6-0.51631 d6-0.84757 b0.00018c72.02825 d72.81486 f3.60800c8-2.15543 d8-4.44480c9-0.12489 d9-0.30669c10-7.65161 d10-11.36945

3 CO2气体高温高压热力学状态的计算

由于液态CO2样品制备条件苛刻、难度大,其高温、高压的基础实验数据较少。1990年初,Schott等[13]才发表了用化爆技术在5～30 GPa区域获得的一组试验点。Nellis等[14]用二级轻气炮技术在25～70 GPa区域获得了一组试验点。刘福生等[15]利用二级轻气炮作冲击加载手段,获得了CO2在20～60 GPa区域六个Hugoniot数据点。实验数据点偏少,且缺乏温度的直接测量数据。因此,本研究以Belonoshko等[12]的分子动力学计算数据作为CO2的基础数据,温度范围为718～4978 K,压力范围为0.5116～111.078 GPa,基于VHL状态方程,应用复形调优法[16]优化了CO2的LJ势参数,势参数值与文献值比较见表2所示。采用VHL、VLW状态方程计算结果和分子动力学计算值比较见表3所示,不同温度或压力下CO2体积计算偏差如图1、图2所示。由表3、图1和图2可得,采用VHL状态方程计算得CO2体积平均绝对偏差为0.971%,最大偏差为4.04%, VHL状态方程计算所得体积偏差与压力和温度参量无明显的相关性。VLW状态方程计算所得体积偏差则与温度具有明显的相关性,在较低温度下,计算所得体积偏差较大，最大偏差87.149%,随着温度的升高,计算体积偏差逐渐减小,但仍普遍高于VHL状态方程计算结果,采用VLW状态方程计算所得平均绝对偏差20.2%。

表2本研究所采用CO2势参数值与文献值比较

Table2Comparison of the potential parameter values of CO2used in this paper and literature ones

(ε/k)/Kb0/mL·mol-1reference247.063.37[17]205.085.05[5]181.867.30thispaper

图1不同压力下VHL状态方程、VLW状态方程预测CO2的体积误差百分比

Fig.1Error percentage of volume predicted by VHL EOS and VLW EOS at different pressure

图2不同温度下VHL状态方程、VLW状态方程预测CO2的体积误差百分比

Fig.2Error percentage of volume predicted by VHL EOS and VLW EOS at different temperature

为验证对比态VHL状态方程在更低压力下的有效性,同时与VLW状态方程计算结果比较,本研究引

用NIST数据库的数据[18],对CO2在1000 K,20～800 MPa的热力学状态进行了计算,结果见表4所示。采用对比态VHL状态方程计算得CO2体积绝对平均偏差为0.698%,采用VLW状态方程计算所得体积绝对平均偏差为11.988%。在固定温度1000 K条件下,随着压力的增加,VLW计算所得体积偏差逐渐增大,在压力为800 MPa时,体积偏差最大达-19.771%。其原因可能与VLW状态方程形式的高阶维里系数过度简化有关,随着压力增大,描述多个气体分子同时相互作用的高阶维里系数的准确性要求提高,而VLW状态方程中,除第二阶维里系数与理论值相符合外,随着维里系数阶级的增大,其与理论值的差距也逐渐增大,故CO2的体积计算结果偏差随压力增大而增大。而本文所提出的对比态VHL状态方程的第三阶、第四阶维里系数均与理论值吻合,高阶维里系数则通过甲烷高温高压热力学状态数据优化获得,其具有扎实物理基础,因此,该状态方程能够很好描述CO2高温状态下较低压力范围内的热力学状态。

表3VHL、VLW状态方程计算CO2高温pVT关系

Table3ThepVTrelation of CO2at high temperature calculated by the means of VHL EOS and VLW EOS

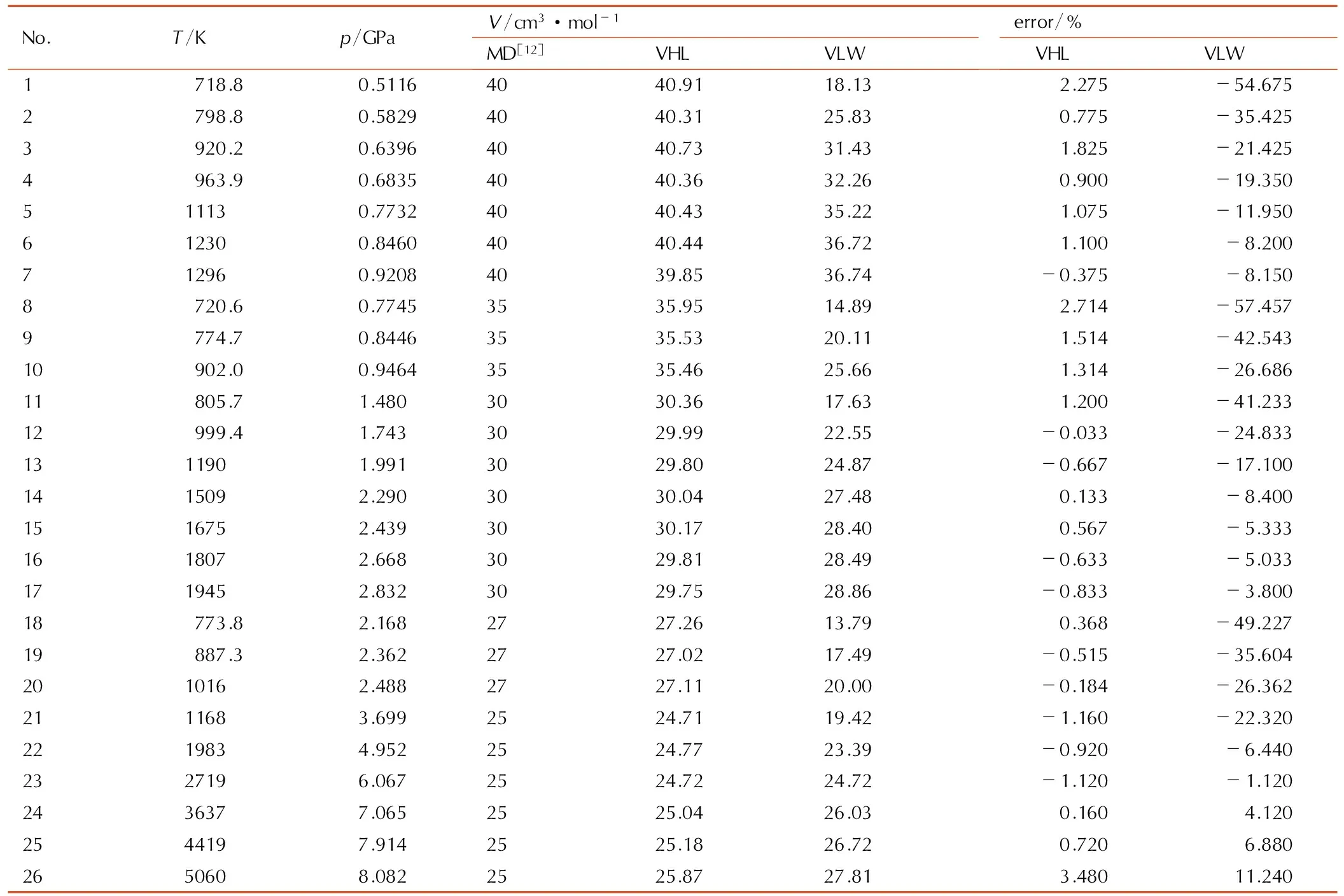
No. T/K p/GPaV/cm3·mol-1MD[12]VHLVLWerror/% VHL VLW1718.80.51164040.9118.132.275-54.6752798.80.58294040.3125.830.775-35.4253920.20.63964040.7331.431.825-21.4254963.90.68354040.3632.260.900-19.350511130.77324040.4335.221.075-11.950612300.84604040.4436.721.100-8.200712960.92084039.8536.74-0.375-8.1508720.60.77453535.9514.892.714-57.4579774.70.84463535.5320.111.514-42.54310902.00.94643535.4625.661.314-26.68611805.71.4803030.3617.631.200-41.23312999.41.7433029.9922.55-0.033-24.8331311901.9913029.8024.87-0.667-17.1001415092.2903030.0427.480.133-8.4001516752.4393030.1728.400.567-5.3331618072.6683029.8128.49-0.633-5.0331719452.8323029.7528.86-0.833-3.80018773.82.1682727.2613.790.368-49.22719887.32.3622727.0217.49-0.515-35.6042010162.4882727.1120.00-0.184-26.3622111683.6992524.7119.42-1.160-22.3202219834.9522524.7723.39-0.920-6.4402327196.0672524.7224.72-1.120-1.1202436377.0652525.0426.030.1604.1202544197.9142525.1826.720.7206.8802650608.0822525.8727.813.48011.240

Table3continued

No. T/K p/GPaV/cm3·mol-1MD[12]VHLVLWerror/% VHL VLW27700.84.4822222.662.7994.040-87.14928812.94.7212222.4511.923.076-45.27129913.44.9552222.3114.032.433-35.5833010245.2902222.1215.431.561-29.1553112187.9302020.1915.350.950-23.25032186410.522019.5617.35-2.200-13.25033262812.182019.6318.86-1.850-5.70034432115.052019.9220.70-0.4003.50035497816.362019.8821.00-0.6005.00036803.211.351818.238.881.278-50.68937122812.471818.0013.310.000-26.05638164113.561818.0015.070.000-16.27839197714.521817.9915.94-0.056-11.44440241415.641818.0216.770.111-6.83341275616.741817.9617.17-0.222-4.61142316117.561818.0417.680.222-1.77843346918.241818.0617.990.333-0.05644783.019.471616.147.190.875-55.08745118620.621615.8811.14-0.750-30.37546164521.921615.8812.91-0.750-19.31347200622.941615.9213.79-0.500-13.81348231824.111615.9014.31-0.625-10.56249277025.071616.0015.010.000-6.18750307226.321615.9415.27-0.375-4.56351338427.041615.9915.59-0.063-2.56252395627.991616.1216.160.7501.00053803.726.221515.097.010.600-53.28054119527.391514.8510.27-1.000-31.53355160828.631514.8311.77-1.133-21.53356206929.971514.8712.81-0.867-14.60057240030.921514.9113.36-0.600-10.93358271131.951514.9213.77-0.533-8.20059307532.891514.9714.19-0.200-5.40060340133.671515.0114.520.067-3.20061393834.741515.1015.010.6670.06762787.235.671414.126.170.857-55.90063121937.021413.849.51-1.143-32.07164165938.361413.8110.91-1.357-22.07165205039.581413.8311.71-1.214-16.35766234040.501413.8512.17-1.071-13.07167279341.971413.8912.74-0.786-9.00068319042.681413.9613.19-0.286-5.78669340144.181413.9013.29-0.714-5.07170789.649.451313.145.701.077-56.12371119250.771312.868.57-1.077-34.05472159452.071312.819.80-1.462-24.64673198453.321312.8210.57-1.385-18.69274231354.381312.8411.07-1.231-14.84675288656.211312.8711.74-1.000-9.69276307957.431312.8511.89-1.154-8.53877355158.001312.9312.34-0.538-5.07778395658.711312.9912.67-0.077-2.53879782.069.771212.215.111.750-57.425

Table3continued

No. T/K p/GPaV/cm3·mol-1MD[12]VHLVLWerror/% VHL VLW80120871.241211.917.86-0.750-34.52581161372.641211.848.94-1.333-25.50882199173.981211.839.61-1.417-19.91783240775.371211.8410.17-1.333-15.25084285476.901211.8610.64-1.167-11.33385323878.241211.8710.97-1.083-8.58386349879.161211.8811.16-1.000-7.00087807.0100.71111.264.962.364-54.882881209102.21110.987.12-0.182-35.264891599103.61110.908.06-0.909-26.755901971104.91110.888.66-1.091-21.273912416106.61110.879.20-1.182-16.400922866108.11110.889.63-1.091-12.500933012109.21110.879.73-1.182-11.545943326109.61110.899.98-1.000-9.236953959111.11110.9210.41-0.727-5.364

Note: error=100×(VEOS-VMD)/VMD

表41000 K时CO2pVT关系的VHL、VLW状态方程计算值及与NIST数据库数据的比较

Table4Comparison of the calculated values of CO2pVTrelation at 1000 K by VHL EOS and VLW EOS and the data of CO2in NIST database

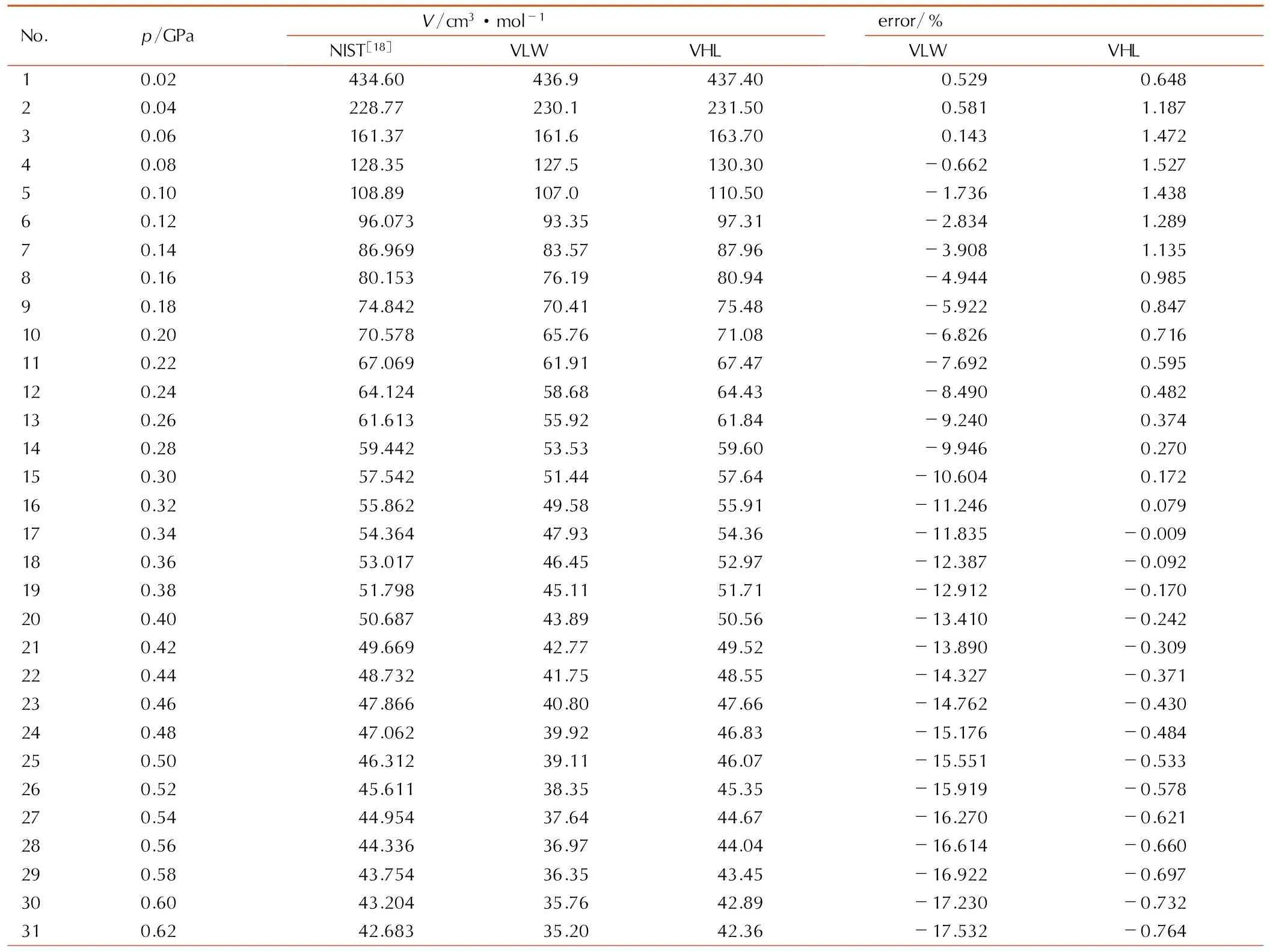
No.p/GPa V/cm3·mol-1 NIST[18] VLW VHLerror/% VLW VHL10.02434.60436.9437.400.5290.64820.04228.77230.1231.500.5811.18730.06161.37161.6163.700.1431.47240.08128.35127.5130.30-0.6621.52750.10108.89107.0110.50-1.7361.43860.1296.07393.3597.31-2.8341.28970.1486.96983.5787.96-3.9081.13580.1680.15376.1980.94-4.9440.98590.1874.84270.4175.48-5.9220.847100.2070.57865.7671.08-6.8260.716110.2267.06961.9167.47-7.6920.595120.2464.12458.6864.43-8.4900.482130.2661.61355.9261.84-9.2400.374140.2859.44253.5359.60-9.9460.270150.3057.54251.4457.64-10.6040.172160.3255.86249.5855.91-11.2460.079170.3454.36447.9354.36-11.835-0.009180.3653.01746.4552.97-12.387-0.092190.3851.79845.1151.71-12.912-0.170200.4050.68743.8950.56-13.410-0.242210.4249.66942.7749.52-13.890-0.309220.4448.73241.7548.55-14.327-0.371230.4647.86640.8047.66-14.762-0.430240.4847.06239.9246.83-15.176-0.484250.5046.31239.1146.07-15.551-0.533260.5245.61138.3545.35-15.919-0.578270.5444.95437.6444.67-16.270-0.621280.5644.33636.9744.04-16.614-0.660290.5843.75436.3543.45-16.922-0.697300.6043.20435.7642.89-17.230-0.732310.6242.68335.2042.36-17.532-0.764

Table4Continued

No.p/GPaV/cm3·mol-1NIST[18]VLWVHLerror/%VLWVHL320.6442.18934.6741.85-17.822-0.794330.6641.71934.1741.38-18.095-0.822340.6841.27233.7040.92-18.347-0.848350.7040.84533.2440.49-18.619-0.872360.7240.43832.8140.08-18.863-0.896370.7440.04932.4039.68-19.099-0.920380.7639.67632.0139.30-19.322-0.941390.7839.31931.6338.94-19.555-0.963400.8038.97631.2738.59-19.771-0.983

Note: error=100×(VEOS-VNIST)/VNIST.

4 结 论

本研究提出了一种基于LJ势能函数的对比态维里型状态方程VHL用于描述爆轰环境下CO2的高温高压热力学状态。采用VHL状态方程计算得CO2体积平均绝对偏差为0.971%,最大偏差为4.04%,采用VLW状态方程计算所得平均绝对偏差20.2%,最大偏差87.149%。因此,在计算CO2高温、中高压热力学状态时,VHL状态方程的计算准确性得到了大幅度提高。VHL状态方程计算所得体积偏差与压力和温度参量无明显的相关性; VLW状态方程计算所得体积偏差则与温度具有明显的相关性,随着温度的升高,计算体积偏差逐渐减小。

参考文献:

[1] Mader C L. Numerical modeling of explosives and propellants[M]. CRC press, 2007: 377-380.

[2] 吴雄, 龙新平, 何碧, 等. VLW 爆轰产物状态方程[J]. 中国科学: B 辑, 2008, 38(12): 1129-1132.

WU Xiong,LONG Xin-ping, HE Bi, et al. VLW equation of state of detonation products[J].ScienceinChinaSeriesB:Chemistry, 2008, 38(12): 1129-1132.

[3] Fickett W, Wood W W. Tables of the Lennard-Jones and Devonshire equation of state at high temperatures and densities[J].TheJournalofChemicalPhysics, 1952, 20(10): 1624-1626.

[4] Fried L E, Howard W M. An accurate equation of state for the exponential-6 fluid applied to dense supercritical nitrogen[J].TheJournalofChemicalPhysics, 1998, 109(17): 7338-7348.

[5] 吴雄, 龙新平, 何碧, 等. VLW状态方程的回顾与展望[J]. 高压物理学报, 1999, 13(1): 55-58.

WU Xiong, LONG Xin-ping, HE Bi, et al. Review and look forward to the progress of VLW equation of state[J].ChineseJournalofHighPressurePhysics, 1999, 13(1): 55-58.

[6] 龙新平, 何碧, 蒋晓华, 等. 论VLW状态方程[J]. 高压物理学报, 2003, 17(4): 247-254.

LONG Xin-ping, HE Bi, JIANG Xiao-hua, et al. Discussions on the VLW equation of state[J].ChineseJournalofHighPressurePhysics, 2003, 17(4): 247-254.

[7] 韩勇, 龙新平, 蒋治海, 等. 用VLW状态方程计算水的冲击Hugoniot曲线[J]. 爆炸与冲击, 2010, 30(1): 17-20.

HAN Yong, LONG Xin-ping, JIANG Zhi-hai, et al. A theoretical calculation for the hugoniot of water using the VLW equation of state[J].ExplosionandShockWaves, 2010, 30(1): 17-20.

[8] Barker J A, Leonard P J, Pompe A. Fifth virial coefficients[J].TheJournalofChemicalPhysics, 1966, 44(11): 4206-4211.

[9] 韩勇, 龙新平, 郭向利. 一种简化维里型状态方程预测高温甲烷pVT关系[J]. 物理学报, 2014, 63(15): 150505.

HAN Yong, LONG Xin-ping, GUO Xiang-li. Prediction of methane pVT relations at high temperatures by a simplified virial equation of state[J].ActaPhysSin, 2014, 63(15): 150505.

[10] 韩勇, 龙新平, 黄毅民, 等. L-J, Exp-6 两种形式势能函数对计算无量纲第二维里系数的影响[J]. 含能材料, 2009, 17(5): 574-577.

HAN Yong, LONG Xin-ping, HUANG Yi-min, et al. Effect of L-J or Exp-6 potential function on calculation of reduced second Viral coefficient[J].ChineseJournalofEnergeticMaterials(HannengCailliao), 2009, 17(5): 574-577.

[11] Duan Z, Møller N, Weare J H. Molecular dynamics simulation of PVT properties of geological fluids and a general equation of state of nonpolar and weakly polar gases up to 2000 K and 20,000 bar[J].GeochimicaetCosmochimicaActa, 1992, 56(10): 3839-3845.

[12] Belonoshko A, Saxena S K. A molecular dynamics study of the pressure-volume-temperature properties of supercritical fluids: II. CO2, CH4, CO, O2and H2[J].GeochimicaetCosmochimicaActa, 1991, 55(11): 3191-3208.

[13] Schott G L. Shock-compressed carbon dioxide: Liquid measurements and comparisons with selected models[J].HighPressureResearch, 1991, 6(3): 187-200.

[14] Nellis W J, Mitchell A C, Ree F H, et al. Equation of state of shock-compressed liquds: Carbon dioxide and air[J].JChemPhys, 1991, 95: 5268-5272.

[15] 刘福生, 陈先猛, 陈攀森, 等. 液态CO2高温高密度状态方程研究[J]. 高压物理学报, 1998, 12(1): 28-33.

LIU Fu-sheng, CHEN Xian-meng, CHEN Pan-sen, et al. Equation of state of liquod CO2at highe temperatures and high densities[J].ChineseJournalofHighPressurePhysics, 1998, 12(1): 28-33.

[16] 徐士良. 常用算法程序集[M]. 北京: 清华大学出版社, 1995: 414.

[17] Ben-Amotz D, Herschbach D R. Estimation of effective diameters for molecular fluids[J].JournalofPhysicalChemistry,1990, 94(3): 1038-1047.

[18] Span R, Wagner W. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa[J].JournalofPhysicalandChemicalReferenceData, 1996, 25(6): 1509-1596.