多组元混合物状态方程*

施研博，赵艳红，刘海风，孟续军，王学容

(北京应用物理与计算数学研究所，北京 100094)

1 引 言

在高能量密度物理领域，常常会遇到因多介质、流体力学不稳定性等导致的物质混合，对此类现象进行流体力学或辐射流体力学模拟时，需要混合物的状态方程。在很多情况下，构成混合物的单质状态方程已知，而混合物的状态方程难以直接获得，此时采用等温等压条件及体积相加原理可以得到混合物的状态方程。徐锡申等人[1]指出：采用体积相加模型和等温等压假设，可以计算化合物、混合物及合金的状态方程；对于实际的物态方程，模型给出的方程组形式复杂，难以求解，可采用作图法计算混合物的分密度。然而，徐锡申等人并未给出具体的计算模型。王正言等[2]、唐鸽等[3]、王学容等[4]采用等温等压的热力学平衡条件和体积相加原理，针对两组元混合情况，计算了混合物的压力、内能和定容比热容。Cranfill[5]也给出了压力平衡、温度不一定平衡时混合物状态方程的计算方案，但是未给出热力学量的具体求解方法。

在实际工作中往往会遇到多于两种组元混合的情形，而且除了压强、内能和定容比热容外，有时还需要压强系数、等熵声速等其他热力学量。本工作基于等温等压的热力学平衡条件和体积相加原理，给出多组元混合物状态方程的理论模型，由此求解组元分密度及混合物的热力学量；采用该模型计算一种4组元钨合金的状态方程，并与其他理论计算结果进行对比，验证模型的有效性。

2 理论模型

在实际工作中，我们感兴趣的是物质在高温、高压状态下的性质。首先，假定混合物中各组元之间没有发生化学反应，从而能够很好地满足原子的体积相加原理[1]；其次，假定混合物中各组元之间达到热力学平衡，温度、压力处处相等。由此可以求得各组元的分密度，进而求得混合物的热力学量。

2.1 组元分密度

考虑单位体积的混合物，记混合物的密度为ρ，第k种物质的质量为mk，分密度为ρk，第k种物质的质量比定义为wk=mk/ρ。根据假设，混合物与各组元之间满足体积相加原理，得到

式中：n为组元数。由混合物各组元间的温度和压力相等假设，可知

联立求解n个方程，可以得到混合物各组元的分密度ρk。

2.2 热力学量求解

比内能e和定容比热容cV分别为

其中{(∂ρl/∂T)ρ}可由n个方程联立求解

(7)

式中：k=1,2,…,n-1。

由等温等压假定，混合物的压强p、压强系数β和等温声速cT可以通过第k种组元的压强求解

其中{(∂ρl/∂ρ)T}也由n个方程联立求解

式中：k=1,2,…,n-1。

根据热力学关系，由等温声速可得到等熵声速cS

至此，所需的热力学量计算完毕。所有热力学量都是由基本的热力学定律和关系式导出，自然满足热力学自洽性及稳定性条件[2]。

3 计算结果

编制了多组元混合物状态方程计算程序，计算了由4种组元构成的钨合金(W89Mo9Fe1Ni1)的状态方程。单质状态方程采用宽区实用状态方程[1]提供的状态方程库，该库还提供了钨合金W89Mo9Fe1Ni1的状态方程。

钨合金W89Mo9Fe1Ni1的冲击雨贡纽曲线如图1所示，图中比较了计算得到的状态方程与状态方程库给出的合金状态方程，其中ρ0为常压密度，TH为冲击雨贡纽温度。从图1可以看到，两种状态方程得到的压强和冲击雨贡纽温度具有很好的一致性。进一步比较由两种状态方程得到的冲击压力的相对差异(Δp/p)，如图2所示。可以看到：在常密度附近，Δp/p最高达到6%，这是由于在常温常密度状态附近，合金各组元的体积与体积相加假设偏离较大；在我们感兴趣的压缩区，Δp/p降到2%以下。

图1 钨合金W89Mo9Fe1Ni1的冲击雨贡纽曲线Fig.1 Hugoniot curve of tungsten alloy W89Mo9Fe1Ni1

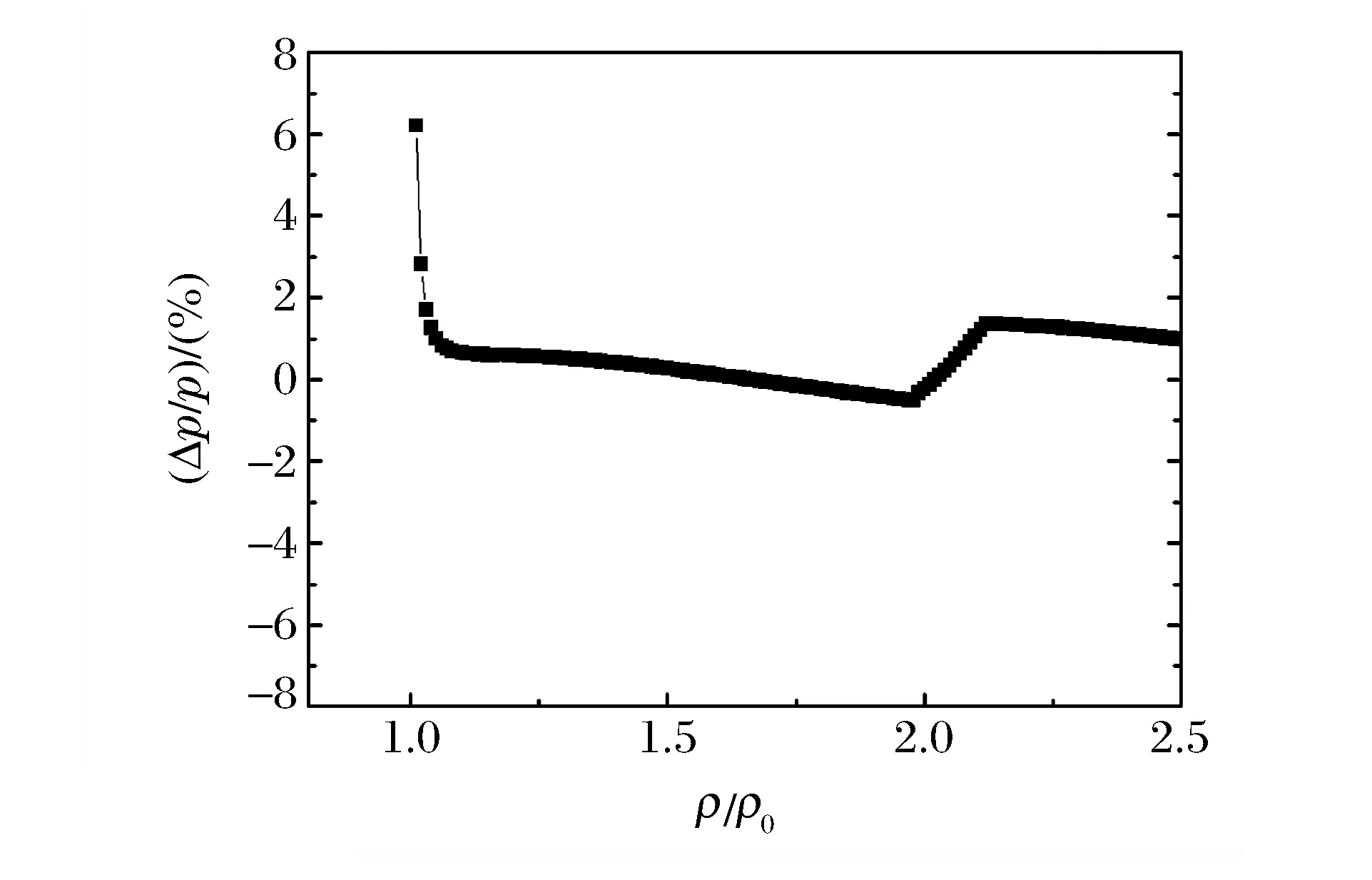
图2 两种状态方程得到的钨合金冲击压强的相对差异Fig.2 Relative difference of shock pressure obtained from two equations of state

图3显示了采用两种状态方程计算得到的压强和内能的相对差异(分别为Δp/p和ΔE/E)随密度变化的曲线。可以看到：对于压强，两者之间的相对差异小于2.5%；对于内能，相对差异小于1.5%。作为对照，图4显示了由混合物状态方程计算的钨合金压强和内能与纯钨之间的相对差异。可以看到，压强的相对差异大于11%，内能的相对差异大于4%。表明虽然合金的主要成分是钨，但其热力学性质与纯钨有一定的差别，本研究给出的理论模型可以区分这一差别。

图3 两种状态方程得到的钨合金压强和内能的相对差异Fig.3 Relative differences of pressure and internal energy obtained from two equations of state

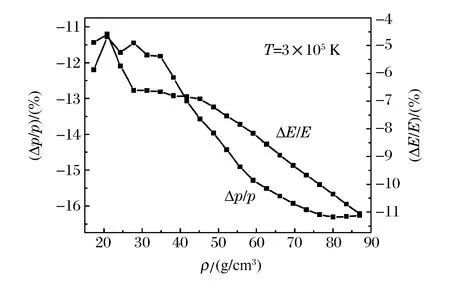
图4 钨合金和纯钨的压强和内能的相对差异Fig.4 Relative difference of pressure and internal energy obtained from tungsten alloy and pure tungsten

4 结 论

基于等温等压假设和体积相加原理，给出了由单质状态方程计算多种组元构成的混合物状态方程的理论方案，由此可以计算混合物的压强和内能，同时还可以得到定容比热容、压强系数、等温声速、等熵声速等热力学量。采用该混合物状态方程，计算得到了一种4组元钨合金的状态方程，所得结果与状态方程库直接给出的合金状态方程符合得很好，验证了物理方案及程序的正确性。

本方案可应用于在高温高压状态下能较好满足体积相加原理的多组元化合物、混合物及合金的状态方程计算。

[1] 徐锡申,张万箱.实用物态方程理论导引 [M].北京:科学出版社,1986:234.

XU X S,ZHANG W X.Introduction to theory of applied equations of state [M].Beijing:Science Press,1986:234.

[2] 王正言,李茂生,陈栋泉,等.混合物物态方程的体积相加模型和热力学自洽条件 [J].高压物理学报,1999,13(1):37-41.

WANG Z Y,LI M S,CHEN D Q,et al.Volume adding model and thermodynamic self-consistency for equation of state of mixtures [J].Chinese Journal of High Pressure Physics,1999,13(1):37-41.

[3] 唐 鸽,江少恩,易有根,等.混合物质高压状态方程的计算 [J].强激光与粒子束,2008,20(2):247-249.

TANG G,JIANG S E,YI Y G,et al.Calculation of equation of state of a material mixture under high pressure [J].High Power Laser and Particle Beams,2008,20(2):247-249.

[4] 王学容,王建国.混合物物态方程的计算 [J].强激光与粒子束,2011,23(8):2083-2089.

WANG X R,WANG J G.Calculation of equation of state of material mixture [J].High Power Laser and Particle Beams,2011,23(8):2083-2089.

[5] CRANFILL C W.EOS of a material mixture in pressure equilibrium:LA-13661 [R].Los Alamos:Los Alamos National Laboratory,2000.