爆炸波问题中偶然不确定度的量化*
梁 霄,王瑞利
(1.北京应用物理与计算数学研究所,北京 100094;2.山东科技大学数学与系统科学学院,山东青岛 266590)
1 引 言
基于建模与模拟(Modeling and Simulation,M&S)的设计可以明显缩短产品研发周期、降低其生产成本,在生产和研发过程中起着重要的作用,尤其是试验成本很高、风险很大和危害人身安全的研究领域。如何提高建模的逼真度及模拟结果的精度,从而通过物理或者数学模型模拟客观世界及其演变过程,已成为一个亟待解决的重要问题[1-8]。
研究者总是希望M&S方法能够对研究客体进行逼真的刻画和精确的描述,然而,实际研究过程中,误差和不确定度的存在是不可避免的[8]。 特别是对于一些复杂的非线性系统,初值或边值的微小差异有时会引起模拟结果剧烈的变化,影响模型的预测效果。M&S方法的关键任务之一就在于掌握误差与不确定度的规律,通过采用比较完善的M&S技术,使用更加可靠的算法,将不确定度和误差减小到最低限度。为了达到这一目的,分析M&S不确定度的来源及其性质是非常重要的。了解不确定度对计算结果的影响,可以确定最终结果的可信度。
不确定度量化(UQ)是一门蓬勃发展的学科。美国非常重视UQ技术的研究,近几年一直将UQ技术作为数值模拟软件及其应用研究的重点。1991年暂停地下核试验后,美国为了维持武器库的水平与能力,保证武器的可靠性,开展了先进模拟和计算计划,进一步刺激了UQ的发展。另外,2001年隶属于美国能源部的三大国家核武器安全实验室(SNL,LANL,LLNL)共同倡导将UQ方法应用于核武器库存安全管理,给出了认知不确定度和偶然不确定度在反应堆故障排除和放射性核废料处理中的应用案例[9-11]。本研究以爆炸波问题为例,利用非嵌入多项式混沌方法进行偶然不确定度的量化,并将结果与Monte Carlo(MC)所得结果比较,以期为非嵌入多项式系统不确定度的量化提供参考。
2 不确定度的分类和量化方法
如图1所示,不确定度一般分为偶然不确定度和认知不确定度。偶然不确定度是由于事物固有的随机性而引起的,有时也称为可变性和随机不确定性,是系统固有的特点,即使在理论上也不能约减,如火箭助推器系统中质量特性和几何形状的变异。目前对偶然不确定度的数学描述是采用概率论的方法,给出输出量的概率描述。增加数据的样本容量有助于更准确地确定样本的分布类型,但并不会减小不确定度。认知不确定度是由于缺乏知识导致的不确定度,有时也称为知识的不确定性、模型形式的不确定性或主观不确定性。认知不确定度分两类:一类是认可不确定度,即所谓“知道的不知道”,来源于对物理现象的理解较差,如断裂力学; 另一类是盲目不确定度,即所谓“不知道的不知道”,例如软件中的程序代码出错[8]。
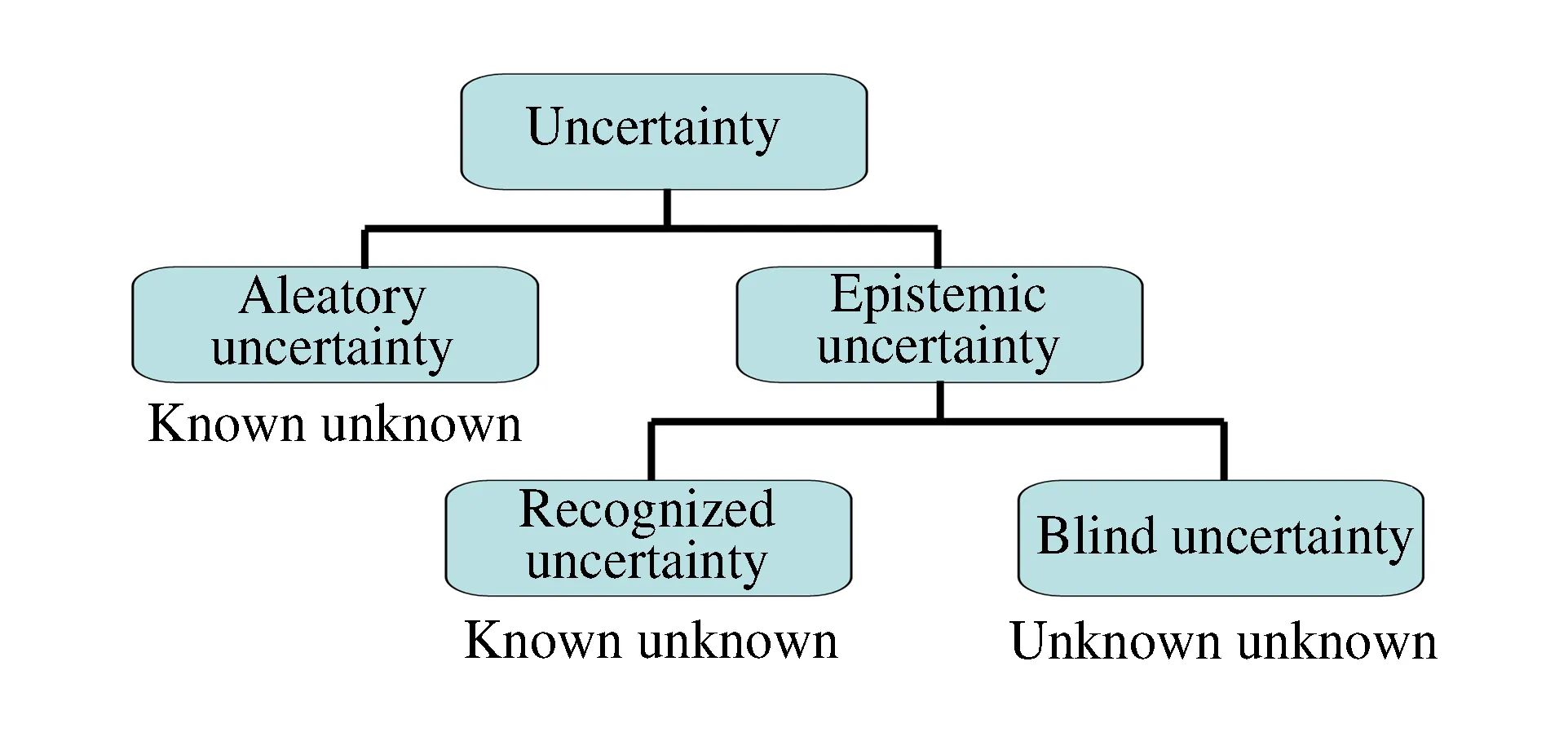
图1 不确定度分类Fig.1 Classification of uncertainty
不确定度量化方法是利用各种数学和统计学方法,对随机因素或认知缺陷尽可能地给出分布或区间描述,建立M&S中偶然或认知不确定性因素与系统响应量之间的关系,进而量化影响系统性能的不确定性,给出系统响应量性能分析的不确定度度量方法。
在计算流体力学和计算固体力学领域中,不确定度量化的概念和方法发展迅速[8]。许多方法都可以应用于偶然不确定度的量化,其中敏感度分析方法、抽样方法、代理模型方法、随机微分方程方法、参数率定与优化方法已经应用于复杂工程中。MC方法是出现最早、应用最广泛的一种抽样方法,并且使用直接,不需要任何假设,可以得出模型在不确定意义下的精确解,通常作为基准解[12]。但是MC方法的计算成本过高,还会遇到维数灾难问题,因此人们已经开始寻找MC的替代方法,如随机谱方法。
随机谱方法是使用谱逼近随机微分方程或参量,然后将其分解为独立的确定性分量和随机分量来量化不确定性。其数学思想是数学模型中的每一个参量利用正交多项式(如Hermite多项式)展开成无穷级数项,在实际应用中取有限项[13-15]。根据求解系数方法的不同,将多项式混沌分为嵌入多项式混沌(Intrusive Polynomial Chaos,IPC)和非嵌入多项式混沌(Non-Intrusive Polynomial Chaos,NIPC)。IPC无法利用已有程序,需要对已有的数值求解程序进行大量修改或者重新编制计算程序。
3 非嵌入多项式混沌方法
NIPC是把已有的数值求解程序作为一个黑匣子,在随机空间里通过一定的抽样方法获得若干个样本点,将样本点输入到确定性程序求解,然后对确定性输出结果进行统计分析,以获得相关数值求解结果的统计特征,进而评估输入参数或计算条件的不确定性在计算过程中传播的影响。NIPC采用已有的数值模拟程序,不需要对控制方程进行修改,不需要重新编写程序。
NIPC不确定度评估的计算流程如下。
(1) 选取参数λ服从何种分布。
(2) 利用相应标准随机变量,确定参数λ多项式混沌谱展开,如λ(ξ)=λ0+sξ。
(3) 对参数构成的随机变量ξ进行抽样{θ1,θ2,…,θM+1},将其带入参数λ多项式混沌谱展开式中,得到参数λ的抽样{ω1,ω2,…,ωM+1},对每一次抽样,模型参数值为确定值ωj,j=1,…,M+1。
(4) 对每个抽样确定后的模型参数值,利用确定性程序(例如CFD程序)计算得到相应的数值解u(x,t),如第j次抽样得到解为[u(x,t)]j。
(1)式可采用众多积分公式求出,例如:假定正交多项式归一,采用Latin等概率抽样,则
(2)
4 偶然不确定度量化在爆炸波问题中的应用
4.1 爆炸波问题的控制方程和迎风格式
一维Lagrange坐标系中爆炸波问题的控制方程为[16]
(3)
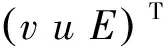
(3)式也可以写成非守恒形式
(4)
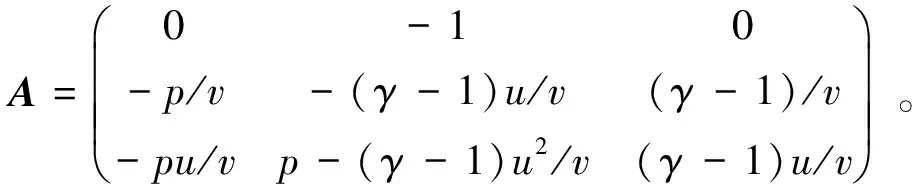
4.2 爆炸波初边值问题的不确定度量化
与Lax和Sod问题类似,爆炸波问题也是一种激波管问题。根据炸药PBX9401的特性,将初始状态等效于炸药爆轰波CJ状态,建立一维平面模型:在无限长管道中,以x=0为界,左侧是炸药,采用高压气体模型描述,右侧是低压气体。初始时刻,两侧物质均处于静止状态,中间用薄膜隔离。t=0时刻,薄膜发生破裂,产生左行稀疏波和右行激波。假设该爆炸波问题的计算区域为[-1,1],初值条件如下:在x≤0区域,炸药密度ρL服从期望μ为1.4 g/cm3、标准差σ为5.0×10-4g/cm3的正态分布,速度uL=-2.6 km/s,压强pL=37.18 GPa,多方指数γL=3.1;在x>0区域,气体密度ρR=15.3 g/cm3,速度uR=0,压强pR=1.0 GPa,多方指数γR=1.4。
该问题的特点是左、右两侧气体的多方指数不同,属于多介质激波管问题,并且有解析解[17]。该问题的解析解表明,强间断横跨激波面和激波后有一个窄的密度峰,可以用于验证流体力学程序的计算能力和格式精度。对于左端炸药密度,由于加工过程中炸药颗粒凝结的不均匀性,其密度存在随机性。假设炸药密度的概率密度函数(PDF)为
(5)
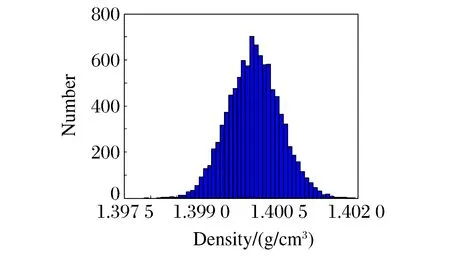
图2 炸药密度分布直方图Fig.2 Histogram of explosive density distribution
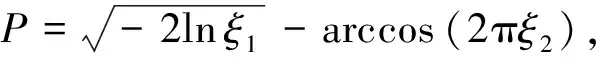
确定型爆炸波方程通常使用数学模型的单一解描述。对于不确定系统,这是不现实的,实际上需要执行一系列运算评估模型中输入不确定度对输出不确定度的影响,即不确定度传播。确定型方程利用迎风格式,计算到T=0.10时刻,得到1 000组状态响应量构成的“马尾图”。计算结果的信息量巨大,必须对其量化以提取有用的信息。
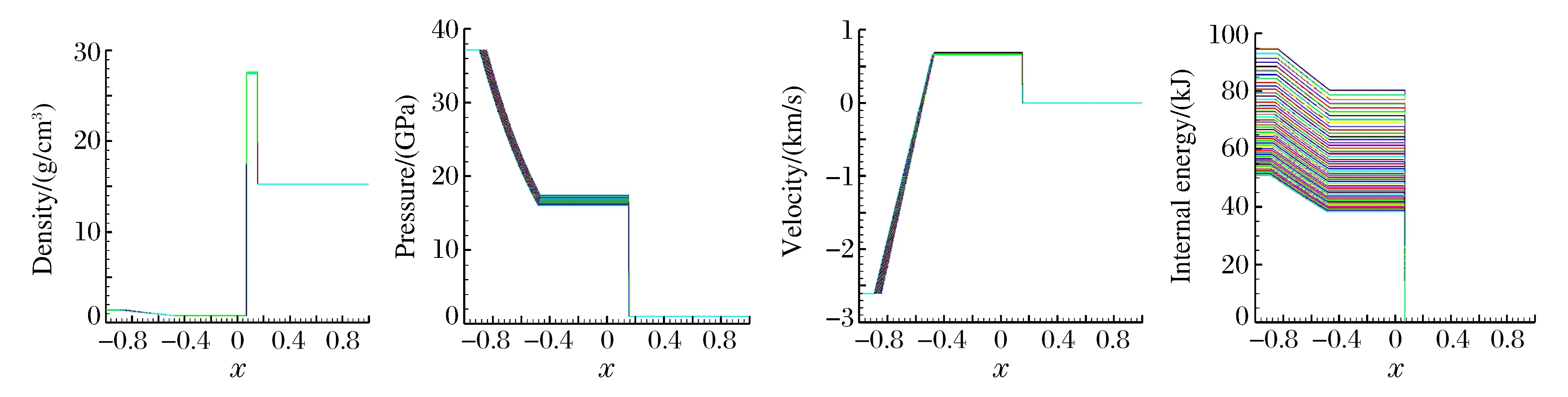
图3 1 000组抽样下爆炸波问题的计算结果Fig.3 Results of blast wave problem solved with 1 000 times sampling by NIPC method
4.3 爆炸波问题的不确定度传播
采用NIPC和MC方法对爆炸波初值问题开展不确定度的量化,得到T=0.10时刻计算区域中密度、压力、速度、能量的期望和标准差如图4所示,其中E为期望,σ为标准差。由图4可知,MC方法和NIPC方法吻合较好,说明NIPC应用于不确定度量化分析是可行的。
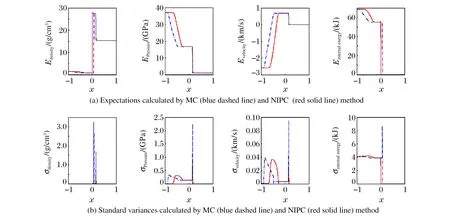
图4 T=0.10时刻爆炸波问题中密度、压强、速度和能量的期望与标准差Fig.4 Expectations and standard variances of density,pressure,velocity and internal energy in blast wave problem at T=0.10
4.4 激波位置的概率密度函数
为进一步验证NIPC方法的有效性,利用NIPC方法研究初边值输入不确定度对爆炸波问题激波位置的影响,计算得到T=0.10时刻激波位置的概率密度函数,如图5所示。可以看出,激波位置近似服从正态分布,激波位置的期望为0.19,标准差为4.13×10-4。图6为采用MC方法取样106次与采用NIPC取样103次计算所得激波位置的概率密度函数,通过对比可以看出,MC方法的概率密度函数和NIPC方法得到的概率密度函数基本吻合,说明了NIPC方法的可靠性和有效性。
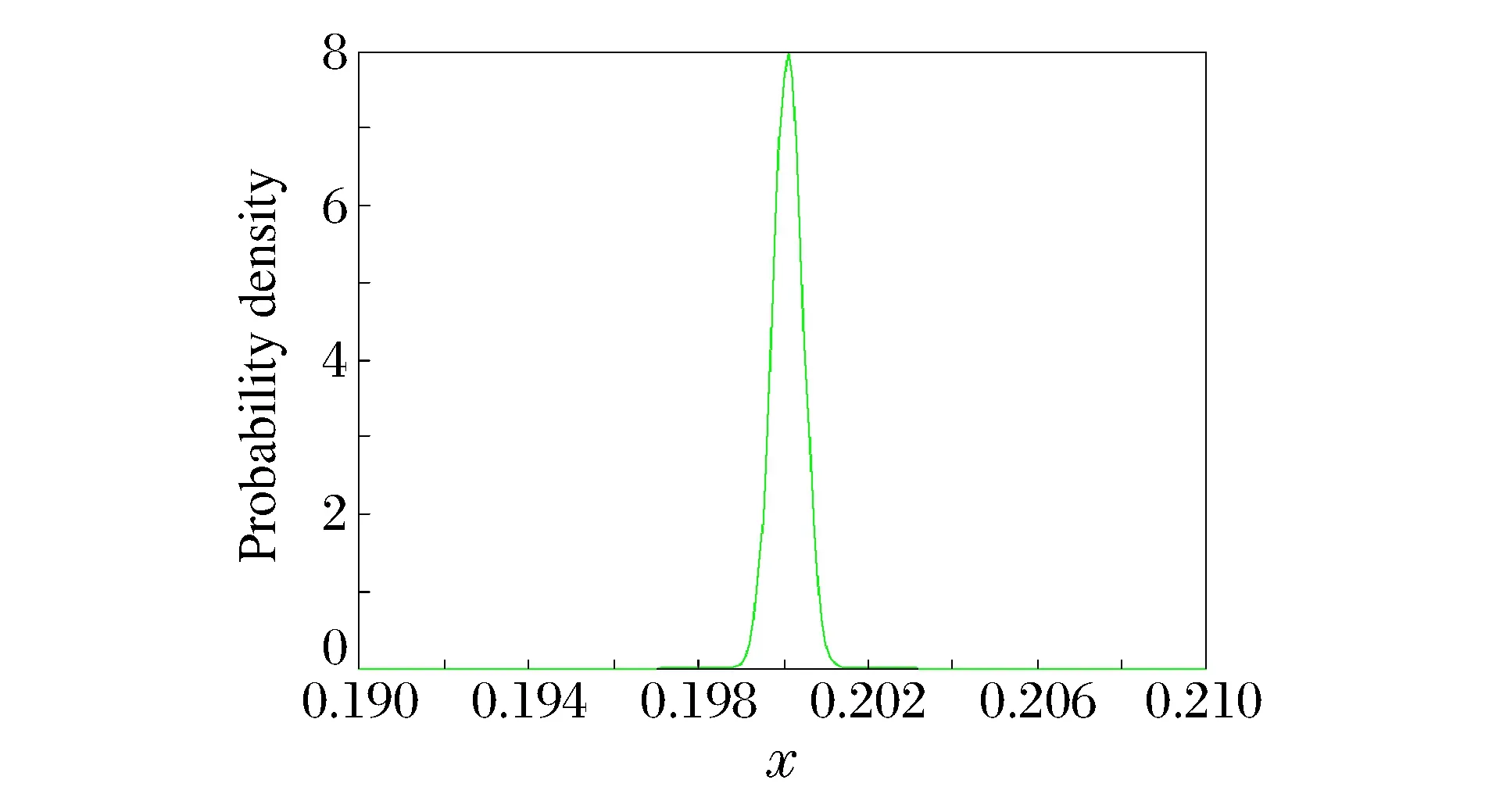
图5 激波位置的概率密度分布函数Fig.5 Probability density funtion of shock wave position by NIPC at T=0.10
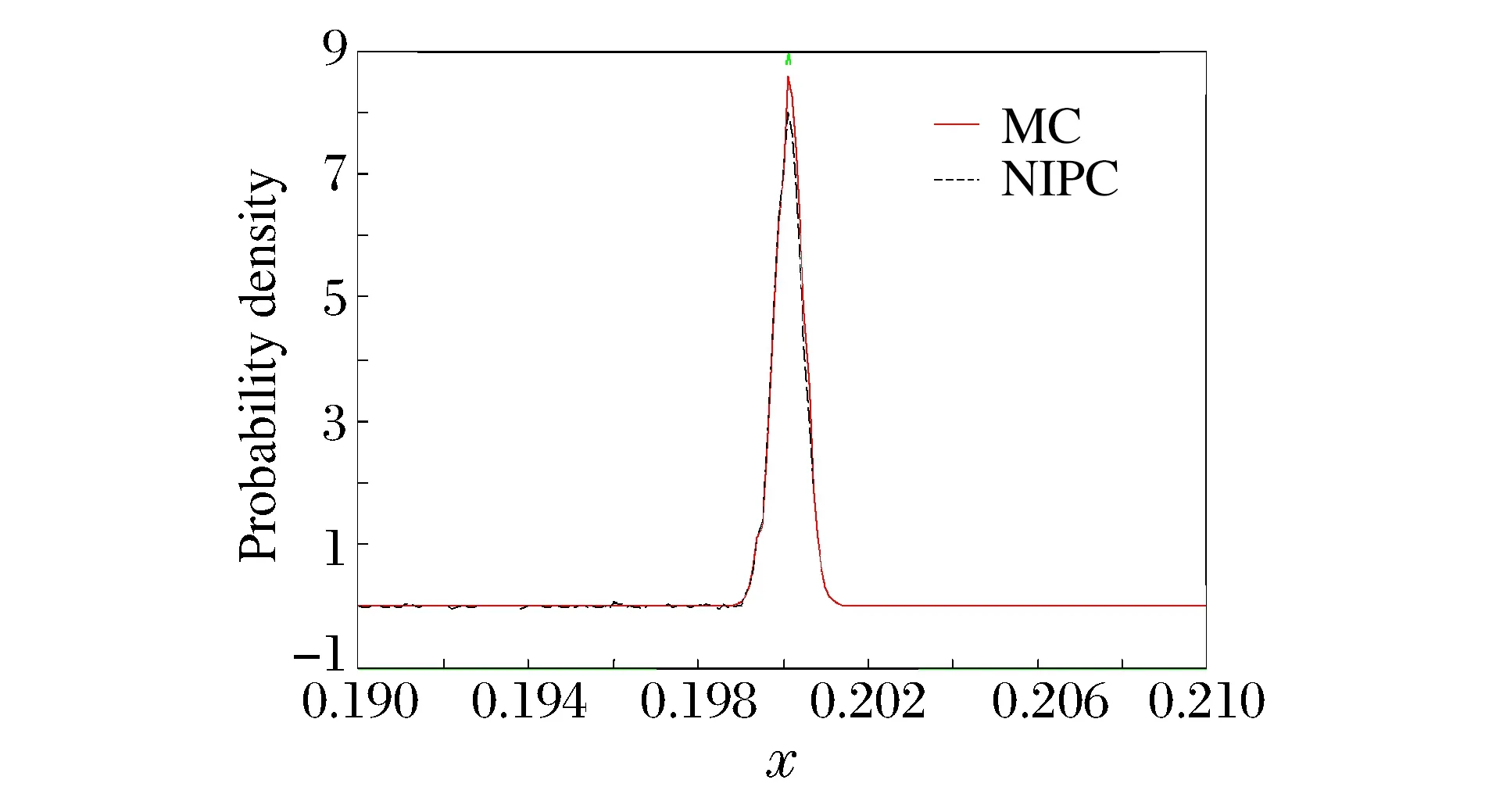
图6 激波位置的概率密度分布函数Fig.6 Comparison of probability density funtion of shock wave position by MC and NIPC at T=0.10
5 结 论
给出建模中输入初边值偶然不确定度抽样方法及量化结果,并利用MC和NIPC方法计算得到偶然不确定度对输出结果期望、标准差及激波位置的影响,验证了NIPC方法在偶然不确定度量化方面的有效性。 此方法对复杂工程M&S中偶然不确定度量化具有重要的参考价值。
[1] 杨振虎.假设检验与CFD不确定度量化分析 [J].航空计算技术,2003,33(2):5-8.
YANG Z H.Hypothesis tests and analysis of CFD uncertainty quantification [J].Aeronautical Computer Technique,2003,33(2):5-8.
[2] 王瑞利,江 松.多物理耦合非线性偏微分方程与数值解不确定度量化数学方法 [J].中国科学A辑,2015,45(5):723-728.
WANG R L,JIANG S.Mathematical methods for uncertainty quantification of the nonlinear partial differential equation and numerical solution [J].Science China Series A,2015,45(5):723-728.
[3] 刘 全,王瑞利,林 忠,等.流体力学拉氏程序收敛性及数值计算不确定度初探 [J].计算物理,2013,30(3):346-352.
LIU Q,WANG R L,LIN Z,et al.Asymptotic convergence analysis and quantification of uncertainty in Lagrangian computation [J].Chinese Journal of Computational Physics,2013,30(3):346-352.
[4] 王瑞利,刘 全,温万治.非嵌入式多项式混沌法在爆轰产物JWL参数评估中的应用 [J].爆炸与冲击,2015,35(1):9-15.
WANG R L,LIU Q,WEN W Z.Uncertainty quantification for JWL EOS parameters using non-intrusive polynomial chaos [J].Explosion and Shock Waves,2015,35(1):9-15.
[5] 唐 炜,王玉明.复杂系统关键特征参数确定方法 [J].信息与电子工程,2011,9(1):83-86.
TANG W,WANG Y M.A method of confirming critical characteristic parameters for complex system [J].Information and Electrical Engineering,2011,9(1):83-86.
[6] 陈坚强,张益荣.基于Richardson插值法的CFD验证和确认方法的研究 [J].空气动力学学报,2012,30(2):176-183.
CHEN J Q,ZHANG Y R.Verification and validation in CFD based on the Richardson extrapolation method [J].Acta Aerodynamical Sinica,2012,30(2):176-183.
[7] 刘 全,王瑞利,林 忠.非嵌入多项式混沌方法在拉氏计算中的应用 [J].固体力学学报,2013,33(增刊):224-233.
LIU Q,WANG R L,LIN Z.Uncertainty quantification for Lagrangian computational using non-intrusive polynomial chaos [J].Chinese Journal of Solid Mechanics,2013,33(Suppl):224-233.
[8] 张 楠,沈泓萃,姚惠之.阻力和流场的CFD不确定度分析探讨 [J].船舶力学,2008,12(2):211-224.
ZHANG N,SHEN H C,YAO H Z.Uncertainty analysis in CFD for resistance and flow field [J].Journal of Ship Mechanics,2008,12(2):211-224.
[9] OBERKAMPF W,ROY C.Verification and validation in the scientific computing [M].New York:Cambridge University Press,2010.
[10] 马智博,郑 淼,尹建伟,等.爆轰模拟不确定度的量化方法 [J].计算物理,2011,28(1):66-74.
MA Z B,ZHENG M,YIN J W,et al.Quantification of uncertainties in detonation simulations [J].Chinese Journal of Computational Physics,2011,28(1):66-74.
[11] HELTON J,JOHNSON J,SALLABERRY C,et al.Survey of sampling-based method for uncertainty and sensitivity analysis [J].Reliab Eng Syst Safe,2006,91(11):1175-1209.
[12] HELTONl J,JOHNSON J,SALLABERRY C.Quantification of margins and uncertainties:example analyses from reactor safety and radioactive waste disposal involving the separation of aleatory and epistemic uncertainty [J].Reliab Eng Syst Safe,2008,99(1):175-195.
[13] JANSSEN H.Monte-Carlo based uncertainty analysis:sampling efficiency and sampling convergence [J].Reliab Eng Syst Safe,2013,109:123-132.
[14] 皮 霆,张云清,吴景铼.基于多项式混沌方法的柔性多体系统不确定性分析 [J].中国机械工程,2011,22(19):2341-2348.
PI T,ZHANG Y Q,WU J L.Uncertainty analysis of flexible multibody systems using the polynomial chaos methods [J].China mechanical Engineering,2011,22(19):2341-2348.
[15] 王晓东,康 顺.多项式混沌方法在随机方腔流动模拟中的应用 [J].中国科学E辑,2011,41(6):790-798.
WANG X D,KANG S.Application of polynomial chaos on numerical simulation of stochastic cavity flow [J].Science China Series E,2011,41(6):790-798.
[16] CHEN Q,GOTTLIEB D,HESTHAVEN J.Uncertainty analysis for the steady state flows in a dual throat nozzle [J].J Comput Phys,2005,204:119-148.
[17] 水鸿寿.一维流体力学差分方法 [M].北京:国防工业出版社,1998.
SHUI H S.The difference method of one dimensional fluid mechanics [M].Beijing:National Defense Press,1998.

