弹体侵彻混凝土开坑阶段阻力的计算*

薛建锋，沈培辉，王晓鸣

(南京理工大学机械工程学院，江苏南京 210094)

1 引 言

为了研究侵彻过程中弹体所受阻力的变化情况，需要对弹头表面在开坑区的侵彻阻力进行清晰的描述。鉴于Forrestal方法的不足，本研究基于应力波损伤理论，对混凝土材料开坑区的侵彻特性进行分析，利用应力波反射形成层裂阐述靶面成坑机理，并根据侵彻阻力做功的简化等效阻力线得到新阻力模型，将理论结果与数值模拟和实验结果比较，得出开坑阶段阻力计算新方法的适用范围。

2 Forrestal半经验法[2-3]

大量混凝土靶侵彻实验表明，混凝土材料的侵彻通道可分为开坑区和贯穿孔洞区。Forrestal假设：在开坑区的4R(R为弹体半径)深度内，侵彻阻力随侵彻深度增大而线性增大；当侵彻深度大于4R以后，侵彻阻力与侵彻深度的关系可以采用空腔膨胀理论描述，即侵彻阻力F的表达式为

(1)

式中：C为侵彻阻力系数；W为侵彻深度；B为动阻力项系数，B=1；S为靶体静态阻力系数；fc为混凝土材料的单向无侧限抗压强度；N为头部形状因子；ρ为混凝土密度；v为弹体速度。其中，侵彻阻力系数C和头部形状因子N的表达式为

式中：m为弹体质量；v0为弹体初始速度；v1为开坑结束时的弹体速度；ψ为曲径比。当侵彻深度等于4R时，开坑阶段恰好结束，根据连续性条件，由(1)式计算可得，此时的弹体速度为

(4)

3 理论模型

3.1 开坑过程描述

开坑区是撞击应力波引起表层混凝土材料损伤破坏形成的。冲击应力波在混凝土靶的自由表面反射形成拉伸波，在临近自由表面的位置造成相当高的拉应力，一旦满足最大拉应力瞬时断裂准则，就会在该处引起材料的破坏；当裂口足够大时，整块裂片携带着传入其中的动量从靶体飞离；出现层裂后，靶体表面形成新的自由面，继续入射的应力波在新自由表面上反射，造成第2层层裂；以此类推，混凝土表面逐渐被破坏，形成开坑区。

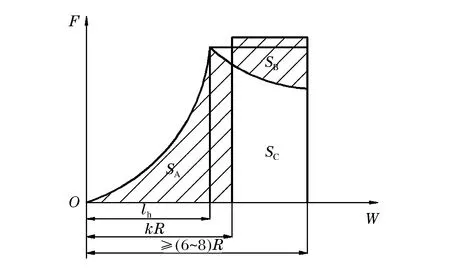
图1 简化等效阻力曲线Fig.1 Simplified equivalent resistance line

开坑深度与弹体直径有关，一般认为开坑深度为弹体直径的2倍。根据文献[13]可知，应力波在混凝土表层造成损伤的深度应该比开坑区的深度还要大，即应力波损伤的深度将大于(6～8)R。应力波在混凝土材料内的传播速度远大于弹体运动速度，因此当弹体侵彻混凝土靶一定深度后产生的应力波能量足够大，足以损伤和破坏弹体运动前方的混凝土表层，造成混凝土表层材料强度下降，从而使得开坑区混凝土对弹体阻力的下降。考虑应力波对混凝土表层的损伤和破坏，在开坑区，简化等效阻力线由0～kR区间的零阻力线和kR以后的满阻力线构成，如图1所示。为保证开坑区侵彻效应近似等效，要求简化等效阻力线做功与真实阻力线做功近似相等，即两阴影区域SA和SB的面积相等。

3.2 阻力计算

弹体头部表面的应力为

(5)

式中：psd≈2(1-lnα)σsd/3，其中σsd为混凝土材料的动态屈服强度，α=1-(ρ/ρp)，ρp为混凝土的锁变密度；C=BNρ，其中动阻力项系数B的表达式为

经典框架有很多种形式的推广, 例如连续框架[4]、算子值框架[5]、G-框架[6]、子空间框架[7]、 Banach框架[8]、Hilbert C*-模框架[9]等。文献[10]对经典框架的等式与不等式做了深入的研究。本文在文献[11-12]的基础上, 用算子理论的方法对Rd上的测度框架进行进一步的研究。

(6)

混凝土材料综合动态强度参数的公式为

(7)

式中：Wmax为最大侵彻深度。在开坑区，弹头的轴向阻力可表示为

(8)

图2 弹头参量示意图Fig.2 Warhead parameters

式中：r为曲率半径，μ为摩擦系数，φ0为弹头侵彻的初始角度，φ为侵彻过程中的角度，如图2所示。

根据能量守恒定理可知，由于阻力的作用，侵彻过程中弹体的动能减小。根据动能定理，弹体减小的动能等于开坑阶段阻力和开坑深度的乘积，即

(9)

根据3.1节中分析，取k≈4时，即有SA≈SB，此时弹体的阻力模型由(1)式变为

(10)

将W(t=0)=4R、v(t=0)=v0两个初始条件与(10)式联立求解，得到最大侵彻深度的计算公式为

(11)

4 数值模拟及实验研究

为了验证理论模型的可靠性和正确性，进一步采用数值模拟和实验方法研究开坑过程中侵彻深度与阻力之间的关系。

4.1 有限元模型

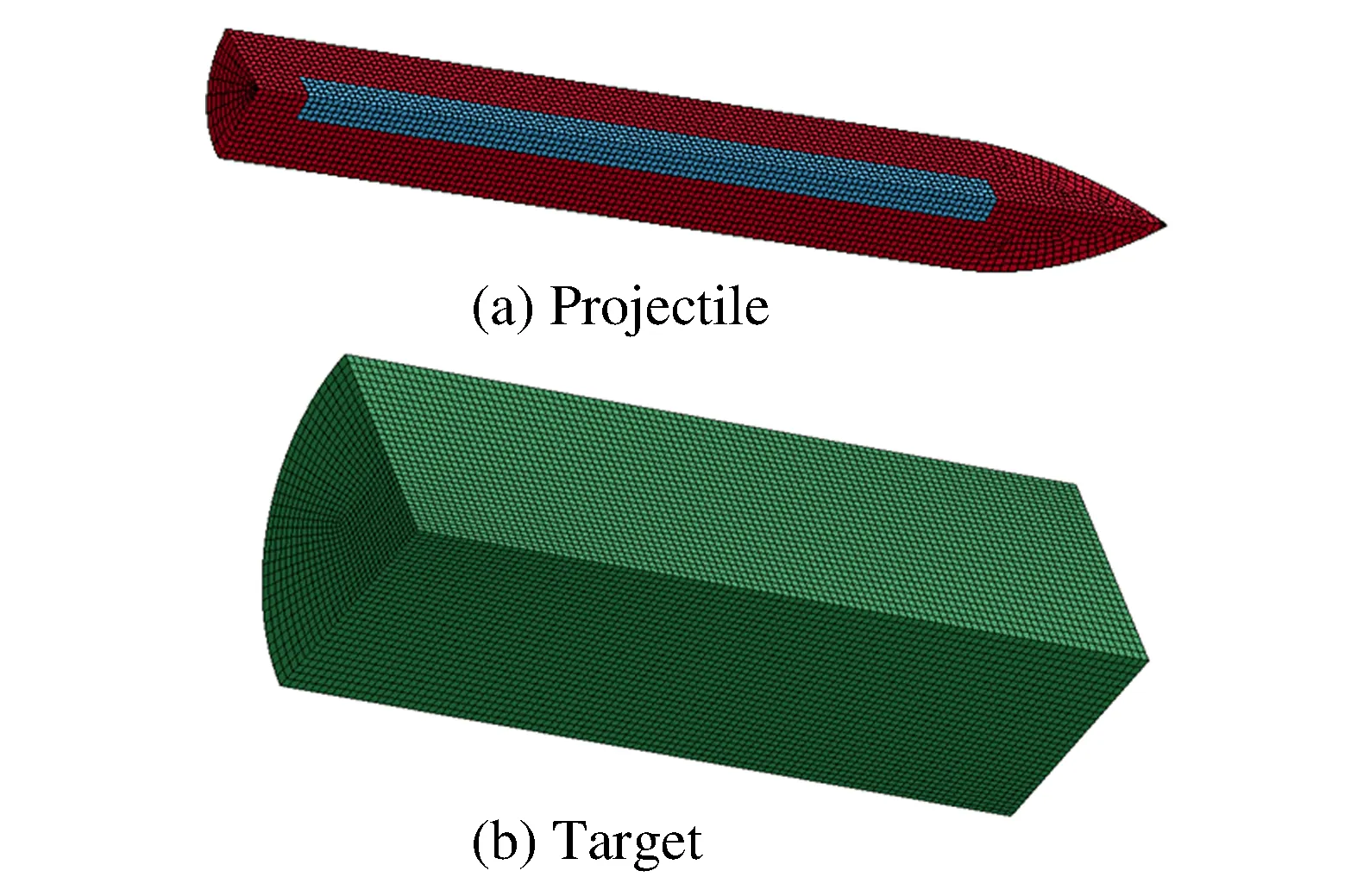
图3 弹靶有限元网格Fig.3 Finite element model

利用ANSYS-DYN软件建立弹体侵彻混凝土靶的有限元模型如图3所示。弹体的直径为10 mm，长度为70 mm，头部曲率半径为3或4。为消除侧面约束对侵彻的影响，将混凝土靶设置为半无限靶，直径为300 mm，高度为400 mm。考虑到弹体结构和载荷的对称性，为节省计算时间，采用实体模型的1/4进行建模和求解。在弹体经过靶板区域20 mm的范围内，网格比较密集，其他区域网格较稀疏。对弹体和靶体对称面上的节点设置对称约束，并对靶侧面施加边界条件，以模拟靶体被固定的情况。

弹体采用刚性模型描述，弹体密度为7.83 g/cm3，弹性模量为204 GPa，泊松比为0.3。弹体内装填物视为各向同性弹塑性材料，其密度为1.8 g/cm3，弹性模量为5 GPa，泊松比为0.4，采用弹塑性材料模型描述。在弹体斜侵彻混凝土靶的过程中，弹体与混凝土靶板之间选择LS-DYNA中的面面接触算法。混凝土靶满足Grüneisen状态方程，其强度模型采用HJC累积损伤材料模型，具体材料参数如表1所示。其中G为剪切模量，A1为内聚力强度，B1为压力强化系数，C1为应变率敏感系数，N1为压力硬化系数，T为混凝土的最大拉伸强度，D1和D2是混凝土损伤参数，εfmin为混凝土的最小塑性应变，p1为静水压力。

表1 混凝土材料参数Table 1 Concrete material parameters

4.2 实验方法

图4为P3型和P4型两种弹体的实物图，其曲率半径分别为3和4，弹身直径均为10 mm，长径比为7，弹体材料为35CrMnSi高强度合金钢，通过改变弹体内部开孔深度，确保弹体质量为80 g。图5为混凝土靶的实物图，靶板直径为300 mm，为弹径的30倍，因此可以忽略靶板的横向边界效应。为了方便浇注混凝土靶，并保证侵彻后靶体的完整性，靶板外围采用3 mm厚的钢圈加固。弹体速度通过改变装药量控制，并通过锡箔纸和双通道测时仪进行测量，现场布置如图6所示。

图4 两种型号弹体实物图Fig.4 Photos of projectiles

图5 混凝土靶Fig.5 Concrete target

图6 实验布局Fig.6 Experimental setup

4.3 实验结果

图7为实验后开坑区的破坏效果。由图7可知，侵彻后靶体正面开坑呈漏斗形，形成了相对于弹着点基本对称的弹坑区。靶面无明显裂纹，说明边界约束对侵彻过程几乎没有影响。开坑区的几何参数如表2所示。从表2可以看出，弹坑深度为弹体直径的3～4倍，并且随着弹体侵彻速度的增加，弹坑面积逐渐增加，弹坑深度也发生明显的变化。

图7 开坑区破坏效果Fig.7 Photos of concrete damage

表2 开坑区的几何参数Table 2 Geometrical parameters of crater zone

5 结果分析

5.1 数值模拟结果分析

图8为数值模拟中计算时间为20和95 μs时靶体的损伤效果。从图8中可以看出，开坑阶段，混凝土发生了层裂和挤兑，并且靶体表面的开坑形状与实验结果(见图7)一致。弹体撞击混凝土靶时，弹体周围的压力远远超过了混凝土材料的屈服强度，弹体和靶体内部均产生强平面冲击波，由于靶体表面的反射，平面波发生变形，并且在弹靶交界面上发生反射，使得在反射波后有许多靶体碎块从靶体内部向外飞出；之后，随着弹体的深入，在反射波和压缩波的共同作用下，更多的碎块从靶体内飞出，靶体表面形成漏斗坑；最终，弹头全部进入靶体，不再产生靶面剥落。

图8 开坑阶段数值模拟结果Fig.8 Simulation results of cratering stage

5.2 模型的对比分析

Forrestal半经验公式假设开坑深度为弹径的2倍，而实验中P4和P3弹体的开坑深度均大于2倍的弹径。根据新模型计算弹体在开坑过程中所受的阻力，进而求得不同开坑速度时的开坑深度，并将结果与Forrestal半经验公式、数值计算和实验结果进行比较，如图9所示。从图9中可以看出，数值模拟和实验结果与新模型预测值吻合较好。开坑阶段结束后，P3弹体的速度分别为835、724和676 m/s，开坑阶段消耗的动能分别占弹体初始动能的20.6%、21.8.%和16.1%；而开坑阶段结束后，P4弹体的速度分别为793、734和687 m/s，消耗的动能占弹体初始动能的22.2%、20.3%和19.5%。由于开坑阶段弹体消耗的动能占弹体初始动能的比例较大，因此弹体在开坑区侵彻阻力的准确表达式对了解弹体的剩余侵彻能力以及之后侵彻过程的分析很有意义。

图9 开坑深度与侵彻速度的关系Fig.9 Relation of penetration depth and velocity

6 结 论

根据半经验公式对开坑区的阻力进行计算，从应力波表层损伤理论和反射形成层裂角度解释了混凝土开坑的机理，利用侵彻阻力做功等效的方法建立了开坑区阻力计算的新模型。经验证，数值模拟和实验结果与理论模型计算结果吻合较好，新模型能够较好地描述弹体在开坑阶段阻力与速度的关系，适用于弹体侵彻混凝土靶或部分以混凝土为面层的多层复合靶的侵彻计算。

[1] 吴 昊,方 秦,龚自明,等.应用改进的双剪强度理论分析岩石靶体的弹体侵彻深度 [J].工程力学,2009,26(8):216-222.

WU H,FANG Q,GONG Z M,et al.Analysis on penetration depth of projectiles into rock targets based on the improved twin shear strength theory [J].Engineering Mechanics,2009,26(8):216-222.

[2] FORRESTAL M J,ALTMAN B C,CARGILE J D,et al.An empirical equation for penetration depth of ogive-nose steel projectiles into concrete targets [J].Int J Impact Eng,1994,15(4):395-405.

[3] FORRESTAL M J,FREW D J,HANCHAK S J,et al.Penetration of grout and concrete targets with ogive-nose steel projectile [J].Int J Impact Eng,1996,18(5):465-476.

[4] FORRESTAL M J,FREW D J,HICHERON J P,et al.Penetration of concrete targets with deceleration time measurement [J].Int J Impact Eng,2003,28(5):479-497.

[5] FREW D J,HANCHAK S J,GREEN M L,et al.Penetration of concrete targets with ogive-nose rods [J].Int J Impact Eng,1998,21(6):489-497.

[6] QIAN L X,YANG Y,LIU T.A semi-analytical model for truncated-nose projectiles penetration into semi-infinite concrete targets [J].Int J Impact Eng,2000,24(9):947-955.

[7] 沈河涛.弹丸侵彻混凝土效应研究 [D].北京:北京理工大学,1996.

SHEN H T.Research on the effect of projectile penetration into concrete [D].Beijing:Beijing Institute of Technology,1996.

[8] BACKMAN M E,GOLDSMITH W.The mechanics of projectiles into targets [J].Int J Eng Sci,1978,16(1):1-99.

[9] 刘海鹏,高世桥,金 磊,等.弹侵彻混凝土靶面成坑的分阶段分析 [J].兵工学报.2009,30(增刊2):52-56.

LIU H P,GAO S Q,JIN L,et al.Phase analysis on crater-forming of projectile penetrating into concrete target [J].Acta Armamentarii,2009,30(Suppl 2):52-56.

[10] CHEN X W,FAN S C,LI Q M.Oblique and normal perforation of concrete targets by a rigid projectile [J].Int J Impact Eng,2004,30(6):617-637.

[11] 柴传国,皮爱国,武海军,等.卵形弹体侵彻混凝土开坑区侵彻阻力计算 [J].爆炸与冲击,2014,34(5):630-635.

CHAI C G,PI A G,WU H J,et al.A calculation of penetration resistance during cratering for ogive-nose projectile into concrete [J].Explosion and Shock Waves,2014,34(5):630-635.

[12] 彭 永,方 秦,吴 昊,等.对弹体侵彻混凝土靶体阻力函数计算公式的探讨 [J].工程力学,2015,32(4):112-199.

PENG Y,FANG Q,WU H,et al.Discussion on the resistance forcing function of projectiles penetrating into concrete targets [J].Engineering Mechanics,2015,32(4):112-119.

[13] 王成华,史利平,徐孝诚.混凝土靶侵彻计算的半经验法 [J].强度与环境,2007,34(2):31-37.

WANG C H,SHI L P,XU X C.Semi-empirical method of penetration into concrete targets [J].Structure Environment Engineering,2007,34(2):31-37.