基于量纲分析的平面冲击波经验模型研究*
赵传荣,孔德仁
(1.南京理工大学机械工程学院,江苏南京 210094; 2.安徽工业大学电气与信息工程学院,安徽马鞍山 243032)
1 引 言
平面冲击波在高能密度材料的合成[1-2]、炸药冲击起爆[3]及材料的动态特性分析[4]等研究领域有广泛的应用。因此,准确地获取研究所需的平面冲击波至关重要。
目前实验室常采用气体炮[5]驱动飞片撞击靶板产生所需的平面冲击波。冲击波压力峰值和峰值平台压力保持时间(脉冲宽度)是表征平面冲击波强度的两个重要特征指标。汤文辉等[6]基于流体动力学理论提出了靶板撞击面冲击波压力峰值和脉冲宽度的计算模型,在一定程度上为冲击波压力的获取提供了理论指导。但是,该模型是在一定的理想假设条件下根据飞片撞击靶板过程中起支配作用的物理定律而获得的,需要飞片或靶板材料在高压下的物态方程及相关物态参数(如冲击雨贡纽参数)的准确资料,才能对靶板撞击面的冲击波压力做出预估。然而,当飞片或靶板材料为冲击雨贡纽参数未知的材料,如99.99%(质量分数)纯镍、96%(质量分数)氧化铝时,将不能利用该模型预估靶板撞击面冲击波的压力峰值和脉冲宽度。目前在涉及到相关研究时,只能分别利用Ni200[7]和Al300[8]的冲击雨贡纽参数进行粗略的估算。此外,即使飞片和靶板材料的雨贡纽参数已知,不同批次的飞片或靶板的雨贡纽参数也有所差异。因此,有必要对飞片与靶板撞击面的压力峰值和脉冲宽度的理论模型做进一步研究。
本工作采用量纲分析法对影响靶板撞击面冲击波压力峰值和脉冲宽度的因素进行分析,以期获得靶板撞击面冲击波压力峰值和脉冲宽度的经验模型;并通过实例分析,检验该经验模型的可行性。
2 平面冲击波的经验模型
将圆柱形平头飞片撞击半无限厚靶板[9]的过程看作平面平行正碰撞,影响靶板撞击面冲击波压力峰值pm的因素有:飞片速度v,飞片和靶板的材料密度ρ01、ρ02,飞片和靶板的雨贡纽参数C01、S1和C02、S2;影响脉冲宽度τ的因素有:飞片速度v,飞片直径D及长度L,飞片和靶板的材料密度ρ01、ρ02,飞片和靶板的雨贡纽参数C01、S1和C02、S2,飞片材料的泊松比ν及Grüneisen系数γ1。由于γ1、S1、ν及S2为无量纲量,为便于研究,将它们合并为γ1/S1、S1/ν和S1/S2。pm和τ与上述影响因素之间存在如下函数关系
(1)
为简化量纲分析过程,将与两个因变量pm和τ相关联的各影响因素合并成一个函数关系式
(2)
在飞片撞击靶板的物理过程中,选择质量、长度和时间为基本量纲,分别记作M、L、T,由相似理论的Buckingham定理[10-11],物理方程可变换成无量纲组合量(π数)的关系方程式,且无量纲关系式中应当涉及9个(12-3=9)无量纲量。由于γ1/S1、S1/ν和S1/S2已是无量纲量,故只需用量纲分析方法再求取6个(9-3=6)无量纲参量即可。无量纲π项的一般指数形式为
(3)
式中:x1~x9分别表示各相应物理量的指数。写出各相应物理量的量纲,列于表1。
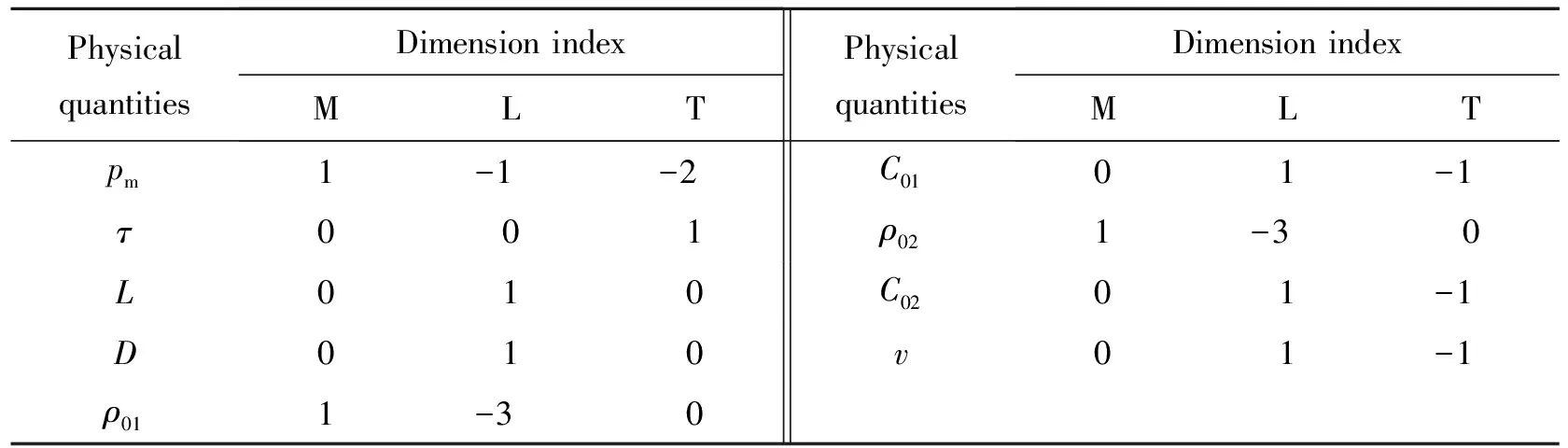
表1 相应物理量的量纲Table 1 Dimensions of the corresponding physical quantities
根据量纲的齐次性原则可得各指数的联立方程组
(4)
(4)式中有9个未知数,需指定6个才能得到一组解,即一个无量纲的组合量。用x4~x9表示x1~x3,有
(5)
若指定一组x4~x9,由(5)式求出相应的x1~x3,就可获得所需的6个物理量,如表2所示。根据表2有:π1=L/D,π2=L2ρ01/(pmτ2),π3=τC01/L,π4=L2ρ02/(pmτ2),π5=τC02/L,π6=τv/L。参考(1)式,将π1~π66个量做适当变换,得到6个物理意义较为明确的物理量,即pm/(ρ01C01v)、τv/L、L/D、ρ01/ρ02、C01/C02、v/C01。
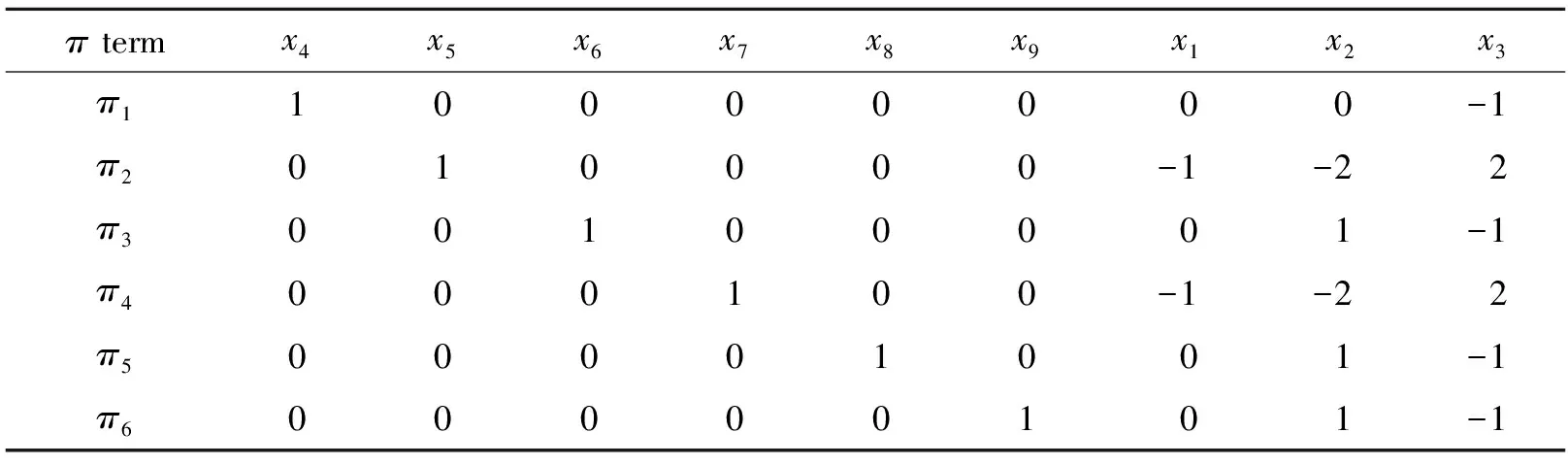
表2 相似比求解Table 2 Solution of similar ratio
综合考虑(1)式及另3个无量纲量γ1/S1、S1/ν和S1/S2,可得到靶板撞击面冲击波压力峰值和脉冲宽度的无量纲经验模型
(6)
式中:a1、b1、c1、d1、a2、b2、c2、d2、e2、f2、g2、h2均为常数。显然(6)式中各项都有明确的物理意义:ρ01/ρ02、C01/C02、γ1/S1、S1/S2及S1/ν反映了飞片和靶板的材料属性对压力峰值pm和脉冲宽度τ的影响,v/C01反映了飞片速度的影响,L/D反映了飞片结构尺寸对脉冲宽度τ的影响。
3 实 例
杨超等[12-13]基于∅100 mm一级轻气炮分别进行了3、4及5 mm厚飞片撞击靶板的加载实验,飞片材料是45钢,飞片直径为100 mm,靶板材料为纯镍(质量分数为99.99%)。在6种冲击实验条件下获得的飞片速度值、靶板撞击面冲击波压力峰值和脉冲宽度数据列于表3,将前4组实验数据用于建立经验模型,后两组则用于检验经验模型的可行性。
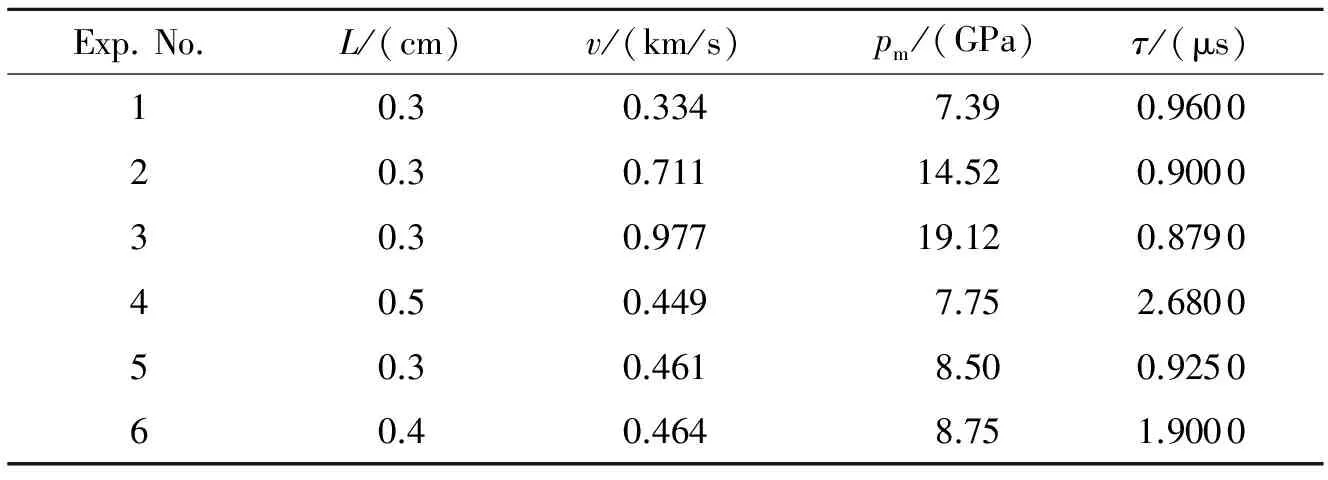
表3 实验数据Table 3 Experimental data
由于飞片和靶板的材料以及飞片的直径一定,(6)式中的D、ρ01、C01、ρ02、C02、γ1、S1、S2及ν都是常数,采用g-cm-μs单位制,则(6)式可简化为如下经验模型
(7)
式中:s1、s2、t1、t2及λ均为常数。
采用数据回归的方法对表3中前4组实验数据进行处理,可获得(7)式中s1、s2、t1、t2及λ的值,建立靶板撞击面冲击波压力峰值和脉冲宽度经验模型的定量关系,如下
(8)
用后两组实验数据对经验模型(8)式进行检验,结果如表4所列。根据经验模型(8)式计算得到的冲击波压力峰值的预测值与实验结果之间的相对误差小于9%,压力脉冲宽度的预测值与实验结果之间的相对误差小于12%。

表4 压力峰值和脉冲宽度的实测值与模型预测值的对比结果Table 4 Comparison of the measured values of peak pressure and pulse widthwith those predicted by this model
Note:pm,jandτjare the predicted values of peak pressure (pm) and pulse width (τ),respectively.
4 结 论
采用量纲分析法对影响压力峰值和脉冲宽度的因素进行分析,分别获得了靶板撞击面冲击波压力峰值和脉冲宽度的经验模型。通过实例分析,获得了45钢撞击纯镍产生的平面冲击波的经验模型定量关系式,并且经验模型的预测值与实验测量值较为吻合。该经验模型的提出,使直接开展冲击加载实验建立不同冲击条件下平面冲击波的预估模型成为可能。
[1] KIM M,YOO C S.Highly repulsive interaction in novel inclusion D2-N2compound at high pressure:Raman and X-ray evidence [J].J Chem Phys,2011,134(4):44-51.
[2] 罗 宁,胡 强,李尚升.人造金刚石的合成技术分析 [J].应用技术,2010(20):257.
LUO N,HU Q,LI S S.Analysis of artificial diamond synthesis technology [J].The Application of Technology,2010(20):257.
[3] PULHAM C R,MILLAR D I A,OSWALD I D H,et al.High-pressure studies of energetic materials [M]//Boldyreva E,Dera P.High-pressure crystallography.Netherlands:Springer Netherlands,2010:447-457.
[4] 曾代朋,陈 军,谭多望.超压爆轰产物冲击绝热线的实验研究 [J].高压物理学报,2010,24(1):76-80.
ZENG D P,CHEN J,TAN D W.Over pressure experimental study on detonation products shock Hugoniot [J].Chinese Journal of High Pressure Physics,2010,24(1):76-80.
[5] PAVLENKO A V,BALABIN S I,KOZELKOV O E,et al.A one-stage light-gas gun for studying dynamic properties of structural materials in a range up to 40 GPa [J].Instrum Exp Tech+,2013,4(56):482-484.
[6] 汤文辉,张若棋,陈雪芳.LY12-M铝中冲击波衰减机理的实验研究 [J].高压物理学报,1988,2(3):218-226.
TANG W H,ZHANG R Q,CHEN X F.Experimental study on the mechanism of shock wave attenuation in LY12-M aluminum [J].Chinese Journal of High Pressure Physics,1988,2(3):218-226.
[7] CHAN K S,TIAN J W,YANG B,et al.Evolution of slip morphology and fatigue crack initiation in surface grains of Ni200 [J].Metall Mater Trans A,2009,40(11):2545-2556.
[8] 杜晓松,郝建德,杨邦朝,等.薄膜式锰铜传感器的超高压力标定 [J].仪器仪表学报,2001,22(增刊2):151-152.
DU X S,HAO J D,YANG B C,et al.Calibration of thin-film ultrahigh pressure manganin gauges[J].Chinese Journal of Scientific Instrument,2001,22(Suppl 2):151-152.
[9] 陈卫东,张 忠,刘家良.破片对屏蔽炸药冲击起爆的数值模拟和分析 [J].兵工学报,2009,30(9):1187-1190.
CHEN W D,ZHANG Z,LIU J L.Numerical simulation and analysis of fragments impact initiation of shielded explosive [J].Acta Armamentarii,2009,30(9):1187-1190.
[10] 谈庆明.量纲分析 [M].合肥:中国科学技术大学出版社,2007:100-110.
TAN Q M.Dimensional analysis [M].Hefei:University of Science and Technology of China Press,2007:97-98.
[11] KISELEV S P.Numerical simulation of wave formation in an oblique impact of plates by the method of molecular dynamics [J].Journal of Applied Mechanics and Technical Physics,2012,53(6):907-917.
[12] 杨 超,经福谦,张万甲.冲击波压力和脉冲持续时间对铁和镍微结构的影响 [J].兵器材料科学与工程,1996,19(3):38-44.
YANG C,JING F Q,ZHANG W J.Effects of shock pressure and pulse duration on micro structure of iron and nickel [J].Ordnance Material Science and Engineering,1996,19(3):38-44.
[13] 杨 超,经福谦,张万甲,等.冲击加载作用下铁和镍的高应变率变形 [J].兵器材料科学与工程,1996,19(1):49-54.
YANG C,JING F Q,ZHANG W J,et al.High strain rate deformation of Fe and Ni by shock loading [J].Ordnance Material Science and Engineering,1996,19(1):49-54.

