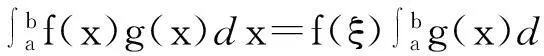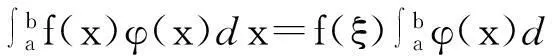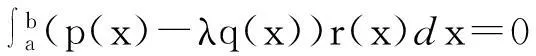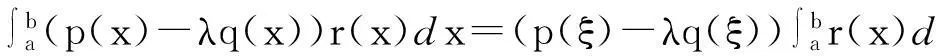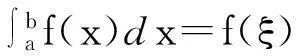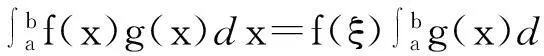积分型中值定理的推广及统一表示

陈　玉

(江西师范大学数学与信息科学学院，江西南昌330022)



积分型中值定理的推广及统一表示

陈玉

(江西师范大学数学与信息科学学院，江西南昌330022)

[摘要]通过减弱连续的条件，推广了一类积分型中值定理，在适当的条件下，用一个式子将Lagrange中值定理、Cauchy微分中值定理、积分型Cauchy中值定理、积分中值定理、积分第一中值定理、Lagrange型积分中值定理、Cauchy型积分中值定理及推广的积分第一中值定理这8个中值定理统一起来.

[关键词]积分中值定理； 微分中值定理； 原函数

1引言

积分中值定理在微积分理论中占有十分重要的地位.近年来，人们利用微分中值定理证明积分中值定理，对积分中值定理与微分中值定理的内在联系及形式上的统一进行了不少研究，如文献[1-7].其中，文献[5]探讨了积分型中值定理的统一表示的问题，利用Rolle定理推广了文献[8-9]中的积分型Cauchy中值定理的形式，在适当的条件下，将Lagrange中值定理、Cauchy微分中值定理、积分型Cauchy中值定理、积分中值定理和积分第一中值定理用一个式子统一表示出来，得到了一类连续函数的积分型中值定理；文献[6]将连续的条件减弱，利用微分中值定理得到了Lagrange型积分中值定理，Cauchy型积分中值定理，分别推广了积分中值定理与文献[8-9]中的积分型Cauchy中值定理；文献[7]利用Cauchy中值定理，通过减弱被积函数乘积因子连续的条件，推广了积分第一中值定理，得到了文献[5]推论4的推广形式.

本文将进一步研究积分中值定理与微分中值定理形式上的统一问题.通过减弱文献[5]中连续的条件，进一步推广积分型中值定理，在适当的条件下，不但将Lagrange中值定理、Cauchy微分中值定理、积分型Cauchy中值定理、积分中值定理、积分第一中值定理，而且将Lagrange型积分中值定理、Cauchy型积分中值定理及推广的积分第一中值定理这8个中值定理用一个式子统一表示，进一步揭示了积分中值定理与微分中值定理之间的内在联系，有助于人们深入地理解这些中值定理间的关系，所得结果推广了文献[5-8]的结果.

为后面讨论的方便，先将有关定理叙述如下.

定理1[5]设p(x)，q(x)，r(x)在[a，b]上连续，∀x∈[a，b]，q(x)，r(x)≠0，则存在ξ∈(a，b)，使得

(1)

推论1[5]在(1)式中，当p(x)=f′(x)， q(x)， r(x)=1时，∃ξ∈(a，b)，使得

f(b)-f(a)=f′(ξ)(b-a).

这就是Lagrange微分中值定理形式，这里要求f′(x)在[a，b]上连续，条件太强了，有待于改进.

推论2[5]在(1)式中，当p(x)=f′(x)， q(x)=g′(x)， r(x)=1时，∃ξ∈(a，b)，使得

这就是Cauchy微分中值定理形式，这里要求f′(x)，g′(x)在[a，b]上连续，条件较强.

如果取p(x)=f(x)， q(x)=g(x)， r(x)=1，则(1)式为

这就是文献[9]提到的积分型Cauchy微分中值定理.

推论3[5]在(1)式中，当p(x)=f(x)， q(x)=r(x)=1时，∃ξ∈(a，b)，使得

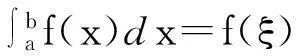
这就是积分中值定理.

推论4[5]在(1)式中，当p(x)=f(x)， q(x)=1， r(x)=g(x)时，∃ξ∈(a，b)，使得

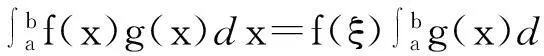
这就是积分第一中值定理.这里要求g(x)≠0，比要求函数g(x)不变号的条件要强些.

定理2[6](Lagrange型积分中值定理)设f(x)在[a，b]上可积，且在[a，b]上有原函数，则存在ξ∈(a，b)，使得

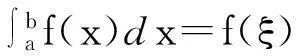
定理3[6](Cauchy型积分中值定理)设f(x)，g(x)在[a，b]上可积，且在[a，b]上有原函数，g(x)≠0(a

定理4[7]设f(x)在[a，b]上连续，g(x)在[a，b]上可积且有原函数，g(x)≠0(a

2主要结论

下面给出本文的主要结论.

定理5设p(x)，q(x)，r(x)在[a，b]上可积，且在[a，b]上有原函数，q(x)，r(x)≠0(a

由于可积但不连续的函数也可以有原函数[1]，而连续函数必可积且有原函数，因此定理5的条件比定理1更弱，定理1成为定理5的一个推论，从而进一步推广了积分型中值定理.

定理5的证明需要以下引理.

引理2[11]设f(x)，g(x)均为定义在[a，b]上的有界函数，若仅在[a，b]中有限个点处f(x)≠g(x)，则当f(x)在[a，b]上可积时，g(x)在[a，b]上也可积，且

证设

由f(x)在[a，b]上可积知，f(x)在[a，b]上有界.即存在M>0，对所有x∈[a，b]，有|f(x)|≤M，从而|f(x)|≤M，(x∈(a，b))，则

即F(x)在[a，b]上有界.由引理2得，F(x)在[a，b]上可积，且

又F(x)>0，x∈[a，b]，由引理1，有

从而

引理4[12]若f(x)在闭区间[a，b]上可积，且在[a，b]上有原函数， φ(x)在[a，b]上可积且不变号，则在(a，b)内至少存在一点ξ，使得

下面给出定理5的证明.

证设r(x)在[a，b]上的原函数为R(x)，R′(x)=r(x).由条件r(x)≠0(a

否则，若∃x1，x2∈[a，b]，x1≠x2，使得

r(x1)r(x2)<0，

即

R′(x1)R′(x2)<0，

不妨设x1

由引理4知，∃ξ0∈(a，b)使得

又q(x)≠0(a

(2)

易知，p(x)-λq(x)在[a，b]上可积且在[a，b]上存在原函数，由引理4知，∃ξ∈(a，b)使得

p(ξ)-λq(ξ)=0，

而q(x)≠0(a

即

推论5在定理5中，当p(x)=f′(x)，q(x)，r(x)=1时，∃ξ∈(a，b)，使得

f(b)-f(a)=f′(ξ)(b-a).

这就是Lagrange微分中值定理形式，这里将推论1f′(x)在[a，b]上连续的条件减弱为f′(x)在[a，b]上可积，改进了推论1.

推论6在定理5中，当p(x)=f′(x)， q(x)=g′(x)， r(x)=1时，∃ξ∈(a，b)，使得

这就是Cauchy微分中值定理形式，这里只要求f′(x)，g′(x)在[a，b]上可积，改进了推论2.

推论7在定理5中，当p(x)=f(x)，q(x)=r(x)=1时，∃ξ∈(a，b)，使得

这就是定理2[6](Lagrange型积分中值定理)，是推论3积分中值定理的推广.

推论8在定理5中，当p(x)=f(x)， q(x)=g(x)， r(x)=1时，则∃ξ∈(a，b)，使得

这就是定理3[6](Cauchy型积分中值定理)，是文献[8-9]积分型Cauchy微分中值定理的推广.

在定理5中，令p(x)=f(x)， q(x)=1， r(x)=g(x)，即得

推论9设f(x)，g(x)在[a，b]上可积，且在[a，b]上有原函数，g(x)≠0(a

推论9进一步推广了积分第一中值定理，减弱了定理4[7]中f(x)在[a，b]上连续的条件，改进了定理4.

定义如果对任意的x∈[a，b]，f(x)>0或对任意的x∈[a，b]，f(x)<0，称函数f(x)在[a，b]上严格不变号.

从定理5的证明过程中可以看出以下结论成立：

推论10设f(x)在[a，b]上有原函数，且f(x)≠0(a

在推论9中，g(x)≠0(a

通过以上推论5-9以及它们与推论1-4的关系，我们看到，通过加强函数的某些条件，可以把微积分学中主要的中值定理及其推广形式统一在定理5的一个式子中，这也揭示了它们之间的内在联系.

[参考文献]

[1]周民强.数学分析(第二册)[M].上海：上海科学技术出版社，2003：24-59，328.

[2]陈大均.微积分基本公式和中值定理[J].工科数学，1995，11(1)：171-172.

[3]郑权.基于微分中值定理证明微积分基本公式和积分中值定理[J].大学数学，2003，19(6):121-122.

[4]丁殿坤，邹玉梅.微分中值定理和Newton-Leibniz公式可互相证明[J].大学数学，2005，21(4)：128-129.

[5]伍建华，孙霞林，熊德之.一类积分型中值定理的渐近性讨论[J].西南师范大学学报(自然科学版)2012，37(8):24-27.

[6]陈玉.基于微分中值定理的积分中值定理[J].高等数学研究，2013，16(6):42-45.

[7]陈玉.积分第一中值定理的推广[J].江西科学，2014，32(2):178-180.

[8]严振祥.定积分中值定理的推广[J].上海海运学院学报，1995，16(1):29-33.

[9]戴立辉，刘龙章.积分型Cauchy中值定理中间点的渐近性[J].大学数学，2009，25(3):168-172.

[10]李衍禧.积分第一中值定理的推广[J].数学的实践与认识，2007，37(9):203-206.

[11]华东师范大学数学系.数学分析[M].4版.北京：高等教育出版社，2010:215.

[12]关若峰.积分中值定理的推广[J].广州大学学报，2004，3(6):499-500.

Extension and Unified Representation of

Integral Mean Value Theorems

CHENYu

(Department of Mathematics and Informatics， Jiangxi Normal University，Nanchang 330022，China)

Abstract:This paper generalizes a class of integral mean value theorems by weakening the condition of continuity. When appropriate conditions are satisfied， this paper unifies Lagrange and Cauchy mean value theorems of differential， Cauchy mean value theorem of integral type， mean value theorem for integrals and its extension， the first mean value theorem for integrals and its extension， mean value theorem for integrals of Lagrange and Cauchy type by one equality.

Key words:mean value theorem for integrals; mean value theorems of differential; original function

[基金项目]国家自然科学基金(11201195)； 江西师范大学校级教改课题

[收稿日期]2014-10-20

[中图分类号]O172.2

[文献标识码]C

[文章编号]1672-1454(2015)02-0061-05