原函数存在性及变上限定积分的可导性研究

王志武,王希超

原函数存在性及变上限定积分的可导性研究

王志武,王希超

山东农业大学信息科学与工程学院, 山东 泰安 271018

原函数和定积分是高等数学中的重要概念和基本内容。本文以闭区间上的函数为例，着重探讨了函数在存在有限个第一或第二类间断点的情况下，原函数的存在性，以及变上限定积分的存在性，此时原函数与函数的变上限定积分的关系。

原函数; 变上限定积分; 间断点; 连续; 可积

1 函数原函数的存在性

定理2若函数()在闭区间[,]上有定义,且只存在有限个第一类间断点或无穷间断点,则()在[,]上不存在原函数.

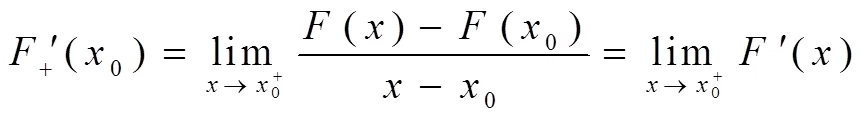
（1）当0为()的可去间断点时,(- 0)=(+ 0)≠(0);

（2）当0为()的跳跃间断点时,(- 0)≠(+ 0);

（3）当0为()的无穷间断点时,(- 0)与(+ 0)至少有一个为无穷.

以上均与ʹ(0)=(0)矛盾，所以函数()不存在原函数.

当()在闭区间上只有有限个振荡间断点时,()的原函数可能存在也可能不存在.

本实验利用EXCEL 2010统计分析软件进行数据整理，利用Origin 9.0作图，利用IBM SPSS Statistics 22软件对数据进行差异显著性检验（p＜0.05为差异显著；p＜0.01为差异极显著）。

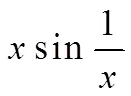
2 变上限定积分的存在性及其可导性

定义设函数()在闭区间[,]上可积,称∫(),Î[,]为变上限定积分.

定理4若函数()在闭区间[,]上有定义,且只存在有限个可去间断点,则变上限定积分∫()在[,]上存在且可导.

证明首先()在闭区间[,]上只有有限个可去间断点,从而∫()存在.

其次,重新定义()闭区间[,]上可去间断点的函数值,使得()在[,]上连续.因为只是改变了有限个点的函数值,从而积分∫()不变,所以∫()在闭区间[,]上可导.

这里说明的是∫()的导数并不是函数(),因为()在[,]上没有原函数.

定理5若函数()在闭区间[,]上有定义,且只存在有限个跳跃间断点,则变上限定积分∫()在[,]上存在,但在间断点处不可导.

证明函数()在闭区间[,]上只存在有限个跳跃间断点,显然∫()在[,]上存在.

设0Î(,)为()的一个跳跃间断点,则(- 0)及(+ 0)存在,但:(- 0)≠(+ 0).

记()=∫(),Î[,],则()在0点的去心邻域内可导,由于:

不相等,所以()在0点不可导.

当函数()在闭区间[,]上只存在有限个无穷间断点时,变上限定积分∫()在[,]上可能存在,也可能不存在,存在时在()的间断点处不可导.

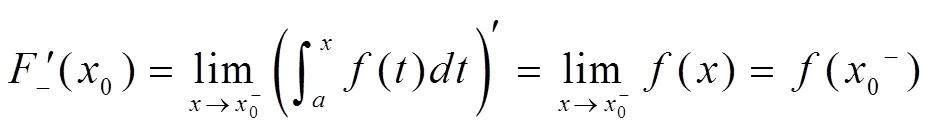
至少有一个为无穷,所以()在0点不可导.

当函数()在闭区间[,]上只有有限个振荡间断点时,变上限定积分∫()在[,]上可能存在,也可能不存在,存在时间断点处可能可导,也可能不可导.

[1] 华东师范大学数学系.数学分析(上册)[M].3版.北京:高等教育出版社,2003:209

[2] 同济大学数学教研室.高等数学(上册)[M].6版.北京:高等教育出版社,2007:227

[3] 王志武.泰勒公式中中值位置的研究[J].山东农业大学学报:自然科学版,2016,47(1):155-156

[4] 王志武,王希超.谈泰勒公式的教学[J].高等数学研究,2014,17(5):40-42

Study on the Existence of Primitive Function and the Derivability of Variable Upper Limit Integration

WANG Zhi-wu, WANG Xi-chao

271018,

Primitive function and definite integral are important concepts and basic contents in advanced mathematics. Taking a function on a closed interval as an example, this paper focuses on the existence of the primitive function and the variable upper limit integration, and the relationship between the primitive function and the variable upper limit integration of the function, in the case of a finite number of first or second class discontinuity points.

Primitive function; variable upper limit integration; discontinuity point; continuity; integrability

O151.2

A

1000-2324(2019)05-0918-03

10.3969/j.issn.1000-2324.2019.05.040

2017-02-13

2018-01-23

王志武(1963-),男,副教授,主要从事基础数学研究. E-mail:wangzw@sdau.edu.cn