基于PCA-NARX神经网络的溶解氧预测

袁红春,黄俊豪,赵彦涛

基于PCA-NARX神经网络的溶解氧预测

袁红春,黄俊豪*,赵彦涛

上海海洋大学 信息学院, 上海 201306

溶解氧是水产养殖中的一项重要水质参数，为了准确掌握溶解氧的变化趋势，提出了基于PCA-NARX神经网络的溶解氧预测模型。通过主成分分析法提取的主成分变量作为网络输入，优化了网络结构，并根据渔业养殖用水溶解氧标准，进行了NAR、NARX模型对溶解氧的短期（64 h）预测实验对比，仿真结果表明：PCA-NARX模型在16 h内均方根误差（RMSE）最小；32、48 h内，NAR模型与PCA-NARX模型预测精度基本一致；总体64 h之内，PCA-NARX模型相对于NAR、NARX模型具有更好的泛化能力，对溶解氧的预测性能较好。

溶解氧预测; NARX神经网络; 主成分分析

溶解氧(Dissolved oxygen，DO)在水体中的含量能够反映出水体的污染程度、生物的生长状况，是衡量水质优劣的重要指标之一[1]，国内外相关文献表明溶解氧的含量受到多种因素的影响，如水温、pH值、生物种类等，同时直接或者间接影响着养殖生物的生长[2,3]，相关渔业水质标准[4]也对渔业养殖用水的溶解氧在24 h中，16 h以上水溶解氧含量必须大于5 mg/L，任何时候不得低于3 mg的规定。因此，在水产养殖过程中监测水溶解氧的含量，预测其变化趋势对水产养殖有重要意义[5,6]。

近年来对溶解氧的预测方法主要有时间序列预测、支持向量机、组合预测、人工神经网络等，典型的有：孙国红等[7]采用时间序列预测方法对不同的水环境中溶解氧含量进行预测，由于在不同的水环境中，溶解氧的变化受到多种因素影响，时间序列模型只考虑了预测变量与自身历史变化之间的关系，缺乏对相关影响因子的考虑，从而准确性较差；刘双印等[8]采用支持向量机预测方法，构建了基于LSSVR的溶解氧在线预测模型，但是存在着算法复杂程度高、最佳训练参数的确定困难，易陷入局部最优解的问题[9,10]；吴慧英等[11]采用组合预测模型对溶解氧进行预测，实质上为两种常规预测模型的组合改进，缺点是执行过程较为复杂；由于神经网络具有自学习、自组织，并行处理信息和处理非线性信息的能力，能够挖掘数据背后的很难用数学式描述的非线性特征，弥补了传统时间序列模型的不足，从而被广泛应用于溶解氧预测问题[12,13]。

NARX（Nonlinear auto regressive models with exogenous inputs）即非线性有源自回归模型，是一种应用广泛的动态神经网络模型，Cadenas等[14]应用NARX模型对风速变化进行短期预测，Guzman等[15]运用NARX模型对密西西比地区地下水位进行长时间时间序列预测，蔡磊[16]等应用NARX模型对磁暴时SYM-H指数进行预测，并取得了不错的效果。本文采用基于主成分分析法（PCA）优化网络输入变量的NARX神经网络预测模型，即PCA-NARX神经网络模型，并结合相关专家经验与国家养殖用水标准，对溶解氧在短期（64 h内）含量变化进行时间序列预测。

1 模型构建

1.1 基本NARX网络模型

NARX网络被称为有外部输入的非线性自回归模型，属于动态递归神经网络，相当于具有输入延时的BP网络加上输出到输入的延时反馈连接[16]，NARX网络主要由输入层、隐层、输出层及输出到输入的延时构成，其网络结构如图1所示，由于输出层不断将包含历史的输出数据反馈到输入层，从而使NARX网络具有记忆能力，相比于传统回归神经网络包含更长时间的网络历史状态和实时状态信息。

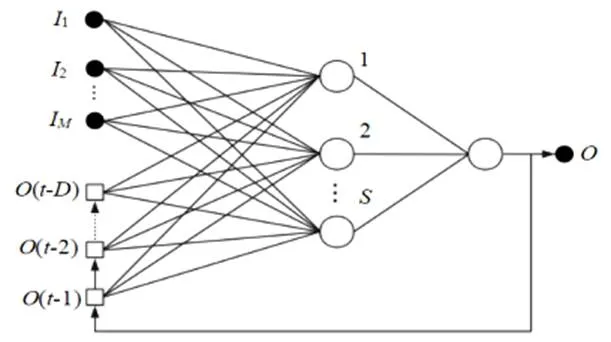
图1 NARX网络模型

假设()、()分别为网络在时刻的外部输入和输出，为输入数据的个数，为反馈时延的阶数，则对于网络时刻的输入()={1,2,...,I}，对应的反馈输入为()={(1),(2),...,()}，隐层第个神经元的输出

式中为隐层节点的激励函数，I为第个输入的值，w是个输入与第个隐含层神经元之间的连接权值，b是第个隐层神经元的阈值。网络的输出为

式中为隐层神经元的个数，w为第个隐含神经元与输出神经元之间的连接权值,b为输出神经元的阈值。

1.2 PCA-NARX溶解氧预测模型

1.2.1 输入变量的选择主成分分析法（Principal Components Analysis, PCA）是一种数据压缩和特征提取的多变量统计分析技术，本模型使用PCA对网络的外部输入变量进行降维，通过构造变量的一系列线性组合形成新变量，新的变量比原始数据维度更低，而且在彼此不相关的前提下反映原始数据的信息。通过PCA选择的主成分变量作为NARX网络的输入，既减少了输入变量的维数，又消除了由于输入变量的相关性不同对网络输出结果造成的影响，从而简化了网络的结构，提高了网络收敛性和稳定性。PCA主要过程如下

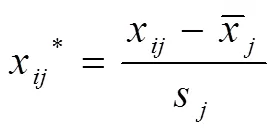
2) 根据公式（4）建立相关系数矩阵R×m。

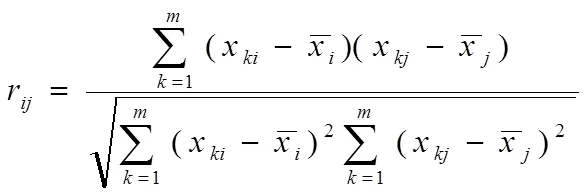
3) 求相关系数矩阵的特征根1≥2≥≥、特征向量1,2,…,u，并计算贡献率、累计贡献率。

主成分F的贡献率e为：

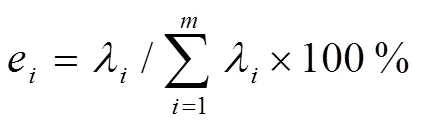
累计贡献率为：

本文选取累计贡献率90%以上的主成分变量为网络的输入，从而将网络输入维数由降为。

4）获得主成分矩阵。个样本对应个主成分变量构成的矩阵为：

5）A×p=Z×mU×p(7)

式中U×p为[1,2,…,u]。

1.2.2 性能评价指标预测模型性能评价是判断模型预测性能的关键，评价NARX模型性能的主要指标有均方根误差（）、相关系数（）、误差自相关系数（），用于判定预测值与实际输出值之间的偏差；用于判定两者的相关性，用于判定预测值与误差之间的相关程度，三者计算公式分别为：

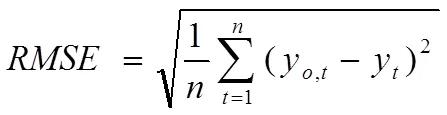
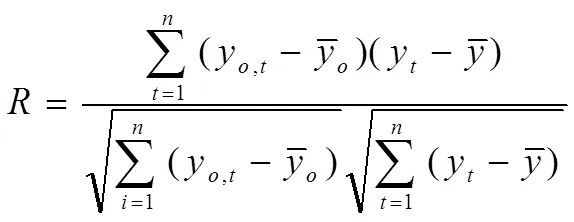
1.2.3 训练过程

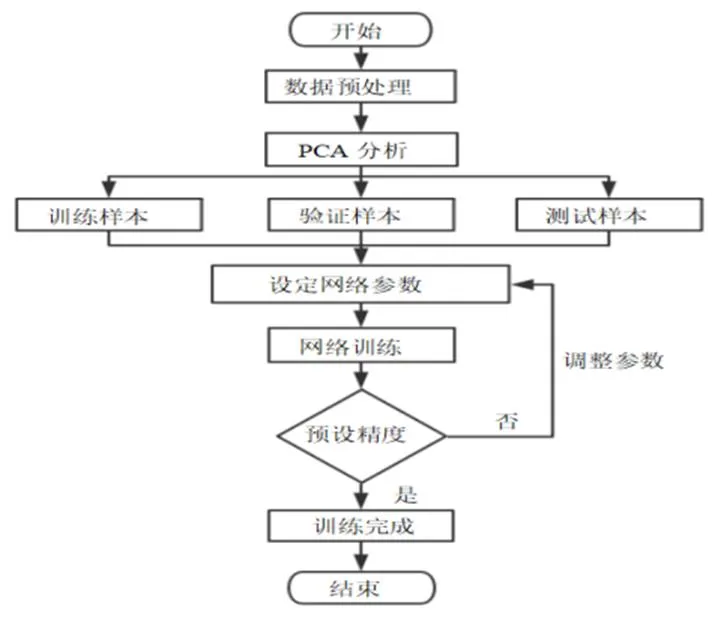
图2 PCA-NARX神经网络流程

图2是本文用于溶解氧预测的PCA-NARX 神经网络流程图。原始样本包括预测目标溶解氧数据、相关因子数据（本文所涉及的水温、酸碱度、氧化还原电位、盐度，浊度和海水比重共6项参数）。首先将原始样本数据进行预处理工作，包括数据归一化、异常数据处理；相关因子数据经过PCA分析后，剔除非主成分变量。将得到的主成分变量与预测变量合并为样本数据集，将样本数据集分为训练集、验证集，测试集三部分用于网络训练；训练过程采L-M（Levenberg-Marquardt）算法，该算法是使用最为广泛的非线性最小二乘算法，在中小规模的神经网络中，训练速度较快。网络训练过程中，每一次网络训练结束之后比较、与的值，训练初期，数值波动较为剧烈，后期趋于平稳，整体值逐渐增加，逐渐减小，在训练过程中反复调整隐层单元个数和延迟阶数，假设min()为训练中第次循环前最小，定义的训练终止的判断函数如下：

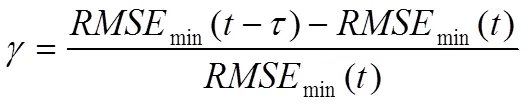
当<0.001时，认为网络的收敛已经接近极限，训练可以终止。训练结束之后，使用测试样本检验网络的性能。

2 数据处理及网络参数确定

2.1 数据来源

本文用于预测溶解氧的数据来源于课题组位于上海海洋大学校内养殖基地池塘2016年4月5日~25日的水质监测数据，由AP-2000型多参数水质仪探测到的水温（TEMP）、酸碱度（pH）、氧化还原电位（ORP）、溶解氧（DO）、盐度（SAL）、浊度（TDS）和海水比重（SSG）共7项参数。每三分钟获取一组数据，共9600组。根据长时间监测数据表明，每小时内各项参数指标浮动范围很小[12]，因此可以小时为单位，计算每小时各项参数的平均值，得到共计480组数据（表1）。

表1 样本数据

2.2 异常数据处理

2.2.1 缺失数据的处理对前后时间间隔不大的缺失水质数据，可以采用如（12）式线性插值法对其进行修复处理。

式中X和X+1分别为时刻和时刻水质参数，X为时刻水质的参数。对于缺失时间跨度较大的数据，可以采用天气类型相同或者相近的临近日期时间刻度相同的数据进行补全处理。

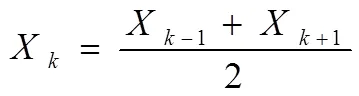
2.3 外部输入参数的确定

根据1.2.1描述的PCA提取主成分的方法，对除溶解氧之外的6项参数进行PCA主成分提取，计算特征值与贡献率，结果见表2。

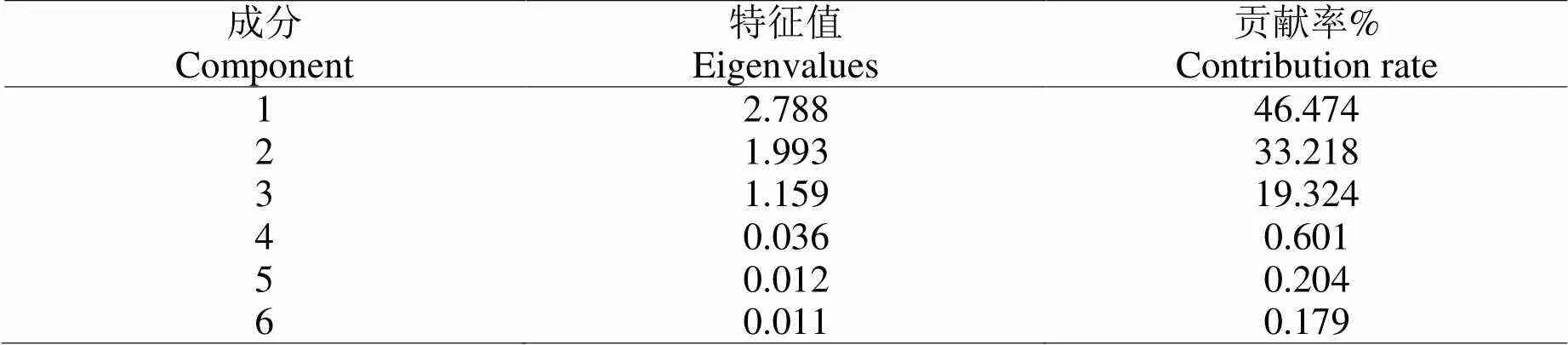
表2 成分分析

表3 主成分数据

经过PCA提取的前三个主成分贡献率分别为46.474%、33.218%和19.324%，图3展示了前三个成分的累积贡献率累计曲线，累计贡献率为99.016%，大于90%，说明三个主成分变量能够反映原始数据提供的绝大部分信息，因此主成分个数确定为3。根式(7)算出主成分矩阵，通过PCA分析将网络的输入由6维降低为3维，优化了网络的输入，得到的主成分变量1，2，3部分数据如表3。

2.4 网络结构的确定

将2.3章得到的主成分数据与原始的溶解氧数据合并，采用公式（14）进行归一化至[0.1,0.9]区间内，以消除不同量纲和数量级对网络训练的影响。

得到连续480 h（三个主成分变量和溶解氧）480组数据样本集，3项主成分为NARX网络的外部输入，下一时刻溶解氧的值为输出，取样本的70%为训练集，用于网络训练，15%为验证集，验证网络归一化程度，防止网络过拟合，15%为测试集，用于预测性能进行测试。用Matlab建立PCA-NARX网络，选择trainlm函数为训练函数，其中，反复调整隐层个数和延迟阶数，对比均方根误差、自相关系数和误差自相关系数，结果表明隐层个数为11延迟阶数为2的预测效果最佳。

3 仿真结果与分析

结合相关专家经验与渔业用水标准，为了验证PCA-NARX网络的预测效果，本文使用训练好的PCA-NARX溶解氧预测模型对2016年4月26日起连续64 h之内的水溶解氧含量进行预测，并与真实的数据进行对比，结果如图3所示。从图3可以看出，除溶解氧变化峰值与谷值处有略大误差，整体64 h内PCA-NARX神经网络模型得到的水溶解氧（DO）预测输出与实际值有较好的吻合。本文采用相同结构的NAR、NARX神经网络模型对溶解氧进行同时间段的预测性能比较，预测曲线如图4所示，三种网络预测模型均方根误差（RMSE）如表4所示。

图3 PCA-NARX神经网络64 h溶解氧预测

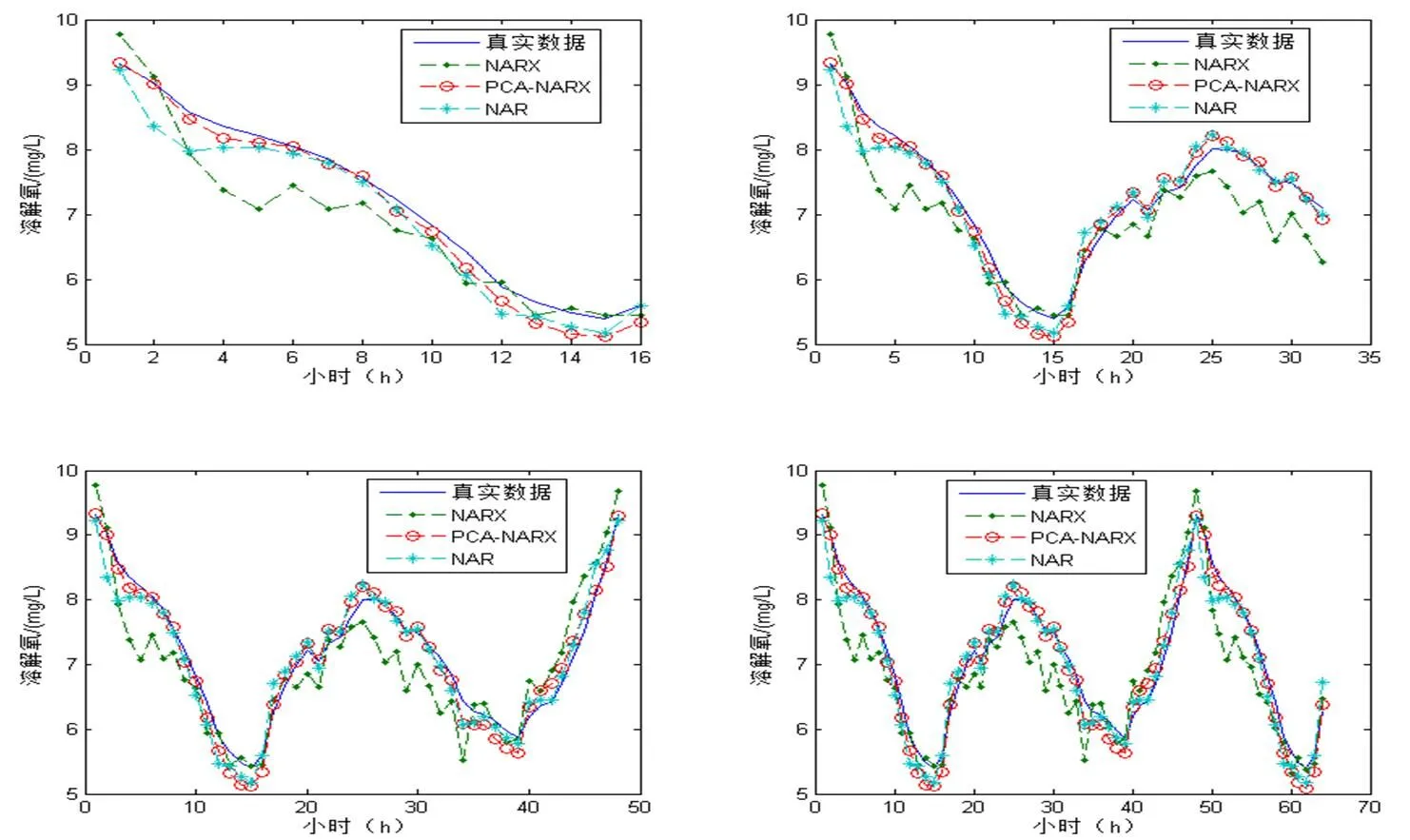
图4 NARX、PCA-NARX、NAR溶解氧预测

表4 RMSE统计

从图4三种网络预测曲线情况来看，NARX网络在1~10、25~35时段出现较大误差；NAR网络在溶解氧峰值、谷值处出现较大误差；整体上1~64 h内，PCA-NARX预测性能最优。从表4所示三种网络预测RMSE来看，PCA-NARX网络在1~16、1~48 h的RMSE均小于NAR与NARX网络，1~32 h略小于NAR模型，但总体64 h内，PCA-NARX网络对溶解氧的预测性能优于NARX、NAR神经网络模型，具有更高的预测精度、更优的泛化能力。

4 结论

本文采用PCA-NARX神经网络模型对水溶解氧进行时间序列预测，并与NAR、NARX网络模型在16、32、48、64 h内预测精度对比。结果表明，PCA-NARX模型在16 h内的均方根误差（RMSE）较NAR模型减少40.65%，较NARX模型减少55.37%；32、48 h内，NAR模型与PCA-NARX模型预测精度基本一致；总体上64 h之内的预测精度，PCA-NARX神经网络具有更小的均方根误差。PCA-NARX相对于传统NARX模型优化了网络输入变量，具有更优秀的泛化能力，同时又兼顾了NAR模型对预测周期性变化的优势，为水环境质量监测、渔业用水安全管理领域，提供了一个更高精度的水溶解氧预测模型。

[1] Segura-Noguera M, Cruzado A, Blasco D. The biogeochemistry of nutrients, dissolved oxygen and chlorophyll a in the Catalan Sea (NW Mediterranean Sea)[J]. Scientia Marina, 2016,80:39-56

[2] 黄岁樑,臧常娟,杜胜蓝,等.pH、溶解氧、叶绿素a之间相关性研究Ⅰ:养殖水体[J].环境工程学报,2011,5(6):1201-1208

[3] Lipizer M, Partescano E, Rabitti A,. Qualified temperature, salinity and dissolved oxygen climatologies in a changing Adriatic Sea[J]. Ocean Science, 2014,10(5):771-797

[4] 国家环境保护局.GB11607-1989.渔业水质标准[S].北京:中国标准出版社,1989

[5] 管崇武,刘晃,宋红桥,等.涌浪机在对虾养殖中的增氧作用[J].农业工程学报,2012,28(9):208-212

[6] Missaghi S, Hondzo M, Herb W. Prediction of lake water temperature, dissolved oxygen, and fish habitat under changing climate[J]. Climatic Change, 2017,141(4):747-757

[7] 孙国红,沈跃,徐应明,等.基于Box-Jenkins方法的黄河水质时间序列分析与预测[J].农业环境科学学报,2011,30(9):1888-1895

[8] 刘双印,徐龙琴,李道亮,等.基于时间相似数据的支持向量机水质溶解氧在线预测[J].农业工程学报,2014,30(3):155-162

[9] Tan GH, Yan JZ, Gao C,Prediction of water quality time series data based on least squares support vector machine[J]. Procedia Engineering, 2012,31:1194-1199

[10] Lü JK, Wang X, Zou W. A hybrid approach of support vector machine with differential evolution optimization for water quality prediction[J]. Journal of Convergence Information Technology, 2013,8(2):1158-1163

[11] 吴慧英,杨日剑,张颖,等.基于PCA-SVR的池塘DO预测模型[J].安徽大学学报(自然科学版),2016,40(6):103-108

[12] 袁红春,潘金晶.改进递归最小二乘RBF神经网络溶解氧预测[J].传感器与微系统,2016,35(10):20-23

[13] 宦娟,刘星桥.基于K-means聚类和ELM神经网络的养殖水质溶解氧预测[J].农业工程学报,2016,32(17):174-181

[14] Cadenas E, Rivera W, Campos-Amezcua R,. Wind speed forecasting using the NARX model, case: La Mata, Oaxaca, Mexico[J]. Neural Computing & Applications, 2016,27(8):2417-2428

[15] Guzman SM, Paz JO, Tagert MLM. The Use of NARX Neural Networks to Forecast Daily Groundwater Levels[J]. Water Resources Management, 2017,31(5):1591-1603

[16] 蔡磊,马淑英,蔡红涛,等.利用NARX神经网络由IMF与太阳风预测暴时SYM-H指数[J].中国科学(技术科 学),2010,40(1):77-84

Prediction of Dissolved Oxygen Based on PCA-NARX Neural Network

YUAN Hong-chun, HUANG Jun-hao*, ZHAO Yan-tao

201306,

Dissolved oxygen is an important aquatic parameter. In order to accurately grasp the trend of the dissolved oxygen accurately, the dissolved oxygen prediction model based on the PCA-NARX neural network is developed in this paper. The principal component variables extracted by principal components analysis (PCA) are used as exogenous inputs and the network structure was optimized，and short-term (64 h) prediction experiments of dissolved oxygen by NAR and NARX models were compared according to the standards of dissolved oxygen in fishery and aquaculture water. Simulation results show that the PCA-NARX model has a minimum root mean square error (RMSE) within 16 h，the prediction accuracy of the NAR model and the PCA-NARX model is basically the same within 32, 48 h. In addition, the comparisons with other models show that PCA-NARX neural network has better nonlinear fitting ability and superior in dissolved oxygen prediction based on the RMSE in short term (64 h). In total, within 64 h, PCA-NARX model has better generalization ability than the NAR and NARX model and better prediction performance for dissolved oxygen.

Prediction of dissolved oxygen; NARX neural network; principal component analysis

TP389.1

A

1000-2324(2019)05-0902-06

10.3969/j.issn.1000-2324.2019.05.037

2018-03-04

2018-04-28

国家自然科学基金(41776142);上海市科学技术委员会技术支撑(14391901400)

袁红春(1971-),男,博士,教授,主要从事专家系统、智能计算、智能信息处理等工作. E-mail:hcyuan@shou.edu.cn

Author for correspondence. E-mail:451222454@qq.com