从偏导数恒等式变换到偏微分方程求解

刘雄伟，王　晓

(国防科技大学理学院，湖南长沙410073)



从偏导数恒等式变换到偏微分方程求解

刘雄伟，王晓

(国防科技大学理学院，湖南长沙410073)

[摘要]从高等数学教材课后习题的偏导数恒等式变换求解，引导学生讨论一类偏微分方程的求解.在拓展课程内容、应用和常微分方程变量分离方法的基础上，巩固多元复合函数求导法则，常系数线性微分方程求解方法和傅里叶级数的相关理论与方法.

[关键词]高等数学； 偏导数； 偏微分方程； D’Alembert公式； 弦振动方程

在《高等数学》教材[1]多元微分学的课后习题中有这样一道练习：通过变换u=x-2y，v=x+3y将方程

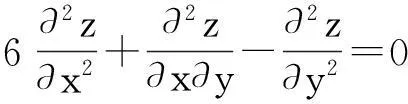
(1)

简化为

(2)

其求解过程是将函数z=z(x,y)看成是z=z(u,v)和两个中间函数u,v的复合函数，从而利用复合函数的求导法则，求z=z(x,y)关于x,y的二阶偏导数，并代入原式化简得到.

一般很多同学在做完这道练习以后，并没有对其内容与结论进一步思考和延伸.该问题是关于二元函数z=z(x,y)的偏导数恒等式，也就是偏微分方程.对于偏微分方程的代数解的获取一般是比较困难的.而这个问题的求解过程正好代表了一类偏微分方程的求解方法，即通过对(2)两端关于v求不定积分，有

(3)

对(3)式关于u求不定积分，得

(4)

其中F,G是两个包含任意常数的一元可微函数.

由于(2)中的z(u,v)的对应法则与(1)中的z(x,y)对应法则本质上讲是不同的，直观上记作z(x,y)=Z(u,v)=Z(x-2y,x+3y)更好理解，所以(2)-(4)中的z都应该记作Z.由(4)可得方程(1)的通解为

z(x,y)=Z(u,v)=Z(x-2y,x+3y)=F(x-2y)+G(x+3y).

(5)

如果将问题(1)加上两个初始条件，如

z|y=0=φ(x),zy|y=0=ψ(x)，

(6)

解由(1)和(6)构成的初值问题.

将(5)代入(6)中的两个初值条件，有

F(x)+G(x)=φ(x)，

(7)

-2F′(x)+3G′(x)=ψ(x).

(8)

对(8)两端在积分区间[x0,x]上求积分，有

(9)

联立(7)和(9)，可得

(10)

(11)

将(10)，(11)代入(5)，有

(12)

例如，可设(5)式中的φ(x)=5x2,ψ(x)=2x，则代入(12)，即得由(1)和(6)构成的初值问题的解为

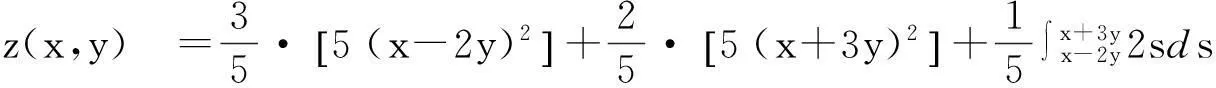
=5x2+2xy+31y2.

(13)

将(13)的结果代入(1)可知其满足等式，即为该偏微分方程满足初值条件(6)的解.

如果(1)中不包含混合偏导数，对应的参数y表示时间t，并记系数6为a2，则(1)和(6)构成的模型描述了物理上的无界弦自由振动问题[2]

(14)

对于该模型，可以使用特征线方法得到变量的变换公式，从而得到该问题上面描述类似的求解方法，也可以考虑分离变量与Fourier变换方法进行求解.它的解为

(15)

该公式称为弦振动方程初值问题(14)的达朗贝尔(D’Alembert)公式，使用该公式可以解决一类齐次线性常系数偏微分方程的定解问题.

进一步加上限制条件，可得如下有界弦自由振动的初边值问题[2]，即

(16)

若初始函数φ(x)和ψ(x)分别满足在闭区间[0,l]上三次连续可微和二次连续可微，且满足相容性条件

φ(0)=φ(l)=φ″(0)=φ″(l)=0，ψ(0)=ψ(l)=0，

则可以使用变量分离法，借助于常系数线性微分方程的求解方法以及对傅里叶级数展开的相关理论与方法，容易得其级数形式的解：

(17)

其中

(18)

(19)

定解问题(16)可以用来描述吉他、古筝等弦乐器上的一根弦的振动规律，u(x,t)表示t时刻x位置弦的横线位移.对任一时刻t0，有

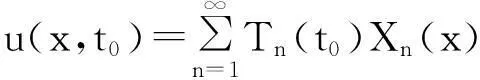
即在t0时刻弦的形状为正弦波，振幅随时间t0变化；对于任一位置x0，

为简谐振动的叠加，即弦在x0处做简谐振动，并且存在有振动过程中处于静止的节点和振幅达到最大的腹点，像这样具有不随时间t的变化而变化的节点和腹点的波即为物理上的驻波，即弦的振动是由无数驻波叠加而成的.在所有驻波的频率中，最小的频率为基频，基频发出的声音为决定声音音调的基音；其他的驻波频率是基频的整数倍，它们发出的声音为决定声音音色的泛音.

通过以上物理意义的分析，选取适当函数，从声学的角度对其描述的物理意义及决定声音要素的关系，借助于数学软件Mathematica的声音播放功能给予直观演示；并通过弦的不同位置与不同时刻的波形图形分析，进一步讨论弦振动振幅、频率对声音的影响.这样的处理，不仅可以达到拓宽学生知识面，激发应用数学知识分析、解决问题，诠释现象的兴趣，而且对深化所学知识的理解，培养正确的学习动机，促进学习效率的提高具有重要意义.

[参考文献]

[1] 朱健民，李建平. 高等数学(下册)[M]. 北京：高等教育出版社，2007: 142.

[2]张隽，沈守枫，潘祖梁. 数学物理方程与Mathematica软件应用[M]. 北京：机械工业出版社，2008: 36-42.

From the Partial Derivative Identity Transform to Solution of

Partial Differential Equations

LIUXiong-wei,WANGXiao

(College of Science, National University of Defense Technology, Changsha, Hunan 410073, China)

Abstract:The students were guided to discuss the solution of a class of partial differential equations by solving the problem of partial derivative identity transform from higher mathematics textbook. Based on developing course content, applications and the method of separation of variables for ordinary differential equations, it consolidated derivation rule of multiple compound function, methods of solving linear differential equations with constant coefficients and theories and methods of Fourier series.

Key words:higher mathematics； partial derivative； partial differential equations； D′Alembert figure； string vibration equation

[基金项目]湖南省普通高等学校教学改革研究立项项目(湘教通[2013]223号)；国防科技大学“十二五”本科教育教学研究立项课题(U2012105)

[收稿日期]2014-09-15；[修改日期]2015-01-05

[中图分类号]O13

[文献标识码]C

[文章编号]1672-1454(2015)02-0053-03