反三角函数的解析式及其应用

刘春平，　刘晓平

(1.扬州大学数学科学学院，江苏扬州225002；　2.扬州市职业大学数学学院，江苏扬州225002)



反三角函数的解析式及其应用

刘春平1，刘晓平2

(1.扬州大学数学科学学院，江苏扬州225002；2.扬州市职业大学数学学院，江苏扬州225002)

[摘要]从反函数的定义出发,给出了几个三角函数在定义域内某个单调区间上反函数的解析式,并应用它们对几道习题进行了解答.

[关键词]反函数； 反三角函数； 解析式

数学分析教材和习题集中，有一些涉及到反三角函数的题目[1-3], 如

题1试问下列等式是否成立：

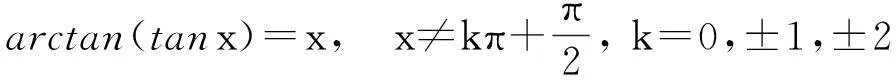
arcsin(sinx)=x,∀x∈.

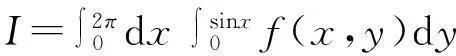
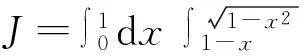
在教学过程中我们发现许多学生解答这些题目有一定的困难. 虽然文献[4]已明确指出：“所谓反三角函数只是三角函数在定义域内某个单调区间上的反函数，对一般三角函数而言，在定义域上并不存在反函数”. 文献[5]关于反正弦函数的主值arcsinx,反余弦函数的主值arccosx,以及反正切函数的主值arctanx等等也有详细的定义和讨论.但据我们所知，三角函数在定义域内某个单调区间上反函数的解析式却没有中学或大学教材给出过，因此学生不会利用解析式以及反三角函数的知识解答相关问题.

本文将从反函数的定义出发，首先给出如下三个函数:

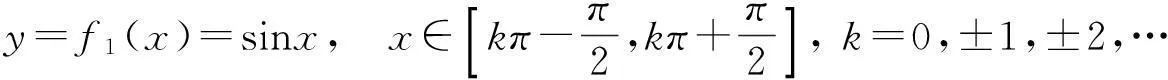
(1)

y=f2(x)=cosx,x∈[kπ,kπ+π],k=0,±1,±2,…,

(2)

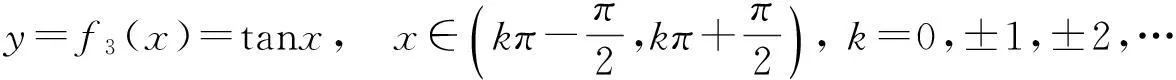
(3)

的反函数之解析式，然后解答题1—题3.

先回顾一下反函数的定义. 设函数

y=f(x),x∈D

(4)

满足：对于值域f(D)中的每一个值y,D中有且只有一个值x使得f(x)=y, 则按此对应法则得到一个定义在f(D)上的函数，称这个函数为函数f的反函数,记作

x=f-1(y),y∈f(D).

(5)

习惯上若用x作为自变量的记号，y作为因变量的记号，则函数(4)的反函数(5)可改写为

y=f-1(x),x∈f(D).

(6)

显然，函数f也是函数f-1的反函数,或者说f与f-1互为反函数,并有

f-1(f(x))≡x,x∈D,

(7)

f(f-1(x))≡x,x∈f(D).

(8)

sin(kπ+arcsinx)=xcoskπ=(-1)kx.

(9)

sin(kπ-arcsinx)=-xcoskπ=(-1)k+1x.

(10)

因此有

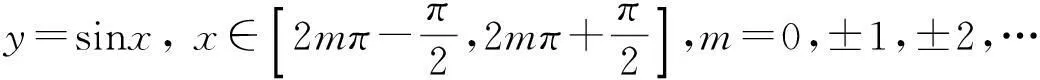
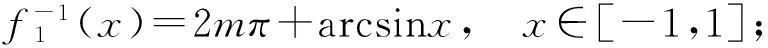
(11)

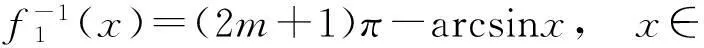
(12)

根据结论1，易得

推论1

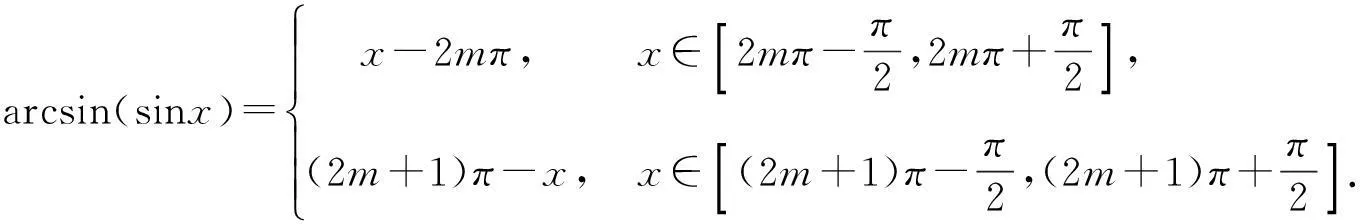
(13)

事实上，由f-1(f(x))≡x,x∈D, 有

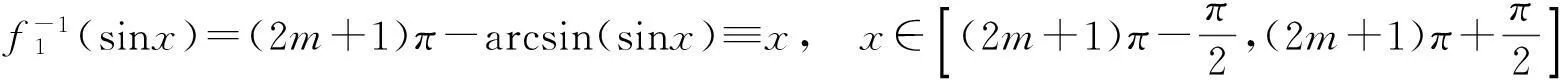
移项整理即得(13)式.

类似上述讨论过程，我们有

结论2函数y=cosx,x∈[2mπ,(2m+1)π],m=0,±1,±2,…的反函数为

(14)

函数y=cosx,x∈[(2m+1)π,(2m+2)π],m=0,±1,±2,…的反函数为

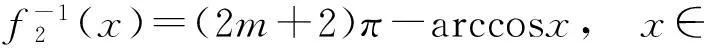
(15)

推论2

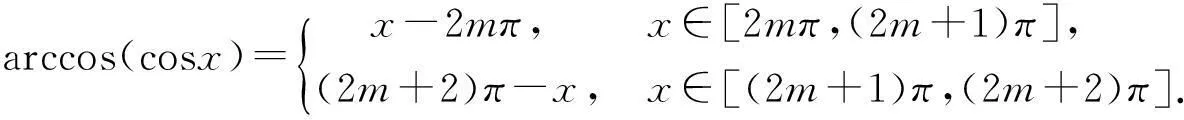
(16)

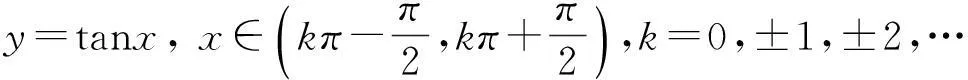
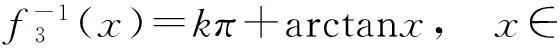
(17)

推论3

(18)

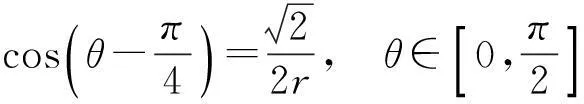
(19)

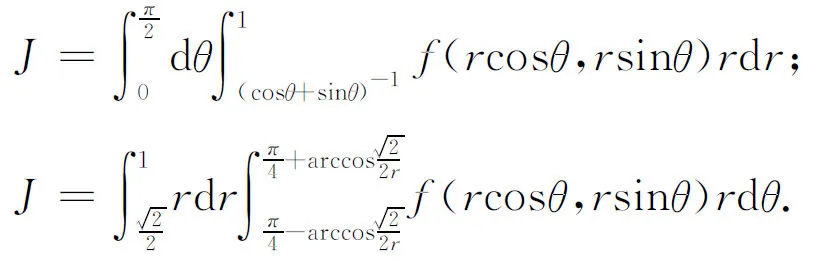
[参考文献]

[1]华东师范大学数学系.数学分析(上册) [M]. 3版.北京:高等教育出版社，2001:16.

[2]孙清华，孙昊. 数学分析疑难分析与解题方法(上册) [M].武汉: 华中科技大学出版社，2009:48.

[3]吉米多维奇. 数学分析习题集[M]. 北京:人民教育出版社，1978:386-387.

[4]周敏泽.中国华罗庚学校数学课本(高一年级)[M].吉林:吉林教育出版社，2002:132.

[5]菲赫金哥尔茨.微积分学教程(第一卷)[M]. 8版.北京:高等教育出版社，2006:87-91.

Analytic Expressions and Application of Some

Inverse Trigonometric Functions

LIUChun-ping1,LIUXiao-ping2

(1. Institute of Mathematics, Yangzhou University, Yangzhou 225002, China;

2.Institute of Mathematics, Yangzhou Polytechnic College, Yangzhou 225002, China)

Abstract:Starting from the definition of inverse function, this paper gives a few trigonometric functions within the domain on monotone interval analytic expressions of inverse function, and applies them to resolve a few exercises.

Key words:inverse function; inverse trigonometric function; analytic expressions

[收稿日期]2014-01-20

[中图分类号]O171

[文献标识码]C

[文章编号]1672-1454(2015)01-0088-03