空间解析几何中“向量代数”内容的处理方法

蒲和平，　于俊燕

(电子科技大学数学科学学院, 成都611731)



空间解析几何中“向量代数”内容的处理方法

蒲和平，于俊燕

(电子科技大学数学科学学院, 成都611731)

[摘要]讨论了空间解析几何中“向量代数”内容的处理方法，给出了从向量的代数形式到几何形式的具体处理方法，这种方法较传统方法更为简洁易懂，便于将二维与三维几何向量推广到n维向量,有利于大学数学与中学数学的衔接. 对大学数学教学与教材改革都具有积极的意义.

[关键词]空间解析几何； 向量代数； 几何形式； 代数形式

“空间解析几何”是大学理工类数学课程的基础. 在工科数学课程体系中“空间解析几何”没有作为一门独立的课程开设，而是作为章节的内容纳入了《高等数学》或《线性代数》的教材中，这种处理方式自然有其合理性，这里不作讨论. 本文主要针对“空间解析几何”中“向量代数”有关内容的处理方法作一些探讨.

在现行教材中“向量代数”内容的处理方法都大同小异，以同济大学《高等数学》教材为例, 按排了两节内容：第一节向量及其线性运算，第二节数量积、向量积、混合积.

在第一节向量及其线性运算中，先讲向量的概念，即将向量定义为“既有大小又有方向的量”，向量用有向线段表示；向量的加法规定为三角形法则或平行四边形法则，数乘按平行伸缩法则进行. 然后再建立空间直角坐标系，从而得到向量的坐标形式a=(ax,ay,az)及线性运算法则，即

(1)

这种处理方法不妨称为从几何形式到代数形式的方法.

第二节向量的内积(数量积)与外积(向量积)也是如此.

先将向量a和b的内积定义为

(2)

向量a与b的外积a×b定义为一个向量，该向量的方向与a和b均垂直，且a,b,a×b遵循右手法则，该向量的大小为

(3)

然后由以上定义，导出向量内积与外积的坐标计算公式：

a·b=(ax,ay,az)·(bx,by,bz)=axbx+ayby+azbz,

(4)

(5)

便于叙述，将以上方法称为“几何—代数”形式.

经教学研究与教学实践，我们认为改变以上内容的处理顺序会更为科学合理，即先以定义的方式给出向量线性运算的代数形式(1)以及内积与外积的坐标形式(4)，(5)，再推出各类运算的几何意义与公式(2)，(3). 我们将这种处理方法叫“代数—几何”形式.

其理由有三点：

一是在中学数学教学中已经按“几何—代数”形式介绍了向量及其线性运算(有的学校将平面向量部分作为必修，空间向量部分作为选修)，学生对向量及其线性运算的代数形式已经了解，可以直接按“代数—几何”形式介绍，避免不必要的重复, 有利于大学数学与中学数学的衔接.

二是便于将二维与三维几何向量推广到n维向量，有利于将解析几何与线性代数有机结合，融为一体.

三是按“代数—几何”形式处理相关部分的内容更为简洁，学生更易于理解、掌握.

下面就“代数—几何”形式的具体实施作一简略的介绍.

我们对向量的概念保持线性代数中一贯的定义方式，即称有序数组为向量. 在平面或空间直角坐标系中建立了点与向量的一一对应关系后，向量的大小与方向就有了明确的意义与计算公式，向量在轴上的投影等概念也就很容易建立.

向量的线性运算仍按(1)式的形式定义，由此很容易得到线性运算的性质，再结合向量坐标的几何意义会很快得到线性运算的几何意义，同时向量在轴上的投影及相关性质也很容易得到.

以上方法较为简单，并且在一些教材中也可以看到其部分描述，这里不再作详细的讨论. 下面就向量的内积、外积的“代数—几何”处理方式作较详细的讨论，因为这种处理方法在现行教材中还未曾有见.

先讨论内积的情况. 可由(4)式来定义两向量的内积，再由此推出(2)式. 事实上，由(4)式容易验证内积符合以下运算规律：

(i) a·a=a2=‖a‖2;

(ii) a·b=b·a;

(iii) (λa)·b=a·(λb)=λ(a·b),λ∈;

(iv) (a+b)·c=a·c+b·c.

由余弦定理可知

所以

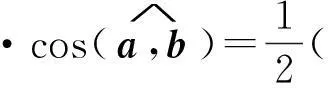
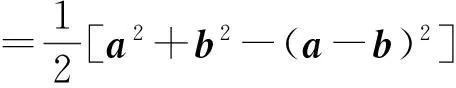
故(2)式成立.

再讨论外积的情况. 可由(5)式来定义两向量的外积，由此定义容易验证外积符合以下运算规律：

(i) a×a=0;

(ii) a×b=-b×a;

(iii) (λa)×b=a×(λb)=λ(a×b),λ∈;

(iv) (a+b)×c=a×c+b×c.

(iii)与(iv)利用向量的外积定义(5)式及行列式的性质是很显然的，但一般教材都没证明，因为按传统方式(即由(3)式给出的外积定义)证明十分麻烦.

由向量的外积定义(5)式容易得到(3)式所描述的两向量外积的几何意义. 事实上，由(5)式并利用内积的定义及行列式的性质，知

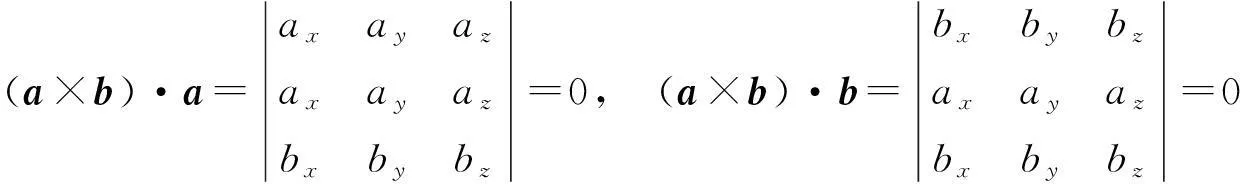
这说明向量的外积a×b与向量a和b均垂直.

再讨论向量的外积a×b的模.

‖a×b‖2=(aybz-azby)2+(azbx-axbz)2+(axby-aybx)2

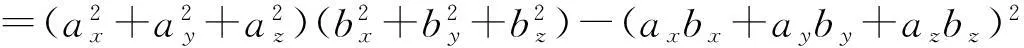
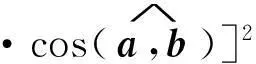
故(3)式成立.

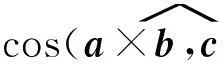
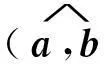
a=(1,0,0)，b=(cosθ,sinθ,0)，a×b=(0,0,sinθ).

这说明当θ>0时，a×b与z轴同向，否则与z轴反向，即a,b,a×b的方向遵循右手法则.

多年的教学实践告诉我们，用以上方式来处理“向量代数”的内容是行之有效的，较现行教材中的方法更为简便易懂，深受学生欢迎. 以此文交流，希望对我们的教学与教材改革有所帮助.

[参考文献]

[1]同济大学数学系.高等数学(下册)[M].6版. 北京：高等教育出版社，2007.

[2]上海交通大学数学系.大学数学：微积分(下册) [M]. 北京：高等教育出版社，2008.

[3]黄廷祝,成孝予. 线性代数与空间解析几何 [M].3版. 北京：高等教育出版社，2008.

[4]魏战线,李继成. 线性代数与解析几何[M].2版. 北京：高等教育出版社，2010.

The Processing Methods of ‘Vector Algebra’Content

in the Space Analytic Geometry

PUHe-ping，YUJun-yan

(School of Mathematics Sciences, University of Electronic Science and Technology of China, Chengdu 611731，China)

Abstract:This paper discusses the processing methods of "vector algebra" content in the space analytic geometry, gives the concrete treatment method of vector algebra form to geometry form. This method compared with the traditional method is more simple and easy to understand, easy to generalize two-dimensional and three-dimensional geometric vector ton-dimension vector. It is of benefit to link up the university mathematics and school mathematics, has positive significance to the university mathematical teaching reform and teaching material reform.

Key words:space analytic geometry； vector algebra； geometry form； algebra form

[收稿日期]2014-09-15

[中图分类号]G424

[文献标识码]C

[文章编号]1672-1454(2015)01-0059-03