函数arcsinx的幂级数的收敛性讨论

王利梅，　彭一鸣，　王　昊

(对外经济贸易大学，北京100029)



函数arcsinx的幂级数的收敛性讨论

王利梅，彭一鸣，王昊

(对外经济贸易大学，北京100029)

[摘要]用拉贝判别法, 沃利斯公式, 以及初等方法三种不同的方法, 讨论了函数arcsinx的麦克劳林展开式在收敛端点的收敛性, 即一个特殊数项级数的收敛性, 并根据幂级数的连续性得到数项级数的和.

[关键词]幂级数收敛性； 拉贝判别法； 沃利斯公式

1引言

函数的麦克劳林级数收敛区间的讨论是数学分析中一类非常常见的问题. 本文主要讨论函数arcsinx的情形. 由于

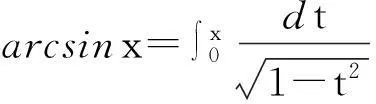
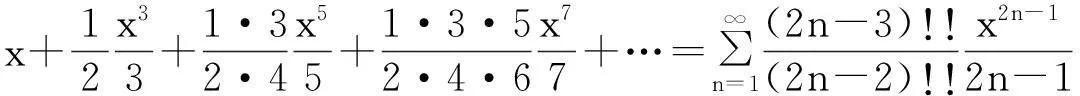
的收敛半径为R=1, 但此级数在收敛区间(-1,1)端点x=±1处的敛散性并不能由已知结论推出. 由于arcsinx为奇函数, 所以可以只讨论右端点x=1这种情况, 即讨论正项级数

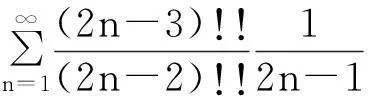
的敛散性.利用三种不同的方法证明了以下结论:

由前面的定理可立即得到下面的结论:

推论1

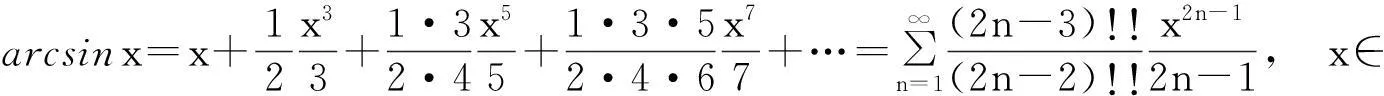
特殊地， 有

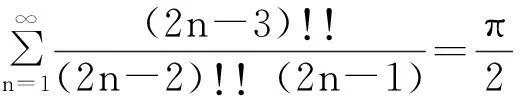
2预备知识

引理2(沃利斯(Wallis)公式)[1]

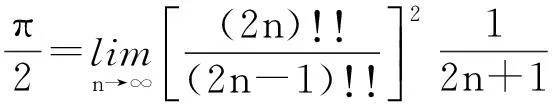
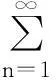
3定理的证明

为了证明的方便, 设

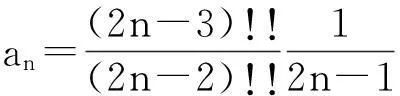
方法1(拉贝判别法)因为

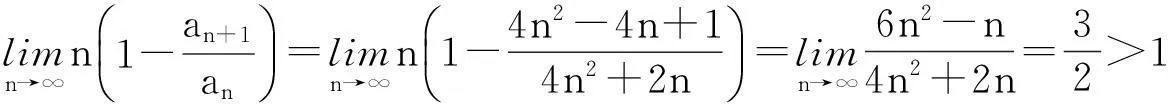
所以由拉贝判别法正项级数

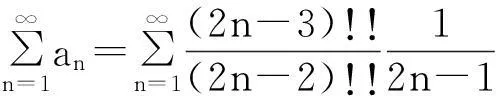
收敛.

方法2(沃利斯(Wallis)公式)由沃利斯(Wallis)公式

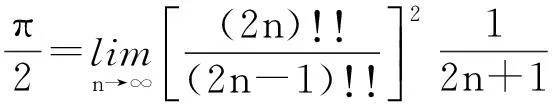
可得

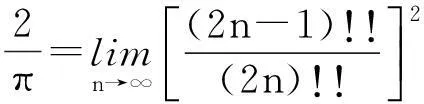
从而对任意的ε>0，存在N>0， 对于任意的n>N，成立

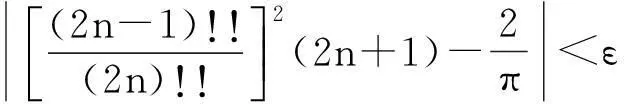
所以当n>N时， 有

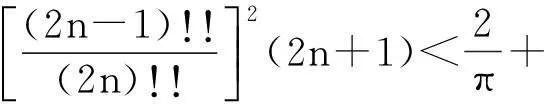
即有

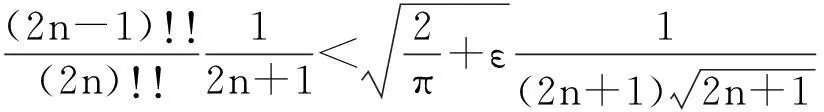
由ε的任意性， 不妨令ε=1，此时存在N>0， 对于任意的n>N，成立

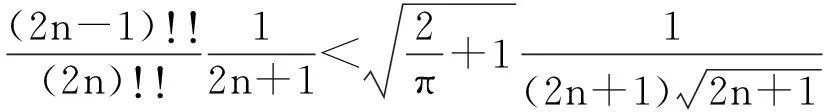
从而有

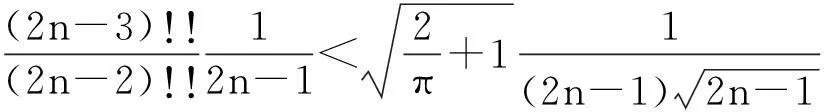
又由数项级数的积分判别法，易得

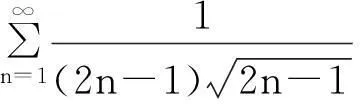
收敛，所以由维尔斯特拉斯判别法知数项级数

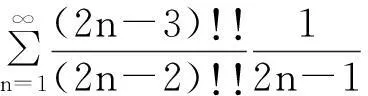
收敛.

方法3(初等方法)当n>1时，有

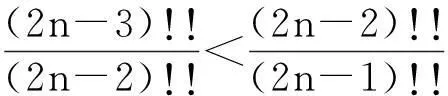
从而得

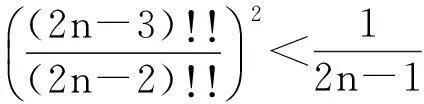
所以

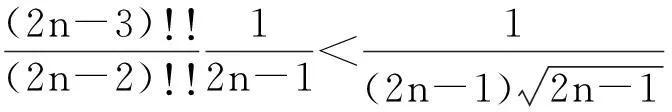
由引理3以及定理1 可得推论1.

[参考文献]

[1]华东师范大学数学系，数学分析(上册)[M].4版.北京：高等教育出版社，2010：231.

[2]华东师范大学数学系，数学分析 (下册)[M].4版.北京：高等教育出版社，2010：16，52.

The Convergence of the Power Series ofarcsinx

WANGLi-Mei,PENGYi-ming,WANGHao

(University of International Business and Economics, Beijing 100029, China)

Abstract:We use three different methods, including Raabe Test, Wallis figure and elementary analysis, to obtain the convergent domain of the power series of the functionarcsinx. As an application of the result, we get the sum of a special constant series.

Key words:convergence of power series； Raabe Test； Wallis figure

[基金项目]数学天元基金(11326080)

[收稿日期]2014-05-15

[中图分类号]O173

[文献标识码]C

[文章编号]1672-1454(2015)01-0056-03