CE-Bézier曲线与二次均匀B样条曲线的拼接

洪　玲，　邢　燕

(合肥工业大学数学学院，安徽合肥230009)



CE-Bézier曲线与二次均匀B样条曲线的拼接

洪玲，邢燕

(合肥工业大学数学学院，安徽合肥230009)

[摘要]将B样条曲线转换为Bézier曲线，基于Bézier曲线间的光滑拼接的理论，研究了带多形状参数的Bézier曲线(CE-Bézier曲线)与均匀B样条曲线的拼接问题，得出均匀B样条曲线与CE-Bézier曲线的G0，G1，G2光滑拼接条件.在达到拼接条件的前提下，通过改变CE-Bézier曲线的形状参数的数值大小，可以灵活调整拼接曲线的形状.

[关键词]CE-Bézier曲线； 均匀B样条； Bézier构造方法； G2连续拼接

1引言

Bézier曲线和均匀B样条曲线(UniformB-splinecurves)是计算机辅助几何设计(CAGD)等领域表示和设计自由曲线方面的重要研究内容[1]，但随着几何造型工业的快速发展，特别是在新工业产品设计的要求下，原有的Bézier方法和B样条方法都很难满足曲线、曲面的几何造型需求.近几年有许多曲线设计人员通过引入参数、对伯恩斯坦基和B样条基进行扩展，构造一些类似伯恩斯坦基和B样条基性质的基函数，这样可以便捷地改变曲线、曲面的形状，增加其灵活性、形状可调性和逼近性.因此，带形状参数的Bézier曲线和B样条曲线的扩展研究如今成为计算机辅助几何设计中的热点问题.

近年来，人们对通过形状参数来调整曲线曲面的形状产生了兴趣：文献[2]在文献[3]的基础上提出了带一个形状参数参数的n次Bézier曲线，因为只带一个形状参数的曲线，在对曲线进行调控时，曲线只能在上下移动.为了更好地调控曲线，文献[4]构造了一类带双参数的二次三角Bézier曲线；文献[5]提出了带多形状参数的广义Bézier曲线曲面；文献[6]提出了三角域上带形状参数的三次Bézier曲面；文献[7]提出了两种新的分别带有2个和3个形状控制参数的三次扩展Bézier曲线，统称为CE-Bézier曲线，CE-Bézier曲线不仅具有三次Bézier曲线的特性，而且具有灵活的形状可调性和更好的逼近性，可灵活实现更多种逼近方式.

带形状参数的Bézier曲线、曲面应用非常广泛，然而在CAD/CAM中常会遇到复杂曲线、曲面的造型问题，通常我们采取的办法就是进行曲线、曲面的拼接.针对具有参数的Bézier曲线、曲面的拼接，近两年也有许多文章：λαβ-Bézier曲线与3次Bézier曲线的拼接条件[8]，带多形状参数的三次Bézier曲线曲面的光滑拼接[9]，三次TC-Bézier与H-Bézier曲线曲面的光滑拼接[10]等等.但在曲线光滑拼接的研究中，往往都是对带形状参数的Bézier曲线之间或者是带形状参数Bézier曲线与一般Bézier曲线之间的拼接，很少有对带形状参数的Bézier曲线与均匀B样条间的拼接.鉴于此本文以二次均匀B样条曲线与CE-Bézier曲线间的拼接为例，并给出它们间拼接的G0，G1，G2光滑拼接条件.

2CE-Bézier曲线的定义

CE-Bézier曲线是由秦新强和胡刚在研究扩展三次Bézier曲线时提出的[7]，从文献[7]，我们可知三次CE-Bézier曲线有很多优点，如优良的形状可调性和对控制多边形更好的逼近性，调整形状参数可灵活实现多种逼近方式，且形状参数的几何意义明显.更多的对不同形式多项式基函数的研究可参照文献[12-16].

定义1[7]给定4个控制顶点Pi∈n，其中n=2,3;i=0,1,2,3.对t∈[0,1]定义曲线

(1)

称式(1)所定义的四次多项式曲线为带形状控制参数α,β,γ的三次扩展Bézier曲线，简称CE-Bézier曲线.其中四次多项式调配函数Bi,4(t)(i=0,1,2,3)定义如下：

(2)

式(2)中α,γ∈[-3,1]，β∈[-3,3]为形状控制参数.

显然，当参数α=γ,β=0时，曲线(1)退化为带单参数的三次Bézier曲线；而当参数β=0时，曲线(1)退化成带双参数的三次Bézier曲线.由式(1)，(2)不难推出CE-Bézier曲线具有如下性质：

(i) 端点性质

(ii) 凸包性；

(iii) 当α=γ,β=0时，曲线具有对称性；

(iv) 几何不变性和仿射不变性.

3B样条曲线与Bézier曲线的转换

二次均匀B样条转换为Bézier曲线，就是要找出两者的控制点之间的关系，只需令两条曲线的端点处的值和端点处的一阶导数值相等即可.

设给定的控制顶点为Q0,Q1,Q2，则二次Bézier曲线可表示为

(3)

其中u∈[0,1].

设给定的控制顶点为V0,V1,V2，则二次均匀B样条曲线可以定义表示为

(4)

其中u∈[0,1].

令二次Bézier曲线的端点及端点切矢分别等于二次均匀B样条曲线的端点及端点切矢

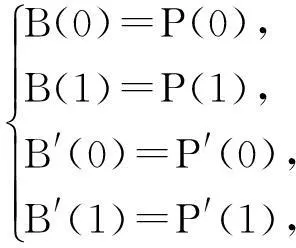
则有

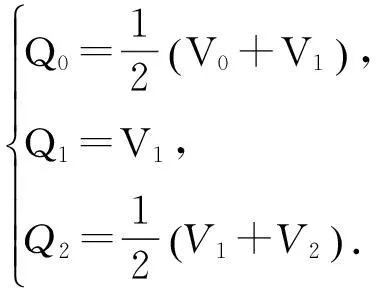
(5)

将(5)式代入(3)式，可得B(u)=P(u).

要将更高次的均匀B样条转化为Bézier曲线，可以利用转化矩阵[17].

4拼接定理

设由式(1)所定义的一条CE-Bézier曲线P(t,α,β,γ)，其控制顶点为P0,P1,P2,P3，则

式中Bi,4(i=0,1,2,3)由式(2)中所定义.

二次均匀B样条曲线P(u)如(4)式所定义，控制顶点为V0,V1,V2.利用上述二次均匀B样条曲线的Bézier构造方法，有

其中Qi(i=0,1,2,3)如(5)式所定义，则CE-Bézier曲线P(t,α,β,γ)与二次均匀B样条曲线P(u)的拼接就转化为CE-Bézier曲线P(t,α,β,γ)与二次Bézier曲线之间的拼接.

4.1　G0光滑拼接

定理1CE-Bézier曲线P(t,α,β,γ)与二次均匀B样条曲线P(u)的G0光滑拼接的充要条件是

当参数取值不一样时，两条曲线仍可以达到拼接条件.特别地，当α=β=γ=0时，就是普通的Bézier曲线(图中红色曲线)与二次均匀B样条曲线的拼接，如图1所示.红色，绿色，蓝色，青色和粉红曲线为不同形状参数下的CE-Bézier曲线，黑色为二次均匀B样条曲线.

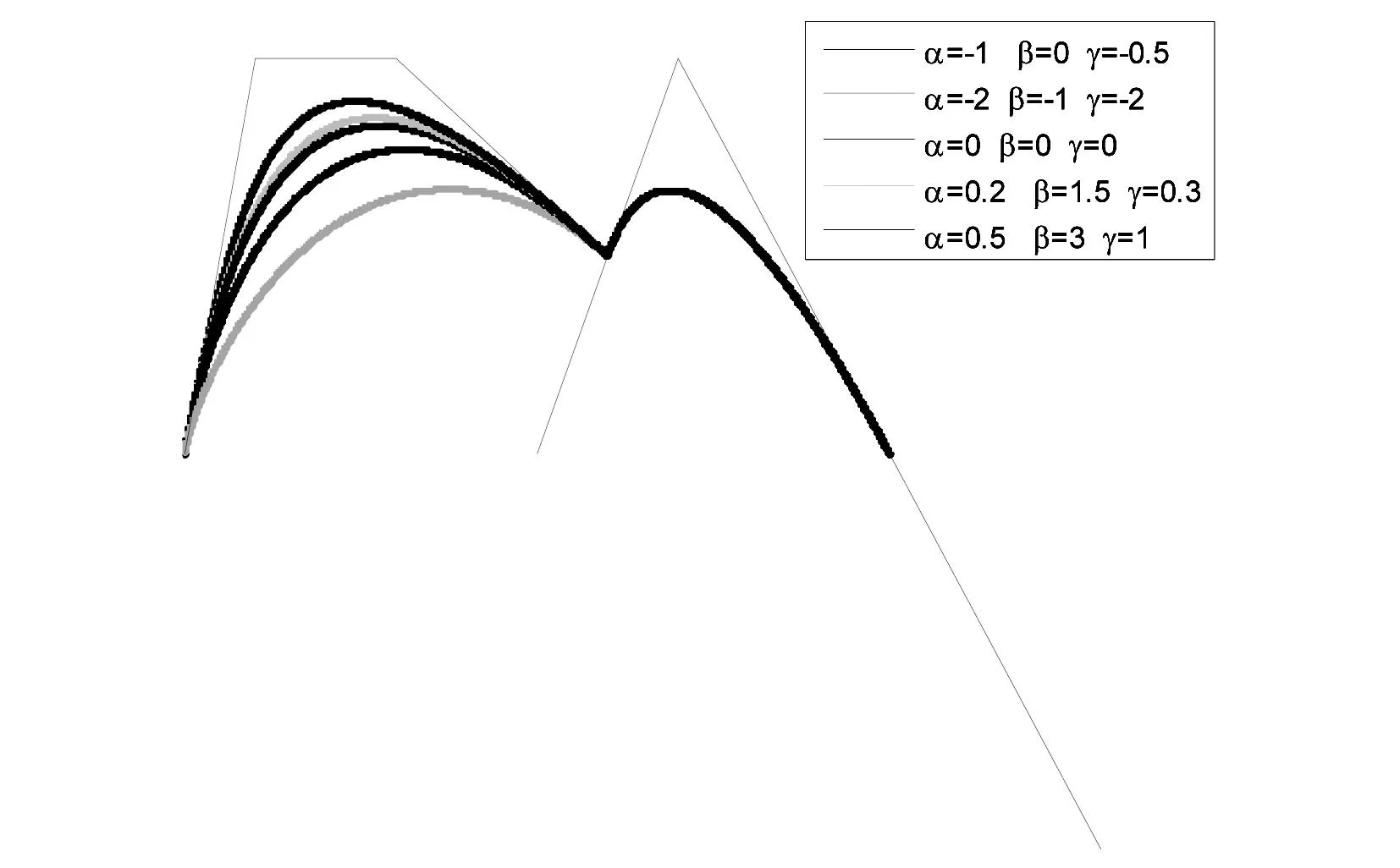
图1　曲线P(t,α,β,γ)与P(u)的G0光滑拼接

4.2　G1光滑拼接

定理2CE-Bézier曲线P(t,α,β,γ)与二次均匀B样条曲线P(u)的G1光滑拼接的充要条件是

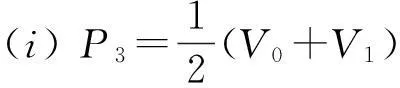
则曲线P(t,α,β,γ)与曲线P(u)在公共连接点处达到G1光滑拼接.

证为了让两条曲线达到G1连续，首先是G0连续，在定理1中我们已经给出了条件(i)的证明，在此我们只需证明条件(ii)即可.两曲线在公共连接点处有G1连续，其次还需两曲线在连接点处的切矢方向相同，即

P′(1,α,β,γ)=κP′(0)(κ>0).

由式(ii)可知P′(1,α,β,γ)=(3+γ)(P3-P2)，由式(5)可知P′(0)=V1-V0，则有

(3+γ)(P3-P2)=κ(V1-V0)，

两条曲线达到G1光滑拼接的图形如图2所示.当CE-Bézier曲线参数取不同值时，仍可达到G1连续.

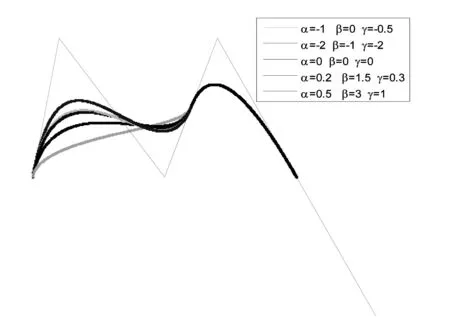
图2　曲线P(t,α,β,γ)与P(u)的G1光滑拼接

4.3　G2光滑拼接

定理3在满足G1连续的条件下，如果还满足

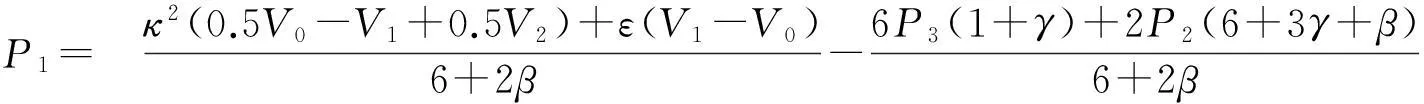
则CE-Bézier曲线P(t,α,β,γ)与二次均匀B样条曲线在公共连接点处有G2光滑拼接，其中κ如定理2中定义，ε为任意数.

证由曼宁的G2光滑拼接条件，除了满足G1光滑条件外，还需在连接点处满足曲率连续条件

P″(1,α,β,γ)=κ2P″(0)+εP′(0).

(6)

由上文可知

P″(1,α,β,γ)=6(P3-2P2+P1)+6γ(P3-P2)+2β(P1-P2)，

P″(0)=0.5V0-V1+0.5V2，P′(0)=V1-V0.

由(6)式，即有

CE-Bézier曲线与二次均匀B样条曲线的G2拼接如图3所示.

图3　曲线P(t,α,β,γ)与P(u)的G2光滑拼接

5结束语

本文研究了一种重要的带多形状参数的三次扩展Bézier曲线—CE-Bézier与二次均匀B样条的拼接，首先利用B样条曲线的Bézier构造方法，把二次均匀B样条曲线转化为二次Bézier曲线，然后再讨论了CE-Bézier曲线与二次Bézier曲线的拼接条件.由于第二类CE-Bézier曲线不仅具有更好的逼近性和更灵活的逼近方式，而且计算相对简单.

本文中给出了CE-Bézier与二次均匀B样条的G0,G1,G2拼接条件，在达到拼接的前提下，取不同的参数值，可以灵活调整拼接曲线的形状，相信对曲线设计人员有一定帮助.

[参考文献]

[1]施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京：高等教育出版社, 2001：21-27.

[2]刘植. Bézier 曲线的扩展[J]. 合肥工业大学学报(自然科学版), 2004，27(8): 976-979.

[3]吴晓勤, 韩旭里. 三次Bézier曲线的扩展[J]. 工程图学学报, 2005, 26(6): 98-102.

[4]谢进, 邬弘毅. 一类带双参数的二次三角Bézier曲线[J]. 合肥学院学报(自然科学版), 2006, 16(1): 20-23.

[5]刘植, 陈晓彦, 江平. 带多形状参数的广义Bézier曲线曲面[J]. 计算机辅助设计与图形学学报, 2010，5(5): 838-844.

[6]刘植, 檀结庆, 陈晓彦. 三角域上带形状参数的三次Bézier曲面[J]. 计算机研究与发展, 2012, 49(1): 152-157.

[7]秦新强, 胡钢, 张素霞. 三次Bezier曲线的新扩展及其应用[J]. 计算机工程与应用, 2008, 44(2): 112-115.

[8]杨林英, 张贵仓. λαβ-Bézier曲线与3次Bézier曲线的拼接条件[J]. 江西师范大学学报(自然科学版), 2011(11):621-623.

[9]胡钢, 张念娟, 秦新强, 等. 带多形状参数的三次Bézier曲线曲面的光滑拼接[J]. 西安理工大学学报, 2009, 25(4): 482-486.

[10]喻德生, 刘烨. 三次TC-Bézier与H-Bézier曲线曲面的光滑拼接[J]. 南昌航空大学学报(自然科学版) , 2011, 25(2):7-11.

[11]张贵仓, 杨林英, 胡志涛, 等. 三次Bézier曲线与二次均匀B样条曲线的光滑拼接[J]. 西北师范大学学报(自然科学版), 2012，48(5):28-31.

[12]Han X. Quadratic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design, 2002, 19(7): 503-512.

[13]邬弘毅, 陈晓彦.多形状参数的三次非均匀三角多项式曲线[J]. 计算机辅助设计与图形学学报, 2006, 18(10): 1599-1606.

[14]Han X A, Ma Y C, Huang X L. The cubic trigonometric Bézier curve with two shape parameters [J].Applied Mathematics Letters, 2009, 22(2): 226-231.

[15]Han X A, Huang X L, Ma Y C. Shape analysis of cubic trigonometric Bézier curves with a shape parameter [J]. Applied Mathematics and Computation, 2010, 217(6): 2527-2533.

[16]喻德生, 徐迎博, 曾接贤. 一类双参数类四次三角Bézier 曲线及其扩展[J].计算机工程与应用 2013, 49(18):180-186.

[17]徐少平, 白似雪, 薛之昕, 等. B样条与Bézier曲线转换矩阵的快速计算方法及应用[J]. 计算机应用与软件, 2008, 25(7): 91-93.

Research on Smooth Connection between CE-Bézier

Curves and Quadratic B-spline Curves

HONGLing，XINGYan

(School of Mathematic, Hefei University of Technology, Hefei 230009, China)

Abstract:Based on the theory of curves’ smooth connection, the paper researched the connection problem between Bézier curves with multiple shape parameters (CE-Bézier) and uniform B-spline curves, through converting B-spline curves to Bézier representation. The necessary and sufficient conditions of G0,G1,G2splicing between CE-Bézier curves and uniform B-spline curves were proposed. After meeting the splicing conditions, by changing the shape parameters of CE-Bézier curve, the shape of the stitching curve can be adjusted flexibly.

Key words:CE- Bézier curve; Uniform B-spline; Bézier constructive method; G2- continuity splicing

[基金项目]国家自然科学基金青年基金(61100126)；安徽省自然科学基金(1308085MA09)；合肥工业大学横向课题(JY13-014)

[收稿日期]2014-07-01

[中图分类号]TP391

[文献标识码]A

[文章编号]1672-1454(2015)01-0026-05