关于一大类第二型曲线积分问题的教学札记

姚　磊,　姚云飞,　王先超

(1.中央财经大学金融学院，北京100081；　2.阜阳师范学院经济学院，安徽阜阳236032；

3.阜阳师范学院数学与统计学院，安徽阜阳236032)



关于一大类第二型曲线积分问题的教学札记

姚磊1,2,姚云飞3,王先超3

(1.中央财经大学金融学院，北京100081；2.阜阳师范学院经济学院，安徽阜阳236032；

3.阜阳师范学院数学与统计学院，安徽阜阳236032)

[摘要]曲线积分计算往往存在技术性的困难，若利用“正交变换” (二次型)”等有关理论去解决这些计算问题，则往往有功效。文[1],[2]给出了正交变换(二次型)在重积分中应用。现将在多年的教学实践中，以“正交变换”为工具，处理了二元二次型的面积问题，简捷的处理了一大类第二型曲线积分的问题的教学方法整理出来。这些方法与结果不但对从事大学数学教学有一定的实用性，而且对从事金融数学的教学研究也有着一定参考价值.

[关键词]教学实践； 问题解决； 整体思路； 创新能力

大家知道，大学理科、工科、经济学、金融学、金融工程等专业的学生 ，从大学一年级开始，循序渐进的学习高等数学、解析几何学、线性代数学等数学课程的内容，为学习专业课程打基础.多年教学实践告诉人们各自学习一门课程较为容易接受，但是在实践中、在应用中往往需要将各门课程之间的关系打通，综合应用方能解决实际问题往往感到困难.这是因为正像著名的数学家陈省身先生所说的“就在于科学本身的整体性”.试问在一个具体的问题的教学中，怎样综合应用多科知识来解决问题？本文将以较复杂有一定难度的高等数学(微积分学)中的第二型曲线积分问题为例论之：欲解决第二型曲线积分问题，需解决二次型的几何度量问题，欲解决二次型的几何度量问题，需用正交变换为工具方可.现将我们在多年教学中的做法总结如下，敬请同行斧正.

1开门见山摆出问题见新忆学寻找思路

例如求第二型曲线积分

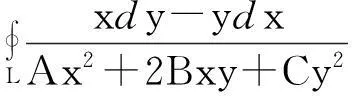
(其中L为xOy平面上的一条不经过原点分段光滑封闭曲线，方向为逆时针，A>0，AC-B2>0)的值.学生初见到这个问题时，往往感觉到难或者是“丈二和尚摸不着头脑”.于是启发学生，从简单(源头)出发，当题中分母的字母A=1,B=0,C=1,则问题成为求

的值.这个曲线积分问题在教材中是以例题的形式出现的，而解决这个问题的办法是否适应这个新问题呢？通过仔细分析，启发学生见新问题时，回忆所学过的课程(甚至是别的学科的课程)的有利于解决新问题的内容与方法，从而悟出解决新问题的整体(系统)思路，综合应用，他山之石，可以攻玉.其具体方法如下.

2着眼长远举一反三触类旁通建立引理

在教学中，让学生练习解决问题时，“不能头疼医头，脚疼医脚”，关键是培养学生的“着眼长远，举一反三，触类旁通”的能力，能够批量的解决一大类问题或几大类问题.为此给出了如下的引理，系统的处理了一批问题，获得了很好的结果.

本文约定

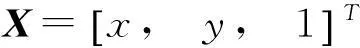
XT表示矩阵X之转置，矩阵A的行列式记为|A|(有时记为detA).本文约定矩阵A的元素aij的代数余子式记为Aij.

引理[5]设aij=aji,i,j=1,2,3.

f(x,y)=a11x2+2a12xy+a22y2+2a13x+2a23y+a33=XTAX.

证第一步证明f(x,y)经过平移后成为

第二步证明f(x,y)经过正交变换后(平移与旋转)后成为

第三步证明{(x,y)|f(x,y)≤0,x∈,y∈}在欧氏平面2中的面积为

(i) 第一步之证.因为

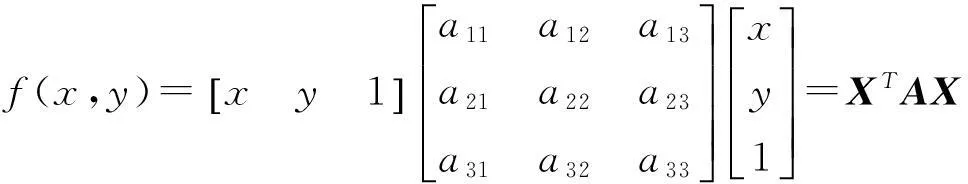
由B正定知A33≠0，于是由此知下面方程组有唯一解x0,y0.

解得

于是据aij=aji和文[3]中P79的定理3知

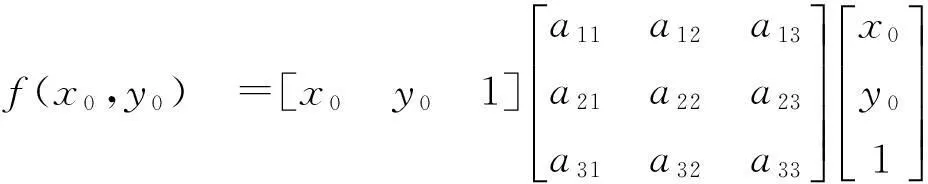
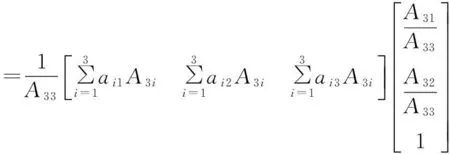
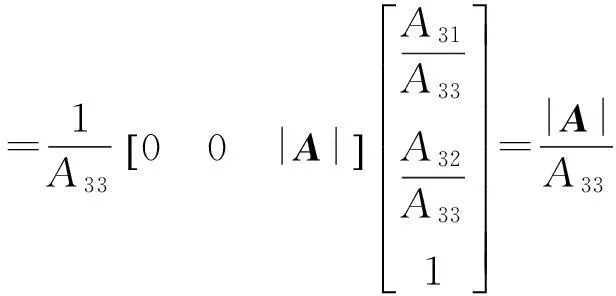
而平移后二次项系数不发生变化，事实上令x′=x-x0,y′=y-y0，则x=x′+x0,y=y′+y0，于是据AT=A与矩阵运算法则及其上述推理知

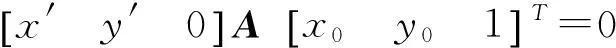
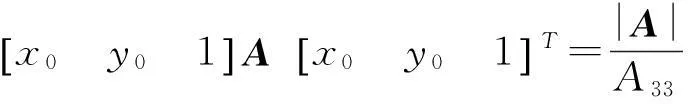
故

f(x,y)=f(x′+x0,y′+y0)

=[x′+x0y′+y01]A[x′+x0y′+y01]T

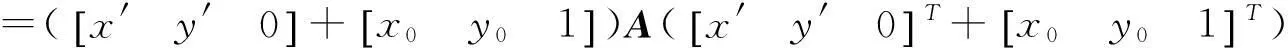
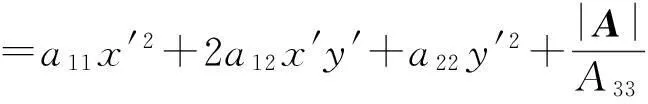
则由第一步之证的结果知

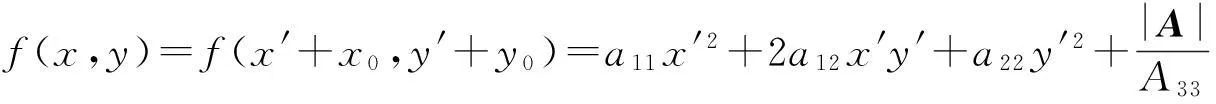
于是由文[3]中P380定理8知存在正交变换使

a11x′2+2a12x′y′+a22y′2=λ1u2+λ2v2,

故

a11x2+2a12xy+a22y2+2a13x+2a23y+a33.

经过两步正交变换(平移与旋转)一定可以化成

其中λi为矩阵B的特征值，且由矩阵B的正定性知λi>0,i=1,2, 其中由高等代数知识知

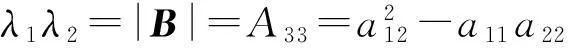
于是由{f(x,y)≤0}知

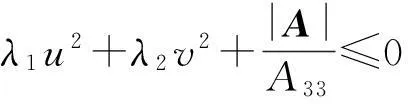
从而

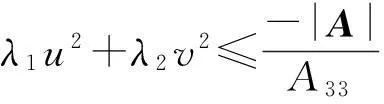
由此知

(*)

因为{(x,y)|f(x,y)≤0,x∈,y∈}记其为Ω,记

因为正交矩阵的行列式的值之绝对值等于1，所以正交变换σ的雅可比行列式的值之绝对值

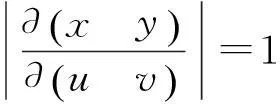
于是依据重积分的几何意义与变量替换定理[4]知

(**)

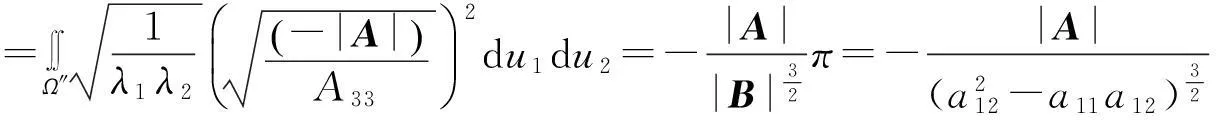
注1此引理即为[5]中P195的问题7，其较[5]中的处理方法简单，由此引理可得下面的特例.

特例

当AC-B2>0，C>0，ε>0时，则

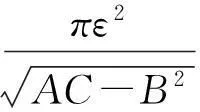
3居高临下势如破竹问题解决培养创新

为了解决本文一开始提出的问题，关键处理好其分母是二次型的问题及其几何度量的问题，我们已在本文“2”中解决了.于是可以居高临下势如破竹使一大类问题获得解决，培养了学生的创新能力.

问题1[4]若①L为xOy平面上的一条不经过原点分段光滑封闭曲线，方向为逆时针，

②A>0,AC-B2>0,

则(i)当L包围原点时，

(ii) 当L不包围原点时，

证由A>0，AC-B2>0知二次型Ax2+2Bxy+Cy2正定.于是

Ax2+2Bxy+Cy2=0 ⟺x=y=0.

因此当L不包围原点时Ax2+2Bxy+Cy2≠0.因为

从而

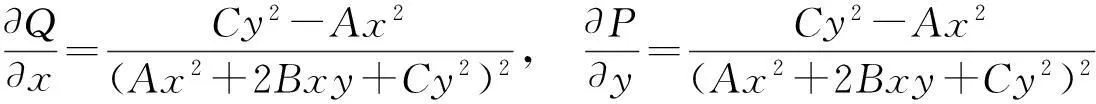
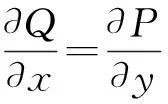
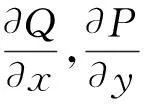
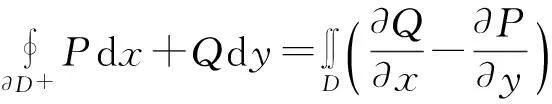
而

于是

进而

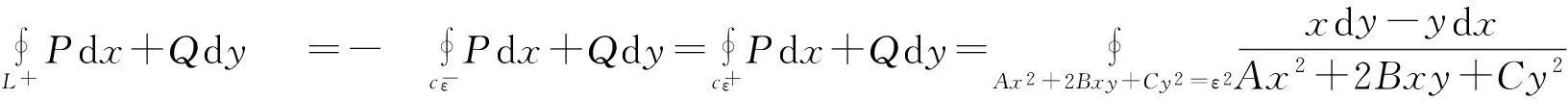
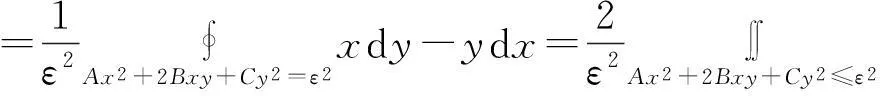
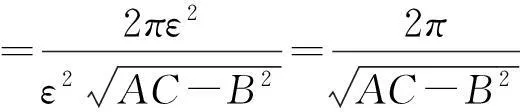
综上所述知(i)与(ii)成立.

注问题1具有非常好的包容性，好多文献中的问题及其近年来的考研试题与国内外的大学生数学竞赛试题，往往出现其特例问题.利用本问题1可以系统化的解决许多文献中的问题.例如从问题2到问题10：

问题2当A=1,B=0,C=1,L同问题1，则[6-8]

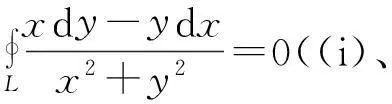
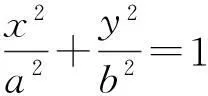
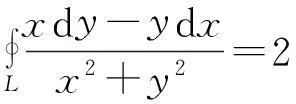
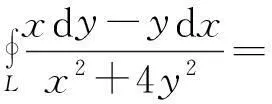
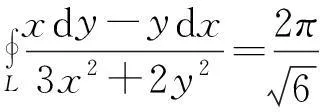
问题7[4]当L为xOy平面上的一条不经过原点分段光滑封闭曲线，方向为逆时a,b,c,d∈,ad≠bc，则(i) 当L包围原点时，

(ii) 当L包围原点时，

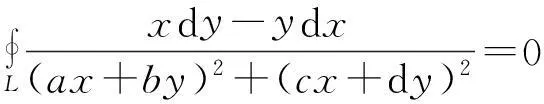
问题8(厦门大学2005年考研试题、[6]P434问题4321.)设X=ax+by,Y=cx+dy,ad-bc≠0，且L为包围坐标原点的简单封闭曲线，则

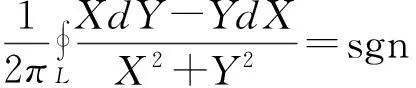
问题9[6-7]可以将问题6,7推广到下面问题之中,若

(i) 简单的围线L包围坐标原点，

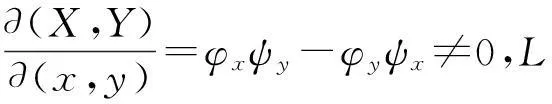
问题10Gauss积分[8]

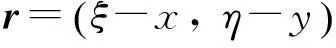
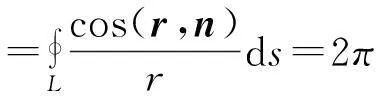
4结束语

上述是我们多年来的教学实践中的一些解决批量问题的革新的整体思路的居高临下势如破竹的做法.有效的提高了课程教学的质量，有效的开发了学生的智能，有效的培养了学生的创新的能力.

[参考文献]

[1]姚云飞. 正交变换在重积分中某些应用[J].数学的实践与认识,2003, 33(9):139-144.

[2]姚云飞. 论二次型与正交变换在重积分中的某些应用[J].工科数学,2002,18(6):90-102.

[3]北京大学数学系前代数小组编，王萼芳，石生明修订高等代数[M].4版.北京：高等教育出版社,2013：79，206-233，355-394.

[4]胡适耕,姚云飞.数学分析：定理.问题.方法[M]. 北京：科学出版社,2007：166-167.

[5]TM菲赫金哥尔茨.微积分学教程二卷一分册[M]. 北京大学高等数学教研室译.北京：人民教育出版社，1978：194-196，209-210.

[6]BII吉米多维奇.数学分析习题集[M]. 李荣冻译.北京:人民教育出版社,1978：219，224，389.

[7]黄定晖，周学圣. B II吉米多维奇数学分析习题集解(六)[M].济南：山东科技出版社，1980：271-275.

[8]TM菲赫金哥尔茨著.微积分学教程三卷一分册[M]. 路见可译.北京：人民教育出版社，1978：56-58.

[9]钟玉泉.复变函数论[M]. 北京：高等教育出版社，2010：100，103-110.

[10]Polga G, Sego G. Problems and Theorems in Analysis[M]. Berlin:Springer-Verlag, 1972：143-145.

Teaching Notes on the Problems of the Second Type Curve Integral

YAOLei1,2,YAOYun-fei2,WANGXian-chao2

(1.School of Finance,Centyral University of Finance and Economics, Beijing 100081, China;

2.School of Economics , Fuyang Teachers College, Fuyang Anhui 236037,China;

3.School of Mathematics and Statics , Fuyang Teachers College, Fuyang Anhui 236037,China )

Abstract:There exists technique difficulties in calculating curve integrals, but it is often effective by using orthogonal transformation (quadratic form) theory to solve these problems. References [1] and [2] gave the applications of the orthogonal transformation (quadratic form) in multiple integral. Through many years’ teaching experience, we treats area problems ofbinary quadratic forms by using orthogonal transformation and successfully resolved many problems of curve integrals. These methods and results are of reference value to the teaching research of finance mathematics.

Key words:teaching practice; problem solving; whole thought; innovative ability

[中图分类号]O151.2； O172.2

[文献标识码]C

[文章编号]1672-1454(2015)05-0076-07

[基金项目]国家特色专业(TS11496)； 全国统计科学计划项目(2011LY094)； 阜阳师范学院重点学科(2010XK-03)

[收稿日期]2015-08-02