随机需求下单供应商与多零售商的生产—库存—运输联合优化模型

杨志林，　李擎卿，　林冠男，2

(1.合肥工业大学数学学院，合肥230009；　2.南昌工学院基础教学部，南昌330108)



随机需求下单供应商与多零售商的生产—库存—运输联合优化模型

杨志林1，李擎卿1，林冠男1，2

(1.合肥工业大学数学学院，合肥230009；2.南昌工学院基础教学部，南昌330108)

[摘要]考虑随机需求下单供应商和多零售商的生产-库存-运输联合优化问题.在独立决策时，各零售商独立决策其最优订货量和最优订货点，供应商根据各零售商的决策来为之配送.在联合决策时，由供应商统一决策各零售商的送货量和送货时间，并基于此建立单供应商与多零售商的生产-库存-运输优化模型，利用粒子群算法和模拟退火算法相结合的两阶段算法求出最优送货量、最优运输路径和最大期望总利润.然后采用收入共享契约将增加的利润合理分配给供应商和各零售商，使各方利润都得到增加，从而促使各方愿意合作.最后，通过数值算例验证了联合优化模型优于独立决策模型.

[关键词]随机需求； 生产—库存—运输联合优化； 粒子群算法； 模拟退火； 收入共享契约

1引言

供应链管理能够增强供应链上各个企业的竞争力，优化资源配置，降低总成本，构建快速应对市场变化的能力.在21世纪，市场竞争已变成了这种供应链之间的竞争.生产、库存和运输是供应链中重要的组成部分，所以生产管理、库存管理和运输管理成为供应链管理中的三个重要方面，如何降低生产、库存和运输费用已成为优化供应链的关键，同时也是供应链的领域中的热点问题.

现有相关文献主要考虑了库存与运输优化问题或生产与库存优化问题，如刘桂庆等[1]是关于确定性需求下的单供应商与多零售商的库存和运输联合优化模型，Ozener等[2]、Shukla等[3]研究了随机性需求下的单供应商与单零售商的库存运输模型.Krishnamoorthy 等[4]和施文武等[5]探讨了随机性需求下生产库存优化模型.仅有很小部分文献将生产、库存和运输联合起来进行分析和研究，如Bard等[6]、缪周等[7]和Pan 等[8]针对确定性需求，建立了单供应商与多零售商的生产、库存和运输模型，并没有考虑随机性需求情形下的单供应商与多零售商的生产-库存-运输联合优化模型.Bard[9]针对随机性需求，研究了单供应商与单零售商的生产、库存和运输模型，但其拓扑结构较为简单，并没有扩充到单供应商对多零售商的供应链结构.

基于以上分析，本文将针对随机性需求，考虑单供应商与多零售商的生产-库存-运输联合优化问题，同时考虑允许零售商缺货，且部分缺货可延期交付，使之更符合实际市场行为.在生产、库存与运输三部分费用之间做出合理的平衡，以探求全局最优的生产-库存-运输联合优化方案，最终建立随机需求下单供应商与多零售商生产-库存-运输联合优化模型.

2假定及符号说明

假设零售商的需求是随机的，允许零售商缺货，且部分缺货可延期交付，部分缺货发生销售损失；同时考虑运输成本由供应商支付.

πs，πri，πsc——供应商、零售商i、供应链的单位时间的利润；

p——供应商单位产品的生产成本；

w——零售商单位产品的批发价格 ；

c——零售商单位产品的零售价；

di——零售商i单位时间的需求量，是非负随机的，μi表示随机需求的期望，i=1，…，n；

qi——零售商i的最优订货量，i=1，…，n；

hi——零售商i的单位时间单位产品的库存成本，i=0，…，n(h0为供应商的单位时间单位产品的库存成本)；

si——零售商i的单位产品的缺货惩罚费用，i=1，…，n；

K——零售商的订货费用；

A——供应商的生产设置成本；

Qv——车辆容量；

M——车辆启动成本；

m——联合决策时所需要的车辆数目；

a ——车辆行驶单位距离的运输成本；

lij——从点i到点j的距离，i,j=0…n(0点代表供应商)；

β——缺货期间允许零售商延期交货的比例，1-β则为销售损失的比例，0≤β≤1；

o——单位物品的边际收益.

3独立决策情形下的数学模型

零售商i单位时间的期望订单成本为Kμi/qi.

因此，零售商i单位时间的期望总利润

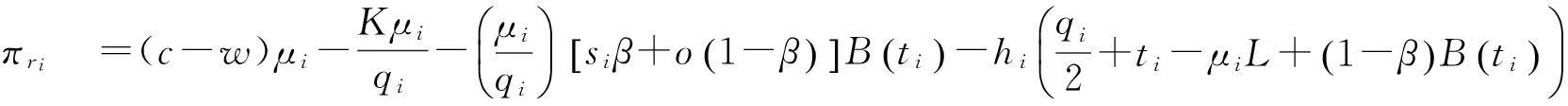
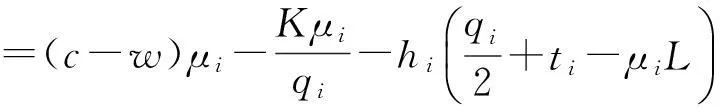
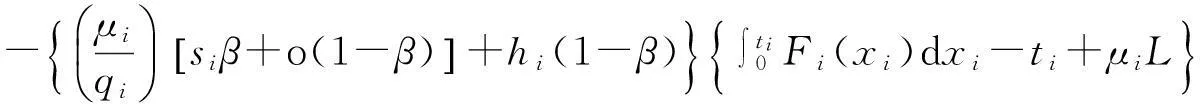
(1)

由一阶最优性条件得

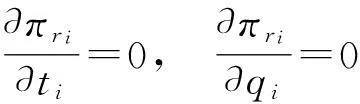
Step2：将qi=qi1代入式(2)求ri1.

Step3：将ri=ri1代入式(3)求qi2.

Step4：将qi2代入式(2)，迭代到收敛为止.

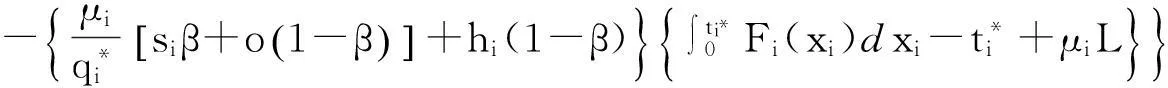
(4)

单位时间供应商对于零售商i的利润

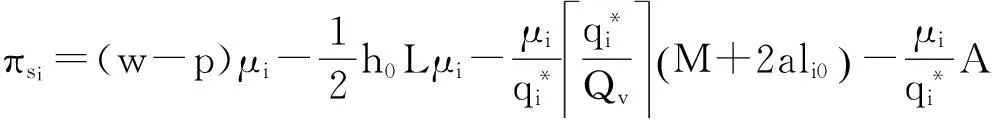
πsi=(w-p)μi-12h0Lμi-μiq*iq*iQvM+2ali0()-μiq*iA

q*iQv

为运送零售商i产品所需的车辆数.所以，单位时间供应商的期望总利润为

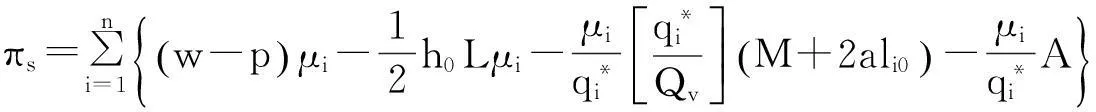
(5)

从而，单位时间供应链的期望总利润为

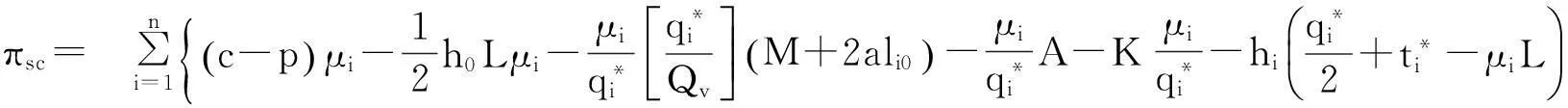
(6)

4联合决策下的数学模型

联合决策情形下的供应商为各个零售商的送货周期均为T，各点的送货量为Qi，设零售商i在T内的需求量yi是一个非负随机变量，其概率密度函数和分布函数分别为gi(yi)和Gi(yi)，则μiT表示随机需求的期望.

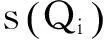
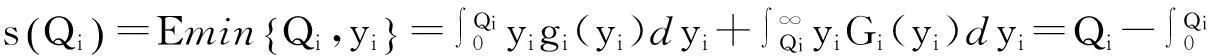
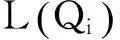
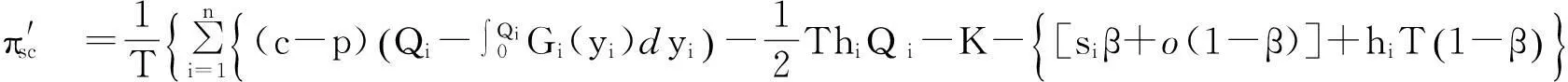
(7)

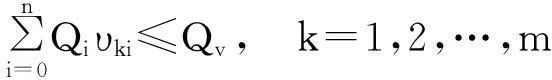
(8)

(9)

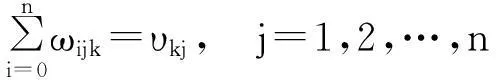
(10)

(11)

ωijk=1或0,i,j=0,1,2，…，n； k=1,2,…，m，

式(8)为车辆最大载重量约束，即每辆车的实际装载量不能超过车辆的最大载重量；式(9)保证了每个零售商的任务仅由一辆车完成；式(10)和(11)表示车k在进行服务时，对每个零售商服务且只服务一次，即车k确定服务范围后，安排路线时确保经过且仅经过它服务范围内的每个零售商一次.

5联合决策下的算法设计

由于本问题是NP难问题，难以用传统的精确算法求解，因此本文采用了粒子群算法[12]和模拟退火算法[13]相结合的两阶段算法，用于求解随机需求下的生产—库存—运输联合优化模型.

第二阶段：用粒子群算法经过迭代求得联合决策下的供应链的最大利润和各个点的送货量Qi.

其中(i) 模拟退火算法的具体步骤如下

Step1:设置控制参数，包括初始温度T0、温度衰减系数α、终止温度tf、当前温度迭代次数u、当前成功迭代次数l.

Step2:随机产生可行解f0，令fi=f0.

Step3:构造邻域解.在一条路径中随机选取两个零售商，r为(0,1)之间的随机数，若r<0.65，则交换两个零售商，得到一条新的路径;否则，将两个零售商之间的节点逆序， 得到一条新的路径.按照上述方法将得到邻域解记为fj，且令u=u+1.

Step4:比较.如果fj≥fi，则转Step5 ; 否则fj=fi，记录当前解为最优解，l=l+1 ，转Step6 .

Step6:温度下降规则.若u≥U或l≥L，Ti+1=αTi，u=0，l=0，转Step7;否则返回Step3 .

Step7:算法终止规则.若当前温度Ti+1≤tf，算法终止;否则返回Step3 .

(ii) 粒子群算法的具体实现步骤如下：

Step1：初始化粒子群、惯性因子ω、加速常数c1,c2、最大迭代次数和算法终止的最小误差.

Step2：用评价函数评价所有粒子的初始适应值.(其中，评价函数为联合决策下供应链总利润的倒数)

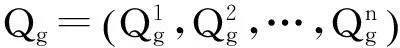
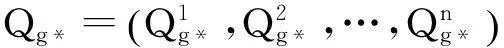
Step6:对每个粒子的飞翔速度进行限幅处理，使之不能超过设定的最大飞翔速度.

Step8:比较当前每个粒子的适应值是否比历史局部最优值好，如果好，则将当前粒子适应值作为粒子的局部最优值，其对应的送货量作为每个粒子的局部最优值对应的送货量.

Step9:在当前群中找出全局最优值，并将当前全局最优值对应的送货量作为粒子群的全局最优值对应的送货量.

Step10:重复步骤Step5～Step9，直到满足设定的最小误差或者达到最大迭代次数.

Step11:输出粒子群全局最优值和其对应的各点送货量.

6收入共享契约下的协调策略

已知联合决策的单位时间供应链的总利润为π′sc，独立决策下单位时间供应链的总利润为πsc，则单位时间供应链增加的利润为Δπsc=π′sc-πsc.若Δπsc>0，说明联合决策可以提高供应链利润，则需设计合理的协调策略来分配增加的利润.

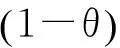
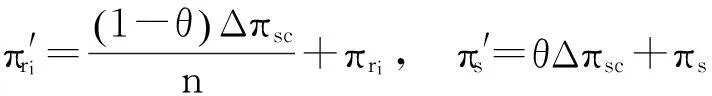
7算例

有1个供应商(编号为0)，提供单产品，有7个零售商(编号为1到7)，K=200，A=1500，T=L=56/365，M=100，a=5，Q=1000由实际情况可知零售商的销售量服从指数分布，即

解按照上面提供的算法利用Matlab编程进行实验，为了观察缺货期间允许零售商延期交货的比例β对实验结果的影响，可对β取不同的值观察实验结果.因为0≤β≤1，取其端点值0和1，再从(0,1)内任取两个值，不妨取β=0.5和β=0.8，其算例结果见表2和表3.

对比表2和表3可以发现，β=0,β=0.5,β=0.8以及β=1时联合决策后供应链的利润都大于独立决策时的利润，即单位时间的供应链利润增加了，也就说明联合决策可以提高供应链利润，从而采取收入共享契约下的协调策略时，能够确保供应商与零售商愿意合作，使得供应链达到最优.

表1　实验参数表

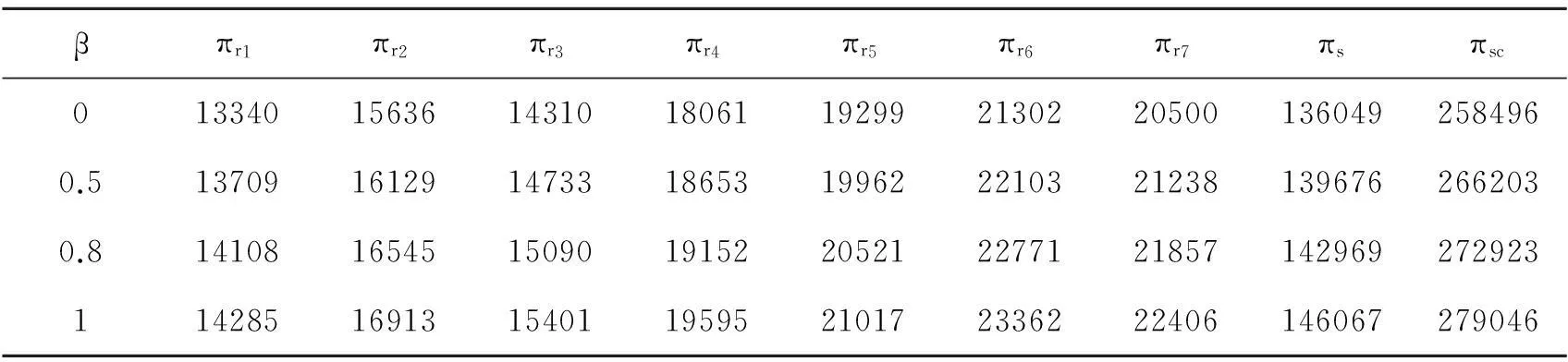
表2　独立决策实验结果

表3　联合决策实验结果(θ=0.4)

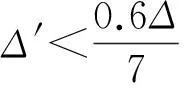
由以上数据，我们还可以发现，期望总利润随着β的增大而增加，这很容易理解，因为β越多就会有更多的客户愿意等待.除此之外，当θ值越大，分给供应商的利润越多；反之，分给零售商的利润越多.

8结论

本文研究了单供应商多零售商在面对随机需求下的生产-库存-运输问题，通过分析各零售商的订货费、库存费和缺货费，供应商的库存费、运输费等，建立供应商与零售商期望总成本最小化模型，通过收入共享契约使得供应商和零售商的利润同时增加,同时针对问题模型给出了优化解决的算法, 这对企业在降低物流成本和制定相关策略时具有重要的指导意义.将来可进一步研究的方向有：随机需求下的多生产商和多零售商的生产-库存-运输问题、随机需求下多产品的单生产商和多零售商的生产-库存-运输问题等.

[参考文献]

[1]刘桂庆,周永务,李凯.基于价格策略的非一体化供应链IRP问题[J].系统仿真学报,2008,20(6):1408-1412.

[2]Ozener O O, Ergun O, Savelsbergh M.Allocating cost of service to customers in Inventory routing[J]. Operations Research,2013,61(1):112-125.

[3]Shukla N,Tiwari M K , Ceglarek D. Genetic-algorithms-based algorithm portfolio for inventory routing problem with stochastic demand[J]. International Journal of Production Research,2013,51(1):118-137.

[4]Krishnamoorthy A,Viswanath N C .Stochastic decomposition in production inventory with service time [J]. European Journal of Operational Research,2013,228(2):358-366.

[5]施文武,严洪森,汪峥.一种多周期随机需求生产库存控制方法[J]. 控制与决策,2007,22(9): 994-999.

[6]Bard J F, Nananukul N. The integrated production-inventory-distribution-routing problem[J]. Journal of Scheduling, 2009, 12(3):257-280.

[7]缪周,徐克林,朱伟.考虑运输—生产—库存集成的精益供应链模型[J].制造业自动化,2011,33(6):57-61.

[8] Pan F ,Nagi R .Multi-echelon supply chain network design in agile manufacturing [J]. Omega-international Journal of Management Science, 2013,41(6):969-983.

[9]Bard J F, Nanafalia N.The integrated production-inventory-distribution-routing problem[J]. Journal of Scheduling, 2009,12 (3): 257-280.JI X G, DENG Y Y, WANG P. Characters of atmosphere pressure, pure oxygen fixed bed gasification of seven kinds coal[J]. Clean Coal Technology, 2004, 25(4): 50-52.

[10]Pan J C,Chiao Y C,Lee C J.Inventory models with fixed and variable lead time crashing costs considerations[J]. The Journal of the Operational Research Society,2002,53(9):1048-1053.

[11]周永务,王圣东.库存控制理论与方法[M].北京:科学出版社,2009:280-293.

[12]张涛,张春梅,张玥杰.协同粒子群-模拟退火算法求解VRPSPD问题[J].系统管理学报, 2009,18(6):681-685.

[13]Banos R,Ortega J, Gil C,et al.A Simulated Annealing-based parallel multi-objective approach to vehicle routing problems with time windows[J]. Expert Systems With Applications,2013, 40(5):1696-1707.

[14]Palsule-Desai O D. Supply chain coordination using revenue-dependent revenue sharing contracts[J]. Omega-international Journal of Management Science, 2013, 41(4): 780-796.

Integrated Production-inventory-transportation Optimization Model under

Stochastic Demand with Single-vendor and Multi-retailer

YANGZhi-lin1，LIQing-qing1,LINGuan-nan1,2

(1. School of Mathematics, Hefei University of Technology, Hefei 230009, China;

2. Department of Basic Courses, Nanchang Institute of Science and Technology, Nanchang 330108, China)

Abstract:We consider the production-inventory-transportation optimization under stochastic demand with single-vendor and multi-retailer. In the decentralized decision scenario, each retailer independently decides its optimal order quantity and order time, and the supply makes the delivery based on retailers’ decision. In the centralized decision scenario, the supplier decides the distribution quantity and distribution time. Then the integrated production-inventory-transportation optimization model is built. This paper designs a two-phase algorithm combined with simulated annealing algorithm and particle swarm optimization, in order to obtain optimal distribution quantity, optimal routings and maximum expected total profit. Then a revenue-sharing contract is used and the increased profit is shared by the supplier and retailers, therefore, all of them are willing to cooperate with each other. At the end of the paper, a numerical result is given to show that the integrated optimization model is better than the decentralized decision model.

Key words:stochastic demand; integrated production-inventory-transportation optimization; particles warm optimization; simulated annealing; revenue-sharing contract

[中图分类号]O227

[文献标识码]A

[文章编号]1672-1454(2015)05-0012-08

[收稿日期]2014-02-04