牛顿运动定律中图象问题的把握和应用
冯兰

利用图象考查牛顿运动定律主要分两类动力学问题:1、若已知v-t图象,则利用图象确定不同阶段的a、v、t.然后由牛顿定律求解相关问题;2、若已知F-t图象,则利用图象确定不同时段的受力,然后由牛顿定律求出加速度再由运动定律求解相关问题.下面我们分三个层次来分析、处理该类考题.
一、与牛顿运动定律相关的v-t图象问题
该类问题处理的关键是:1、会应用牛顿运动定律分析物理模型;2、理解加速度与速度的关系;3、v-t图象中某点斜率的意义——加速度,斜率为正说明速度与加速度同向,斜率为负说明速度与加速度反向,关注斜率有突变的点;某段时间内图线与t轴围成的面积——位移.
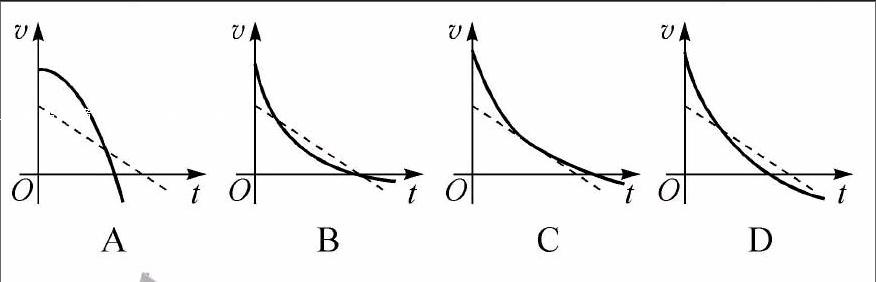
例1 以不同的初速度将两个物体同时竖直向上抛出并开始计时,一个物体所受空气阻力可以忽略,另一个物体所受空气阻力大小与物体的速率成正比,下列分别用虚线和实线描述两物体运动的v-t图象可能正确的是
()
解析 本题考查v-t图象.当不计阻力上抛物体时,物体做匀减速直线运动,图象为一条倾斜直线,因加速度a=-g,故该倾斜直线的斜率的绝对值等于g.当上抛物体受空气阻力的大小与速率成正比时,对上升过程,由牛顿第二定律得-mg-kv=ma,可知物体做加速度逐渐减小的减速运动,通过图象的斜率比较,A错误,从公式推导可知上升过程中|a|>g,当v=0时,物体运动到最高点,此时a=-g,而B、C图象的斜率的绝对值均小于g,故BC错误,D正确.
点拨 有阻力上抛运动中的动力学问题,图象特殊点的斜率.
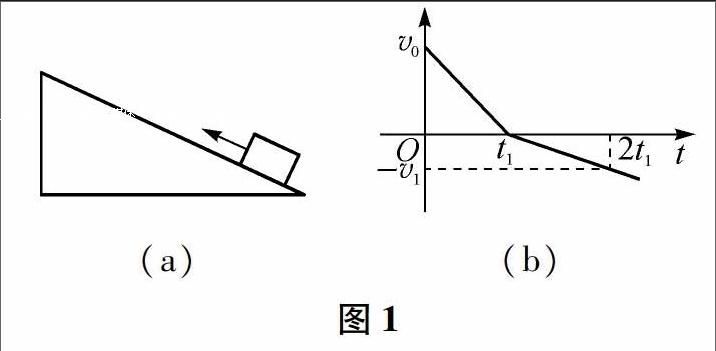
例2 如图l(a),一物块在t=0时刻滑上一固定斜面,其运动的v-t图线如图(b)所示.若重力加速度及图中的vo、v1、t1均为已知量,则可求出
()
A.斜面的倾角
B.物块的质量
C.物块与斜面间的动摩擦因数
D.物块沿斜面向上滑行的最大高度
解析 设物块的质量为m、斜面的倾角为0,物块与斜面间的动摩擦因数为μ,物块沿斜面上滑和下滑时的加速度大小分别为a1和a2,根据牛顿第二定律有:mgsinθ+μmgcosθ=ma1,mgsinθ-μmgcosθ=ma2.再结合v-t图线斜率的物理意义有:a1-vo/t1,a2=v1/tl.由上述四式可见,无法求出m,可以求出θ、μ,故B错,A、C均正确.o~t1时间内的v-t图线与横轴包围的面积大小等于物块沿斜面上滑的最大距离,θ已求出,故可以求出物块上滑的最大高度,故D正确,本题答案:ACD.
点拨:1.能对斜面上物体受力分析,会用牛顿第二定律列出表达式;2.图线斜率大小等于加速度大小,图线与横轴包围的面积大小等于位移的大小.
二、与牛顿运动定律相关的F-t图象问题
该类问题处理的关键是:除了在第一点中提到的要求外,还要能熟练地将F-t图、a-t图、v-t图联系起来.
例3 一质量为m=40kg的小孩在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在o到6s内体重计示数F的变化如图所示.试问:在这段时间内电梯上升的高度是多少?取重力加速度g=10m/S?.
解析 由图2可知,在O-2s内,体重计的示数大于mg,故电梯应做向上的加速运动.设在这段时间内体重计作用于小孩的力为Ⅳ.,电梯及小孩的加速度为a1,根据牛顿第二定律,得
Nl-mg=ma1
在这段时间内电梯上升的高度
在2-5s内,体重计的示数等于mg,故电梯应做匀速上升运动,速度为t1时刻的电梯的速度,即v1=a1t1,在这段时间内电梯上升的高度h2=v1t2
在5-6s内,体重计的示数小于mg,故电梯应做减速上升运动.设这段时间内体重计作用于小孩的力为N2,电梯及小孩的加速度为a2,由牛顿第二定律,得:
mg-f2=ma2
在这段时间内电梯上升的高度
电梯上升的总高度h=h1+h2+h3
代人数据解得h=9m
点拨:由F随时间的变化知道a随时间的变化进一步联系到速度随时间的变化.
解法二:这题可以根据F、a、v间的关系得到a-t图、v-t图(如图3所示),解题思路可以更清晰,解题过程也会更加简洁.
例4将力传感器A固定在光滑水平桌面上,测力端通过轻质水平细绳与滑块相连,滑块放在较长的小车上,如图4甲所示.传感器与计算机相连接,可获得力随时间变化的规律.一水平轻质细绳跨过光滑的定滑轮,一端连接小车,另一端系沙桶,整个装置开始处于静止状态.在滑块与小车分离前缓慢向沙桶里倒细沙,力传感器采集的F-t图象如图乙所示.则
()
A.2.5s前小车做变加速运动
B.2.5s后小车做变加速运动
C.2.5s前小车所受摩擦力不变
D.2.5s后小车所受摩擦力不变
解析 对滑块进行受力分析,由图象求出传感器对滑块的拉力,由平衡条件求出滑块受到的摩擦力,然后由牛顿第三定律判断小车的受力情况;根据图象可知,2.5s前滑块所受摩擦力随沙桶和细沙重力的增加而增加,可见此过程小车静止不动,故A、C均错;2.5s之后传感器拉力不变,说明此时小车开始运动,传感器拉力大小等于滑动摩擦力大小,因此2.5s后小车所受摩擦力不变,由于沙桶质量不断增加,2.5s后小车做变加速运动,故B、D正确.
点拨:找到传感器测得的F与小车受力的关系,理解F-t图象中力变化的意义.
三、与牛顿运动定律相关的F-t、v-t、a-t、x-t等图象的综合应用
要解决好此类综合问题,需要具有将物理现象转化为图象问题的能力.在综合题中由图象语言、函数语言和文字语言,我们要能够在任意两种语言间转换,并将语言与物理情景结合,以确立准确的解题方向,顺利地解决问题.
例5 固定光滑细杆与地面成一定倾角,在杆上套有一个光滑小环,如图5所示,小环在沿杆方向的推力F作用下向上运动,推力F与小环速度v随时间变化规律如图6所示,取重力加速度g=10m/S?.求:
(1)小环的质量m;
(2)细杆与地面间的倾角a.
解析 由图得a=v/t=0.5m/S?
前2s有 F1-mg sina=ma
2s后有F2=mg sina
代人数据可解得m=1kg,a=30°
点拨:理解两张图之间对应的关系.
例6 物体A、B、C均静止在同一水平面上,它们的质量分别为mA、mB、mc,与水平面间的动摩擦因数分别为μA、μB、μC,用平行于水平面的拉力F分别拉物体A、B、C,所得加速度a与拉力F的关系如图7所示,4、B两直线平行,则以下关系正确的是()
A.mA B.mA c.μA=μB=μC D.μA<μB=μC 解析 根据牛顿第二定律有: F-μmg=ma 所以有:a=F/m-μg 由此可知:图象斜率为质量的倒数,在纵轴上的截距大小为:μg 故由图象可知:μA<μB=μC,mA=mB 点拨:找到图象对应函数表达式. 例7 如图8所示,足够长的粗糙斜面固定在地面上,某物块以初速度vo从底端沿斜面上滑至最高点后又回到底端.上述过程中,若用h、x、v和a分别表示物块距水平地面的高度、位移大小、速度大小和加速度大小,t表示运动时间.下来图象中可能正确的是 () 解析 物理模型与实例2是一样的,但考查的图象知识、能力更全面. A.上滑时做匀减速运动,故h-t图线斜率先大后小,且平均速度大,运动时间短;下滑时做匀加速运动,故h-t图线先小后大,且平均速度小,运动时间长;故A正确. B.上滑时x-t图线斜率先大后小,下滑时x-t图线斜率先小后大,故B错误. C.由于上滑时合外力为重力分力和摩擦力之和,加速度大小不变,沿斜面向下;下滑时合外力为重力分力和摩擦力之差,加速度大小不变,方向沿斜面向下;所以上滑时加速度大,所以v-t图线斜率大;下滑时加速度小,所以v-t图线斜率小,且此过程中,摩擦力做功,使物块到达底端的速率变小,故C正确. D.因上滑过程中、下滑过程中的加速度大小均不变,且上滑时加速度大于下滑时的加速度,故加速度应该为两条水平短线,故D错误. 故选:AC. 点拨:牛顿第二定律的应用,能分析个各物理量间的联系及变化,各图象间的联系. 例8 如图9(a)所示,质量m=1kg的物体由静止开始沿倾角θ=37°的固定粗糙斜面向下运动,风对物体的作用力沿水平方向向右,其大小与风速v成正比,比例系数用k表示,物体加速度a与风速v的关系如图(b)所示(sin37°=0.6,cos37°=0.8,g取10m/S?).求: (1)物体与斜面间的动摩擦因数μ; (2)比例系数k. 解析 (1)由题图知v=0时,ao= 上述解法在解决本题时用了特殊值法,现在假设无法直接知道这两组特殊值,只知道截距和斜率,能解题吗?可以.就这个物理模型,对小物块进行受力分析,应用牛顿第二定律列出表达式: mgsinθ-kvcosθ-μ(mgcosθ+kvsinθ)=ma 代人数据得a与v的函数表达式: a=6-8μ-(0.8+0.6μ)kv 由截距的值b=6-8μ,斜率的值 |K|=(0.8+0.6μ)k 不难求出μ和k. 点拨:解决好此类问题的关键是找到图象中物理量的函数表达式. 物理公式与物理图象的结合是中学物理的重要题型,也是近年高考的热点,特别是v-t图象在考题中出现频率极高,对于已知图象求解相关物理量的问题,往往是结合物理过程从分析图象的横、纵轴所对应的物理量的函数人手,分析图象的斜率、截距所代表的物理意义得出所求结果.解决这类问题的核心是分析图象,我们应特别关注v-t图中的斜率(加速度)和力的图线与运动的对应关系.

