采用自适应模糊PID的二阶倒立摆控制

宋国杰

(四平职业大学 电子工程学院， 吉林 四平 136002)



采用自适应模糊PID的二阶倒立摆控制

宋国杰

(四平职业大学 电子工程学院， 吉林 四平 136002)

摘要：建立一个二阶倒立摆的数学模型，将常规比例-积分-微分(PID)控制与模糊控制相结合，设计模糊PID控制器，实现PID参数的自适应模糊整定.仿真实验表明：所设计的模糊PID控制器能很好地实现二阶倒立摆的扶起平衡控制，控制效果明显好于常规PID控制器，超调量和调节时间较小，具有较好的抗干扰能力，非常适合二阶倒立摆模型的稳定控制.

关键词：倒立摆； 模糊控制； 比例-积分-微分控制器； 自适应； 稳定控制

作为一个典型的不稳定、高阶次、强耦合、多变量非线性系统，倒立摆模型是控制领域内众多专家学者关注和研究的对象[1-2].通过倒立摆模型，可以对已有的控制方法和理论进行模拟和验证，从而提出一些新的理论方法，并将其应用于人工智能、生物工程、计算机视觉、航空航天等领域.目前,对于倒立摆的控制主要包括状态反馈、线性二次型调节器(LQR)等现代控制理论方法，根轨迹、比例-积分-微分(PID)等经典控制理论方法，以及模糊、神经网络、支持向量机等智能方法.其中，PID方法由于理论成熟、便于实现，在倒立摆的控制中应用最为广泛[3-6].尽管如此，PID方法还是存在一些缺陷，如泛化能力差、鲁棒性不高等.除了PID方法，模糊理论也是应用较多的一种方法[7-9].然而，模糊控制方法的适应性较差，当系统参数改变，或出现未知状况时，控制效果明显变差.因此,将两者结合的研究成果也开始出现，但这些研究目前主要集中于一阶或平面倒立摆[10-11].本文将直线二阶倒立摆作为研究对象，将PID控制和模糊控制相结合，设计一种自适应模糊PID控制器.

1二阶倒立摆的数学模型

一个典型的直线二阶倒立摆模型主要由小车、两个摆杆和连接块组成[12-13]，如图1所示.由于多了一级摆杆，其复杂性远高于一阶倒立摆.

图1　直线二阶倒立摆示意图Fig.1　Linear second-order inverted pendulum schematic

首先，根据倒立摆模型的物理学运动规律建立微分方程，即

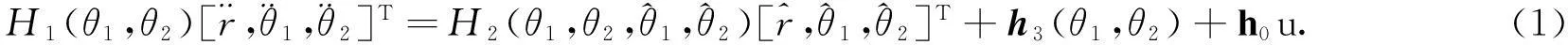
对式(1)在系统平衡点处进行线性化处理，可得系统的状态方程为

2模糊PID控制器设计

2.1　控制器结构

在设计控制器时，考虑将PID算法和模糊算法有机结合，既利用前者的实用性，又结合后者的智能性.根据对二阶倒立摆模型参数和稳定条件的分析，在设计模糊推理时，采用Mamdani的形式，通过在线方式实时调节PID算法的3个参数[13-14].具体思路为：将一个常规PID控制器作为主控制器，另设计一个模糊推理模块，利用该模块对PID控制器的比例、积分和微分3个参数进行自适应整定.

此外，文中进行了两点改进.1) 以往大多数的模糊推理模块只是单纯地将偏差E作为输入,为了更为客观、迅速地反映系统变化，将偏差变化率CE也作为一个输入.2) 设计模糊推理模块的输出为参数的变化调整量，则PID算法只需进行相应的调整即可.这样模糊推理模块就形成了一个2输入、3输出的结构，具体如图2所示.由图2可知：该控制器结构同时具有PID和模糊两种算法的优点，其动态和静态性能较好，非常适合二阶倒立摆这样的非线性动态系统控制.

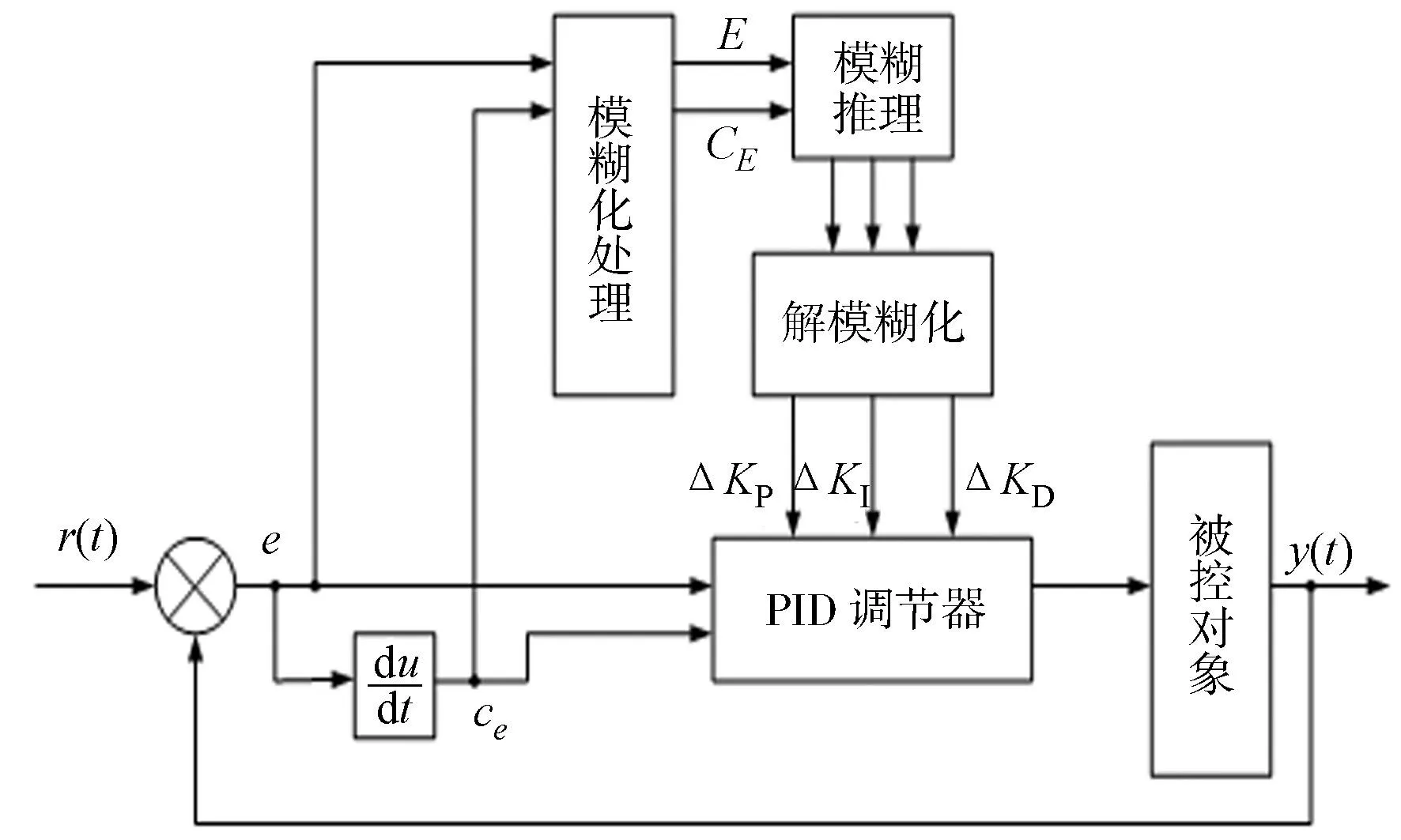
图2　模糊PID控制器结构Fig.2　Structure of the fuzzy PID controller

2.2　控制规则的制定

根据设计的模糊PID控制器的结构，将二阶倒立摆的摆杆1和摆杆2所在的角度偏差E及其变化率CE作为系统输入.设定角度偏差E和偏差变化率CE的模糊子集为{负大，负中，负小，零，正小，正中，正大}，利用符号表示为{NB,NM,NS,Z,PS,PM,PB}，输出模糊子集与其具有相同形式的符号表示.根据E和CE对系统影响程度的不同，当变化超过60%时，即达到了模糊推理模块的最大值，故设定E和CE基本论域分别为[-80，80]，[-10，10]，输入量的模糊论域为[-6，6]；3个输出变量ΔKP，ΔKI和ΔKD的基本论域为[-0.4，0.4]，[-0.06，0.06]，[-3， 3]，模糊论域为[-3，3].考虑到等三角函数的灵敏度较高，可以在论域范围内均匀分布，故将其作为隶属度函数.

据此，对PID算法的比例 KD、积分KI、微分KD等3个参数制定不同情况下的整定规则.

1) 当角度偏差E变化较大时，很可能出现微分过饱现象，使系统超出控制范围.为了保证系统能够快速响应，KP应设定为一个较大数值，KD相应的需设定较小一些，同时取KI，防止系统超调过大.

2) 当角度偏差E和偏差变化率CE的值在适中范围时，既要考虑系统的超调不能过大，又要保证系统具有较快的响应速度，KP需设定一个较小的数值，KI和KD取值适中即可.

3) 当角度偏差E变化较小时，首先,需要让系统维持较好的稳定性，KP和KI都应设定较大的数值；其次，考虑降低系统振荡的风险，KD应与角度偏差变化率CE的取值进行相反设定.

针对比例KP、积分KI、微分KD等3个参数的模糊控制规则，分别如表1～3所示.

表1 KP模糊控制规则表Tab.1 FuzzycontrolruletableofKPECENBNMNSZPSPMPNNBPBPBPMPMPSZZNMPBPBPMPSPSZNSNSPMPMPMPSSNSNSZPMPMPSZNSNMNMPSPSPSZNSNSNMNMPMPSZNSNMNMNMNBPNZZNMNMNMNBNB表2 KI模糊控制规则表Tab.2 FuzzycontrolruletableofKIECENBNMNSZPSPMPNNBNBNBNMNMNSZZNMNBNBNSNSNSZZNSNMNMNSZZPSPSZNMNSZPSPSPMPMPSNSNSPSPSPSPMPBPMZPSPSPMPMPBPBPNZPSPMPMPMPBPB表3 KD模糊控制规则表Tab.3 FuzzycontrolruletableofKDECENBNMNSZPSPMPNNBPSNSNBNBNSNMPSNMPSNSNSNMNSNSZNSZNSNMNMZNSZZZNSNSNSPSNSZPSZZZZPSZZPMPBNSPSPSPSPBPBPNPSPMPMPMPSPBPB

3仿真实验分析

对提出的模糊PID控制器的二阶倒立摆控制性能进行仿真分析，并与文献[4]提出的PID方法进行对比.利用Matlab软件的Simulink模块，搭建PID控制算法的系统，结果如图3所示.这3个PID控制器分别控制小车位移r和两个摆杆的角度α1和α2[15].对于二阶倒立摆这样的典型不稳定系统，初始值的不同对于PID算法的控制效果具有很大的影响，选择不当会使控制品质下降，甚至系统发散.

图3　PID控制仿真结构图Fig.3　PID control simulation chart

选择两组初始参数，分别设定为 (r，α1，α2)={0，0，0}，(r，α1，α2)={-0.1，-0.2，-0.1}，控制效果如图4所示.由图4可知：PID方法对于二阶倒立摆具有一定的控制效果，要求系统初始参数选择适当；第一组参数明显具有更短的调节时间，但第二组参数的超调量更小.此外，PID方法的3个参数也需根据经验或经过多次反复试验给定，泛化性较差.

(a) 第一组　　　　　　　　　　　　　　　　　　(b) 第二组图4　参数的PID仿真结果Fig.4　PID simulation results with the parameters

其次，根据设计的模糊PID控制器搭建系统模型，将图3中的3个常规PID控制器替换为图5所示的模糊PID控制器即可，其他不变.在仿真过程中，仍取上述相同的两组初始条件，仿真结果如图6所示.由图6可知：模糊PID对于二阶倒立摆具有较好的控制效果.相较于常规PID方法，模糊PID降低了系统对于初始值的敏感度，两组参数情况下的控制效果相当，超调量和调节时间都明显较小，且明显好于常规PID方法.

图5　模糊PID控制器仿真模型Fig.5　Simulation model of fuzzy PID controller

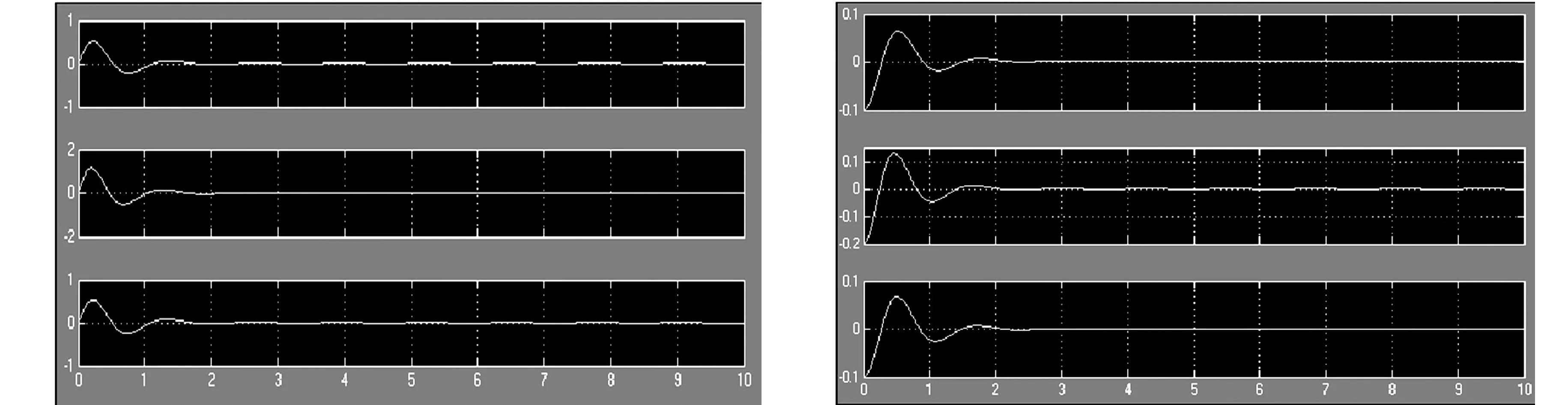
(a) 第一组　　　　　　　　　　　　　　　　　　　　(b) 第二组图6　参数的模糊PID仿真结果Fig.6　Fuzzy PID simulation results with the parametres

最后，在程序编译成功之后，采用手动方式将摆杆提到中间的一个平衡位置，运行程序，其控制效果如图7，8所示.

由图7,8可知:模糊PID方法对于二阶倒立摆系统控制的稳定度明显高于常规PID方法，两个摆杆角度的变化幅度也明显较小.多次改变系统初始参数，控制效果基本相同，这里不一一赘述.

图7　PID控制器的实际控制结果　　　　　　　　图8　模糊PID控制器的实际控制结果Fig.7　Actual control results for PID controller　　Fig.8　Actual control results for fuzzy PID controller

在系统运行过程中，突然施加一个外部扰动，考察模糊PID方法的抗干扰性，控制结果如图9所示.由图9可知：在系统运行第3s时，突然受到一个外部干扰，但是在大概2s以后就迅速恢复为稳定状态，而且系统的超调量较小，说明模糊PID方法对于外部扰动具有较好的抑制作用.

图9　扰动情况下模糊PID控制器的实际控制结果Fig.9　Actual control results for fuzzy PID controller with disturbance

综合比较以上结果可知，所设计的模糊PID控制器对二阶倒立摆具有较好的控制效果，无论是超调量，还是调节时间都明显好于常规PID方法.

4结束语

采用自适应模糊PID对直线二阶倒立摆的控制问题进行研究.首先,建立二阶倒立摆的数学模型，反映出其是一个典型的不稳定系统；其次，将常规PID算法与模糊理论相结合，设计模糊PID控制器，可以实现PID参数的自适应模糊整定[16].仿真及实测实验表明：所设计的模糊PID控制器可以很好地实现二阶倒立摆的扶起平衡控制，控制效果明显好于常规PID控制器，超调量和调节时间较小，并具有较好的抗干扰能力，为直线二阶倒立摆的控制问题提供了一条可借鉴的思路.

参考文献：

[1]赵建军，魏毅，夏时洪,等.基于二阶倒立摆的人体运动合成[J].计算机学报，2014，37(10):2187-2195.

[2]吴震宇，方敏，丁康.基于LabVIEW的二级倒立摆控制系统三维仿真[J].合肥工业大学学报(自然科学版)，2011，34(10):1480-1484.

[3]项雷军，王涛云，郭新华.多区域互联电网的分散式模糊PID负荷频率控制[J].华侨大学学报(自然科学版)，2014，35(2):121-126.

[4]杨平，徐春梅，贺茂康,等.直线二级倒立摆的PID实时控制[J].上海电力学院学报，2008，24(3):236-238.

[5]王宏楠.基于RBF神经网络二级倒立摆系统的PID控制[J].辽宁石油化工大学学报，2010，30(2):58-61.

[6]王俊.基于倒立摆的PID控制算法的研究[J].现代电子技术，2012，35(23):152-154.

[7]李红伟.单级倒立摆的简化模糊控制及仿真研究[J].控制工程，2010，17(6):769-773.

[8]侯涛，牛宏侠.平面一级倒立摆的双闭环模糊控制研究[J].兰州交通大学学报，2011，30(4):11-19.

[9]侯涛，范多旺，杨剑锋.基于T-S型的平面倒立摆双闭环模糊控制研究[J].控制工程，2012，19(5):753-756.

[10]王子涛，王家军，何杰.基于自适应模糊PID平面倒立摆的建模与仿真[J].杭州电子科技大学学报，2010，30(4):86-91.

[11]杨治明，宋乐鹏，杨清林,等.基于模糊控制和PID控制的一阶倒立摆系统建模与仿真[J].北华大学学报(自然科学版)，2012，13(3):356-359.

[12]洪江，周明华.二阶倒立摆的稳定性控制[J].科技资讯，2012，36(27)：70-71.

[13]王春民，栾卉，杨红应.倒立摆控制的设计与仿真[J].吉林大学学报(信息科学版)，2009，6(3)：242-247.

[14]王广雄，张静，罗晶，等.倒立摆的模型和控制问题[J].电机与控制学报，2004，8(3)：247,262-295.

[15]柴军营，何广平.倒立摆的一种新的控制方法[J].北方工业大学学报，2007，4(3)：26-30.

[16]李贤涛，张葆，赵春蕾，等.基于自适应的自抗扰控制技术提高扰动隔离度[J].吉林大学学报(工学版)，2015，6(1)：202-208.

(责任编辑： 钱筠英文审校： 吴逢铁)

ResearchonDoubleInvertedPendulumControl

UsingAdaptiveFuzzyPID

SONGGuojie

(CollegeofElectronicEngineering，SipingVocationalCollege，Siping136002，China)

Abstract：In this paper, a mathematical model of second-order inverted pendulumis built. The conventional proportional-integral-differential (PID) control and fuzzy controlare combined, and a fuzzy PID controlleris designed. The adaptive fuzzy tuning of PID parameters is obtained. Simulation results show the designed fuzzy PID controller can well realize the propped balance control of second-order inverted pendulum, the control effect is obviously better than the conventional PID controller, the overshoot and adjust time is small, and has a good anti-jamming capability. It is very suitable for the stability control of the model of second-order inverted pendulum.

Keywords：inverted pendulum; fuzzy control; proportional-integral-differentia controller; adaptive; stability control

基金项目：吉林省教育厅“十一五”科学技术研究项目(2012年度)

通信作者：宋国杰(1978-)，女，副教授，主要从事电子技术、可编程逻辑控制器和自动控制的研究.E-mail:songguojie530@sina.com.

收稿日期：2015-11-13

中图分类号：TP 391.9

文献标志码：A

doi:10.11830/ISSN.1000-5013.2016.01.0074

文章编号：1000-5013(2016)01-0074-05