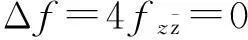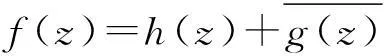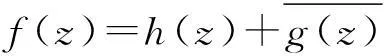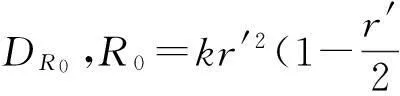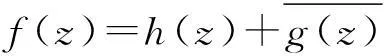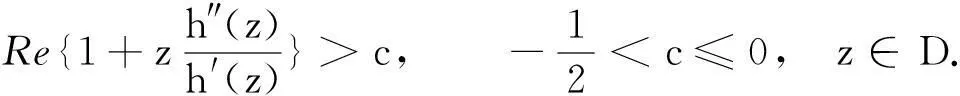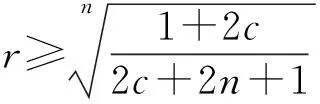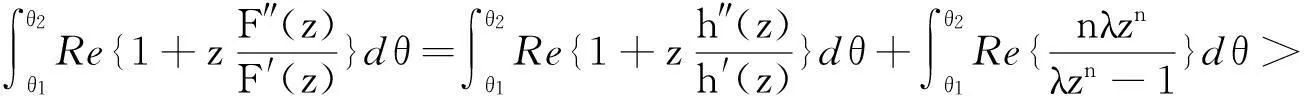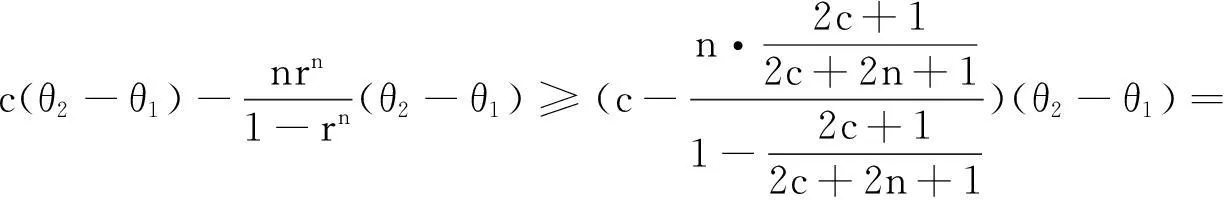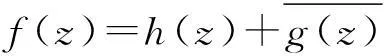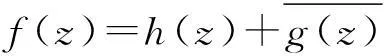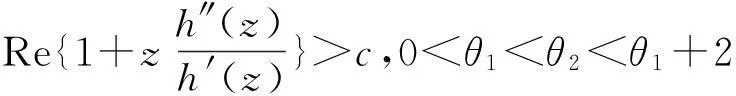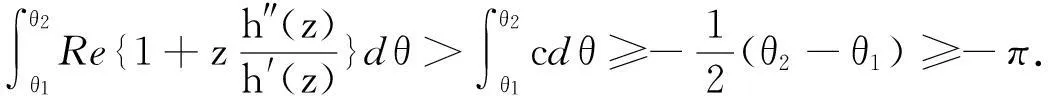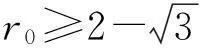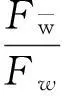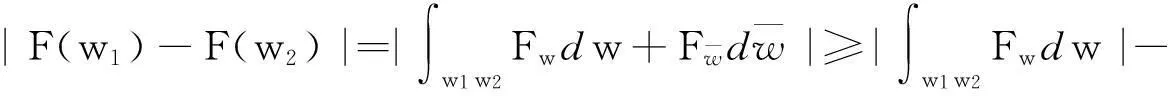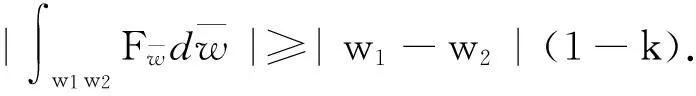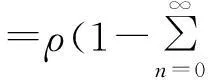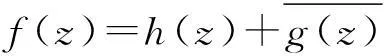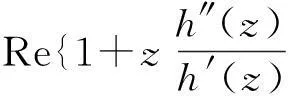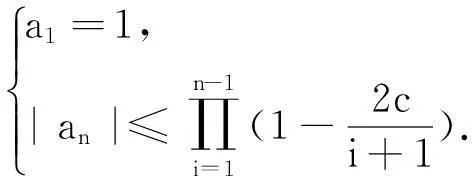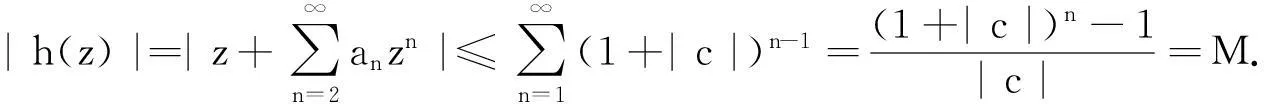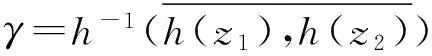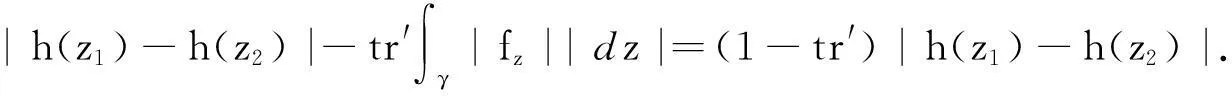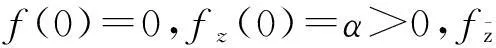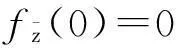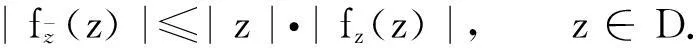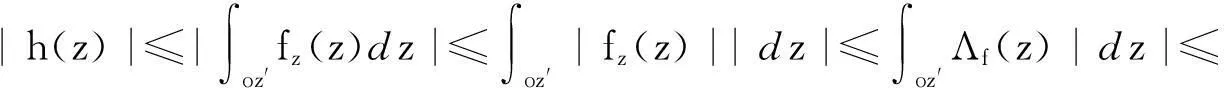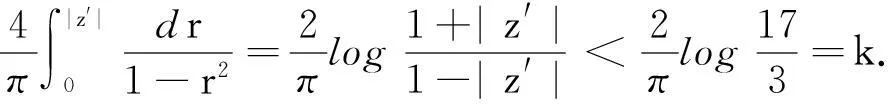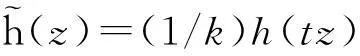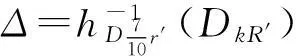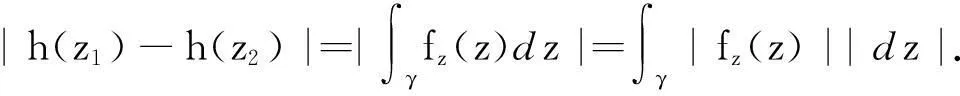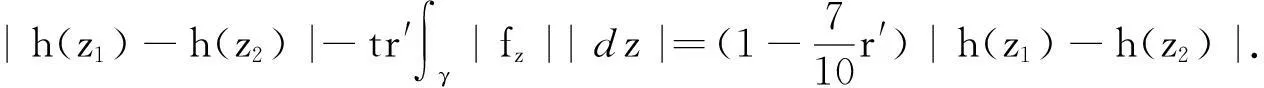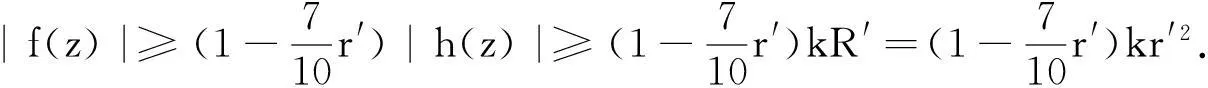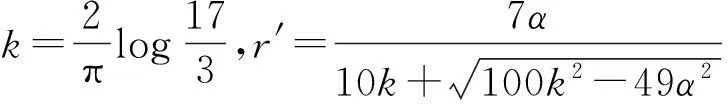某类调和函数的单叶半径和Landau定理

黄心中, 黄赟

(华侨大学 数学科学学院, 福建 泉州 362021)



某类调和函数的单叶半径和Landau定理

黄心中, 黄赟

(华侨大学 数学科学学院, 福建 泉州 362021)

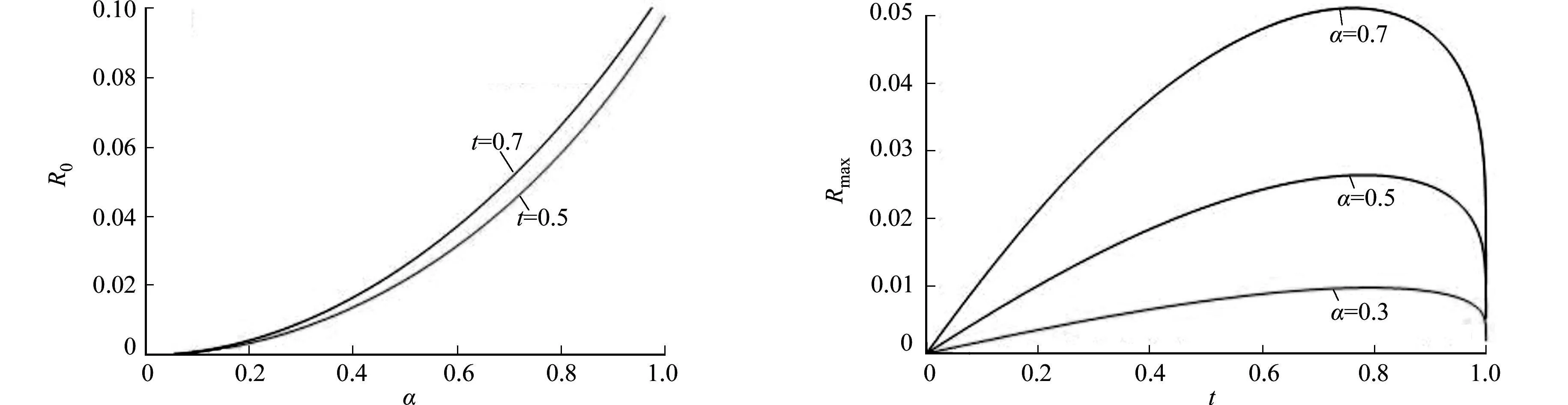
摘要：研究单位圆盘D上解析部分h(z)满足

关键词：调和函数； 稳定近于凸； 单叶半径； Landau定理

1预备知识

调和函数稳定近于凸性质和单叶半径的研究受到许多学者的关注,且有不少进展[5-7].文中对复伸张w(z)=zn时，利用解析函数近于凸判定定理和稳定近于凸的充要条件,对f(z)的稳定近于凸半径做出估计;当|w(z)|<1时,利用单叶解析函数的凸半径估计，进而估计f(z)的单叶半径.

Landau定理和Bloch常数是复分析理论中的重要课题,近年来人们在函数类间建立联系,试图利用解析函数的Landau定理推广到调和函数的情形[8-10].

Chen等[8]利用调和函数解析部分的性质和Schwarz引理,得到了调和函数的Landau定理D.

利用定理B中的系数估计,给出满足其条件的函数类的Landau定理,同时对定理D的证明过程进行改进,得到了更佳的结果.

2主要结果及证明

将定理A进一步推广到复伸张为w(z)=zn的情形,得到定理1.

证明考虑解析函数F(z)=h(z)-λg(z),其中|λ|=1,那么

其中，θ1<θ2<θ1+2π.

解析部分满足相同条件的情况下,复伸张w(z)为n次多项式时,可以由定理2得到调和函数f(z)的单叶半径估计.

则F(w)在h(Dρ)上单叶,又h(z)在Dρ上单叶，所以f(z)在Dρ上单叶.

在定理B中得到了解析部分的系数估计表达式,利用这一表达式,对该函数类的Landau定理进行描述.

因此,

令z1→∂Dtr′,z2→0,有|f(z)|≥(1-tr′)|h(z)|≥(1-tr′)MR′=(1-tr′)Mr′2.

当|z′|

因此,

令z1→∂Dtr′,z2→0,有

这一结果改进了文献[8]的定理3.在t=0.7和t=0.5的情况下，单叶区域在满足条件的f作用下,覆盖圆的最大半径R0的变化,如图1所示.R0的取值随着调和函数f的解析部分h(z)的一次项系数α的取值而变化，如图2所示.

由图2可知：当α=1时,单叶区域在f作用下的值域覆盖的圆半径达到最大,约为0.106.

图1　R0随t变化曲线 图2　R0随α变化曲线Fig.1　Curves of R0 with different values of t　　　　　Fig.2　Curves of R0 with different values of α

参考文献：

[1]BSHOUTYD,LYZZAIKA.Close-to-convexitycriteriaforplanarharmonicmappings[J].ComplexAnalysisandOperatorTheory,2011,5(3):767-774.

[2]MOCANUPT.Injectivityconditionsinthecomplexplane[J].ComplexAnalOperTheory,2011,5(3):759-766.

[3]BSHOUTYD,LYZZAIKA.Problemsandconjecturesinplanarharmonicmappings[J].JAnalysis,2010,18:69-81.

[4]黄赟,黄心中.某些近于凸调和函数的解析性质和系数估计[J].华侨大学学报(自然科学版),2015,36(4):478-483.

[5]HERNNDEZR,MARTNMT.Stablegeometricpropertiesofanalyticandharmonicfunctions[J].MathProcCambPhilSoc,2013,155(2):343-359.

[6]石擎天,黄心中.调和映照与其剪切函数的单叶性[J].华侨大学学报(自然科学版),2013,34(3):334-338.

[7]王其文,黄心中.在微分算子作用下调和函数的单叶半径估计[J].华侨大学学报(自然科学版),2014,35(2):227-231.

[8]CHENHuaihui,GAUTHIERPM.Thelandautheoremandblochtheoremforplanarharmonicandpluriharmonicmappings[J].ProceedingoftheAmericanMathematicalSociety,2011,139(2):583-595.

[9]李东征，陈行堤.调和函数的Landau定理[J].华侨大学学报(自然科学版),2012,33(5):584-289.

[10]李东征，陈行堤.调和函数的Bloch定理[J].华侨大学学报(自然科学版),2012,33(1):103-106.

OntheUnivalentRadiusandLandauTheorem

(责任编辑： 黄晓楠 英文审校： 黄心中)

forSomeHarmonicMappings

HUANGXinzhong,HUANGYun

(SchoolofMathematicalSciences,HuaqiaoUniversity,Quanzhou362021,China)

Keywords：harmonic mapping; stable close-to-convex; univalent radius; Landau theorem

基金项目：国家自然科学基金资助项目(11471128); 福建省自然科学基金资助项目(2014J01013)

通信作者：黄心中(1957-)，男，教授，博士，主要从事函数论的研究.E-mail:huangxz@hqu.edu.cn.

收稿日期：2015-08-23

中图分类号：O 174.51； O 174.55

文献标志码：A

doi:10.11830/ISSN.1000-5013.2016.01.0120

文章编号：1000-5013(2016)01-0120-05