Bandelet变换及其逼近特性分析

黄永

(昭通学院 数学与统计学院， 云南 昭通 657000)



Bandelet变换及其逼近特性分析

黄永

(昭通学院 数学与统计学院， 云南 昭通 657000)

摘要：首先，从几何流和地平线模型出发，分析流积分及其扫描带内的边缘表达；其次，抑制离散二元小波基函数的不足，构建Bandelet变换的标准正交基；最后，对Bandelet变换在扫描带内的逼近特性进行分析，构建估计边缘和真实边缘的逼近误差计算公式.结果表明：文中方法在图像边缘表达上可以得到最优框架.

关键词：Bandelet变换； 基函数； 逼近特性； 估计边缘

Bandelet变换经历了两代变换理论的发展，其主要应用领域都是图像稀疏表达和图像压缩[1-4].其中，Pennec对于第一代Bandelet变换做出了重要贡献，他不仅参与提出第一代Bandelet变换理论，还进一步对Bandelet变换进行完善和发展，大大提升其在实际中的应用性[5].Bandelet变换的最大优势在于，它弥补了小波变换各向异性特征表达的缺陷，更利于图像的稀疏表达和稀疏编码[6].第一代Bandelet变换技术是建立在小波变换的理论之上，从连续到离散进行推理和演进，进而依托几何流概念构建Bandelet变换基函数，从而推动离散Bandelet变换算法、连续Bandelet变换算法、快速Bandelet变换算法的发展[7-10].本文从Bandelet变换原理出发，进而对Bandelet变换的带内逼近特性、全局逼近特性展开分析.

1Bandelet变换的基本原理

Bandelet变换是以处理图像压缩、图像编码、图像稀疏表达为出发点建立的.

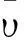
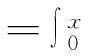
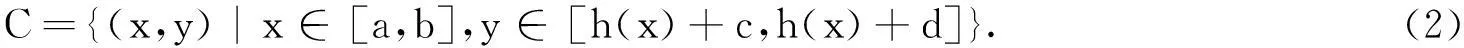
对g(x，y)作一个变换，即x=u，y=v+g(u)，分析Bandelet变换基函数的构建.用θ(t)表示一维的小波函数，用ϑ(t)表示这个小波函数对应的尺度函数，分别记为

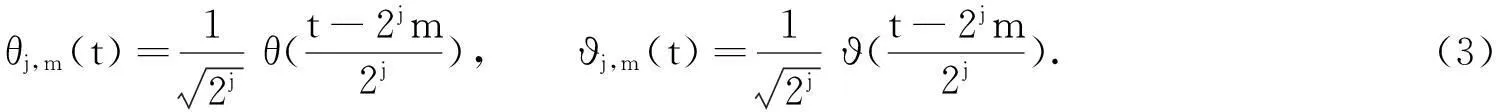
由此构建二元小波基函数为

通过反解，可以获得带状区域C上的标准正交基，即

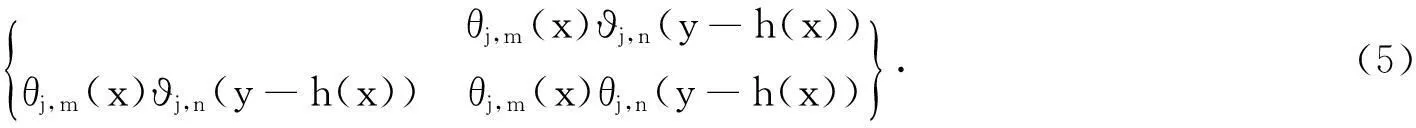
2Bandelet变换的带内逼近特性分析

假设J(x，y)表示一个模糊核，对这个模糊核执行伸缩变换处理，其数学形式为

J1在集合[-1，1]2上得到支撑，则同时存在

模糊核J(x，y)可以对图像边缘施加处理，这个处理的范围呈现为一个带状区域，用Ar表示.Ar区域内的点到达边缘的距离E符合如下关系，即

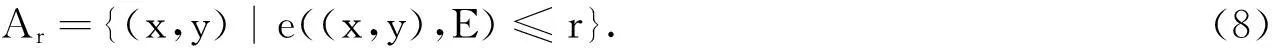
针对Bandelet变换在Ar区域内的逼近特性展开分析.

Bandelet变换的原理始于几何流，相应的基函数的构造也出于同源.因此，分析Bandelet变换的带内逼近特性，需要从几何流的逼近特性开始.对于几何流的逼近效果而言，要使其达到最佳，必须尽可能地减少控制参量的个数[11].

假设Ar可以在x轴上获得投影，且投影区间位于[a，b]，可以计算出区间长度为d1=b-a.基于此，对于几何流的逼近，可以使用尺度2k下的一族正交函数，如{fk，m(t)|d≤m≤d12-k}.在这簇正交函数中，支撑集合包含在[a，b]内的函数可以用f(2-kt-m)描述，满足

如果{fk，m(t)|d≤m≤d12-k}的空间Wk中含有q阶次的多项式，则f(t)是紧支撑q阶次的可微函数.基于此，式(9)中的h(t)受控于尺度大小2k和(b-a)2-k个系数{βm}.又因为|h′(x)|≤2，忽略常数的影响，再做一假设h(a)=0，存在|h(x)|≤2d1，且存在一个常数Cf，这个常数仅和尺度函数f(t)存在关联，且这个常数使不等式|βm|≤Cf(b-a)成立.

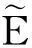
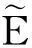
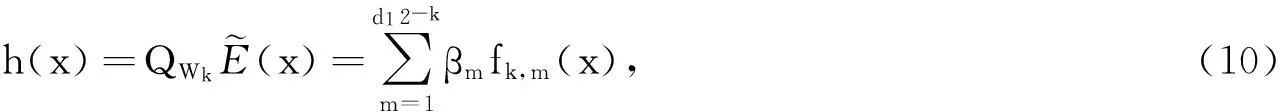
式(10)，(11)中：参数CE和尺度2k如果小到一定程度，流线积分h(x)和边缘的精确特征E(x)之间的误差就会控制地非常小.

正是因为流积分的存在，才能根据一维小波函数θ(t)构造Bandelet变换的基函数.为了简化Bandelet变换基函数的表达，将θj，m(x)θj，n(y-h(x))用{cm}替代.那么，可以描述Bandelet变换基函数对几何图像g的稀疏的表达式为

至此，根据Bandelet变换对图像的稀疏表达可知，整个表达需要N=Nh+Nc个参数.其中：Nh表示流积分所用的参数；Nc表示实现图像逼近所需的参数.

最后，对Bandelet变换的逼近能力，给出如下结论.

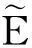
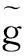
除了得到Bandelet变换逼近特性的确定性误差计算公式外，还可以得到一个结论：对于β阶次地平线模型，Bandelet变换在一个Bandelet带内，可以达到最佳的逼近特性.

3Bandelet逼近特性在图像分割中的应用

3.1　Bandelet正交基框架

Bandelet变换起源于对图像信息的压缩编码等处理，进而又可以进一步为图像处理技术服务，在图像分割方面有比较理想的应用效果[12].

在Bandelet变换理论中，Bandelet变换正是由图像中各个边缘特征附带的几何流思想引申出来的.这些边缘特征信息附带的几何流，可以被用于自适应地跟踪图像之中可能存在的几何正则方向.正常情况下，几何流信息和图像边缘特征的走向是保持一致的.图像中边缘特征，如果放大到局部的任意一个点上，可以被区分为两种情况：沿着水平方向排布的边缘;沿着垂直方向排布的边缘.

根据这样的边缘特征可能排布方向，图像在二进制表达的过程中，图像的全部区域Θ可以形成一个细分的结果，其数学形式为Θ∪Θi.其中：Θi表征每一个被细分的图像区域.这种细分工作做到非常细致的程度时，每一个Θi内最多只保留一条边缘特征线.图像的分割情况，如图1所示.图1中：黑色的粗线为图像中的边缘特征；虚线框为分割出的区域.最终分割出的区域可分为如下4种主要类型：

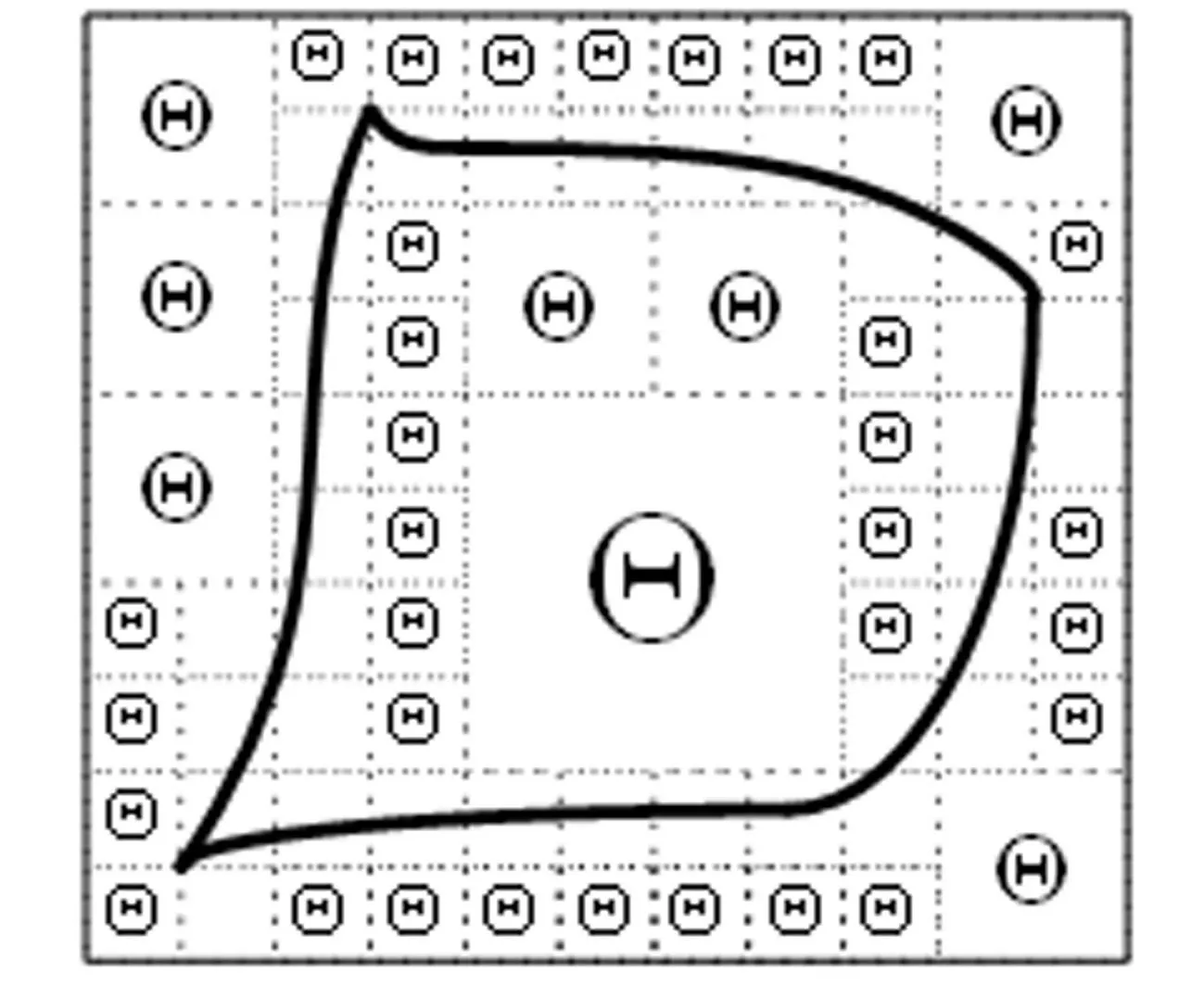
图1　图像的分割Fig.1　Image segmentation

1) 区域内含有边缘特征信息，且边缘特征的方向是水平的；

2) 区域内含有边缘特征信息，且边缘特征的方向是垂直的；

3) 区域内含有边缘特征信息，恰好是两个方向走势的边缘特征不同走向，并形成相交；

4) 区域内不含有任何边缘特征信息.

进一步定义一个正交投影的计算子，其数学表达形式为

式(14)中:QΛg(x，y)为这个正交投影的计算子；Λ为正交投影计算子的空间.

进一步可以得出，在图像分割形成后的每一个区域上的正交投影计算子，可以合并成L2([0，1]2)上的一个完整的框架，这个框架就是Bandelet正交基框架.

3.2　Bandelet字典和分割寻优

实际上，构建Bandelet框架的意义在于，将要分析的图像按照支撑空间划分成细小的区域.这样每一个细小的区域上可以采用几何流特征执行Bandelet逼近处理或者小波逼近处理.这个分割处理的过程相当于执行二进制分割的策略.首先，第一个层次上图像被划分成完全相等的4个小子块图像，可以采用四叉树的方法对这个分割结果进行表示.然后，每一个子块的图像又可以根据是否含有特征信息的具体情况进一步执行二进制细分处理.

采用一个具体的图形说明这一分割过程，如图2所示.由图2可知：原始图像已经被划分为多个子块图像，分别是子块图像A，B，C，D，E，F，G，H，I，J，K，L，M.这是一个多次二进制分割的结果，原始图像经过三级分割，子块图像M，L属于第一级分割结果；左上角第一层级分割图像又被分为4个子块图像，即子块图像E，F，G，H；右下角第一层级分割图像又被分成4个子块图像，即子块图像I，J，K，以及最右下角的子块图像，它又被进一步细分成4个三级子块图像，即子块图像A，B，C，D.

根据Bandelet变换构建的原始图像四叉树表达，如图3所示.由图3可知：子块图像L，M成为第二级四叉树节点；子块图像E，F，G，H，I，J，K成为第三级四叉树节点；子块图像A，B，C，D成为第四级四叉树节点.当然，子块图像L，M，E，F，G，H，I，J，K，A，B，C，D也都最终成为叶子节点.

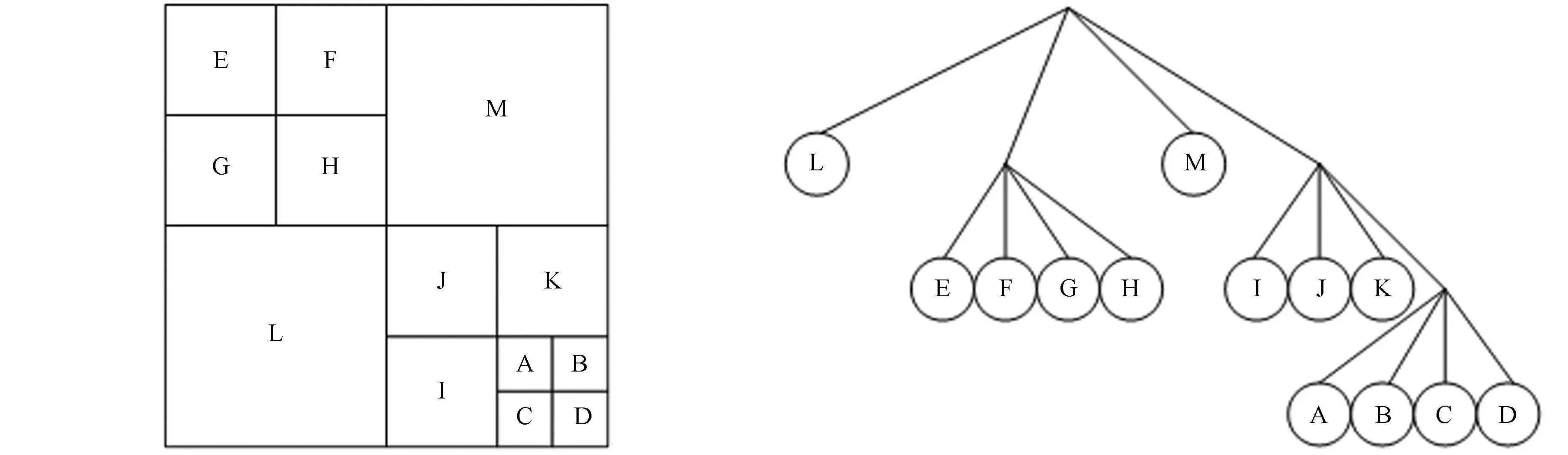
图2　基于Bandelet变换的图像二进制分割处理　　　　　图3　基于Bandelet变换的图像四叉树构建　　Fig.2　Binary image segmentation based on Fig.3　Image 4-fork tree construction based on 　Bandelet tranform　　　　　　　　　　　　　　　　　Bandelet tranform

图2所示的图像分块结果和图3所示的四叉树结果是一一对应的.如果将原始图像的整体宽度设置为1时，则对应宽度为2-k的图像子块相当于在Bandelet四叉树中具有的节点深度为|k|.

在图1中：每一个用Θi标记的小图像方块，都可以采用一个参量表达这个小图像方块上的基函数是小波基函数，还是Bandelet基函数.如果其中的基函数是Bandelet基函数的类型，还需要进一步对Bandelet基函数构建模型的类别进行区分，即区分是水平方向上的基函数构建模型，还是垂直方向上的基函数的构建模型.

如前文所述，因为基函数模型需要借助流积分进行构造，因此，需要对在尺度2ki之下的流积分进一步明确表达，即

原始图像分割后形成的所有子块图像，其上的Bandelet基函数或小波基函数所构建的完整集合，可以形成一个可用于Bandelet分析的逼近框架.即

式(16)中:F为一个子块图像上Bandelet基函数构成的框架；B为这个子块图像上的Bandelet基函数；FC为全部子块图像形成的逼近框架，C为框架中所含有的全部参数的个数，C=CS+CH+CB，CS为原始图像二进制分割所需要的参量个数，CH为原始图像几何流表达所需要的参量个数，CB为原始图像Bandelet表达所需要的参量个数.

至此，要获得图像分割最优结果的过程，就变成对式(16)的框架进行寻优的过程.如果原始图像的分辨率可以限制在T2之内，按照Lagrange方法对C计算式执行寻优过程，那么，原始图像四叉树的最大深度可以表示为‖|log2T2|-1‖.此时，如果将流积分参数βn执行量化处理，则对于尺寸为2k的子图像块而言，在|βn|

4结束语

对Bandelet变换的基本原理及逼近特性展开研究.依托几何流和地平线模型分析Bandelet变换的基础流积分,在二元小波变换的理论基础之上，构建Bandelet变换的标准正交基.对Bandelet变换逼近特性进行分析，并利用这种性质实现图像边缘逼近的Bandelet最优框架.

参考文献：

[1]SHANTHII，VALARMATHIML.SARimagedespecklingusingpossibilisticfuzzyC-meansclusteringandedgedetectioninbandeletdomain[J].NeuralComputingandApplications，2013，23(1):279-291.

[2]杨杨，戴明，周箩鱼，等.基于非下采样Bandelet变换的多聚焦图像融合[J].吉林大学学报(工学版)，2014，44(2):525-530.

[3]PANDIANK，SOUNDARAK，KUMARE，etal.ReconstructionofmissingdatainVHRimagesusingBandeletandexemplarbasedinpaintingstrategies[C]∥3rdInternationalConferenceonComputerTechnologyandDevelopment.Chengdu：[s.n.]，2011：25-27.

[4]MAALOUFA,LARABIMC.Bandeletbasedstereoimagecoding[C]∥InternationalConferenceofAcoustics，Speech，andSignalProcessing.Dallas:IEEEPress,2010:698-701.

[5]MAALOUFA,LARABIMC.ImageretargetingusingaBandelet-basedsimilaritymeasure[C]∥InternationalConferenceonAcoustics，Speech，andSignalProcessing.Dallas:IEEEPress,2010:942-945.

[6]JANSENM，CHOIH，LAVUS，etal.Multiscaleimageprocessingusingnormaltriangulatedmeshes[C]∥InternationalConferenceonImageProcessing.Thessaloniki:IEEEPress,2001:229-232.

[7]WAKINM，ROMBERGJ，CHOIH，etal.Ratedistortionoptimizedimagecompressionusingwedgelets[C]∥InternationalConfernceonImageProcessing.Newyork:IEEEPress，2002:237-240.

[8]CANDESE，DONOHOD.NewtightframesofcurveletsandoptimalrepresentationsofobjectswithpiecewiseC2singularities[J].PureApplicationofMath，2004，57(4):219-266.

[9]潘晓明，余俊，杨钊，等.一种将线性粘弹微分型本构方程应用到ABAQUS的方法[J].华侨大学学报(自然科学版)，2010，31(5):570-575.

[10]ARTEAGAJA，VELASCOMJ.DesignofimagecodecbasedonBandelettransformusingaNIOSⅡprocessor[J].IngeniareRevistaChilenaDeIngenieria，2012，20(2):211-219.

[11]綦科,谢冬青.基于第二代Bandelet变换的抗几何攻击图像水印[J].自动化学报,2012,38(10):1646-1653.

[12]刘绪崇,罗永,王建新,等.基于第二代Bandelet变换的图像认证水印算法[J].通信学报,2010,31(12):123-129.

(责任编辑： 钱筠英文审校： 吴逢铁)

BandeletTransformandAnalysisofItsApproximationCharacteristics

HUANGYong

(CollegeofMathematicsandStatistics，ZhaotongUniversity，Zhaotong657000，China)

Abstract：Firstly, the flow integral and the edge expression in the scanning band are analyzed from the geometric flow and the horizon model. Secondly, the standard orthogonal basis of Bandelet transform is built by considering the problem of the suppression for the discrete wavelet basis functions. Finally, we analyze the approximation property of the Bandelet transform in the scanning band, and construct the approximate error figure for the estimating edge and the real edge. Results show that the optimal frame can be obtained by the image edge expression.

Keywords：Bandelet transform； basis function； approximation property； estimated edge

基金项目：云南省教育厅科学研究基金资助项目(2014Y499)

通信作者：黄永(1966-)，女，副教授，主要从事Bandelet变换逼近特性的研究.E-mail:3281578930@qq.com.

收稿日期：2015-11-13

中图分类号：TN 919.81

文献标志码：A

doi:10.11830/ISSN.1000-5013.2016.01.0062

文章编号：1000-5013(2016)01-0062-05