三维混沌映射和位信息处理的图像隐藏算法

李冰立

(衡水学院 数学与计算机学院， 河北 衡水 053000)



三维混沌映射和位信息处理的图像隐藏算法

李冰立

(衡水学院 数学与计算机学院， 河北 衡水 053000)

摘要：构建一种基于三维混沌映射和位信息交换处理相结合的图像隐藏方法，将原始图像的高低Bit位进行交换，进而和Qi映射形成的3个维度上混沌序列截断矩阵进行异或处理，完成图像信息隐藏.实验结果表明：所提出的方法具有良好的视觉隐藏效果，隐藏后的图像在3个方向上的相关性非常低，并且对微小的密钥变化也非常敏感.

关键词：图像隐藏； 位信息； Qi混沌映射； 三向相关性

所谓图像隐藏技术，就是将明文图像进行置乱等保护性操作以形成密文图像，密文图像上无法看到明文图像的准确信息表达，从而达到图像信息隐藏、图像信息加密的目的[1-3].在图像信息技术发展的早期阶段，基于密码流理论和矩阵变换理论的方法很多，先后出现了AES加密方法、DES加密方法、Arnold矩阵加密方法、Barker矩阵加密方法[4-5].但是，这些加密方法因为加密理论已经广为人知，加上置乱过程过于简单，非常容易被攻击者破译[6].目前，大量的经典混沌系统和新提出的混沌映射如Loronz混沌映射、Logistic混沌映射、Tent混沌映射等,被应用于图像信息隐藏之中[7-17].混沌理论可以表征确定系统的随机结果，符合图像信息隐藏的基本要求，其遍历轨迹存在非简单重复性，进一步增强了图像隐藏的效果;此外，混沌系统对于初始设定值非常敏感，可以有效地提升图像隐藏过程中的密钥设置安全性.本文结合三维混沌映射及数字图像的位信息操作理论，构建一种新的图像信息隐藏方法.

1新图像隐藏算法的实现流程

选定一个三维混沌映射作为隐藏算法执行的基础，这个三维混沌映射被称为Qi映射，其表达式为

式(1)中：a，b，c为混沌系统的控制参数，整个Qi映射中共有5个平衡点.文中选取a=35，b=8/3，c=80时的混沌状态.

从3个维度上设置图像隐藏后续操作所需的矩阵，则有

式(2)中:X，Y，Z分别代表对Qi混沌系统中x，y，z三个维度数据处理的结果；xn，yn，zn代表了3个维度上第n个数据；xmax，ymax，zmax分别代表截取混沌序列中x，y,z维度上的最大值;xmin，ymin，zmin分别代表截取混沌序列中x，y,z维度上的最小值；mod代表取模的运算.

按照式(2)的方法，从混沌序列中截取和要处理图像的像素数目相等的数据序列，并将其映射成矩阵的形式.假设要处理图像的宽度和高度分别用W，H表示，则从数据序列映射成矩阵的数学式为

式(3)中:Xn表示从Qi映射x维度上截取的原始图像像素总数相等的数据序列，文中从混沌序列中第1 000个数据开始截取，因要处理的图像大小为256 px×256 px，则在x维度上截取的总长度为1 000+256×256;其他两个维度上的处理方法相同，Yn,Zn则分别表示了从Qi映射y，z两个维度上截取的原始图像像素总数相等的数据序列.XW×H，YW×H，ZW×H表示将Xn,Yn,Zn分别映射为矩阵的结果，即按照先行后列排布而成的结果.

对原始图像M0中每一个像素的二进制表达执行位交换处理，得到新的图像M1，其数学过程为

式(4)中:Bit8表达原始图像中每个像素的二进制表达的第8个二进制位，其他类似.

根据图像位信息交换理论，只要将高位图像和低位图像做一个简单的交换，原始图像的内容信息、特征信息就可以被有效地隐藏起来；而在图像解密一端，只要再做一个逆交换，就又可以恢复出原始的图像信息.由此可知，经过高位和低位的交换，原始图像信息将会被很好地隐藏起来.

为了增强隐藏过程的可靠性，用X1和混沌序列截取矩阵XW×H,YW×H,ZW×H进一步执行异或运算，则有

2实验结果与分析

2.1　实验部分

从隐藏效果分析、相关性分析、密钥敏感性分析等角度，验证计算机位信息处理在文中图像隐藏算法中的有效性.实验所用的计算机为Dell笔记本电脑，2.80 GHz的CPU主频，包含两个处理单元，内存大小为8 GB；实验所用的软件配置为Windows 7操作系统，Matlab程序语言设计平台.

2.2　隐藏效果分析

选择一个灰度图像作为实验对象，经过位信息交换处理和混沌矩阵运算处理后，获得的隐藏结果对比图,如图1所示.

(a) 原始图像 (b) 隐藏图像图1　图像隐藏效果对比Fig.1　Image hiding effect contrast

由图1可知：隐藏图像中已经看不到与原始图像内容(包括纹理、细节等特征)相关的情况，隐藏图像呈现出均匀的置乱分布，达到了比较理想的隐藏效果.此外，所构建的图像隐藏算法，在执行时间上也具有较大的优势，因为只涉及到位信息交换处理和矩阵运算，这对这个256 px×256 px灰度图像的隐藏过程，仅仅耗时12 ms.这个直观的视觉隐藏效果测试实验显示，所设计的基于计算机位信息处理和Qi混沌映射结合的方法不仅具有均匀的置乱效果，而且执行速度也非常快.

2.3　相关性分析

相关性分析是考察图像隐藏算法的重要手段之一.相关性分析一般从3个方向上展开，即水平方向上的相关性、垂直方向上的相关性、对角线方向上的相关性.对于原始图像而言，因为图像内容的展现或表达，图像中各个方向上的像素都会存在邻域关联性，或者是分段的关联性.但是，当图像信息被隐藏置乱后，这种相关性就不应该存在了，相关性越低证明置乱效果越好,隐藏性能越佳.

相关性分析的数学实现一般要分为3个环节，即计算图像加密前和图像加密后的像素差异值对比，进而衡量水平方向上的相关性和垂直方向上的相关性.最终，图像加密方法相关性的检验可以归结为

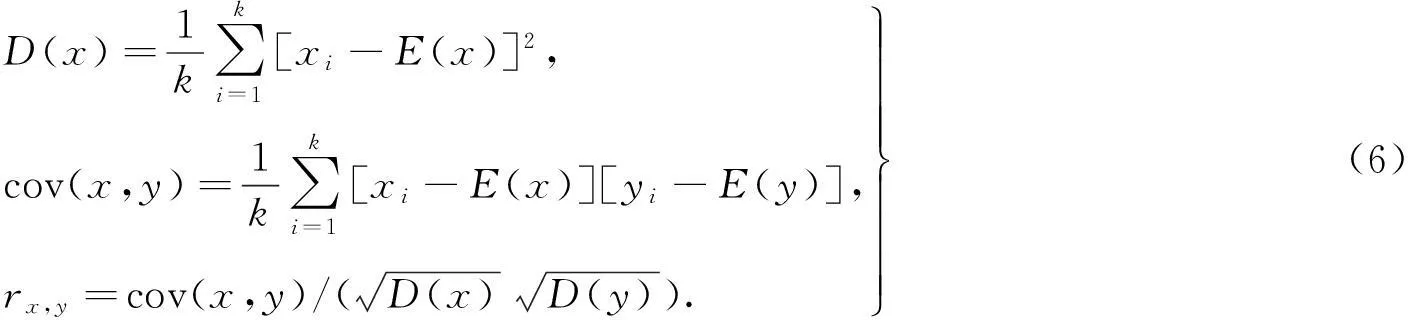
式中:x和y用于表达要加密图像的各个像素灰度值;k是用于表达图像中所含有的像素总个数;E(x)用于表达像素x的数学期望;D(x)用于表达像素x的数学方差;cov(x，y)用于表达像素x和y的协方

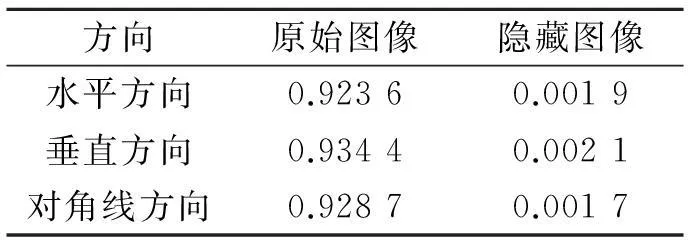
表1　图像的相关性分析

差;rx,y用于表达相关系数.针对图1中原始图像和隐藏图像进行相关性分析，结果如表1所示.由表1可知：原始图像在水平、垂直、对角线方向上的相关程度都非常大，隐藏图像在水平、垂直、对角线方向上的相关程度则非常小.这充分说明隐藏后的图像置乱程度好，关联程度低.

2.4　密钥敏感性分析

密钥敏感性分析也是检测图像隐藏效果非常重要的指标.密钥是解密图像加密算法的重要参数，只有密钥匹配才能破译或解密加密图像.当然，如果解密密钥和真正密钥相差不多，也能获取相当程度的原始图像信息，就证明这种图像加密方法是不理想的.如果密钥有微小变化都不能准确解密，则证明加密方法是对密钥敏感的.文中使用Qi混沌映射的截断序列进行置乱.对于混沌隐藏方法，只有混沌控制参数正确，才有可能准确解密.即便控制参数有微小不符合，也会导致无法准确解密，对于这种性能的检查，就是密钥敏感性分析.

当三个控制参数的值分别是a=35，b=8/3，c=80.01的情况下，考察方法的图像解密效果，如图2所示.由图2可知：虽然3个参数中只有c值有微小的变化，仍然无法准确地解密隐藏图像，这充分说明了所提出方法具有良好的可靠性.

(a) 隐藏图像 (b) 密钥微小差异的解密结果图2　密钥敏感性分析结果Fig.2　Key sensitivity analysis results

3结束语

将计算机位信息处理技术应用于图像隐藏方法的设计之中，通过每一个像素高Bit位和低Bit位之间的交换，可以达到理想的隐藏效果.在此基础上，将整个图像隐藏过程和Qi三维混沌映射结合在一起，利用Qi映射在3个维度上的截断序列映射成矩阵完成三步异或运算.实验结果表明：所提出的方法可以获得均匀置乱的视觉隐藏效果，并且顺利通过了三向相关性检验和密钥敏感性检验.

参考文献：

[1]AZOUG S E，BOUGUEZEL S.A non-linear preprocessing for opto-digital image encryption using multiple-parameter discrete fractional Fourier transform[J].Ptics Communications，2016，359:85-94.

[2]李良，李建军，李钊,等.基于数字图像网络传输的混沌加密算法研究[J].无线电工程，2015，45(10):74-76.

[3]VAFERI E，SABBAGHI-NADOOSHAN R.A new encryption algorithm for color images based on total chaotic shuffling scheme[J].Optik-International Journal for Light and Electron Optics，2015，126(20):2474-2480.

[4]徐亚，张绍武.基于Arnold映射的分块双层自适应扩散图像加密算法[J].中国图象图形学报，2015，20(6):740-748.

[5]ELDOKANY I，EI-RABAIE E S M，ELAHALAFAWY S M,et al.Efficient transmission of encrypted images with OFDM in the presence of carrier frequency offset[J].Wireless Personal Communications，2015，84(1):475-521.

[6]AHMAD J，HWANG S O，ALI A.An experimental comparison of chaotic and non-chaotic image encryption schemes[J].Wireless Personal Communications，2015，84(2):901-918.

[7]郭毅，邵利平，杨璐.基于约瑟夫和Henon映射的比特位图像加密算法[J].计算机应用研究，2015，32(4):1-8.

[8]徐光宪，郭晓娟.基于混沌系统和DNA序列运算的新型图像加密[J].计算机应用研究，2015，32(4):11-15.

[9]张永红，张博.基于Logistic混沌系统的图像加密算法研究[J].计算机应用研究，2015，32(6):22-27.

[10]邱应强，冯桂，田晖.利用整数变换的高效图像可逆信息隐藏方法[J].华侨大学学报(自然科学版)，2014，35(2):136-141.

[11]BHATTACHARYA D，GHOSH A.Optical transformation based image encryption and data embedding techniques using MATLAB[C]∥Proceedings of SPIE-the International Society for Optical Engineering, International Conference on Potics and Photonics.Kolkata：SPIE Press,2015:96-104.

[12]LOKESHWARI G，SUSARLA S，KUMAR S U.A modified technique for reliable image encryption method using merkle-hellman cryptosystem and Rsa algorithm[J].Journal of Discrete Mathematical Sciences and Cryptography，2015，18(3):293-300.

[13]罗明,陈小玲.基于AES算法的彩色数字图像加密技术研究[J].科技风,2014(20):12.

[14]张琼,方若宇，李斌.基于小波变换和混沌映射的彩色图像加密方法[J].电子技术与软件工程,2014(16):135.

[15]叶瑞松,谭相波.基于连续混沌系统多轨道混合的图像加密算法[J].汕头大学学报(自然科学版),2014,29(4):8-20.

[16]吴丽,余文春.快速置乱耦合3D混沌映射的图像加密算法研究[J].电视技术,2014,38(19):51-56.

[17]燕善俊,程德强.一种基于DCT和混沌序列的图像加密算法[J].徐州工程学院学报(自然科学版),2014,29(4):39-43.

(责任编辑： 黄晓楠英文审校： 吴逢铁)

Image Hiding Algorithm Based on 3D Chaotic Mapping

and Bit Information Processing

LI Bingli

(College of Material Science and Engineering， Hengshui University， Hengshui 053000， China)

Abstract：A method of image hiding based on 3D chaotic map and bit information exchange is constructed. This method exchanges the original image of the high and low Bit and Qi mapping form the three dimensions of the chaotic sequence truncation matrix of XOR processing to complete the image information hiding. Experimental results show that the proposed method has good visual hiding effect, and the correlation between the hidden images is very low, and it is also very sensitive to the minor key changes.

Keywords：Image hiding； bit information； Qi chaotic map； three correlation

基金项目：河北省教育科学研究基金资助项目(13041338)

通信作者：李冰立(1982-)，男，讲师，博士，主要从事图像隐藏技术的研究.E-mail:libingli800688@sina.com.

收稿日期：2015-11-13

中图分类号：TP 301.6； TP 391

文献标志码：A

doi:10.11830/ISSN.1000-5013.2016.01.0058

文章编号：1000-5013(2016)01-0058-04