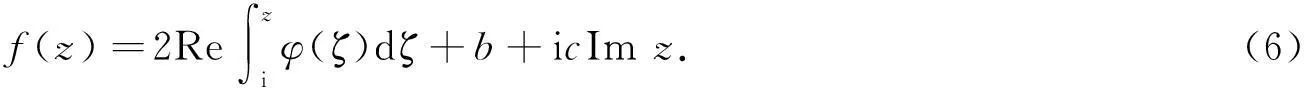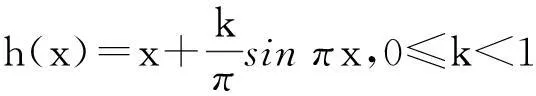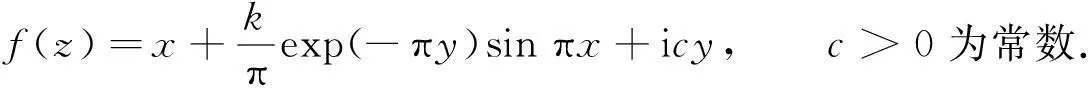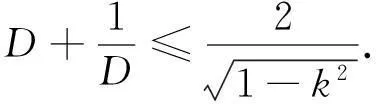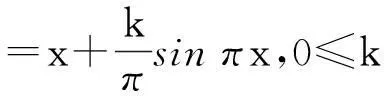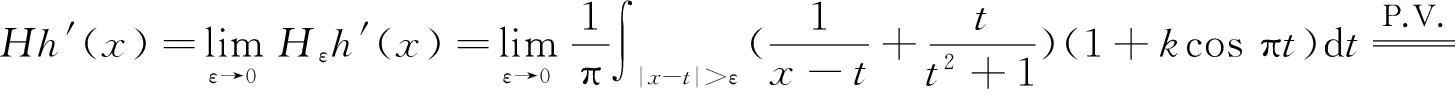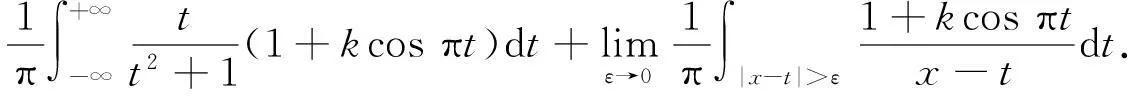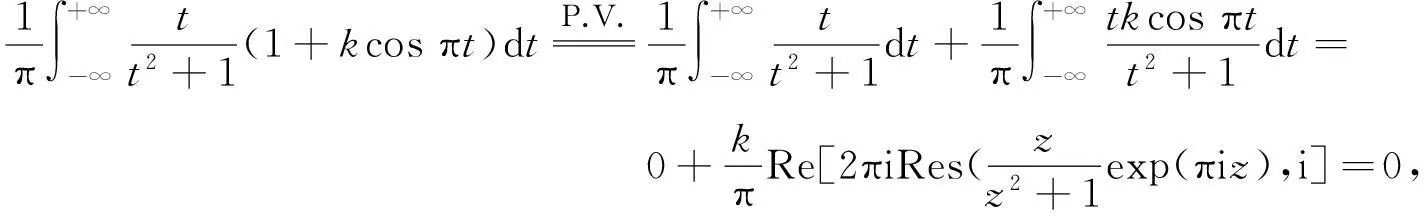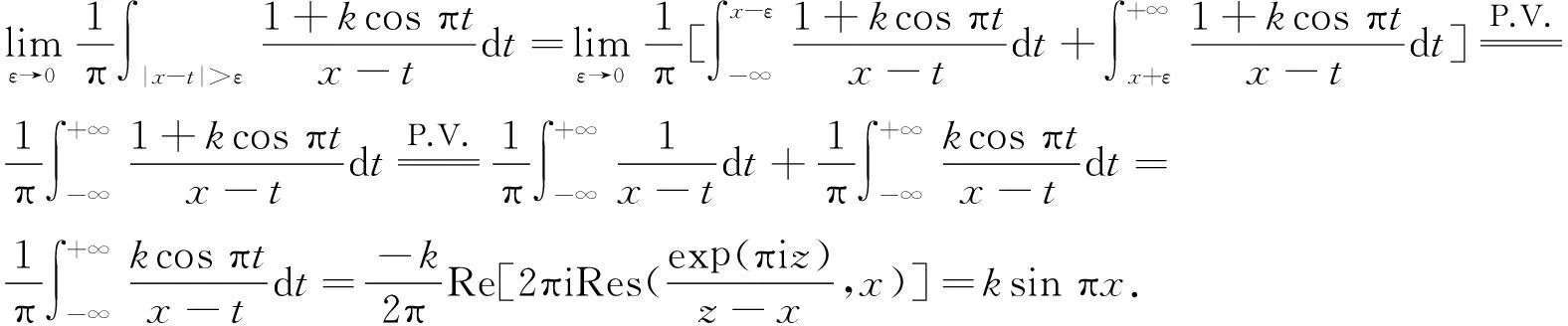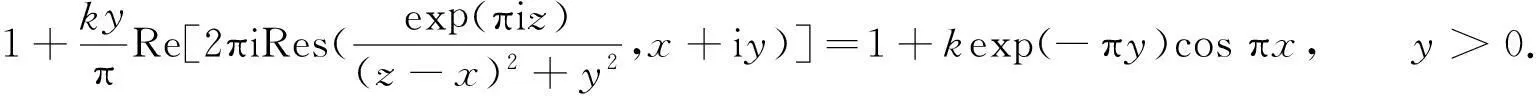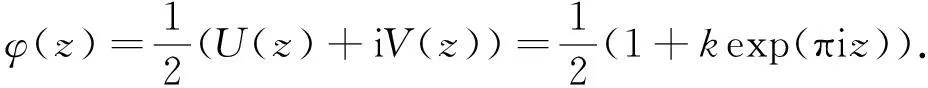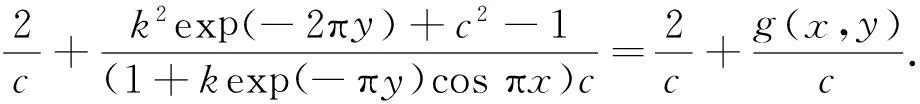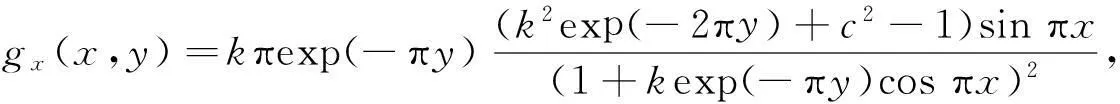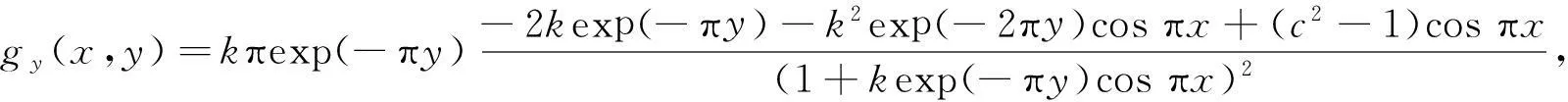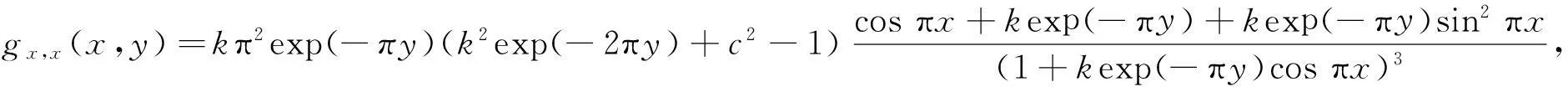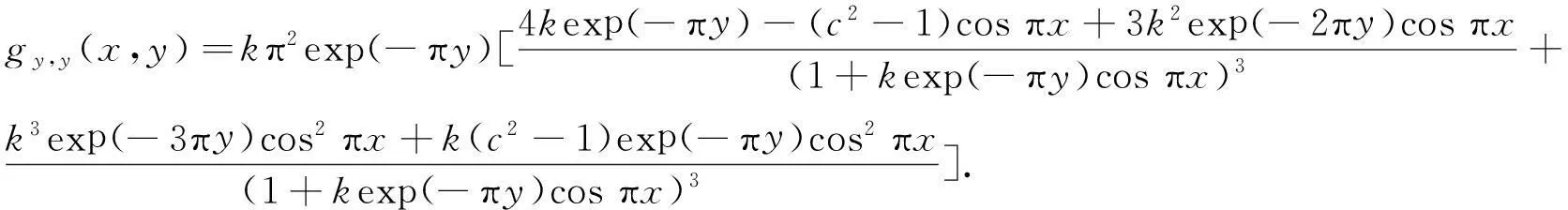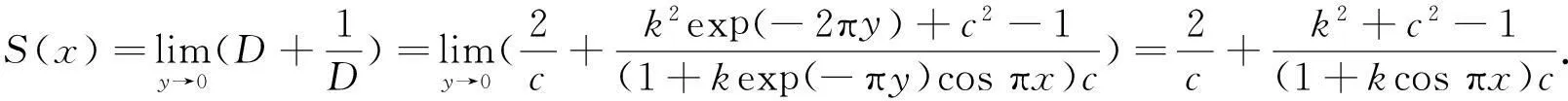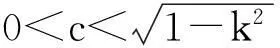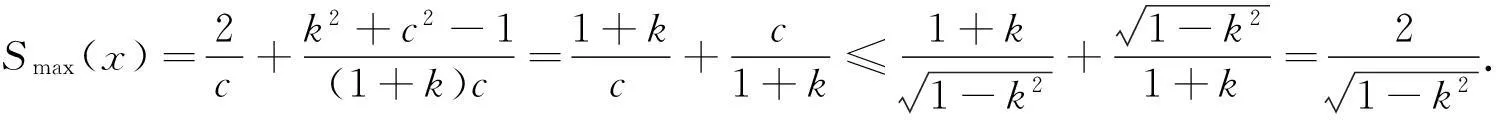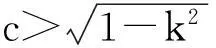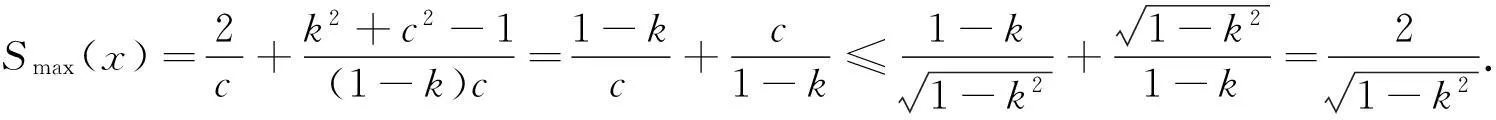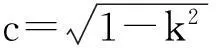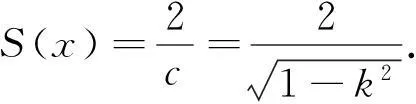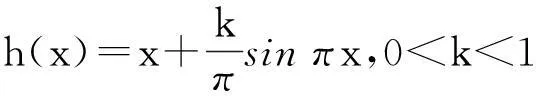上半平面某类调和拟共形映照的特征估计

林珍连

(华侨大学 数学科学学院， 福建 泉州 362021)



上半平面某类调和拟共形映照的特征估计

林珍连

(华侨大学 数学科学学院， 福建 泉州 362021)

摘要：给出以sin πx，0≤k<1为边界值的上半平面到自身的调和拟共形延拓表达式及其特征估计.结果表明:该调和拟共形延拓比Beurling-Ahlfors延拓更优.

关键词：最大特征; 拟共形延拓; 调和拟共形映照; Hilbert变换

1预备知识

拟共形映射的边界对应问题是拟共形映射理论中十分重要的内容，它包括拟共形映照边界函数和给定边界函数的拟共形延拓问题的研究，这些都有利于拟共形映照理论中极值问题的研究.

平面区域Ω到G的可微拓扑映照f:(x,y)→(u,v)，其特征D定义为

若D是有界的,则称f是拟共形的，D的最小上界称为最大特征[1].

实轴R到自身一个连续的严格递增函数h(x),称为ρ-拟对称的,ρ≥1.若对一切x∈R,t>0，有

记H={z|Imz>0}.Beurling等[1]证明了h(x)具有H到H上的拟共形延拓的充分必要条件，是h(x)为ρ-拟对称函数,并建立Beurling-Ahlfors扩张函数为

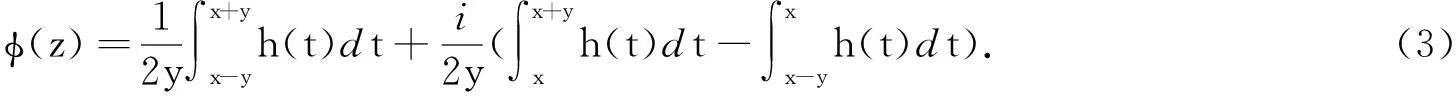
关于Beurling-Ahlfors延拓特征估计问题，一直以来吸引了众多国内外学者的眼球[1-2].迄今为止,最大特征D的最好估计是D≤max{2ρ-1,ρ3/2}[2].

Douady等[3]讨论了单位圆到自身的边界对应问题，利用调和测度给出延拓表达式，并且讨论了它的特征估计尽管十分粗糙.Reich[4]用参数表示法对这一问题进行了探讨，然而，他的特征估计也不是最佳的.文献[5-6]分别讨论了单位圆及上半平面到自身的调和拟共形延拓的边界对应问题,给出可延拓成单位圆或上半平面到自身的调和拟共形的边界对应所满足的充要条件，但没有涉及到特征估计.

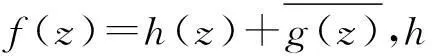
定义h(x)∈L∞(R)的Hilbert变换为

式(4)中：

Hh(x)几乎处处存在，但Hh(x)未必属于L∞(R)[10-11].

称h(x)是双李普希兹的，若h(x)绝对连续且有某个常数c，使得1/c

文献[6]证明了h(x)具有H到H上的调和拟共形延拓的充分必要条件是h(x)是双李普希兹的，且Hh′(x)∈L∞(R).同时，还证明了定理A.

据了解，王宝生1980年就参加了工作，当时才15岁，是个林二代，现在已经在林场工作38年了，2008年王宝生来到了中军帐瞭望台。回忆起刚来的时候，王宝生告诉记者，刚上来觉得一切都还好，可是在这待了一年之后，这里的环境真的有点艰苦。

定理A上半平面到自身的任意调和拟共形延拓具有唯一表示式，即

式(6)中：b+ic∈H；φ是定义在H上的解析函数，满足φ(H)是右半平面的相对紧子集.

由于调和映照的黎曼映照定理不再成立，使式(6)中f(z)的特征估计变得困难.本文就具体给定的边界对应，作出其上半平面到自身的调和拟共形延拓表达式，并对它的特征作出估计.

2主要结论及其证明

其特征D有估计式

分别计算上式两个积分，即

因此，Hh′(x)∈L∞(R).

依据文献[6]的方法，给出h(x)到上半平面的调和拟共形延拓的具体表达式，为此令

设V(z)为U(z)满足V(i)=0的共轭调和函数，则V(z)=kexp(-πy)sinπx,解析函数为

显然,φ(H)是右半平面的相对紧子集，根据定理A，有

证明g(x,y)在上半平面是次调和的.经过计算，有

因此，有

4kexp(-πy)cosπx+2k2exp(-2πy))>0.

也就是说，D+1/D在上半平面H上是次调和的.因而，它的最大值只能在边界上达到.令

求S(x)的最大值.

3结束语

参考文献：

[1]BEURLING A,AHLFORS L.The boundary correspondence under quasiconformal mappings[J].Acta Mathematica,1956,96(1):125-142.

[2]LEHTINEN M.Remarks on the maximal dilation of Beurling-Ahlfors extension[J].Ann Acad Sci Fenn AI Math,1984(9):133-139.

[3]DOUADY A,EARLE C J.Conformally natural extension of homeomorphisms of the circle[J].Acta Mathematica,1986,157(1):23-48.

[4]REICH E.A quasiconformal extension using parametric representation[J].Journal d Analyse Mathématique,1990,54(1):246-258.

[5]PAVLOVIC M.Boundary correspondence under harmonic quasiconformal homeomorphisms of the unit disks[J].Ann Acad Sci Fenn Math,2002,27(2):365-372.

[6]KALAJ D,PAVLOVIC M.Boundary correspondence under quasiconformal harmonic diffeomorphisms of a half-plane[J].Ann Acad Sci Fenn Math,2005,30(1):159-165.

[7]LEWY H.On the non-vanishing of the Jacobian in certain one-to-one mappings[J].Bulletin of the American Mathematical Society,1936,42(10):689-692.

[8]DUREN P.Harmonic mappingd in the plane[M].Cambridge:Cambridge University Press,2004:479,481-506.

[9]CLUNIE J,SHELL-SMALL T，CLUNIE J.Harmonic univalent functions[J].Ann Acad Sci Fenn Ser A I Math,1984(9):3-25.

[10]GARNETT J B.Bounded analytic function[M].New York:Academic Press,1981:1-406.

[11]林珍连.某些调和单叶函数的稳定性及系数估计[J].华侨大学学报(自然科学版)，2009，30(6)：718-719.

(责任编辑： 黄晓楠英文审校： 黄心中)

Dilatation Estimate for Some Kinds of Harmonic

Quasiconformal Mappings of the Half Plane Onto Itself

LIN Zhenlian

(School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China)

Keywords：maximal dilatation; quasiconformal extension; harmonic quasiconformal mapping; Hilbert transformation

基金项目：国家自然科学基金资助项目(11471128); 国家青年科学基金资助项目(11501220); 福建省自然科学基金计划资助项目(2014J01013)； 华侨大学中青年教师科研提升资助计划(ZQN-YX110)

通信作者：林珍连(1970-)，女，副教授，主要从事函数论的研究.E-mail:zhenlian@hqu.edu.cn.

收稿日期：2015-08-25

中图分类号：O 174.55

文献标志码：A

doi:10.11830/ISSN.1000-5013.2016.01.0125

文章编号：1000-5013(2016)01-0125-04