基于自适应反演滑模的四旋翼飞行器姿态控制研究

曹开发，谢慕君，李元春

（长春工业大学 电气与电子工程学院，长春 130012）

近年来，随着地震、洪水、火灾、核污染等大型自然灾害及事故的贫发，四旋翼无人机的研究越来越受到研究机构、高校、企业的重视。它的体积小，操作简单，结构灵活能够在狭小的空间里进行垂直起飞、翻转、前进、后退、悬停等特点。因此在军用和民用领域具有广泛的应用前景，如低空侦察、灾害现场监视与救援、航拍测绘、管线巡检等。

由于飞行器姿态的控制直接决定飞行器控制效果，所以姿态控制显得尤为重要。目前姿态控制算法有模糊自整定PID控制[1]、滑模控制[2-4]、动态逆控制[5]、线性二次高斯控制[6]。然而飞行器在实际的飞行过程中会受到外界的不确定干扰，为了提高系统的鲁棒性和响应速度，本文假设四旋翼飞行器实现定高悬停的条件下建立动力学模型，采用自适应的反演滑模控制，并在Matlab/Simulink平台上进行仿真，验证算法。

1 四旋翼飞行器的模型

1.1 四旋翼飞行器的介绍

本文采用的四旋翼飞行器是一个四输入三输出的对象，系统具有3个自由度，其输出飞行是俯仰角、翻转角、巡航角。系统输入是4个电机的输入电压。4个电机中前、左、右3个电机的浆是上下朝向，后面的一个电机的浆是左右朝向。支架的中心处安装了集电环，这样整个支架就能在水平方向任意角度旋转，系统的姿态角度由平台上的角度编码器检测获得[7]。

1.2 四旋翼模型的方程

1.2.1 参考坐标

四旋翼飞行器建立坐标如图1所示。

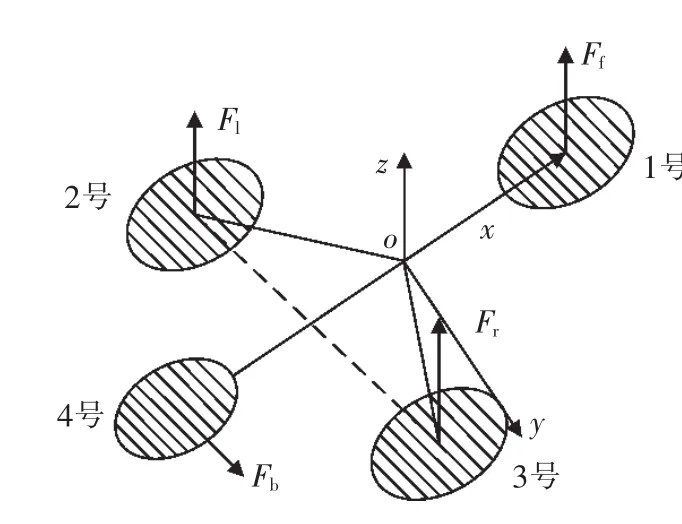
图1 四旋翼飞行器力学坐标Fig.1 Four-rotor aircraft mechanics plot

其中，坐标原点位于支撑点，指向正前方电机为x轴，指向右侧电机为y轴，从而确定坐标系z轴正方向，定义正前方、左、右电机转动，带动螺旋桨运动产生的力，与z轴同向为正向。尾部电机转动带动螺旋桨运动产生力，与y轴同向为正向。其中：Ff为前向电机的升力；Fl为左侧电机的升力；Fr为右侧电机的升力；Fb为尾部电机的力[7-8]。

1.2.2 平衡方程

建立平衡方程，并做以下假设：

1）假设系统处于静平衡状态，3个姿态角均为0，并忽略摩擦力、电机阻尼力矩；

2）忽略电机达到给定转速的时间；

3）假设螺旋桨正反转时产生的力一样。

A.俯仰角力矩平衡方程

俯仰角静平衡受力分析如图2所示，定义俯仰角为前电机向下运动夹角为正。

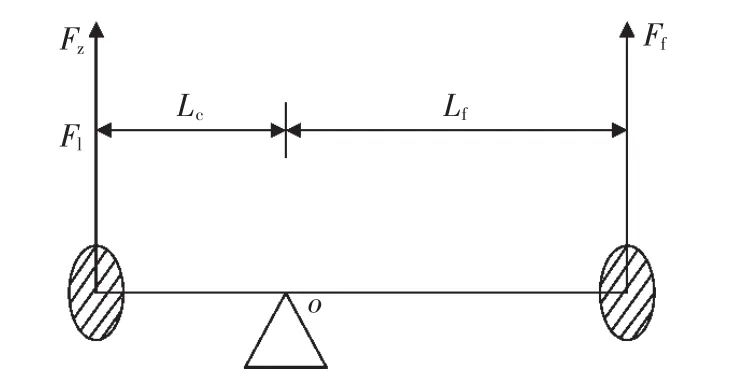
图2 俯仰角力学分析图Fig.2 Pitch angle mechanics analysis diagram

其力矩平衡方程为

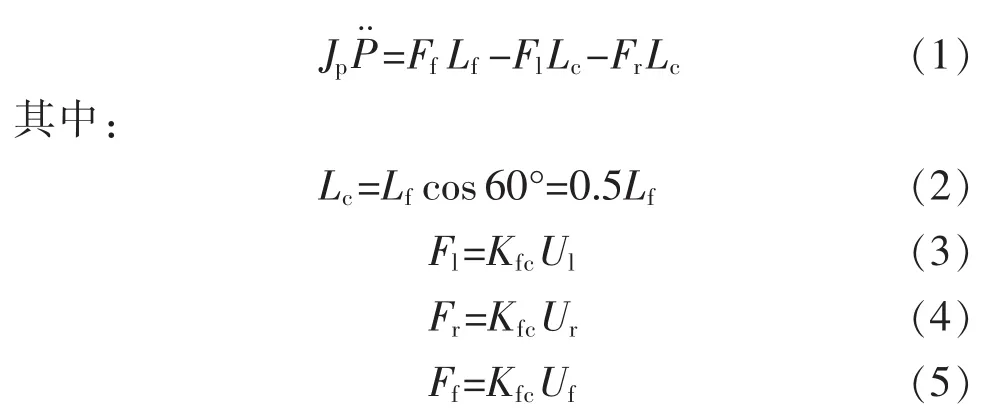
将式（2）、（3）、（4）、（5）代人式（1）简化从而得到：

B.翻转角力矩平衡方程

滚转角静平衡受力分析如图3所示，定义滚转角为右侧电机向下运动夹角为正。

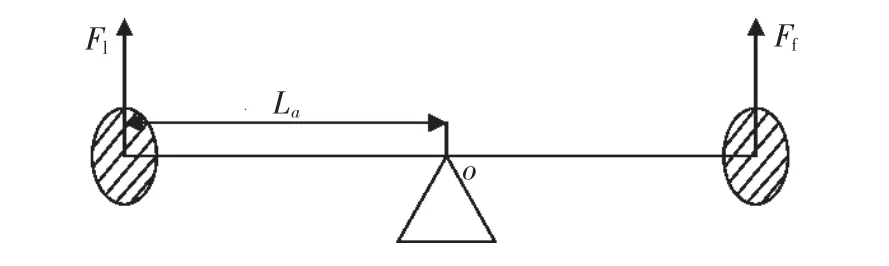
图3 翻转角力学分析图Fig.3 Roll angle mechanics analysis diagram

其力矩平衡方程为

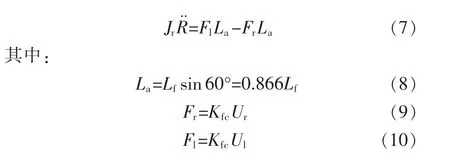
将式（8）、（9）、（10）代入式（7）并简化可得：

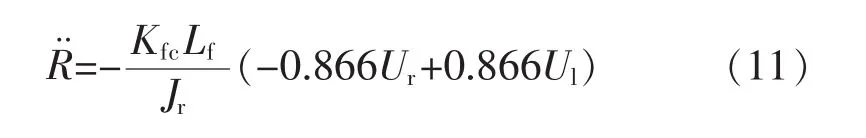
C.偏航角力矩平衡方程

定义偏航角为绕z轴顺时针运动角度为正，则建立如下方程：

式中：Jy为四旋翼飞行器绕z轴转动惯量；为巡航角的角加速度。

D.高度平衡方程

当四旋翼为初始状态时：

当四旋翼飞行时：

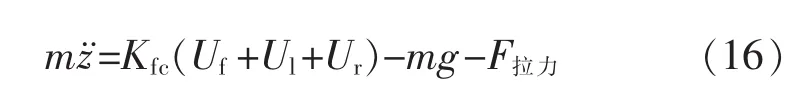
然而当四旋翼处于定高悬停时，F拉力＝0，式（16）可简化为

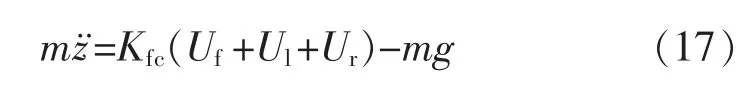
四旋翼飞行器的物理参数如表1所示。

表1 四旋翼飞行器的物理参数表Tab.1 Physical parameter values of quad-rotor

将表中的参数代人式 （6）、（11）、（14）、（17）可得到：

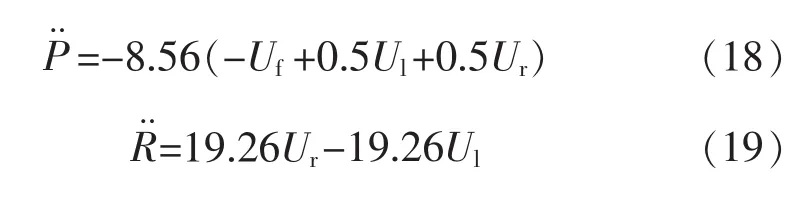
这样就将数学模型变为偏航、俯仰、翻转、高度4个通道，下面就可以考虑各个通道中存在未知干扰的情况，于是可变为

式中：Δ1，Δ2，Δ3，Δ4为各个通道的未知干扰。

2 四旋翼控制器设计

2.1 反演滑模控制器

设系统模型状态变量为

以俯仰角控制律设计为例，假设位置为Yd，跟踪误差为z1，控制器设计步骤如下[9-10]：

步骤1：

对于位置跟踪，跟踪误差为

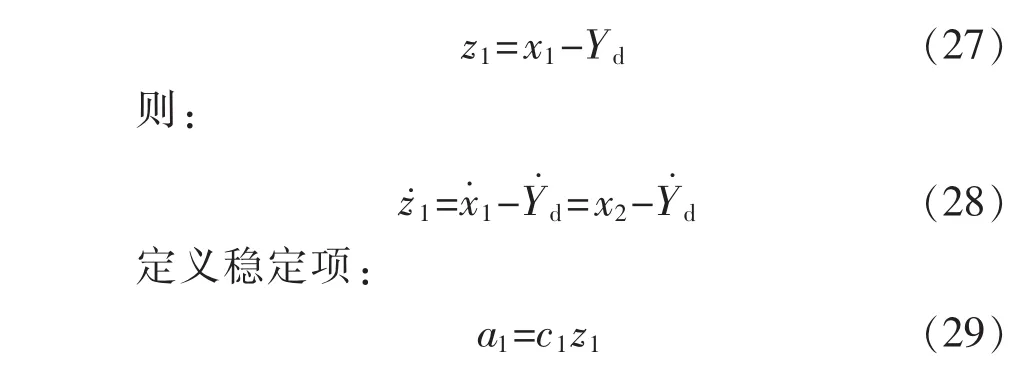
其中，c1为正的常数。

定义Lyapunov函数：

其中，k1＞0，则：

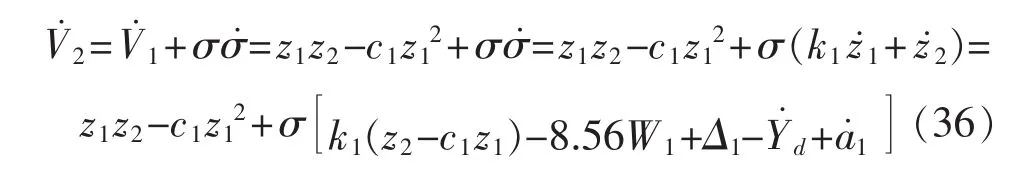
2.2 不确定上界的估计

一般控制对象的不确定因素的上界值很难预知，为了避免采用Δ1的上界问题，采用自适应算法预估Δ1的值。

定义Lyapunov函数：

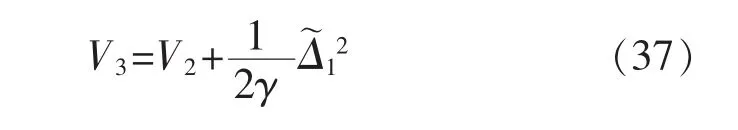
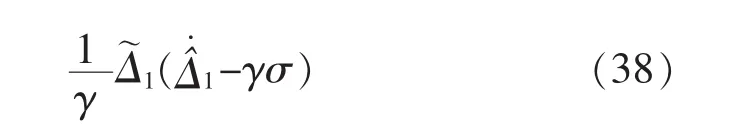
设计自适应控制器为

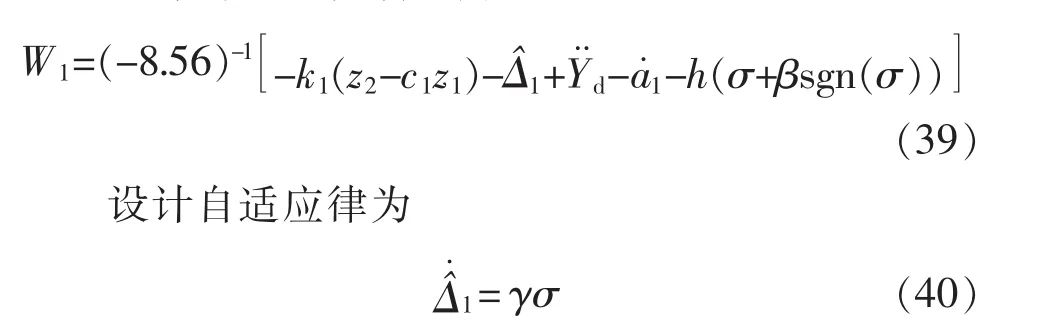
2.3 稳定性分析

把式（39）、（40）代人式（38）得到：

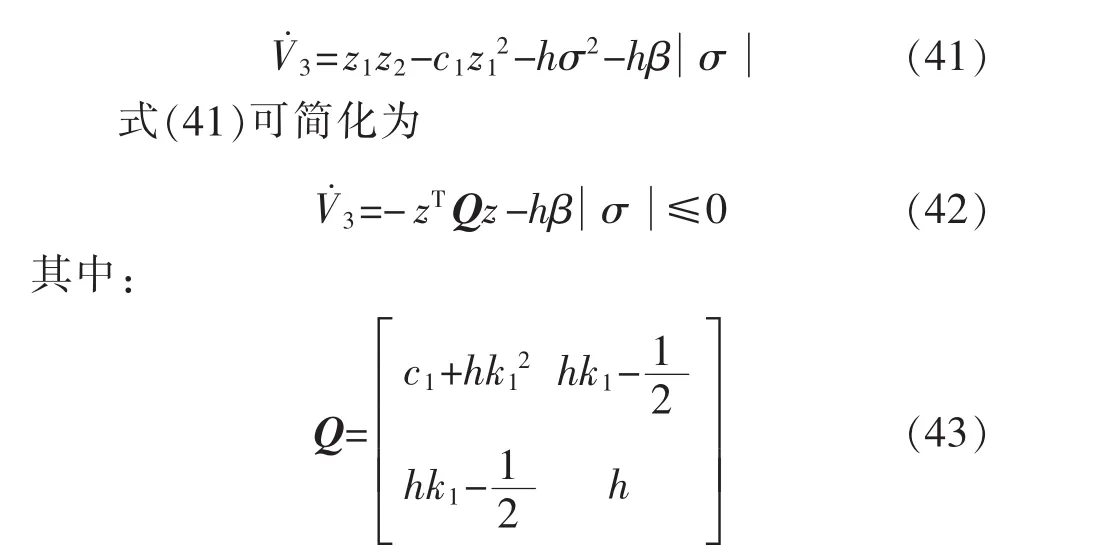
通过取 h，c1，k1的值，可使|Q|＞0，从而保证Q为正定矩阵。

3 仿真与分析

为了对设计的算法进行验证，以四旋翼飞行器为例，仿真结果如下：

1）当采用常规反演滑模控制

当外部扰动为 Δ（1，2，3，4）=2sin（t），取β=1，h=4，c1=18，k1=10，当输入幅值为 1，频率为 2π的正弦时，3个角度仿真结果如图4所示。

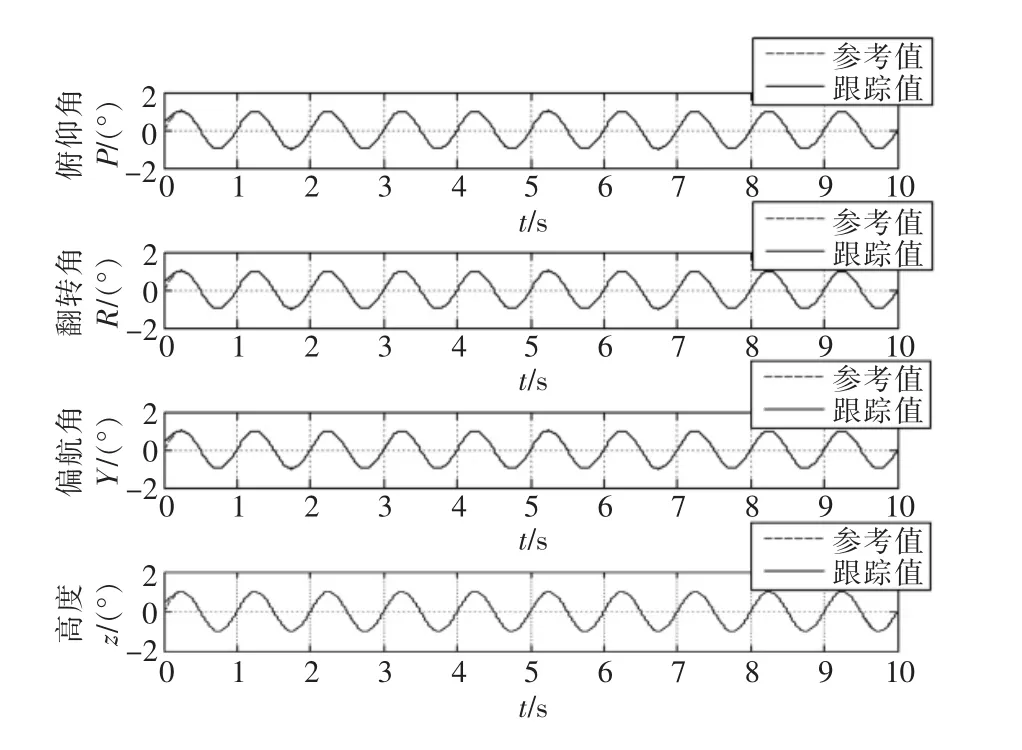
图4 姿态角与高度的跟踪信号Fig.4 Attitude angle and height of the tracking signal

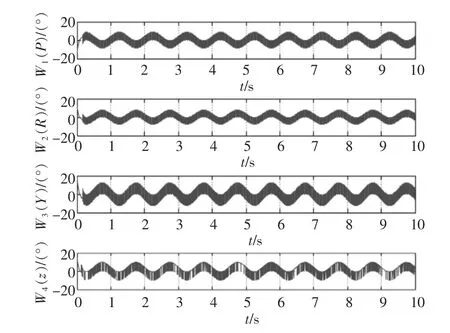
图5 姿态角与高度的控制律Fig.5 Attitude angle and height of control law

图6 姿态角与高度的跟踪误差Fig.6 Attitude angle and height of the tracking error

2）当采用自适应反演滑模控制

当不确定 Δ（1，2，3，4）=2sint，γ=800，h=4，c1=18，k1=10，β=1，当输入为幅值为 1，频率为 2π 的正弦时，3个角度仿真结果如图7所示。

图7 姿态角与高度的跟踪信号Fig.7 Attitude angle and height of the tracking signal

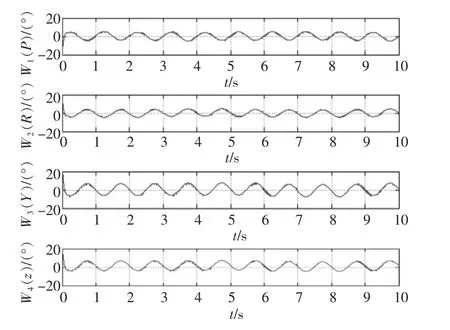
图8 姿态角与高度的控制律Fig.8 Attitude angle and height of control law

图9 姿态角与高度的跟踪误差Fig.9 Attitude angle and height of the tracking error

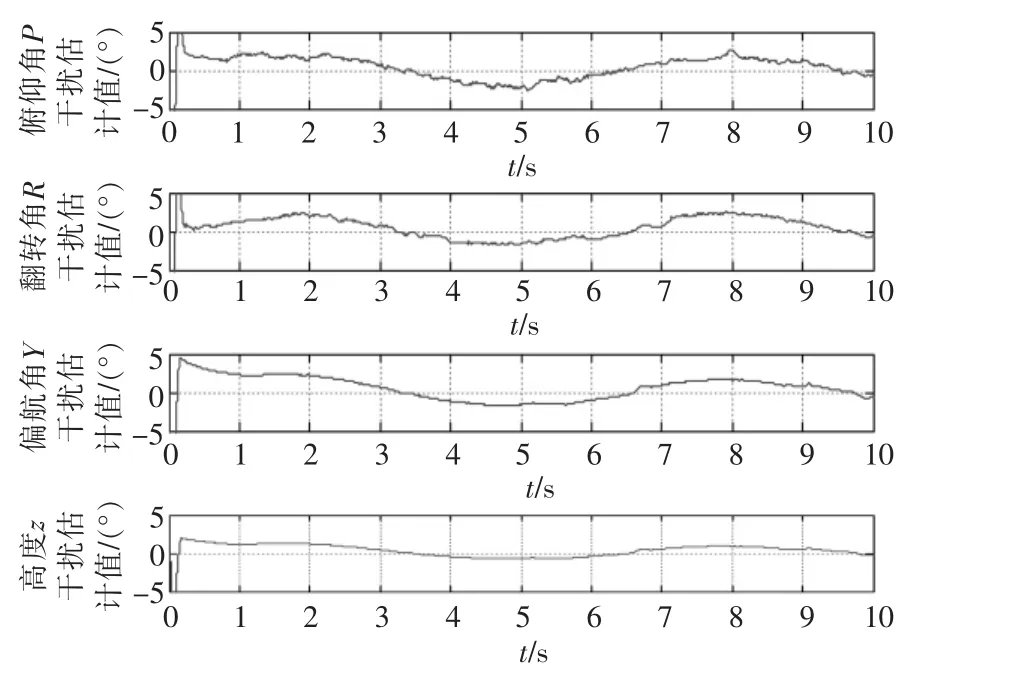
图10 姿态角与高度的估计值Fig.10 Attitude angle and height of the estimated value

通过图4、图7可以看出姿态角和高度的实际输出值与期望输出值，可以得出系统的俯仰角、滚转角、偏航角和高度都能够有效地跟踪期望的值，通过图6、图9可以得出2种方法下的误差都能够在较短时间里收敛，然而在常规反演控制中的姿态角收敛时间大约在0.3 s，自适应反演滑模控制的收敛时间小于0.3 s。

图5与图8可以看出常规控制下俯仰角、翻转角、偏航角和高度的控制律都发生剧烈抖振，俯仰角的抖振幅值为8.5，翻转角的抖振幅值为4.2，偏航角的抖振幅值为12，高度的抖振幅值为25，而自适应反演控制下的抖振幅值分别为4.8、2.4、6、18。所以自适应反演控制下的姿态角的抖振大大降低。

4 结语

以四旋翼无人机作为研究对象，建立四旋翼飞行器姿态的动力学模型，对模型进行简化，通过设计自适应反演滑模控制，解决了在未知干扰情况下的四旋翼无人机的姿态跟踪控制和抖动问题。通过仿真结果可以看出，达到了预期的控制效果。

[1]李一波，宋述锡.基于模糊自整定PID四旋翼无人机悬停控制[J].控制工程，2013，20（5）：910-914．

[2]李波波，贾秋玲.基于滑模控制器的四旋翼飞行器控制器设计[J].电子设计工程，2013，21（6）：76-78．

[3]Daewon Lee，H Jin Kim，Shankar Sastry.Feedback linearization vs adaptive sliding mode control for a quadrotor helicopter[J].International Journal of Control，Automation，and Systerms，2009，7（3）：419-428．

[4]丛炳龙，刘向东，陈振.一种改进的自适应滑模控制及其在航天器姿态控制中的应用[J].控制与决策，2012，27（10）：1-6．

[5]章志祥，王立峰，赫丛奎.基于自适应动态逆的四旋翼机器人控制设计[J].动力系统与控制，2014（3）：1-7．

[6]陈炜峰，朱海飞，王伟，等.基于线性二次高斯的四旋翼飞行器姿态控制[J].控制工程，2014，21（1）：120-124．

[7]魏吉敏.四旋翼飞行器的建模及预测控制研究[D].长沙：中南大学，2013．

[8]固高公司.四旋翼仿真实验指导[M]，2012．

[9]刘金坤.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社，2005．

[10]魏丽文.四旋翼飞行器控制系统设计[D].哈尔滨：哈尔滨工业大学，2010．