高维蛋白质波谱癌症数据特征提取

高维蛋白质波谱癌症数据特征提取

吴文峰，刘毅慧*

(齐鲁工业大学信息学院，济南 250353)

摘要：高维蛋白质波谱癌症数据分析，一直面临着高维数据的困扰。针对高维蛋白质波谱癌症数据在降维过程中的问题，提出基于小波分析技术和主成分分析技术的高维蛋白质波谱癌症数据特征提取的方法，并在特征提取之后，使用支持向量机进行分类。对8-7-02数据集进行2层小波分解时，分别使用db1、db3、db4、db6、db8、db10、haar小波基，并使用支持向量机进行分类，正确率分别达到98.18%、98.35%、98.04%、98.36%、97.89%、97.96%、98.20%。在进一步提高分类识别正确率的同时，提高了时间率。

关键词：小波分析；主成分分析；蛋白质波谱；降维；分类

中图分类号：Q629.73文献标志码：A

Feature selection for high-dimensional cancer protein mass spectrometry data

WU Wenfeng,LIU Yihui*

(SchoolofInformation,QiluUniversityofTechnology,Jinan250353,China)

Abstract：The analysis of high-dimensional cancer protein mass spectrometry data is full of trouble from high-dimensional data.We propose method for selecting the feature of high-dimensional cancer protein mass spectrometry data based on the wavelet analysis and principal component analysis,and solving the faled problems when we reduce the dimensionality of high-dimensional cancer protein mass spectrometry data.After feature selection,we use the support Vector Machine(SVM) for classification.We use wavelet decomposition on 8-7-02 data set at second level,use different wavelet basis(db1,db3,db4,db6,db8,db10,haar) and classify them with the SVM, then we get different recognition rates:98.18%,98.35%,98.04%,98.36%,97.89%,97.96%,98.20%.Improve the classification accuracy and the efficiency of time simultaneously.

Keywords：Wavelet analysis;Principal component analysis;Protein mass spectrometry;Dimensionality reduction;Classify

近年来，蛋白质组学迅速发展。蛋白质波谱数据分析在癌症检测中得到了越来越广泛的应用。目前，在蛋白质波谱分析过程中，波谱信息主要通过基质辅助激光解析电离技术(Matrix-Assisted Laser Desorption/Ionization:MALDI)和表面增强激光解吸离子化飞行时间质谱技术(Surface-Enhanced Laser Desorption/Ionization Time-of-Flight Mass Spectrometry:SELDI-TOF-MS)来获得[1]。本文中的蛋白质波谱数据，主要是通过SELDI-TOF-MS技术得到。SELDI-TOF-MS技术主要由蛋白质芯片、飞行时间质谱仪和相关软件组成，其中蛋白质芯片是该技术的核心。

严勇等通过采用模式识别领域常用的决策树与AdaBoost技术来处理医学领域常用的质谱分析数据[2]，研究了弱分类器个数对分类性能的影响，将AdaBoost与支持向量机进行类比。根据实验，从大间隔学习的角度，阐述了AdaBoost的优势。AdaBoost是二元分类方法中经常用到的一个提升方法[3]。AdaBoost对不同训练集训练时，采用同一个弱分类器，之后把在不同训练集上得到的分类器集合起来，组成一个更优的强分类器。邹修明等在基于蛋白质的癌症诊断实验中[4]，通过基线校正和标准化，并使用分箱法对原始数据进行降维预处理，之后使用T检验方法来选取特征，对经过了一系列处理后的蛋白质质谱数据进行分析研究。论文中实验采用10-fold交叉验证和支持向量机对卵巢质谱数据集进行分类。杨合龙等针对如何有效分析高通量SELDI-TOF质谱数据以及筛选与肿瘤相关的蛋白质位点，提出一种基于近邻传播聚类分析 的特征选选择方法[5]。Kuehl B 等将蛋白质波谱分析应用于细菌生理研究，并结合主成分分析方法，区分细菌的不同生理状态[6]。EBERLIN L等利用蛋白质波谱数据研究人类脑瘤，对正常和患病数据进行分类[7]。王昭鑫等针对癌症蛋白质谱数据中包含大量未知的内部结构和变量这一特点，在总结主元余像集主成分分析(二次主成分分析)应用的基础上，提出了应用t-验证方法进行特征子集选取，之后用主元余像集主成分分析来提取特征，最后以线性判别分析进行分类的新方法[8]。

模式识别和分类的过程中，数据特征的质量对于识别和分类的速率和正确率至为重要。需要预先对数据进行降噪、降维、归一化等预处理，之后再提取特征，最后基于降维后的特征来进行模式的识别和分类。目前常用的数据降维降噪处理的方法有主成分分析法、T-test法、Boosting、遗传算法、模拟退火算法、小波分析法等[9-14]。小波分析技术可以用于蛋白质质谱数据的分析，用它做降维去噪处理后的低频系数，可以有效的表征蛋白质质谱数据的特征信息。

高维数据的降维和特征提取方法研究依然很重要。本文将离散小波分析和主成分分析方法相结合，对几组癌症数据进行多维降噪处理，提取低频系数作为其特征数据。在小波分析过程中，对高维蛋白质波谱数据进行不同层的小波分解和基于不同小波基的分解，并做了详细的比较，选择出具有最佳识别率的分解层数和小波基。在之后的主成分分析过程中，通过实验比较，选择出最佳主成分。本文中将使用支持向量机对提取的特征数据进行分类。

1相关理论

1.1小波分析技术

时频分析，是时频联合域分析的简称。它提供了信号的时间域和频率域的联合信息，描述信号频率随着时间变化的关系。

小波分析是时频分析的一种，它在时域和频域里都能很好的表征局部信号特征，是一种多尺度信号分析方法。小波作为一重要的线性时频展开方法，不同于短时傅里叶(Fourier)变换，它是将信号展开为持续时间很短的高频基函数和持续时间较长的低频基函数，而这些不同的基函数是从单个原象小波通过平移和伸缩得到。小波又分两大类：连续小波和离散小波。

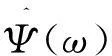
(1)

称Ψ是一个基小波或者称作母小波，其中，R为实数，t为时间。把基小波伸缩和平移，可以得到一个小波序列

(2)

其中，a,b∈R,并且a≠0。a称为伸缩因子，b称为平移因子。式子

(3)

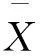
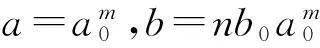
(4)

本文中，采用了离散小波变换，其中，Z为整数。

小波分析中，选择一个小波基并确定一个小波分解的层次N，然后对已知信号进行N层小波分解，如图1所示为小波分解示意图以及部分小波基，图2、图3分别为小波分解前后数据信号波形。

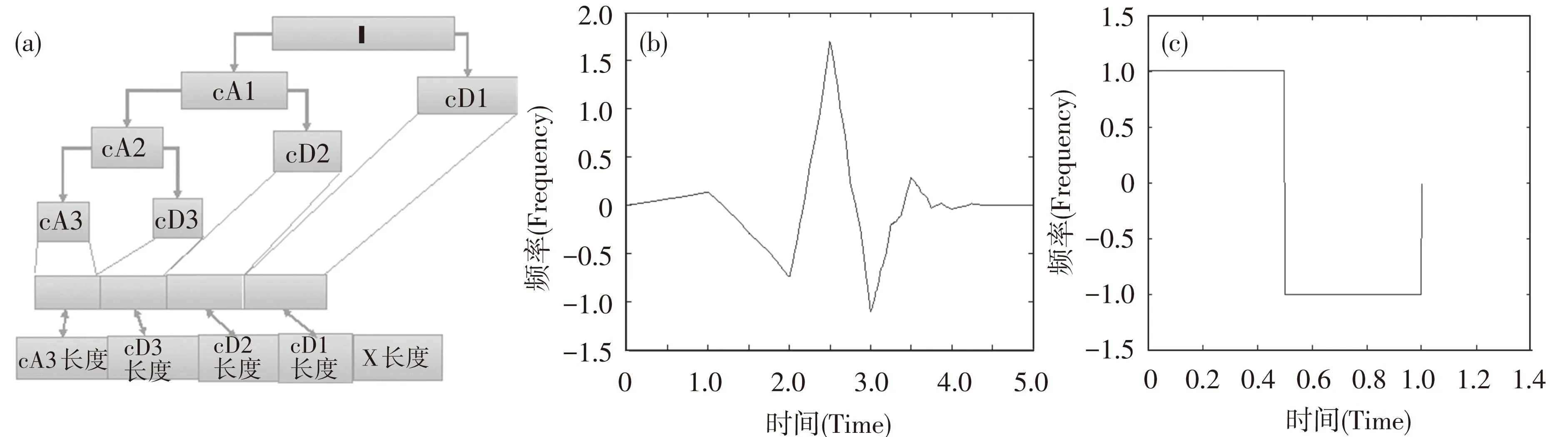
图1　小波分解及小波基

注：图(a)为小波分解：原始信号X经过一次分解后，得到高频系数cD1和低频系数cA1。之后再次对低频系数进行分解，每次分解都会得到高、低频系数。图(b)为db3小波。图(c)为haar小波。

Notes:(a) is wavelet decomposition:fter first level wavelet decomposition on x,we get high frequency coefficient cD1 and low frequency coefficient cA1.Then decompose high frequency coefficient again,we will get high frequency coefficient and low frequency coefficient every decomposition. (b) is db3 wavelet basis. (c) is haar wavelet basis.

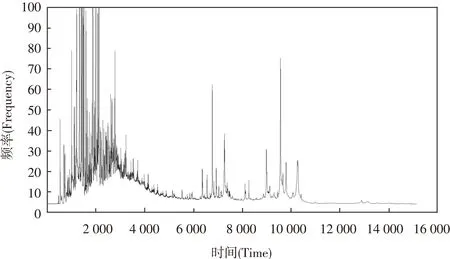
图2　8-7-02数据集第一组数据原始信号波形

注：数据有15 154个属性，作为Time轴，属性值作为Frequency轴。

Notes:The original waveform of the first series data of 8-7-02 data set:the data set has 15 154 properties,set the properties as Time axis, property values as Frequency axis.

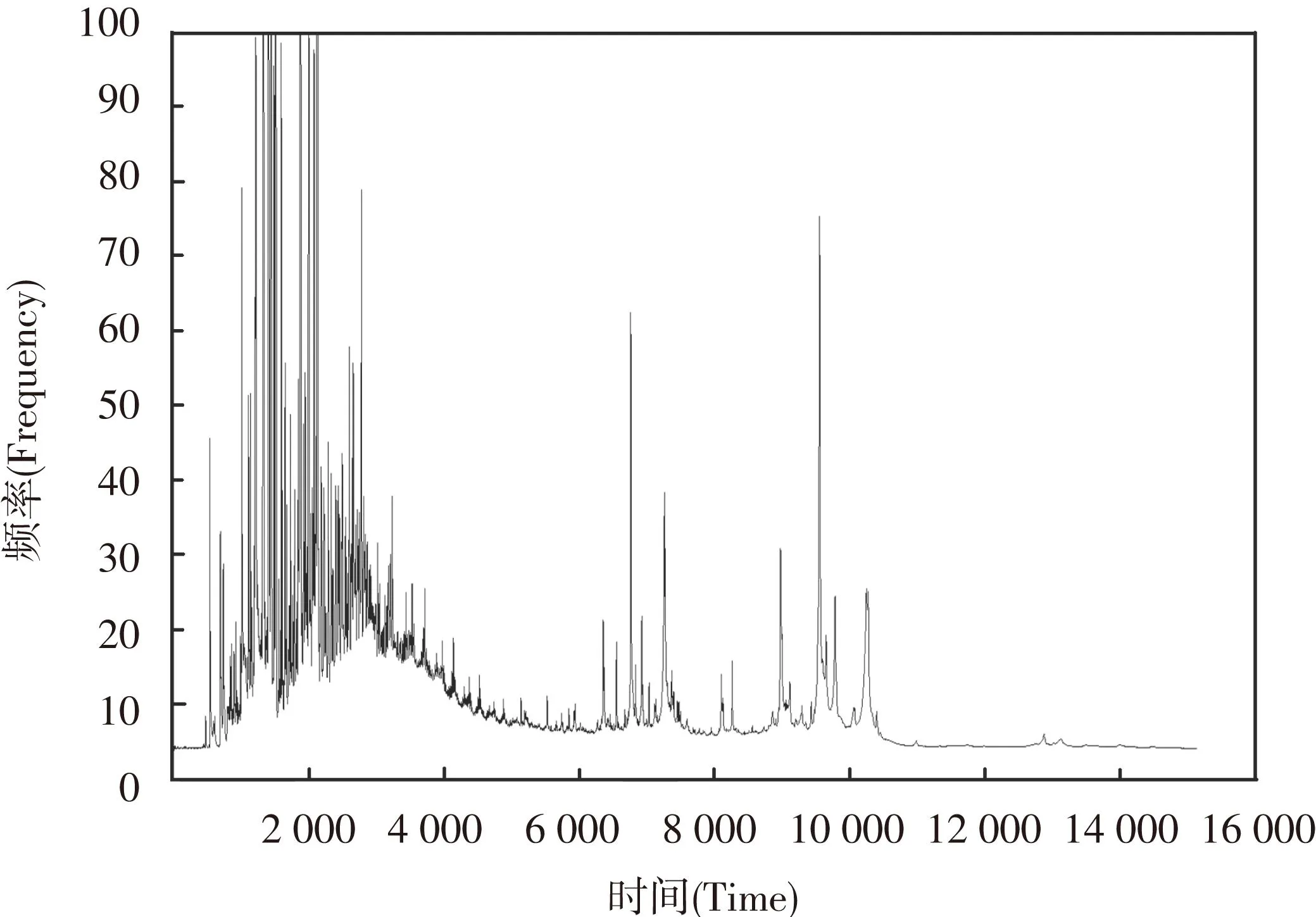
图3　8-7-02数据集第一组数据处理后波形

注：采用db3小波基、4层作为参数进行小波分解后波形，此时数据剩余951个属性。

Notes:After fourth level wavelet decomposition on the first series data of 8-7-02 data set,use db3 wavelet basis:the data has 951 properties now.

1.2主成分分析

主成分分析(Principal component analysis,PCA)最早由皮尔逊(Pearson,1901)引入，后来由霍特林(Hotelling,1933)进一步发展。它是将多个线性相关变量压缩为少数几个不相关的变量的一种多元统计方法，最早由Pearson在研究对空间中的数据进行最佳直线和平面拟合时提出[16]。它通过提出严格线性相关或相关性较强的自变量的信息，选择其中某些维度来表征原有数据，以此达到降维的目的。通常，它对数据各维度进行信息贡献率的计算，并对数据维度按照贡献率排序。之后，可以根据需要自行选取特定的维度来表征原始数据。

假设问题中有p个指标，把这些指标看成p个随机变量X1，X2，…,Xp,主成分分析是要把这p个指标问题转化为p个指标的线性组合问题。这些新指标F1，F2，…,Fk(k≤p),遵循保留主要信息量原则来反映原来指标信息，并且它们相互之间独立。

满足如下条件：

(1)每个主成分系数平方和是1，即

(2)主成分之间相互独立，即

(3)主成分的方差递减，重要性递减，即

F1、F2…Fp分别称为原始变量的第一、第二、第p个主成分。如图4所示为主成份分类散点图：

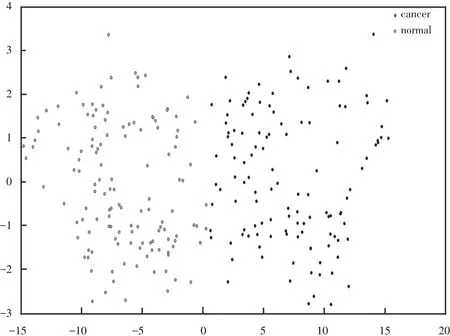
图4　8-7-02 数据集分类结果散点图

注：黑色点为癌症数据，灰色点为正常数据。

Notes:Black dots are cancer datas,grey dots are normal datas.

1.3支持向量机

支持向量机(Support Vector Machine，SVM)从线性可分情况下的最优分类面发展而来。最优分类面就是要求分类线不但能将两类正确分开(训练错误率为0),且使分类间隔最大。支持向量机考虑寻找一个满足分类要求的超平面,并且使训练集中的点距离分类面尽可能的远,也就是寻找一个分类面使它两侧的空白区域(Margin)最大[17]。

1.4K折交叉验证

交叉验证(K-fold cross-validation)是机器学习数据重抽样常用的方法，并且被广泛使用。交叉验证主要有三种，Handout验证、k折交叉验证(K-fold cross-validation)、留一验证(Leave-m-out)。本文主要使用k折交叉验证(K-fold cross-validation)。其基本过程为：将样本集随机分为K个集合，通常分为K等份，对其中的K-1个集合进行训练，剩下的一个集合用来在分类器中进行样本测试。该过程重复K次，取K次过程中的测试错误的平均值作为推广误差。

2实验

2.1实验数据

本实验中，总共使用了三组SELDI-TOF蛋白质质谱数据集来测试分类器的性能。三组数据集中有一组高分辨率卵巢癌数据集、两组低分辨率卵巢癌数据集。三组数据集来源于文献[18]。这些数据在文献[18]中分别给予了命名，本论文沿用文献[18]中的命名。下面简单介绍这三组数据。

2.1.18-7-02数据集

这组低分辨率卵巢癌数据集在采集数据过程中使用了WCX2蛋白质芯片，然后使用升级的PBSII 型SELDI-TOF质谱仪来生成质谱数据。这组数据集包含 162个卵巢癌样本和91个正常样本。每个样本有15 154个特征。

2.1.2这组数据也是低分辨率卵巢癌数据，亦是采用WCX2蛋白质芯片制备样本的。这组数据集由100个卵巢癌样本和100个正常样本组成。每个样本有15 154 个特征。

2.1.3OvarianCD_PostQAQC数据集

此组为高分辨率卵巢癌质谱数据集。它由ABI Qstar型SELDI-TOF质谱仪生成的非随机卵巢癌样本和正常样本组成。卵巢癌样本121个，正常样本95个。每个样本由15 154个特征组成。

2.2基本思路方法

将数据预处理后，通过小波分析技术进行降维处理，之后使用PCA技术，继续降维，取出主成分属性。然后用支持向量机(SVM)作为分类器，通过k-fold交叉验证，分类数据，并评估其性能。主要过程如图5所示：

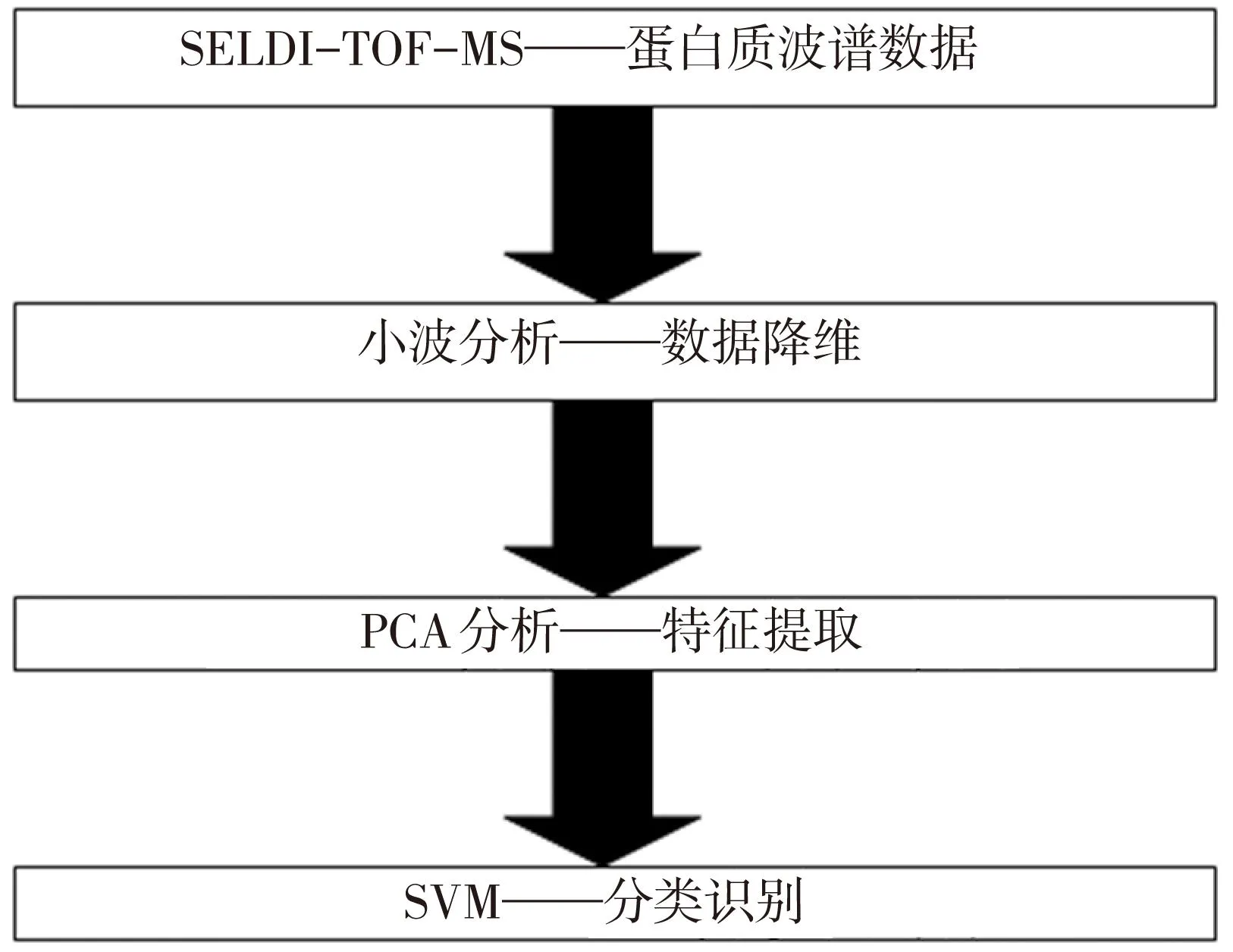
图5　实验流程图

2.3实验

对8-7-02数据集实验结果进行分析。实验过程中，首先，确定PCA分析所取最佳属性，实验中，取能表征数据集90%以上主成分分量的最佳属性。经测试，8-7-02数据集经过小波分析和主成分分析后，前12维属性贡献率之和达到90.61%，故取其前12维属性，如图6所示：

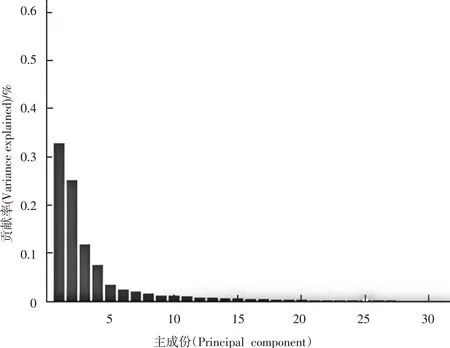
图6　8-7-02数据集部分主要维度属性贡献率

注：前十二维属性贡献率之和为90.61%。

Notes:Sum of the contribution rates of the first twelve properties is 90.61%.

通过图3的思路，对8-7-02数据集进行分类，其中k-fold验证中参数取5，小波变换过程中，分解层数分别取1到5层，小波基分别取haar和dbN小波系。最终得到在不同小波分解层数和不同小波基条件下的分类情况。结果如表1所示：

实验一：取前十二维属性，对比分析不同小波基、分解层数实验效果。

由实验结果数据可以看到，随着小波分解层数增加，分类正确率、灵敏性、特异性都略有下降，每增加一层分解，数据属性维度就会减少一半，数据维度太多或太少，都不能很好的实现分类效果。另外，小波分解之后，对得到数据进行主成分分析，数据的前少数属性维即可很好的表征数据特征，不需要太多冗余属性维，这大大降低了数据维度，为之后的分类减轻了很大的负担，极大的提高了效率。最终经实验分析得出，8-7-02数据集在使用db3小波基，小波分解层数为1，取前12维属性时，其分类效果最佳：正确率98.38%，灵敏性98.79%，特异性98.15%。见表1、表2、表3。

实验二：固定小波基和分解层数，对比选取不同主成分属性实验效果。

当分别取前6、9、12维属性，使用db4小波基、3层分解时，实验结果对比如表4所示：

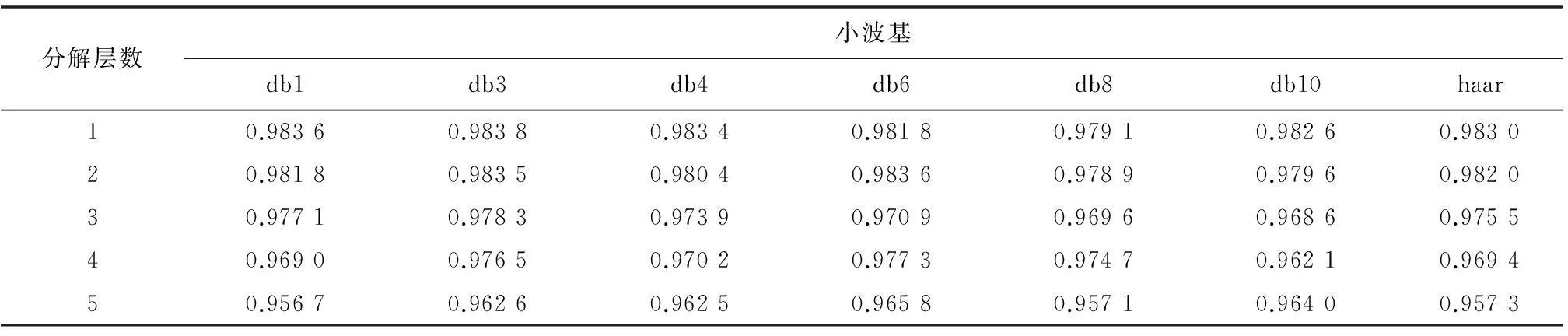
表1　　不同小波基在不同分解层数条件下分类正确率

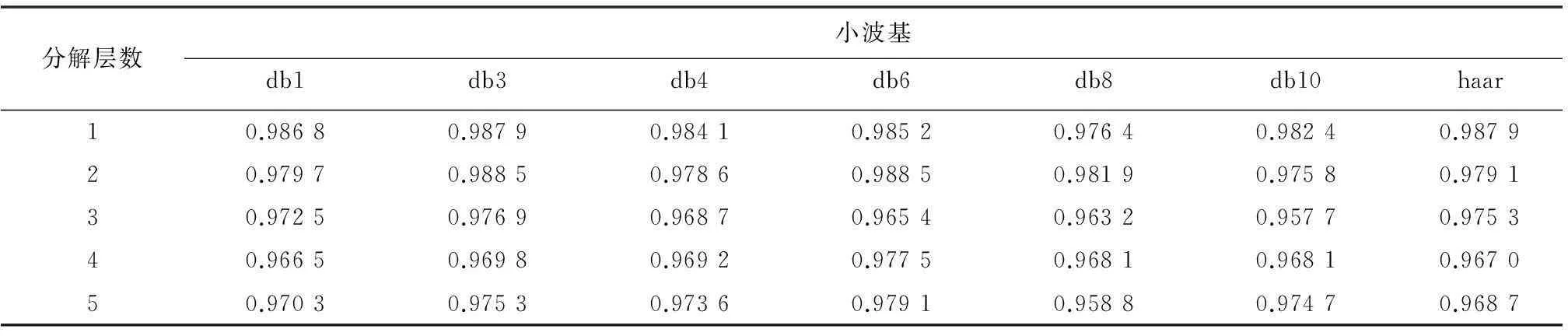
表2　不同小波基在不同分解层数条件下对应灵敏性

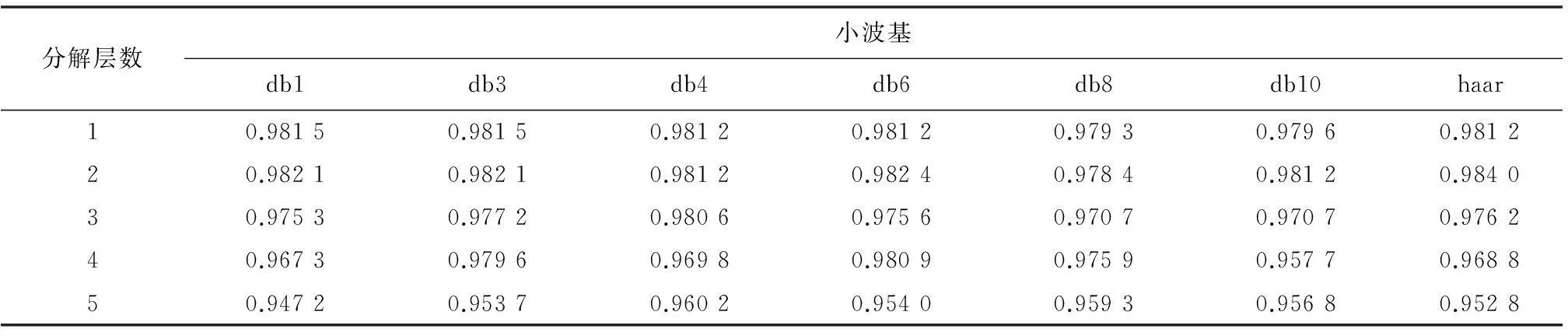
表3　不同小波基在不同分解层数条件下对应特异性

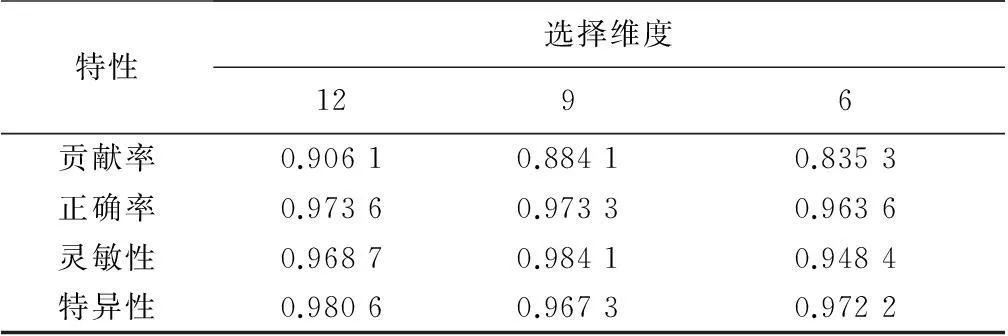
表4　不同维度数据在相同小波分解条件下结果

从表中数据，我们可以看出，随着维度数量的增加，正确率逐渐提高，但是当维度达到一定数量之后，正确率的增加量逐渐减小。

其他数据集同样经上述思路进行实验处理后，具体实验数据如下：

3.3.14/3/02数据集：

经实验处理后，本组数据前10维属性贡献率之和达到90.25%，分类实验取前10维如图7：

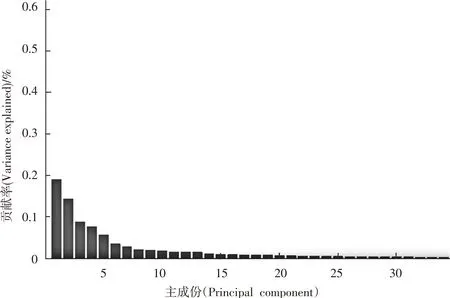
图7　4/3/02 数据集部分主要维度属性贡献率

注：前十维属性贡献率之和为90.25%。

Notes：Sum of the contribution rates of the first tenth properties is 90.25%.

由实验数据我们看到，对4/3/02 数据集进行实验，当使用db8小波基，小波分解层数为1时，其分类效果最佳：正确率86.45%，灵敏性87.00%，特异性85.90%。见表5、表6、表7。

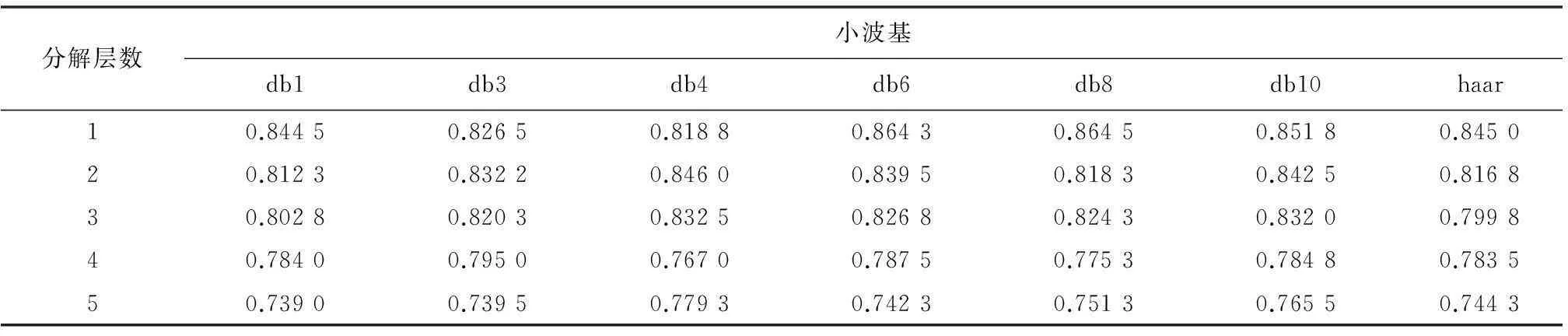
表5　不同小波基在不同分解层数条件下分类正确率(4/3/02数据集)

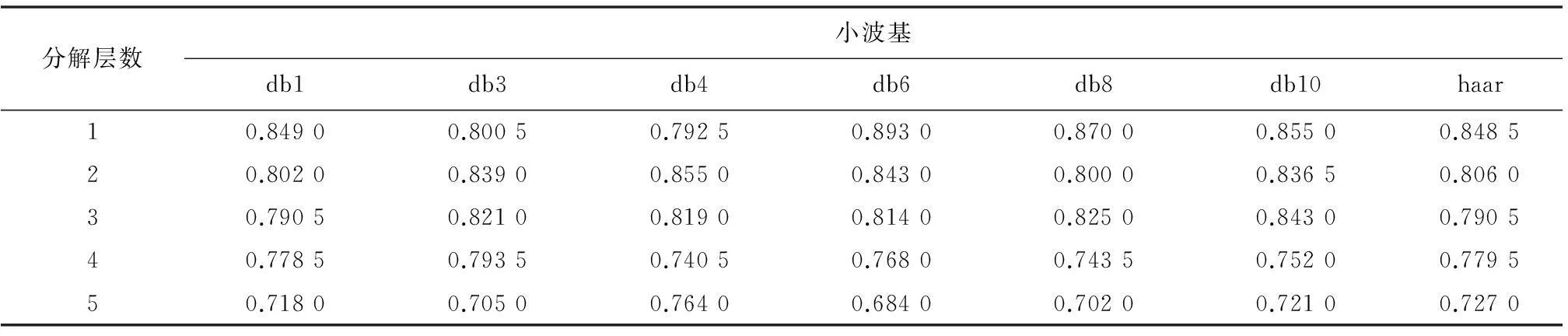
表6　不同小波基在不同分解层数条件下对应灵敏性(4/3/02数据集)

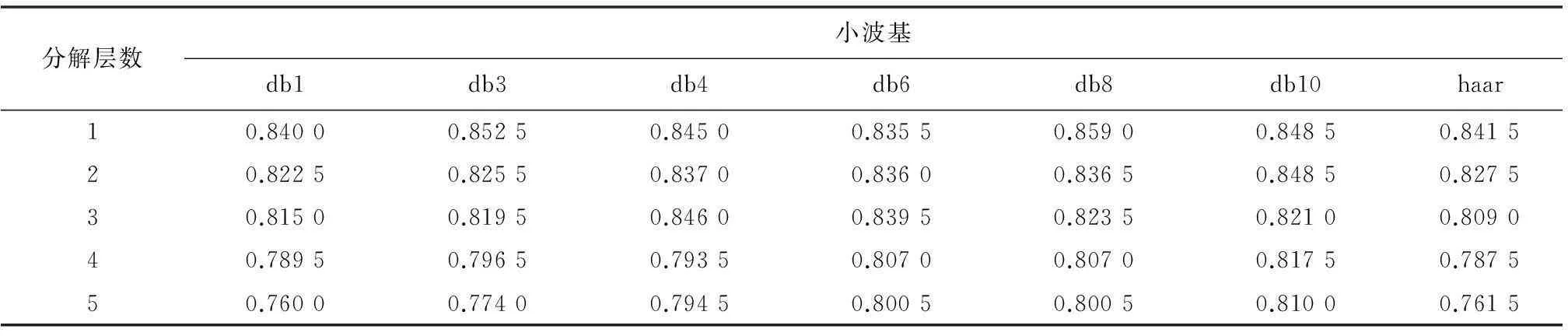
表7　不同小波基在不同分解层数条件下对应特异性(4/3/02数据集)

3.3.2OvarianCD_PostQAQC数据集

经实验处理后，本组数据前145维属性贡献率之和达到90.14%，分类实验取前145维，如图8：

由实验数据我们看到，对OvarianCD_PostQAQC数据集进行实验，当使用db10小波基，小波分解层数为3时，其分类效果最佳：正确率92.18%，灵敏性91.00%，特异性93.10%。见表8、表9、表10。

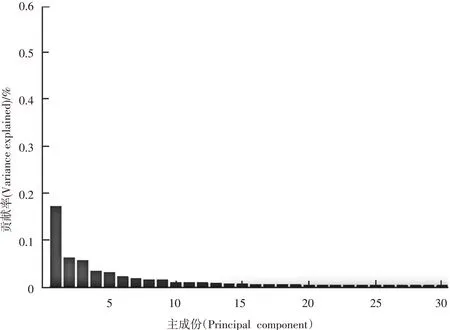
图8　OvarianCD_PostQAQC 数据集部分主要维度属性贡献率

注：前145维属性贡献率之和为90.14%。

Notes：Sum of the contribution rates of the first 145thproperties is 90.14%.

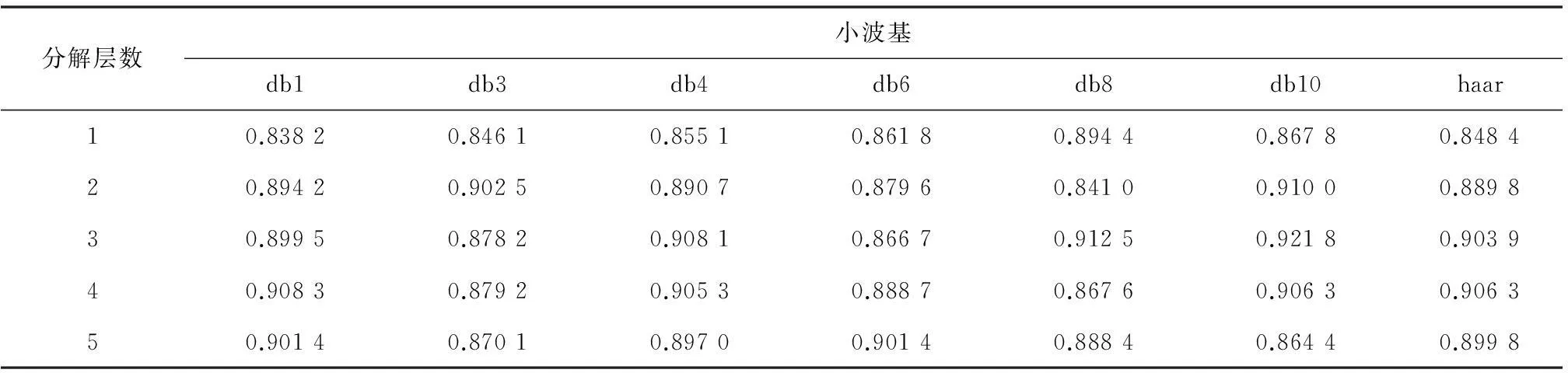
表8　不同小波基在不同分解层数条件下分类正确率(OvarianCD_PostQAQC数据集)

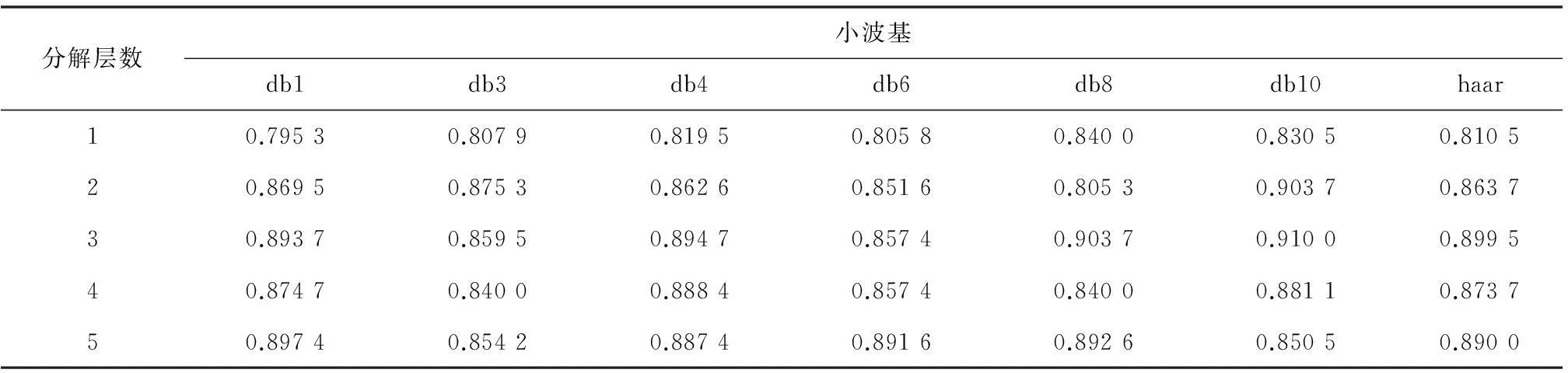
表9　不同小波基在不同分解层数条件下对应灵敏性(OvarianCD_PostQAQC数据集)

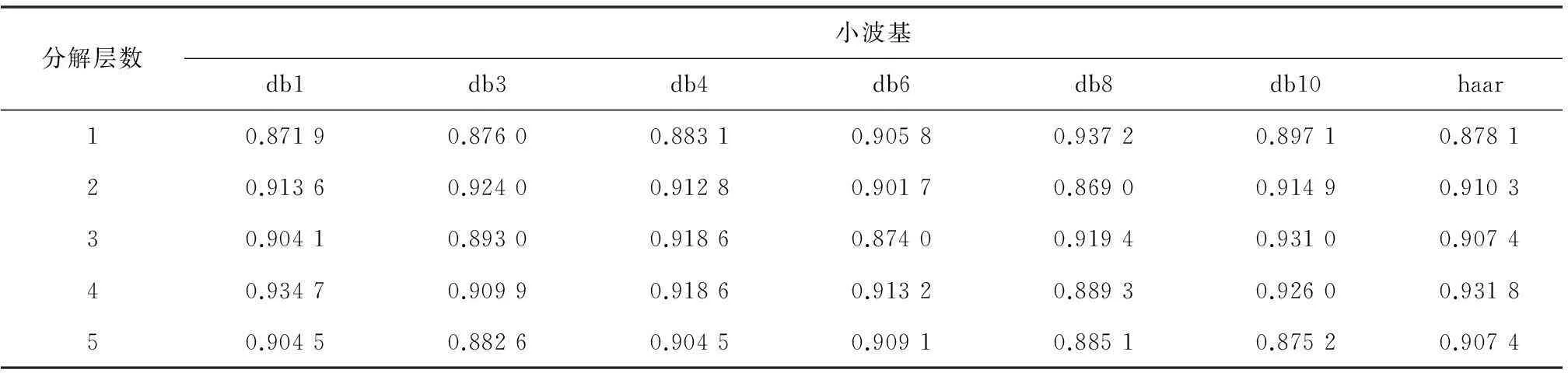
表10　不同小波基在不同分解层数条件下对应特异性(OvarianCD_PostQAQC 数据集)

4讨论与结论

经过一系列的实验，我们发现，同一组数据，在进行小波分解时，采用同一小波基，当分解层数不同时，分类结果会略有不同，如8-7-02数据集在使用db3小波基时，在一到五层分解时正确率分别为98.38%、98.35%、97.83%、97.65%、96.26%。另外，不同小波基，在相同分解层数条件下，对于数据分类结果，也会有不同影响，正确率会有所不同，但是差别不大，如8-7-02数据集在进行2层小波分解时，分别使用db1、db3、db4、db6、db8、db10、haar小波基时正确率分别为98.18%、98.35%、98.04%、98.36%、97.89%、97.96%、98.20%。与文献[4]的综合识别率基本持平，但是在数据处理中，通过小波分析和主成分分析大大降低了数据维度，简化了运算。

本文提出的模型中，先对蛋白质波谱数据进行小波分解，然后通过主成分分析提取特征，之后将特征送入支持向量机分类。经实验，本模型可以有效的降低数据计算量，提高效率，并能较好的对蛋白质波谱数据进行分类。

参考文献(References)

[1]吕红. 蛋白质质谱分析法的研究进展[J]. China Pharmacy, 2010, 21(25): 2388-2389.

LÜ Hong. The study progress of protein mass spectrometry analysis[J]. China Pharmacy, 2010, 21(25): 2388-2389.

[2]严勇, 王鑫, 杨慧中. 基于决策树与质谱分析数据的癌症判别[J]. 无锡职业技术学院学报, 2013, 12(1): 31-33.

YAN Yong, WANG Xin, YANG Huizhong. Cancer discriminant based on the decision tree and mass spectrometry analysis data[J]. Proceedings of the Wuxi Institute of Technology, 2013, 12(1): 31-33.

[3]SCHAPIRE R, FREUND Y, BARTLETT P, WEE SUN L. Boosting the margin:a new explanation for the effectiveness of voting methods[J]. The Annals of Statistics, 1988, 26(5): 1651-1686.

[4]邹修明, 罗楠, 孙怀江. 基于T检验与支持向量机的蛋白质质谱数据分析[J]. 淮阴师范学院学报(自然科学), 2011, 10(5): 409-413.

ZOU Xiuming, LUO Nan, SUN Huaijiang. Protein mass spectrometry analysis based on T-test and svm[J]. Proceedings of the Huaiyin Normal Univerity(natural sciences), 2011, 10(5): 409-413.

[5]杨合龙, 祝磊, 韩斌. 运用近邻传播聚类分析进行SELDI-TOF蛋白质谱特征选择[J]. 中国生物医学工程学报, 2013, 32(1): 14-18.

YANG Helong,ZHU Lei, HAN Bin. SELDI-TOF protein mass spectrometry feature selection based on neighbor clustering analysis[J]. Chinese Journal of Biomedical Engineering, 2013, 32(1): 14-18.

[6]KUEHL B, MARTEN S, BISCHOFF Y, et al. MALDI-ToF mass spectrometry-multivariate data analysis as a tool for classification of reactivation and non-culturable states of bacteria[J]. Anal Bioanal Chem, 2011, 401: 1593-1600.

[7]EBERLIN L, NORTON I, DILL A, et al. Classifying human brain tumors by lipid imaging with mass spectrometry[J]. Cancer Research, 2012, 72: 645-654.

[8]王昭鑫, 刘毅慧. 主元余像集主成分分析在蛋白质质谱数据中的应用[B]. 生物信息学, 2009, 7(3): 219-222.

WANG Zhaoxin, LIU Yihui. Application of 2nd PCA on protein mass spectrometry data[B]. Chinese Journal of Bioinformatics, 2009, 7(3): 219-222.

[9]BEHDAD M, FRENCH T, BARONE L, et al. On principal component analysis for high-dimensional XCSR[J]. Evolutionary Intelligence, 2012, 5(2): 129-138.

[10]Baldi P, Long A. A Bayesian framework for the analysis of microarray expression data:regularized t-test and statistical inferences of gene changes[J]. Bionformatics, 2001, 17: 509-519.

[11]ZHAO J. Asymptotic convergence of dimension reduction based boosting in classification[J]. Journal of Statistical Planning and Inference, 2013, 143(4): 651-662.

[12]李义峰, 刘毅慧. 基于遗传算法的蛋白质质谱数据特征选择[J]. 计算机工程, 2009, 35(19): 192-197.

LI Yifeng, LIU Yihui. Feature selection for protein mass spectrometry data based on genetic algorithm[J]. Computer Engineering, 2009, 35(19): 192-197.

[13]李义峰, 刘毅慧. 基于模拟退火算法的高分辨率蛋白质质谱数据特征选择[J]. 生物信息学, 2009, 2(7): 85-90.

LI Yifeng, LIU Yihui. Feature selection based on simulated annealing algorithm for high-resolutio protein mass spectrometry data[J]. Chinese Journal of Bioinformatics, 2009, 2(7): 85-90.

[14]LIU Yihui. Feature extraction and dimensionality reduction for mass spectrometry data[A]. Computers in Biology and Medicine, 2009, 39: 818-823.

[15]张德丰. MATLAB小波分析(第二版)[M]. 北京: 机械工业出版社, 2011.

ZHANG Defeng. The wavelet analysis of matlab(the second edition)[M]. Beijing: China Machine Press, 2011.

[16]GELADI P. Notes on the history and nature of partial least squares(PLS) modeling[J]. Journal of Chemometrics, 1988, 2: 231-246.

[17]边肇祺, 张学工. 模式识别(第二版)[M]. 北京：清华大学出版社, 2003.

BIAN Zhaoqi,ZHANG Xuegong. Pattern recognition(the second edition)[M]. Beijing: Tsinghua University Press, 2003.

[18]李义峰. 基于优化算法的蛋白质质谱数据分析[D]. 济南：山东轻工业学院, 2009.

LI Yifeng. Optimization algorithms based protein mass spectrometry data analysis[D]. Jinan: Shandong Polytechnic University, 2009.