利用位点特异性打分矩阵对大肠杆菌启动子的预测

利用位点特异性打分矩阵对大肠杆菌启动子的预测

闫妍，万平*

(首都师范大学生命科学学院，北京100048)

摘要：启动子是基因转录起始的一个关键性元件。本研究利用数据库中提供的大肠杆菌启动子数据，基于位点特异性打分矩阵(Position-specific scoring matrix，PSSM)算法建立了大肠杆菌启动子预测方法，并采用ROC曲线对预测结果进行评估。结果显示，本方法对大肠杆菌sigma24、sigma28、sigma32、sigma38、sigma54和sigma70启动子预测的准确度分别达到86%，96%，93%，96%，97%和74%。由于原核生物启动子序列的保守性，可将该方法推广至其他原核生物的启动子预测。

关键词：大肠杆菌；启动子；位点特异性打分矩阵(PSSM)；预测

中图分类号：Q811.4文献标志码：A

收稿日期：2015-01-14;修回日期：2015-03-10.

作者简介：吴文峰，男，硕士研究生，研究方向：智能信息及图像处理;E-mail:641178636@qq.com.

doi:10.3969/j.issn.1672-5565.2015.02.10

Prediction ofEscherichiacoliK-12 promoters using position-specific

scoring matrix (PSSM) method

YAN Yan, WAN Ping*

(CollegeofLifeScience,CapitalNormalUniversity,Beijing100048 ,China)

Abstract：Promoter is an essential element in transcription initiation. In this study, we proposed a method for the promoter prediction based on the position-specific scoring matrix(PSSM) constructed with the data from RegulonDB database,and evaluated the performance through the receiver operating characteristic(ROC).We predicted the Escherichia coli K-12 promoters, the accuracies of predictions for sigma24, sigma28, sigma32, sigma38, sigma54 and sigma70 are 86%, 96%, 93%, 96%, 97% and 74%, respectively. Since promoter sequences are conserved among prokaryotes, PSSM could be applied to the prediction of prokaryotic promoters.

Keywords：E.coli; Promoter; Position-specific Scoring matrix; Prediction

启动子是基因转录起始的一个关键性元件，位于基因转录起始点附近。在细菌中，启动子由RNA聚合酶核心酶与相应的sigma因子共同识别[1]。因子共有7种类型：sigma19、sigma24、sigma28、sigma32、sigma38、sigma54和sigma70，每种sigma因子所识别的序列都具有一定特征。除sigma54启动子外，启动子在转录起始位点上游-10和-35位附近都存在保守区域[2]；而sigma54启动子的保守区域位于转录起始位点上游-12和-24位附近[3]。

对于特征结构域建模的算法有很多。例如，常用的有位点特异性打分矩阵(Position-specific scoring matrix，PSSM，也称PWM)、贪婪算法、EM算法和MCMC算法，这些算法都有各自的优缺点[4]。此外，近年内也报导了一些新型算法，如pHMM-ANN方法[5]、GLECLUBS算法[6]、BOBRO算法[7-8]、神经网络算法[9]、构建非传统的16列双核苷酸矩阵的PSSM算法[10]。

在众多算法中，PSSM仍然是最常用的算法，占据重要的地位。PSSM在发现例如启动元件或可变剪接等具有信号核酸序列方面有着广泛的应用[11]。有很多构建PSSM的方法，最常用的就是使用排列好且长度相等的具有已知类似功能的结构域构建打分矩阵。这个打分矩阵的行数由结构域中的元素种类决定，列数则由结构域的元素个数决定。构建好的打分矩阵能够搜索DNA序列或蛋白序列中的与已知序列相似的序列[10]。

ROC曲线(Receiver operating characteristic curve)是一种坐标图式的分析工具，能描绘诊断中敏感性和特异性之间的制约关系[12]。

目前还未见采用PSSM方法预测原核生物启动子的报道。本研究采用PSSM方法预测大肠杆菌启动子，并且通过ROC曲线评估预测结果。

1数据和方法

1.1大肠杆菌K-12启动子核酸序列

大肠杆菌K-12 sigma24、sigma28、sigma32、sigma38、sigma54和sigma70启动子的核酸序列下载自RegulonDB数据库(http://regulondb.ccg.unam.mx/)。RegulonDB收录了大肠杆菌K-12各种转录起始时的调控复合体和调控网络。除此之外，它还包括了各种功能的基因间的相互作用，如转录复合体、操纵子以及简单或复杂的调控子的基因[13]。

由于sigma19启动子在RegulonDB中只有一条序列，未列入本研究。对于下载的启动子序列，我们先对数据进行筛选。筛选包括去掉数据库中的冗余序列、无注释信息序列、以及属于多类启动子的序列。属于多类启动子的序列指可同时被多类启动子识别的序列，这些序列会影响PSSM的预测效果。经过筛选处理后，共得到2 954条启动子序列，其中sigma24有511条，sigma28有138条，sigma32有285条，sigma38有130条，sigma54有92条、sigma70有1 787条。

1.2位点特异性打分矩阵(PSSM)的构建

对大肠杆菌K-12的每类启动子，分别构建位点特异性打分矩阵(PSSM)。

1.2.1构建频数矩阵

从RegulonDB下载的启动子序列每一条的长度都为81个碱基。以DNA序列上的基因翻译起始点的碱基位置定为0，将其坐标化，则启动子全长即为-60~20。构建频数矩阵时，首先要统计每个坐标位置中4种核苷酸出现的次数，将结果填入4行81列矩阵中。该矩阵行的名称分别为A、C、G、T，列名为启动子对应的位置坐标值。

1.2.2构建伪计数矩阵

频数矩阵的某些元素的值可能为0。一般认为，这是由于收集数据时的数据量不足造成的。为弥补这一缺陷，通常对频数矩阵中每个元素的值加一个正数(本研究中加1)，生成伪计数矩阵(Peudo count matrix)。

1.2.3构建概率矩阵

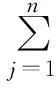
(1)

1.2.4构建几率比(Odds ratio)矩阵

将概率矩阵中每个元素的值除以所对应的碱基在随机条件下出现的概率(均为0.25)，即得到几率比(Odds ratio)矩阵。如公式(2)所示，其中M代表实际观测情况，R代表随机情况。

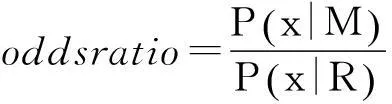
(2)

1.2.5构建对数几率比(Log-Odds ratio)矩阵，即位点特异性打分矩阵(PSSM)

将几率比矩阵中的每个元素取以2为底的对数，再取整数部分，即得到对数几率比矩阵(公式(3))，这就是最终的位点特异性打分矩阵(PSSM)。

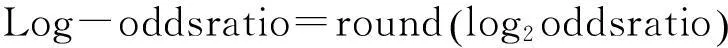
(3)

1.3利用PSSM预测大肠杆菌K-12的启动子

1.3.1预测方法

对于给定的DNA序列，根据每个位置上出现的碱基，在PSSM中查出相应的得分，然后对各个位置的得分求和，得到总分。采用不同启动子的PSSM分别对同一DNA序列打分，得分最高者被视为此DNA序列所属的启动子类型。

1.3.2分别对阳性数据集和阴性数据集进行预测

对于特定的启动子类型，阳性数据集指属于该类启动子的DNA序列，阴性数据集指不属于该类启动子的DNA序列。本研究中，阳性数据集和阴性数据集所包含的序列数目为1∶1。阴性数据集由不属于某类启动子的其它5类启动子序列组成。

1.4利用ROC曲线对预测结果进行评估

使用RStudio中的ROCR包[14]绘制ROC曲线。

ROC曲线中，AUC代表“曲线下面积”，该值越趋近1，说明预测效果越好。

敏感度(Sensitivity, Sens)、特异性(Specificity, Spec)和准确度(Accuracy, Acc)评估预测效果[15]。公式(4)~(6)，式中TP为真阳性，FN为假阴性，TN为真阴性，FP为假阳性。

(4)

(5)

(6)

2结果

2.1大肠杆菌K-12 6种启动子的PSSM

我们计算了大肠杆菌K-12的6种启动子的PSSM图1是6类启动子相应的logo。为做ROC评估提供阳性数据集和阴性数据集，采用如下方法处理E.coliK-12启动子的perl脚本：

#!/usr/bin/perl-w

use strict;

#从RegulonDB上下载的启动子的原始数据放在一个文件夹下

my @file=glob"PromoterSigma*Set.txt";

my (%sigma_all_sequences, %matrices_total, %prediction_all);

# Score Matrices Computation

foreach my $file(@file){

my ($promoter_index) = $file =~ /PromoterSigma(.*)Set.txt/;

my (%sigma_sequences, %sigma_transposition_sequences);

my ($score, @matrix_score);

# Store the promoters of current file into %sigma_sequences and then

# store all types of the promoter sequences into %sigma_all_sequences.

open(DATA,$file)||die"Can't open file "$file"! ";

while(){

chomp;

(/^#/ or /^s*$/) and next;

my @fields = split(" ");

($fields[5]!~/^[acgtACGT]+$/ or $fields[4]=~/,/) and next;

$sigma_sequences{lc($fields[5])}=$fields[4];

}

$sigma_all_sequences{$promoter_index}=\%sigma_sequences;

# Transposit the %sigma_sequences to %sigma_transposition_sequences

# in order to calculate the score matrices.

foreach my $key(keys %sigma_sequences){

my @fields=split("",$key);

for(my $i=0; $i<@fields; $i++){

$sigma_transposition_sequences{$i}.=$fields[$i];

}

}

# Calculate score matrices and store the results in %matrices_total.

foreach my $key(sort {$a <=> $b}keys %sigma_transposition_sequences){

my $promoter_num=length$sigma_transposition_sequences{$key};

my @fields=split("",$sigma_transposition_sequences{$key});

my %acgt=();

foreach my $base(@fields){

(exists $acgt{$base}) ? ($acgt{$base}++) : ($acgt{$base}=1);}

foreach my $base(keys %acgt){

my $base_score = ($acgt{$base}+.1)*4/($promoter_num+.4);

$base_score = sprintf"%.0f", log($base_score)/log(2);

$matrix_score[$key][judge($base)] = int($base_score);

}

}

$matrices_total{$promoter_index}=@matrix_score;

}

# True or False Promoters Prediction

foreach my $file(@file){

my ($promoter_index) = $file =~ /PromoterSigma(.*)Set.txt/;

my %prediction;

# True promoters score

foreach my $key(keys%{$sigma_all_sequences{$promoter_index}}){

my $score;

for(my $i = 0; $i < length$key; $i++){

$score += ${$matrices_total{$promoter_index}}[$i][judge(substr($key, $i, 1))];

}

$prediction{$key}=$score." T";

}

# False promoters score

foreach my $key(keys %sigma_all_sequences){

$key =~ $promoter_index and next;

foreach my $false_key(keys %{$sigma_all_sequences{$key}}){

my $score;

for(my $i = 0; $i < length$false_key; $i++){

$score += ${$matrices_total{$promoter_index}}[$i][judge(substr($false_key, $i, 1))];

}

$prediction{$false_key}=$score." F";

}

}

$prediction_all{$promoter_index}=\%prediction;

}

# Print the score into files.

foreach my $key(keys %prediction_all){

open(RS,">score_sigma".$key.".txt");

foreach my $sub_key(keys %{$prediction_all{$key}}){

print RS $sub_key," ",${$prediction_all{$key}}{$sub_key}," ";

}

close RS;

}

sub judge{

my($string)=@_;

my $num;

$string=~/a/ and $num=0;

$string=~/c/ and $num=1;

$string=~/g/ and $num=2;

$string=~/t/ and $num=3;

return $num;

}

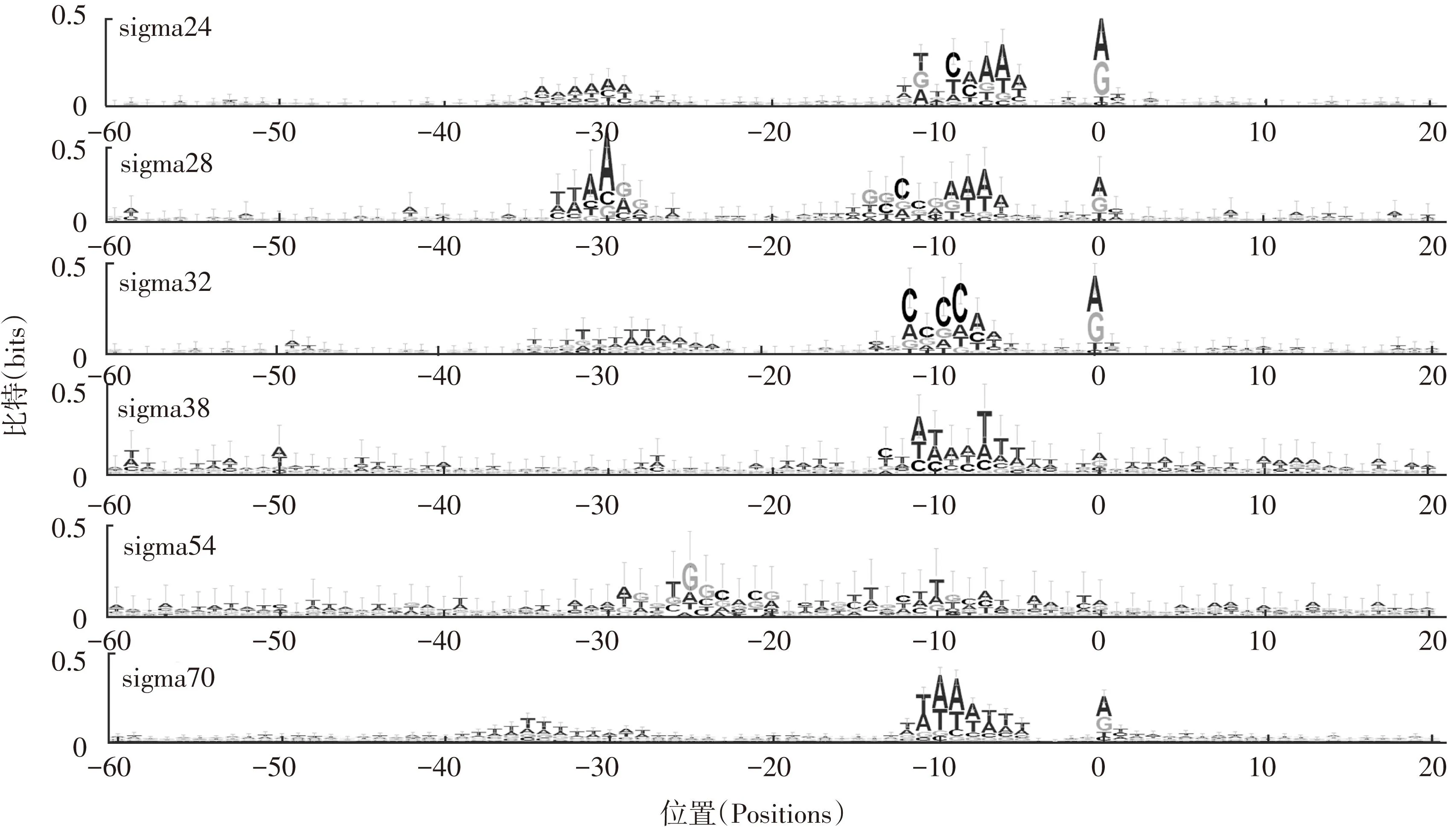
图1　大肠杆菌K-12 6种启动子的Logo

3.2ROC曲线

根据对6种启动子预测结果，我们使用R语言的ROCR包绘制了相应的ROC曲线(图2)。表1显示了PSSM对每一种启动子预测的敏感度(Sensitivity)和特异性(Specificity)。绘制ROC曲线的Rscript如下：

library(ROCR)

setwd("") # 将工作目录设在原始数据在的地方

par(mfrow=c(2,3),bg="white",mai=c(.6,.6,.6,.6))

for(i in c("24","28","32","38","54","70")){

data=read.table(paste0("score_sigma",i,".txt"))

pred <- prediction(data[,2],data[,3])

perf <- performance(pred,"tpr","fpr")

sens <- performance(pred,"spec","sens")@x.values

spec <- performance(pred,"spec","sens")@y.values

print(paste0("sigma",i,sens,spec))

auc <- format(performance(pred,"auc")@y.values,digits=2)

plot(perf,main=paste0("sigma",i),colorize=FALSE,lwd=2,xaxis.cex.axis=1,

yaxis.cex.axis=1,yaxis.las=1,cex.main=1.5)

segments(0,0,1,1,lty=2)

text(0.6,0.5,paste0("AUC=",auc),cex=1.2)

}

σ24σ28σ32σ38σ54σ70Sensitivity0.710.930.740.740.730.73Specificity0.840.740.880.640.770.68

4讨论

通过比较PSSM与BacPP方法[16]的准确度(Acc)(见表2)可以看出，PSSM方法在预测6种类型的sigma因子时，有3种启动子(sigma28、sigma32、sigma38)的预测准确度优于BacPP方法；一种启动子(sigma54)的预测准确度与BacPP方法持平，均为0.97。

表2　PSSM与BacPP方法的准确度(Acc)比较

从结果我们可以判断，用PSSM模型预测原核生物启动子是一种较为准确的算法。

首先，图1中的ROC曲线都处于坐标对角虚线的上方，这说明使用PSSM预测启动子的概率比随机概率要高。

其次，根据AUC的值判断PSSM方法的可信性。图中的AUCs只有sigma38为0.74，其余均大于0.8，说明PSSM的可信度很高。

再次，预测方法的敏感性和特异性是评价一种预测方法最具说明力的指标。在表1中，PSSM的敏感性和特异性均大于0.6。另外，sigma28的敏感性达到了0.93，达到了相当高的水平。

PSSM算法为大肠杆菌K-12启动子的预测提供了一种较为准确的可靠方法。从ROC曲线的形状、AUC值，以及敏感度、特异性和准确度值均表明PSSM在预测启动子方面的有效性。由于原核生物的启动子具有较大的保守性，PSSM可以作为原核生物启动子预测的一种有效方法。PSSM方法缺陷在于，使用PSSM方法需要指定打分矩阵的窗口大小，该缺陷可以通过采用隐马尔科夫模型(HMM)方法得以克服。另外，我们还将采用多重交叉验证的方法进一步提高预测的准确度。

参考文献(References)

[1]杨明，李权胜．原核生物的sigma因子[J]．河南医学研究，1999，8(1)：88-90．

YANG Ming，LI Quansheng．Prokaryotic sigma factors [J]．Henan medical research，1999，8(1)：88-90．

[2]HAWLEY D K , MCCLURE W R．Compilation and analysis of Escherichia coli promoter DNA sequences[J]．Nucleic Acids Rresearch，1983，11(8)：2237-2255．

[3]THÖNY B, HENNECKE H．The -24/-12 promoter comes of age [J]．FEMS Microbiol. Rev，1989，63：341-357．

[4]GUHATHAKURTA D．Computational identification of transcriptional regulatory elements in DNA sequence [J]．Nucleic Acids Research，2006，34(12)：3585-3598．

[5]MANN S，LI J，CHEN Y P P．A pHMM-ANN based discriminative approach to promoter identification in prokaryote genomic contexts[J]．Nucleic Acids Res，2007，35：e12．

[6]ZHANG S，XU M，LI S，et al．Genome-wide de novo prediction of cis-regulatory binding sites in prokaryotes[J]．Nucleic Acids Research，2009，37(10)：e72．

[7]LI G，LIU B，MA Q，et al．A new framework for identifying cis-regulatory motifs in prokaryotes[J]．Nucleic Acids Research，2011，39(7)：e42．

[8]MA Q，LIU B，ZHOU C，et al．An integrated toolkit for accurate prediction and analysis of cis-regulatory motifs at a genome scale[J]．Bioinformatics，2013，29(18)：2261-2268．

[9]AHMAD S，SARAI A．PSSM-based prediction of DNA binding sites in proteins[J]．BMC Bioinformatics，2005，6：33．

[10]GERSHENZON N I，STORMO G D，IOSHIKHES I P．Computational technique for improvement of the position-weight matrices for the DNA/protein binding sites[J]．Nucleic Acids Research，2005，33(7)：2290-2301．

[11]CLAVERIE J M，AUDIC S．The statistical significance of nucleotide position-weight matrix matches[J]．Computer Applications in the Biosciences，1996，12(5)：431-439．

[12]韦修喜，周永权．基于ROC曲线的两类分类问题性能评估方法[J]．计算机技术与发展，2010，20(11)：47-50．

WEI Xiuxi，ZHOU Yongquan．Assess of performance of two types of classification methods based on ROS[J]．Computer Technology and Development，2010，20(11)：47 -50．

[13]SALGADO H，PERALTA-GIL M，GAMA-CASTRO S， et al．RegulonDB(version 8.0)： Omics data sets，evolutionary conservation，regulatory phrases，cross-validated gold standards and more[J]．Nucleic Acids Research，2012，41(D1)：D203-213．

[14]SING T，SANDER O，BEERENWINKEL N，et al．ROCR: visualizing classifier performance in R[J]．Bioinformatics，2005，21(20)：7881．

[15]ZHOU X，LI Z，DAI Z，et al．Predicting promoters by pseudo-trinucleotide compositions based on discrete wavelets transform[J]．Journal of Theoretical Biology，2013，319：1-7．

[16]DE AVILA E SILVA S，ECHEVERRIGARAY S，GERHARDT G J．BacPP： bacterial promoter prediction-a tool for accurate sigma-factor specific assignment in enterobacteria[J]．J.Theor Biol,2011，287：92-99．

*通信作者：刘毅慧, 女, 博士, 教授,研究方向: 生物计算, 智能信息处理等;E-mail:yxl@sdili.edu.cn.