α-最大相容水平SF决策信息系统的知识约简

罗　胜，林福宁

(1.西安交通大学经济与金融学院，中国 西安　710049;2.广西财经学院工商管理学院，中国 南宁　530003)

α-最大相容水平SF决策信息系统的知识约简

罗胜1*，林福宁2

(1.西安交通大学经济与金融学院，中国 西安710049;2.广西财经学院工商管理学院，中国 南宁530003)

摘要引入了SF决策信息系统中的最大相容水平概念，研究了α-最大相容水平ε-不协调SF决策信息系统，建立了它的粗糙集模型，讨论了它的α-水平分布ε-约简.

关键词SF决策信息系统；α-最大相容水平；ε-不协调；α-水平分布ε-约简

Knowledge Reductions ofα-Maximal Tolerance Level

SF Decision Information Systems

LUOSheng1*,LINFu-ning2

(1.School of Economics and Finance, Xi’an Jiaotong University, Xi’an 710049, China;

2.School of Business Administration, Guangxi University of Finance and Economics, Nanning 530003, China)

AbstractThe concept of maximal tolerance levels in SF decision information systems is introduced, theα-maximal tolerance level andε-inconsistent SF decision information systems are reached, its rough set model is established and itsα-level distributionε-reductions are discussed.

Key wordsSF decision information system;α-maximal tolerance level;ε-inconsistent;α-level distributionε-reduction

粗糙集理论[1]由著名科学家Pawlak在1982年提出，它是处理信息系统的有力工具，在医疗诊断、数据挖掘、模式识别以及知识发现[2]等方面应用广泛.

集值信息系统作为一种重要的信息系统，近年来得到了深入研究.王虹等[3]与宋笑雪等[4]研究了基于相容关系的集值信息系统.但相容类有一些不足，管延勇等[5]为此引入了最大相容类的概念，弥补了一般相容类所存在的不足.此外，最大相容类的思想也被陈子春等[6]、陈秀等[7]应用于各自提出的变精度相容关系下的集值信息系统.这些成果说明通过最大相容类来研究集值信息系统的约简问题是可行的.

模糊决策信息系统是模糊环境下的决策信息系统.关于决策信息系统和模糊决策信息系统的研究，目前已有不少成果产生，如Zhou等[8]绘出了决策信息的相对约简的快速算法；Luo等[9]研究了集值序决策信息系统中近似的动态保持；Zhang等[10]则研究了区间值决策信息系统中多信规则的获取和信赖保持属性约简；如管涛等[11]提出了基于模糊决策信息系统的粗糙分布约简等若干类约简，刻画了其相关性质与约简判定定理；余承依[12]等研究了不协调决策信息系统最大分布约简新方法；黄兵等[13]研究了模糊决策信息系统的变精度粗糙集模型；杨习贝等[14]通过建立一种基于参数分类的自反关系，将集值信息系统引入模糊环境中讨论.喻光继[15]研究了区间值模糊决策信息系统的属性约简.

集值模糊决策信息系统(简称SF决策信息系统)则是模糊环境下的集值决策信息系统，α-最大相容水平SF决策信息系统是它的推广.本文深入研究了α-最大相容水平SF决策信息系统的知识约简，从而以上提到的SF决策信息系统的知识约简是它的特款.

1基本概念

在本文中，集值模糊决策的信息系统简称SF决策信息系统，U表示称为论域的非空集.2U表示U的幂集，I表示闭区[0，1]，BA表示所有由集A到集B的映射构成的集.为了方便，约定

U={x1,x2,…,xn},A={a1,a2,…,am},D={d1,d2,…,dp},ε∈[0,1].

定义1.2[9]称(U,A,F,D,G)为SF决策信息系统，其中(U,A,F)为集值信息系统，即U为对象集，A为条件属性集，F={fa∈(2Va-{∅})U:a∈A}为U与A的关系集，fa称为a的信息函数，Va为a的值域；D称为决策属性集；G={gd∈IU:d∈D}为U与D的关系集，U上的模糊集gd称为d的信息函数.

定义1.3[2]设(U，A，F，D，G)为SF决策信息系统.令

RA={(xi,xj):fal(xi)=fal(xj)(∀l≤m)},RD={(xi,xj):gdk(xi)=gdk(xj)(∀k≤p)}.

若RA⊆RD,则称(U,A,F,D,G)为协调SF决策信息系统；否则，称(U,A,F,D,G)为不协调SF决策信息系统.

SF决策信息系统中对象关于条件属性的信息函数值未必是单值的，若按等价关系来处理分类问题，会出现划分过细的情况，不便于提取知识.为此考虑相容关系.

定义1.4[5]设R为U上的相容关系.

(1) 称X∈2U为U上的R相容类，若对∀x,y∈X,有xRy.

(2) 称X∈2U为U上的R最大相容类，若X为U上的R相容类，且对∀x∈U-X,存在y∈X使(x,y)∉R.

不同相容类之间可能存在包含关系，不能保证同一相容类中的对象之间两两相容.针对这些不足，可考虑最大相容类.最大相容类之间不存在包含关系，只可能有相交关系，这样保证了同一类中的元素的“共性”没有被丢失.

让U上的所有R最大相容类构成的集为CCR(U).对x∈U,记

CCR(x)={K∈CCR(U):x∈K},

它表示U上的所有包含x的R最大相容类构成的集.

定义1.5[3-4]设(U,A,F,D,G)为SF决策信息系统，对∀B⊆A,定义U上的关于B的相容关系TB如下：

TB={(x,y)∈U×U:fb(x)∩fb(y)≠∅(∀b∈B)}.

对∀x,y∈U,若xTBy,则称x,y关于B是相容的.记TB(x)={y∈U:xTBy}.

对b∈B,x∈U,简记

Tb=T{b},Tb(x)=T{b}(x);

CCTb(U)=CCT{b}(U),CCTb(x)=CCT{b}(x).

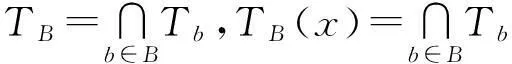
定义1.6[10]设(U,A,F,D,G)为SF决策信息系统，对∀xi,xj∈U,定义

SD(xi,xj)=∧{1-|fd(xi)-fd(xj)|:d∈D},

其中fd(xi)表示xi关于决策属性d的信息函数值：

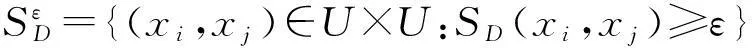
其中ε称为(U,A,F,D,G)的决策容差.

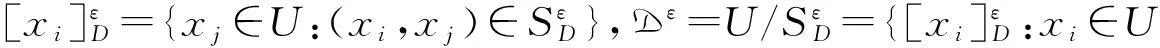
2最大相容水平与ε-不协调SF决策信息系统

在SF决策信息系统中引入最大相容水平概念，以此定义一种具有变精度的相容关系.

定义2.1[10]设(U,A,F,D,G)为SF决策信息系统.对xi,xj∈U,b∈B⊆A,α∈[0,1],记

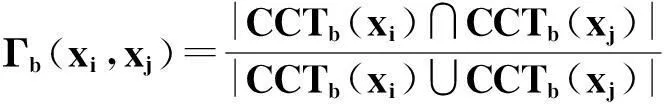
其中|·|表示集的基数，CCTb(xi)∩CCTb(xj)={S∈2U:S∈CCTb(xi)且S∈CCTb(xj)},CCTb(xi)∪CCTb(xj)={S∈2U:S∈CCTb(xi)或S∈CCTb(xj)}.记

与xi,xj∈U的最大相容类相关的二元函数Γb(xi,xj)依赖α的值，则称α为(U,A,F,D,G)的最大相容水平，称(U,A,F,D,G)为α-最大相容水平SF决策信息系统.

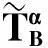
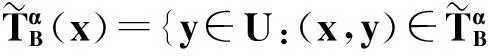
性质2.1对x∈U,C⊆B⊆A与α∈[0,1],有

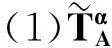
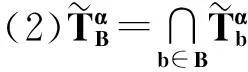
证显然.

显然，不协调SF决策信息系统是1-最大相容水平1-不协调SF决策信息系统的特例，协调SF决策信息系统则是1-最大相容水平1-协调SF决策信息系统的特例.

表1　SF决策信息系统(U,A,F,D,G)

3知识约简

定义3.1设(U,A,F,D,G)为α-最大相容水平SF决策信息系统.对B⊆A,X∈2U,定义

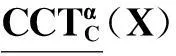
证由性质3.1可证.

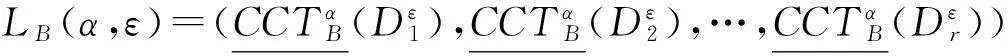
它们分别称为α水平下分布函数和α-水平上分布函数.

(1)若LB(α,ε)=LA(α,ε),则称B为α水平下ε-分布协调集；若还满足对∀B′B,有LB′(α,ε)≠LA(α,ε),则称B为α-水平下分布ε-约简.

(2)若HB(α,ε)=HA(α,ε),则称B为α水平上ε-分布协调集；若还满足对∀B′B,有HB′(α,ε)≠HA(α,ε),则称B为α-水平上分布ε-约简.

对x∈U,α∈[0,1],记

命题3.1设(U,A,F,D,G)为α-最大相容水平ε-不协调SF决策信息系统，U的模糊决策分类为Dε.

证显然.

定理3.1设(U,A,F,D,G)为α-最大相容水平ε-不协调SF决策信息系统，B⊆A,则下列条件等价：

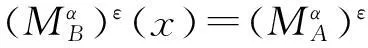
证(1)对U的模糊决策分类Dε,

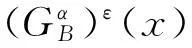
故B为α-水平下分布ε-协调集当且仅当

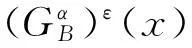
(2)类似(1)可证.

定义3.3设(U,A,F,D,G)为α-最大相容水平ε-不协调SF决策信息系统，B⊆A,U的模糊决策分类为Dε.对∀xi,xj∈U,记

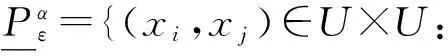
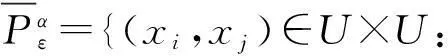
定义

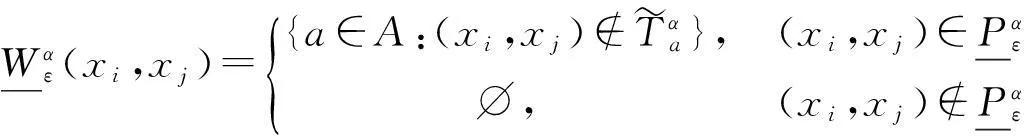
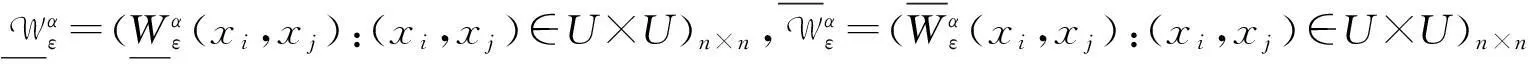
定理3.2设(U,A,F,D,G)为α-最大相容水平ε-不协调SF决策信息系统，B⊆A,则对∀xi,xj∈U,有：

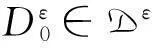
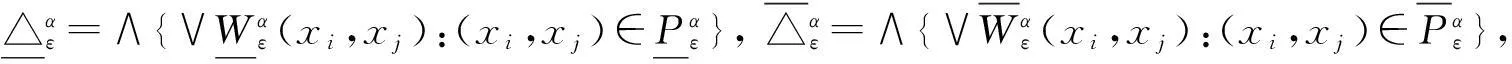
它们分别称为(U,A,F,D,G)的α-水平下、上分布ε-区分辨识函数.

定理3.3设(U,A,F,D,G)为α-最大相容水平ε-不协调SF决策信息系统，其α-水平下、上分布ε-区分辨识函数的极小析取范式分别为

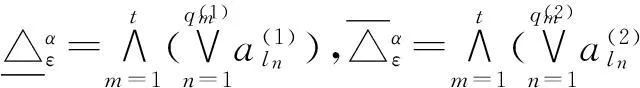
记

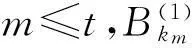
证利用布尔推理定理可证.

例3.1考虑例2.1中的0.4-最大相容水平0.7-不协调SF决策信息系统(U,A,F,D,G).它的0.4-水平下分布0.7-区分辨识属性矩阵为：

它的0.4-水平下分布0.7-区分函数：

因此B={a2,a3}为它的0.4水平下分布0.7-约简.

4结语

本文介绍了最大相容水平概念，基于它定义了变精度相容关系，给出了α-最大相容水平ε-不协调SF决策信息系统.

参考文献：

[1]PAWLAK Z. Rough sets [J]. Int J Comput Inf, 1982,11(5):341-356.

[2]张文修，梁怡，吴伟志.信息系统与知识发现[M].北京：科学出版社, 2003.

[3]王虹，张文修，李鸿儒.集值信息系统的知识发现与约简[J].计算机工程与应用, 2005,40(6):37-38.

[4]宋笑雪，解争龙，张文修.集值决策信息系统的知识约简与规则提取[J].计算机科学， 2007,34(4):182-191.

[5]管延勇，王洪凯，史开泉.集值信息系统及其属性约简[J].数学的实践与认识, 2008,28(2):101-107.

[6]陈子春，秦春云.集值信息系统基于变精度相容关系的知识约简[J].计算机工程与应用, 2008,44(9):27-29.

[7]陈秀，李克典.集值决策信息系统及其知识约简[J].海南师范大学自然科学学报, 2008,21(4):389-392.

[8]ZOU H, ZHANG C. Quick algorithm for relative reduction based on decision information system [J].Procedia Eng, 2011,15(5):1504-1508.

[9]LUO C, LI T, CHEN H. Dynamic maintenance of approximations in set-valued ordered decision systems under the attribute generalization [J]. Inf Sci, 2014,257(4):210-228.

[10]ZHANG X, MEI C, CHEN D,etal. Multi-confidence rule acquisition and confidence-preserved attribute reduction in interval-valued decision systems [J]. Int J Approxim Reasoning, 2014,55(8):1787-1804.

[11]管涛，冯博琴.模糊目标信息系统上的知识约简方法[J].软件学报, 2004,15(10):1470-1478.

[12]余承依，李进金.不协调决策信息系统最大分布约简新方法[J].计算机应用, 2011,31(6):1645-1648.

[13]黄兵，周献中，胡作进.模糊目标信息系统的VPRS模型及知识约简[J].系统工程与电子技术， 2007,29(11):1859-1862.

[14]杨习贝，杨静宇，吴陈.模糊集值信息系统中的决策规则获取研究[J].系统仿真学报, 2008,20(5):1199-1202.

[15]喻光继. IVED信息系统的属性约简的一个注记[J].湖南师范大学自然科学学报, 2014,37(4):66-71.

(编辑陈笑梅)

*通讯作者,E-mail：shengluo100@126.com

基金项目：国家社会科学基金资助项目(12BJL087)

收稿日期：2014-06-23

中图分类号TP18

文献标识码A

文章编号1000-2537(2015)03-0063-06

DOI:10.7612/j.issn.1000-2537.2015.03.012