基于粗糙集的可变正区域约简

邓大勇，　李亚楠，　薛欢欢

(1.浙江师范大学 数理与信息工程学院,浙江 金华　321004;2.浙江师范大学 行知学院,浙江 金华　321004)



基于粗糙集的可变正区域约简

邓大勇1，2，李亚楠1，薛欢欢1

(1.浙江师范大学 数理与信息工程学院,浙江 金华321004;2.浙江师范大学 行知学院,浙江 金华321004)

属性约简是粗糙集理论的研究重点之一.现有的各种粗糙集约简几乎都是保持某种约简准则不变，用这种方法处理一些存在异常点的数据时,在泛化能力方面存在一定的问题.针对此类问题,提出了一种可变正区域的约简方法,该方法在进行属性约简时允许正区域存在一定程度的变化.理论分析和示例表明了该方法的有效性.

粗糙集;属性约简;可变正区域;异常点;属性重要性

0　引　言

粗糙集理论[1-3]的主要优势是属性约简和不确定性分析，而且不需要先验知识,直接能从数据中抽取所需的知识.已经有很多粗糙集的扩展模型，包括：可变精度粗糙集[4-5]、概率粗糙集[6-8]、覆盖粗糙集[9-11]、领域粗糙集[12-14]、决策粗糙集[15-17]、F-粗糙集[18-19]等.这些粗糙集模型能够处理不同类型的数据，它们都有自己的约简方法和约简准则.例如，Pawlak约简[1-3]、基于互信息的约简[20]、基于条件熵的约简[21-22]、并行约简[18-19]等.几乎所有的粗糙集约简都是保持某种约简准则不变，并宣称保持分类信息不变.然而，这些约简准则都显得不够灵活，难以处理复杂多变的数据并适应各种要求.

可变精度粗糙集是为了去除数据集中的噪音干扰,放大数据的正区域，同时也导致了正区域与条件属性之间并不一定存在单调关系,给属性约简造成了一定的困难.对于与异常点相关的问题也难以处理.

例如:现实生活中,有少量的人非常有个性、非常有特点，利用这些个性或特征区分这个人与其他人非常有效.用粗糙集的语言描述，这种个性或特征就是核属性.但是这种个性、特征或所谓的核属性几乎没有泛化能力，也就是说，对于区分其他个体不仅不利反而有害.

如何处理类似的问题？对目前的粗糙集理论来说，似乎缺乏行之有效的方法.本文提出一种可变正区域的约简方法，该方法在处理此类问题时比较有效.可变正区域的约简方法在约简过程中并不严格保持正区域不变，而是允许正区域在一定的范围内发生变化，从而约简掉给泛化能力造成一定困难的少部分属性，甚至是核属性，从而提高泛化能力和分类准确率.

1　基础知识

本节简单介绍粗糙集[1-3]的基本知识.

设IS=(U,A)是一个信息系统，其中U是论域，A是论域U上的条件属性集.对于每个属性a∈A,都对应着一个函数a(x):U→Va，称Va为属性a的值域，称U中每个元素为个体、对象或行.

对于每一个属性子集B⊆A和任何个体x∈U，都对应着一个如下的信息函数：

B-不分明关系定义为

任何满足关系IND(B)的2个元素x，y都不能由B的属性子集区分，[x]B表示由x引导的IND(B)等价类.

对于信息系统IS=(U,A)、属性子集B⊆A和论域子集X⊆U，有

在决策系统DS=(U,A,d)中，{d}∩A=Ø，决策属性d将论域U划分为块，U/{d}={Y1,Y2,…,Yp}，其中Yi(i=1,2,…,p)是等价类.决策系统DS=(U,A,d)的正区域定义为

Pawlak约简及属性依赖度等概念定义如下：

定义1[1-3]在决策系统DS=(U,A,d)中，若B⊆A满足下列条件：

1)POSB(d)=POSA(d)；

2)对于任意S⊂B,有POSS(d)≠POSB(d).

则B⊆A是DS的约简.

2　可变正区域约简

现实中的数据常常带有一些异常点，这些异常点给分类造成一定的负面作用，现有的粗糙集模型，包括可变精度粗糙集，都不能解决这个问题.本文使用可变正区域的约简方式，在约简过程中不必严格保持正区域不变，试图解决这个问题.

定理1[23]设DS=(U,A,d)是一个决策系统,B1⊆B2⊆A,则POSB1(d)⊆POSB2(d)⊆POSA(d).

定义4在决策系统DS=(U,A,d)中，若B⊆A满足下列条件:

2)对于任意S⊂B,条件1)都不成立.

则称B⊆A为DS的ε可变正区域约简.其中,ε∈[0,1)是参数，其值根据需要指定.

当ε=0时，ε可变正区域约简就是Pawlak约简.所有ε可变正区域约简记为REDVP(DS).

定义5ε可变正区域约简的属性核定义为

命题1ε可变正区域约简是Pawlak约简的子集.

命题2ε可变正区域约简属性核是Pawlak约简属性核的子集.

证明根据命题1，ε可变正区域约简是Pawlak约简的子集，再根据ε可变正区域约简属性核和Pawlak约简属性核的定义，易知，ε可变正区域约简属性核是Pawlak约简属性核的子集.命题2证毕.

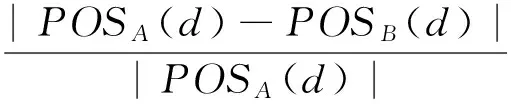
定理3在决策系统DS=(U,A,d)中,a∈A是DS的ε可变正区域约简的核属性当且仅当σ(A,a)≥ε.

证明必要性显然成立.

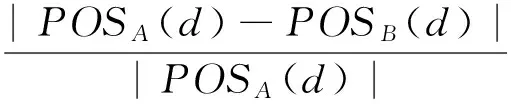
推论1在决策系统DS=(U,A,d)中,若ε>max{σ(A,a)|a∈A}，则ε可变正区域约简的属性核为空.

于是,ε可变正区域约简可以重新定义为:

定义6在决策系统DS=(U,A,d)中，若B⊆A满足下列条件：

2)对于任意S⊂B,条件1)都不成立.

则称B⊆A为DS的ε可变正区域约简.

3　ε可变正区域约简算法及示例

3.1ε可变正区域约简算法

与求取Pawlak约简算法类似，ε可变正区域约简算法的基本思想为:首先,根据选取的参数ε求取ε可变正区域约简的核属性；其次，根据除核属性以外的其他属性的重要度与参数ε求取约简中的剩余属性.算法的具体步骤如下：

算法:ε可变正区域约简算法

输入:决策系统DS=(U,A,d),参数ε.

输出:ε可变正区域约简.

算法步骤:

步骤1B=Ø,E=A.

步骤2对于任意的a∈A,若σ(A,a)≥ε,则B=B∪{a};//求取ε可变正区域约简的属性核.

步骤3E=A-B.

1)对于任意的a∈E,计算σ′(B,a),若σ′(B,a)=0,则E=E-{a};

2)选取最大的σ′(B,a),B=B∪{a},E=E-{a}.

步骤5输出ε可变正区域约简B.

ε可变正区域约简算法的时间复杂度等价于求解Pawlak约简的时间复杂度，其值取决于求等价类、求正区域方法的时间复杂度.所有求取Pawlak约简的算法都可以稍稍改造成求解ε可变正区域约简的算法.因为有很多求取Pawlak约简的算法,所以这里不估算ε可变正区域约简算法的时间复杂度.

注1由这个约简算法求取的ε可变正区域约简有可能是ε可变正区域约简的超集，即满足定义4的条件1)，但不一定满足条件2).若需要严格的ε可变正区域约简，则可删除部分冗余属性.但在一般情况下，这个算法得到的约简不含冗余属性，所以，本算法没有加上删除冗余属性的步骤.

3.2示例

如表1所示，DS=(U,A,d)是一个决策表，A={a,b,c}是条件属性集，d是决策属性.

显然,POSA(d)={y1,y2,y3,y4,y7},Pawlak约简为B=A={a,b,c}.对于条件属性c来说，除了c(y7)=1外，其余元素的值都为0,y7是异常点.如果用可变精度粗糙集处理,那么参数要大于0.5才能将属性c约简掉,而在可变精度粗糙集

表1　决策系统DS

中几乎不可能取大于0.5的参数；如果用可变正区域的方法进行约简，那么只需要取ε>0.2就能将属性c约简掉;如果将d(y7)的值换成2,而不是1,那么用可变精度粗糙集也同样难以处理,而用可变正区域的约简方法同样可以将属性c约简掉.

注2条件属性c是表1决策系统的核属性，但用可变正区域的约简方法可以将它约简掉.因为约简掉条件属性c对决策表DS的正区域影响较小.

4　结论与展望

与几乎所有的粗糙集约简模型不同，本文提出了一种可变正区域的粗糙集约简方法.该方法在约简时允许正区域发生一定程度的变化，不再严格保持约简准则不变或信息不变.理论分析和示例表明该方法能有效地将对正区域影响小的属性约简掉,对异常点检测、提高属性约简的分类泛化能力等具有一定的潜力和帮助.

进一步研究内容为,把可变正区域约简方法运用于异常点检测和提高约简的泛化能力，并和其他形式的约简和方法进行比较.

[1]PawlakZ.Roughsets[J].IntJInformComputSci,1982,11(5):341-356.

[2]PawlakZ.Roughsets:Theoreticalaspectofreasoningaboutdata[M].Dordrecht:KluwerAcademicPublishers,1991.

[3]王国胤.Rough集理论与知识获取[M].西安:西安交通大学出版社,2001.

[4]AnA,ShanN,ChanC,etal.Discoveringrulesforwaterdemandprediction:Anenhancedrough-setapproach[J].EngApplArtifInte,1996,9(6):645-653.

[5]KatzbergJD,ZiarkoW.Variableprecisionextensionofroughset[J].FoundInform,1996,27(2/3):155-168.

[9]ZhuW,WangFY.Reductionandaxiomizationofcoveringgeneralizedroughsets[J].InformSci,2003,152(1):217-230.

[10]ZhuW.Topologicalapproachestocoveringroughsets[J].InformSci,2007,177(6):1499-1508.

[11]ZhuW,WangFY.Onthreetypesofcovering-basedroughsets[J].IEEETransKnowlDataEng,2007,19(8):1131-1144.

[12]HuQ,ZhangL,ZhangD,etal.Measuringrelevancebetweendiscreteandcontinuousfeaturesbasedonneighborhoodmutualinformation[J].ExpertSystAppl,2011,38(9):10737-10750.

[13]LinTY.GranularcomputingonbinaryrelationsI:Dataminingandneighborhoodsystems,II:roughsetrepresentationsandbelieffunctions[C]//PolkowskiL,SkowronA.Roughsetsinknowledgediscovery.PhysicaVerlag:Springer,1998:107-140.

[14]LinTY.Neighborhoodsystems:aqualitativetheoryforfuzzyandroughsets[C]//WangP.Advancesinmachineintelligenceandsoftcomputing.Durham:DukeUniversity,1997:132-155.

[15]YaoYY.Informationgranulationandapproximationinadecision-theoreticalmodelofroughsets[C]//PolkowskiL,PalSK,SkowronA.Rough-neurocomputing:Techniquesforcomputingwithwords.Berlin:Springer,2003:491-516.

[16]YaoYY,WongSKM.Adecisiontheoreticframeworkforapproximatingconcepts[J].IntJManMachStud,1992,37(6):793-809.

[17]YaoYY,ZhaoY.Attributereductionindecision-theoreticroughsetmodels[J].InformSci,2008,178(17):3356-3373.

[18]邓大勇，陈林.并行约简与F-粗糙集[C]//王国胤，李德毅，姚一豫,等.云模型与粒计算.北京：科学出版社,2012:210-228.

[19]陈林.粗糙集中不同粒度层次下的并行约简及决策[D].金华:浙江师范大学,2013.

[20]苗夺谦，胡桂荣.知识约简的一种启发式算法[J].计算机研究与发展,1999,36(6):681-684.

[21]王国胤，于洪，杨大春.基于条件信息熵的决策表约简[J].计算机学报,2002,25(7):759-766.

[22]杨明.决策表中基于条件信息熵的近似约简[J].电子学报,2007,35(11):2156-2160.

[23]QianY,LiangJ,PedryczW,etal.Positiveapproximation:Anacceleratorforattributereductioninroughsettheory[J].ArtifInte,2010,174(9/10):597-618.

(责任编辑陶立方)

Attribute reduction of various positive region based on rough sets

DENG Dayong1,2,LI Ya′nan1,XUE Huanhuan1

(1.CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China; 2.XingzhiCollege,ZhejiangNormalUniversity,Jinhua321004,China)

Attribute reduction had been one of the hot topics in rough set theory. Almost all of principles for attribute reducts in various kinds of rough set models preserved specified criteria, which revealed shortcomings when they were employed in problems of generalization, if data contain outliers. In order to solve this problem, a reducing method called attribute reducts of various positive regions, was presented, in which the change of positive regions was allowed when attribute reduction was conducted. Theoretical analysis and an example showed that this method was valid.

rough sets; attribute reduction; various positive region; outlier; attribute significance

10.16218/j.issn.1001-5051.2016.03.010

收文日期：2015-12-07；2016-03-08

浙江省自然科学基金资助项目(LY15F020012)

邓大勇(1968-)，男，江西新干人，副教授.研究方向：数据挖掘；人工智能等.

TP18

A

1001-5051(2016)03-0294-04