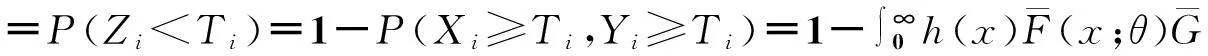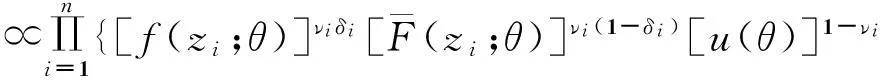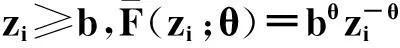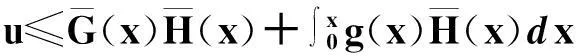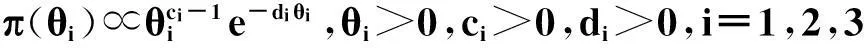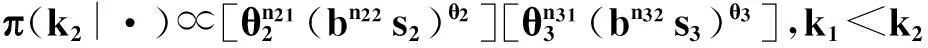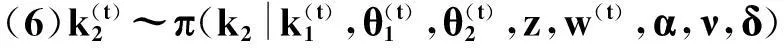左截断右删失数据下Pareto分布形状参数多变点的贝叶斯估计

何朝兵,杜保建,刘华文

(1. 安阳师范学院数学与统计学院,中国 安阳　455000; 2. 山东大学数学学院,中国 济南　250100)

左截断右删失数据下Pareto分布形状参数多变点的贝叶斯估计

何朝兵1*,杜保建1,刘华文2

(1. 安阳师范学院数学与统计学院,中国 安阳455000; 2. 山东大学数学学院,中国 济南250100)

摘要通过添加缺损的寿命变量数据得到了左截断右删失数据下Pareto分布相对简单的似然函数,给出了形状参数变点位置和其他参数的满条件分布.利用MCMC方法对参数的满条件分布进行了抽样,把Gibbs样本的均值作为参数的贝叶斯估计.随机模拟的结果表明各参数贝叶斯估计的精度都较高.

关键词似然函数;满条件分布;MCMC方法;Gibbs抽样;Metropolis-Hastings算法

Bayesian Estimation of Shape Parameter of Pareto Distribution with

Multiple Change Points for Left Truncated and Right Censored Data

HEChao-bing1*,DUBao-jian1,LIUHua-wen2

(1. School of Mathematics and Statistics, Anyang Normal University, Anyang 455000, China;

2. School of Mathematics, Shandong University, Ji’nan 250100, China)

AbstractBy filling in the missing data of the life variable, the relatively simple likelihood function of Pareto distribution for left truncated and right censored data is obtained. The full conditional distributions of change-point positions of shape parameter and other parameters are given. Each parameter is sampled from the full conditional distributions by MCMC method. The means of Gibbs samples are taken as Bayesian estimations of the parameters. The random simulation results show that Bayesian estimations of the parameters are fairly accurate.

Key wordslikelihood function; full conditional distribution; MCMC method; Gibbs sampling; Metropolis-Hastings algorithm

近年来变点问题成为统计学中比较热门的研究方向,它广泛应用于金融、经济和地震预测等领域.目前变点分析方法主要有极大似然法、贝叶斯法和非参数方法等.关于变点问题的研究可参看文献[1-4].而贝叶斯计算方法中的MCMC方法,使变点分析变得非常方便.Pareto分布在生存分析和可靠性理论等方面仍然具有很多应用价值.关于Pareto分布的研究可参看文献[5-7].当进行寿命试验时,经常会出现左截断右删失数据,对此模型的研究可参看文献[8-10].关于左截断或右删失数据下变点问题的研究有一些成果,可参看文献[11-13],但对数据既左截断又右删失情形下变点问题的研究还不多见.本文主要利用MCMC方法研究左截断右删失数据下Pareto分布形状参数多变点的贝叶斯估计.

1左截断右删失数据试验模型

设(X,Y,T)是一连续型随机变量,寿命变量X的分布函数为F(x;θ)=P(X≤x),密度函数为f(x;θ),这里θ是未知参数;Y是一右删失随机变量,分布函数为G(y),密度函数为g(y);T是一左截断随机变量,分布函数为H(t),密度函数为h(t),且Y,T的分布与参数θ无关.假定X,Y,T是相互独立非负随机变量.对于n个受试样品(产品寿命),左截断右删失数据的试验模型是仅在Zi≥Ti时得到观察数据(Zi,Ti,δi),而在Zi

Zi=Xi∧Yi=min(Xi,Yi),δi=I(Xi≤Yi),i=1,2,…,n.

下面求样本的似然函数.

为了研究方便,引入示性变量νi=I(min(Xi,Yi)≥Ti),i=1,2,…,n.则基于观察数据{(zi,ti,δi):νi=1,1≤i≤n}的似然函数为

2左截断右删失数据下Pareto分布的似然函数

若X的密度函数为f(x)=θbθx-(θ+1),x≥b>0,θ>0,则称X服从尺度参数为b,形状参数为θ的Pareto分布,记为X~Pa(b,θ),易知X的分布函数为F(x)=1-bθx-θ,x≥b.

左截断右删失数据试验模型中,假设产品寿命X~Pa(b,θ),且b已知.

令δ,z,ν分别表示由δi,zi,νi组成的向量,则似然函数为

(1)

由(1)式易知,左截断右删失数据下Pareto分布的似然函数比较复杂.

下面添加部分缺损的Xi的值,以获得较简单的似然函数.具体如下:

当νi=0时,添加数据Z1i=Xi=z1i.

在νi=0,即min(Xi,Yi)

ψ(x;θ)=[u(θ)]-1f(x;θ)P({Y>x,T>x}∪{Y≤x,T>Y})=

可以利用筛选法随机产生Z1i的值z1i.z1i抽样的具体步骤如下：

(1)由均匀分布U(0,1)抽取u,由f(x;θ)抽取x;

令αi=I(zi≥b),令α,w分别表示由αi,z1i组成的向量,则添加数据后的似然函数为

(2)

3左截断右删失数据下Pareto分布形状参数多变点的贝叶斯估计

Pareto分布形状参数多变点模型如下:

(3)

其中θ1,θ2,θ3两两不相等,1≤k1

下面利用贝叶斯方法对对变点位置k1,k2及参数θ1,θ2,θ3进行估计.

令D1={1,2,…,k1},D2={k1+1,…,k2},D3={k2+1,…,n}.

记β=(k1,k2,θ1,θ2,θ3),由(2)式和(3)式可得此变点问题的似然函数为

其中nm1=n1(Dm),nm2=n2(Dm),sm=s(Dm),m=1,2,3.

下面确定各参数的先验分布.

(2) 取θi的先验分布为伽玛分布Ga(ci,di),ci,di已知,即

假设(k1,k2),θ1,θ2,θ3相互独立,则

L(β|z,w,α,ν,δ)∝π(k1,k2)π(θ1)π(θ2)π(θ3)L(z,w,α,ν,δ|β)

其中z-1i={z1j:j≠i}.

记π(θ1|·)=π(θ1|k1,k2,θ2,θ3,z,w,α,ν,δ).

下面求各参数的满条件分布.

利用筛选法随机抽取z1i;采用θ1,θ2,θ3直接对Gibbs抽样;利用Metropolis-Hastings算法对k1,k2进行抽样.下面写出MCMC方法的具体步骤.

4随机模拟

下面进行随机模拟试验.取受试样品的个数n=200.

假设Pareto分布的尺度参数8是已知的,取θ1,θ2,θ3的先验分布分别为Ga(3.5,6),Ga(20,1.6),Ga(17,2.6);右删失变量Yi~Pa(10,2),左截断变量Ti~Pa(6,10).则(k1,k2,θ1,θ2,θ3)的真实值为(80,150,0.7,13,6).

使用R软件进行MCMC模拟,主要对参数k1,k2进行估计分析.在模拟过程中,先进行10 000次Gibbs预迭代,以确保抽样的收敛性,然后丢弃最初的预迭代,再进行10 000次Gibbs迭代.迭代从第10 001次开始至第20 000次的R程序的运行结果见表1.

表1　参数k1, k2,θ1,θ2,θ3的贝叶斯估计

变点位置参数的Gibbs抽样迭代过程见图1和图2.

图1　参数k1的Gibbs抽样迭代过程　　　　　　　　　　　　图2　参数k2的Gibbs抽样迭代过程Fig.1　Gibbs sampling iterations of k1 　　　　　　　　　　　　　　　　Fig.2　Gibbs sampling iterations of k2

在模型的分析过程中,MCMC的收敛性诊断很重要,模拟时可以对参数进行多层链式迭代分析,即输入多组初始值,形成多层迭代链,当抽样收敛时,迭代图形重合.在模拟过程中,输入两组初始值分别进行10 000次迭代,变点位置参数的多层迭代链轨迹见图3和图4.

图3　k1的多层迭代链轨迹　　　　　　　　　　　　　　　图4　k2的多层迭代链轨迹Fig.3　Multiple iterative chains trace of k1 　　　　　　　　　　　　　Fig.4　Multiple iterative chains trace of k2

最后,进行模拟结果分析.首先,由表1可以看出位置参数的贝叶斯估计与真值的相对误差不超过4%,其他参数估计的相对误差不超过9%,整体上估计的精度较高,效果较好；其次,要判断所产生的马尔科夫链是否收敛,由图3和图4可以发现,变点位置参数的两条迭代链都趋于重合,收敛性较好.综上分析,可以看出通过MCMC方法模拟所产生的效果较好.

参考文献：

[1]PAGE E S. Continuous inspection schemes[J]. Biometrika, 1954,41(1):100-115.

[2]CSÖRGÖ M, HORVTH L. Limit theorems in change-point analysis[M]. New York: Wiley, 1997.

[3]CHERNOFF H, ZACKS S. Estimating the current mean of a normal distribution which is subjected to changes in time[J]. Ann Math Stat, 1964,35(3):999-1018.

[4]FEARNHEAD P. Exact and efficient Bayesian inference for multiple changepoint problems[J]. Stat Comput, 2006,16(2):203-213.

[5]ARNOLD B C. Pareto distribution[M]. New York: John Wiley & Sons, Inc, 1985.

[6]CASTILLO J, DAOUDI J. Estimation of the generalized Pareto distribution[J]. Stat Probab Lett, 2009,79(5):684-688.

[7]KAMAL M, ZARRIN S, ISLAM A U. Accelerated life testing design using geometric process for Pareto distribution[J]. Int J Adv Stat Probab, 2013,1(2):25-31.

[8]BALAKRISHNAN N, MITRA D. Likelihood inference for lognormal data with left truncation and right censoring with an illustration[J]. J Stat Plann Inference, 2011,141(11):3536-3553.

[9]COSSLETT S R. Efficient semiparametric estimation of censored and truncated regressions via a smoothed self-consistency equation[J]. Econometrica, 2004,72(4):1277-1293.

[10]GROSS S T, LAI T L. Nonparametric estimation and regression analysis with left-truncated and right-censored data[J]. J Am Stat Assoc, 1996,91(435):1166-1180.

[11]ANTONIADIS A, GRÉGOIRE G. Nonparametric estimation in change point hazard rate models for censored data: A counting process approach[J]. J Nonparametr Stat, 1993,3(2):135-154.

[12]ANTONIADIS A, GIJBELS I, MACGIBBON B. Nonparametric estimation for the location of a change-point in an otherwise smooth hazard function under random censoring[J]. Scand J Stat, 2000,27(3):501-519.

[13]GIJBELS I, GÜRLER Ü. Estimation of a change point in a hazard function based on censored data[J]. Lifetime Data Anal, 2003,9(4):395-411.

(编辑胡文杰)

*通讯作者,E-mail：chaobing5@163.com

基金项目：国家自然科学基金资助项目(61174099); 河南省教育厅科学技术研究重点项目(14B110011)

收稿日期：2014-02-28

中图分类号O213.2; O212.8

文献标识码A

文章编号1000-2537(2015)03-0080-05

DOI:10.7612/j.issn.1000-2537.2015.03.015