随机荷载作用下刚性路面动态响应研究
随机荷载作用下刚性路面动态响应研究
张献民,胡鹏
(中国民航大学机场学院,天津300300)
摘要:为了研究车辆随机荷载作用下刚性路面的动态响应,基于ANSYS软件,应用1/4车辆模型,得出其在路面不平度激励下的随机荷载,简化了荷载的求解,建立了路面三维有限元模型,讨论了在随机荷载作用下结构层参数对路面动位移幅值及面层层底拉应力幅值的影响规律。结果表明,面层厚度和土基模量对路面动位移幅值影响最大,当面层厚度超过30cm、土基模量超过60MPa时,继续增大以上结构层参数路面动位移幅值不再有明显减少;当土基模量小于60MPa继续减少时,要实现路面动位移幅值的不变,需要增加的面层厚度幅度逐渐变大;面层模量及厚度对面层层底拉应力幅值影响最大。
关键词:道路工程;刚性路面;三维有限元;结构层参数;随机荷载;动位移幅值;层底拉应力幅值
中图分类号:U416.222
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.19.020
Abstract:In order to study the dynamic response of a rigid pavement under vehcle random loads, a vehicle random load excited by pavement surface roughness was obtained with application of a 1/4 vehicle model based on ANSYS, the load-solving was simplified. Then, a 3D finite element model of the pavement was established to discuss the influences of structural parameters on the maximum dynamic displacement and the maximum bottom tensile stress of the surface layer under the random load. The calculated results indicated that subgrade modulus and surface layer thickness have significant effects on the maximum dynamic displacement; when the surface layer thickness is more than 30 cm, the subgrade modulus is more than 60 MPa, continuously increasing these parameters can not cause the maximum dynamic displacement to decrease obviously; when the subgrade modulus is less than 60 MPa, it needs a gradual increase in surface layer thickness to keep the maximum dynamic displacement from changing while the subgrade modulus decreases; the surface layer modulus and thickness have the largest influence on the maximum bottom tensile stress of the surface layer.
基金项目:国家自然科学基金项目(U1334201,51278434);铁道部重大科研课题(2009G004-D) 华南理工大学风工程广东省普通高校重点实验室开放研究基金课题资助(1302)
收稿日期:2014-04-23修改稿收到日期:2014-09-25 2014-08-21修改稿收到日期:2014-10-11
Dynamic response of a rigid pavement under random loads
ZHANGXian-min,HUPeng(Airport College ,Civil Aviation University of China, Tianjin 300300, China)
Key words:road engineering; rigid pavement; 3D finite element; structural parameters; random load; maximum dynamic displacement; maximum bottom tensile stress
在目前的路面设计中,车辆荷载被当作静荷载处理[1],但汽车在行驶过程中,由于路面不平度的激励,产生的是随机动荷载。动载与静载对路面的作用有着本质的区别,所以简单按照静载处理的设计理论显然与实际不符。各国学者在路面动态响应的研究中取得了丰硕的成果,邓学钧[2]将车辆与地面视为综合体系,开创了车辆地面动力学理论的新体系。侯芸等[3]运用Newmark积分法逐步求解运动方程,分析了动载作用下多层弹性体系的响应。张文斌等[4]研究了移动常载荷与谐波载荷作用下刚性路面的动态应变响应。周玉明等[5]将车辆简化为1/4车辆模型,路面视为地基板,采用直接积分法求解。刘小云等[6]运用多重广义积分运算求解了路面响应的主要数字特征。卢正等[7]提出了车辆-不平整路面-路基结构耦合动力学分析模型,采用Fourier变换方法推导出了车辆附加动荷载和路面动力响应的解析表达式。然而,以往研究中的汽车荷载或被简化为稳态简谐振动,过于简单,或涉及到复杂微分方程的求解,使得实际应用受到限制。另外,在结构层参数对刚性路面受力及变形影响规律中的研究还不够深入。
基于以上问题,本文应用ANSYS软件,求解 1/4车辆模型在不平度激励下的随机荷载,简化了荷载的求解过程,并分析了不同结构层参数下刚性路面动态响应规律,相应结果能够为路面结构的优化设计提供理论参考。
1不同等级路面的生成
大量的试验表明,路面平整度是具有零均值、各态历经平稳的高斯随机过程,而谐波叠加法可以模拟此过程,因此本文运用上述方法将路面平整度表示成大量的随机相位的正弦或余弦波的叠加[8]。
目前国内外标准均建议路面功率谱密度Gq(n)按下式拟合:
(1)
式中:n为空间频率(m-1);n0为参考空间频率,n0=0.1m-1;Gq(n0)为参考空间频率n0的功率谱密度(m3);ω为频率指数,一般等于2;nl,nu为有效频率的上下限,若汽车振动的主要固有频率范围为(f1,f2),则nl=f1/v,nu=f2/v,v为行车速度。
采样的距离间隔△x应该满足:
(2)
由式(1)可得到路面平整度值的方差为:
(3)
将区间[nl,nu]划分为n个区间,用每个小区间的中心空间频率nmid_i处的功率谱密度值Gq(nmid_i)来代替Gq(n)。式(2)就可以近似写为
(4)

(5)
式中:x为路面水平位移;θi为[0,2π]上的随机数,满足正态分布。
根据以上步骤,生成的A、B级随机路面见图1。

图1 A,B级路面不平整度 Fig.1 Pavement surface roughness of grade A and B
2随机荷载的求解
汽车研究部门的实验表明,1/4车辆模型在车辆垂直振动方面的研究很成功,无需使用更复杂的模型,因此本文采用公路工程中常用的二自由度1/4车辆模型见图2。
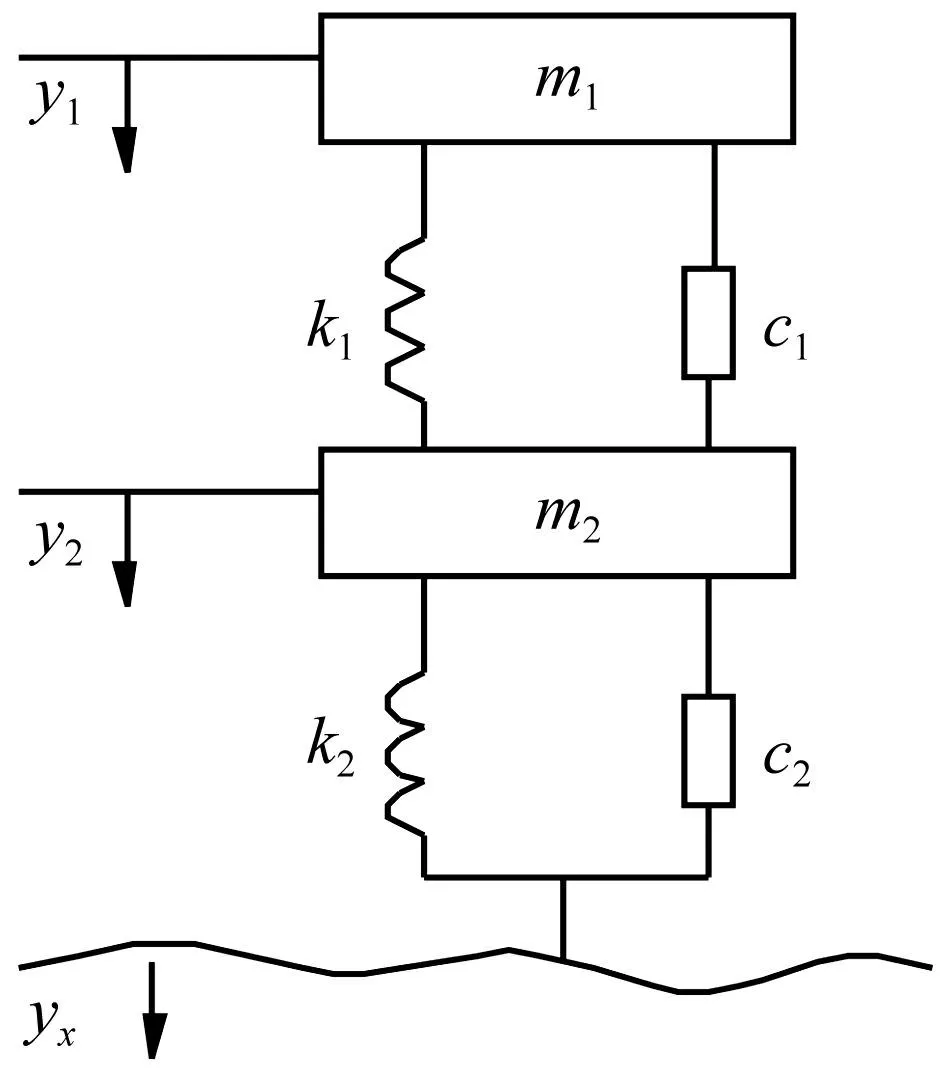
图2 1/4车辆模型 Fig.2 Quarter vehicle model
其振动微分方程如下:
(6)
式中:m1,m2分别为悬挂和非悬挂质量;k1,k2为悬挂和非悬挂刚度;c1,c2为悬挂和非悬挂阻尼。
则车辆对地面荷载为:
(7)
运用ANSYS软件,通过质量单元和弹簧单元建立1/4车辆模型,以路面不平度为约束,以加载的时间控制速度,采用Full法求解动荷载,并定义一维数组将求得的随机荷载备份,以便后续加载。图3为10t货车以15m/s速度通过A、B级路面的动荷载。车辆参数见表1[8]。

表1 10t货车参数

图3 A,B级路面随机荷载 Fig.3 Random load of grade A and B
3有限元模型的建立
本文将路面结构简化为面层、基层、垫层和地基构成的弹性层状体系,通过试算并结合文献[9]确定有限元模型大小为15m×6m×6m,面层为6块5m×3m水泥混凝土板拼接而成,x轴为行车方向,y轴沿深度方向,z轴为路面宽度方向。边界条件的确定参考文献[10]:x=0m及x=15m处只约束x方向;y=0m处固定约束;z=0m及z=6m处只约束z方向。模型见图4。
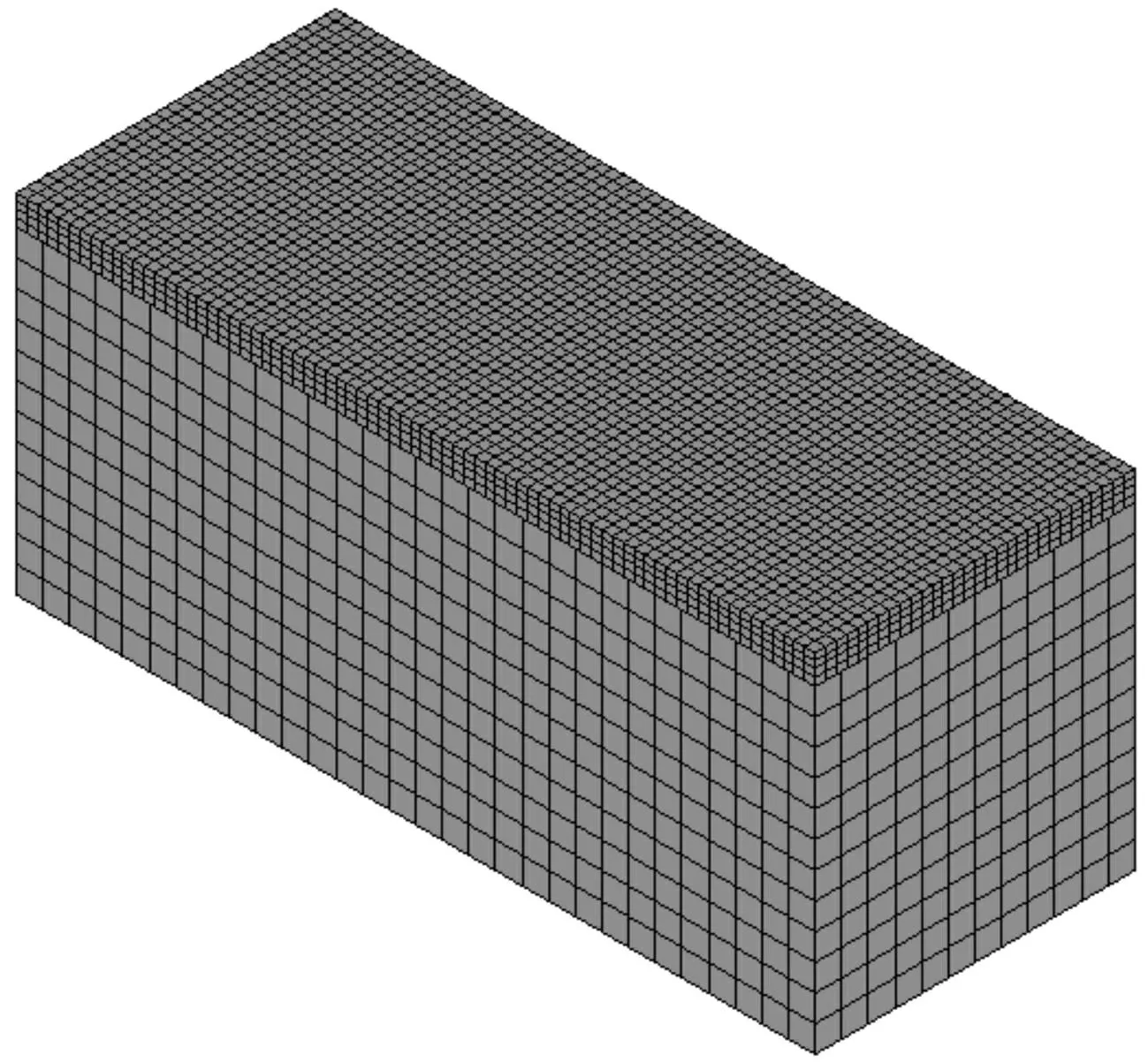
图4 道路有限元模型 Fig.4 Finite element model of pavement
参考文献在进行路面动态响应分析时,轮胎的接地面积为0.3 m×0.226 m`([11]),加载方式[12],选取路面中心线为行车路线,确定轮载在在有限元模型上的作用位置,读入得出的随机荷载,在起点选择一组单元,施加持续时间为t的轮载;选择第二组单元,施加新的轮载,持续时间不变。这样采用阶跃的方式加载直到终点,以每个单元加载时间实现不同车速,加载过程见图5。

图5 车辆动荷载作用示意图 Fig.5 Schematic diagram of vehicle dynamic load
4计算结果分析
由于在混凝土路面设计方法中,都是以面层的弯拉应力作为极限状态和设计控制指标,所以,本文主要研究面层顶部的动位移和面层层底的拉应力。图6为10t货车在B级路面以15m/s速度行驶的情况下0.544s时路面垂直动位移云图,由文献[13]知路面板的临界荷位一般为纵缝边缘中部位置,故选择路面中点为观测点,图7为路面中点面层顶部动位移时程曲线及面层层底拉应力时程曲线,各结构层初始工况见表2。
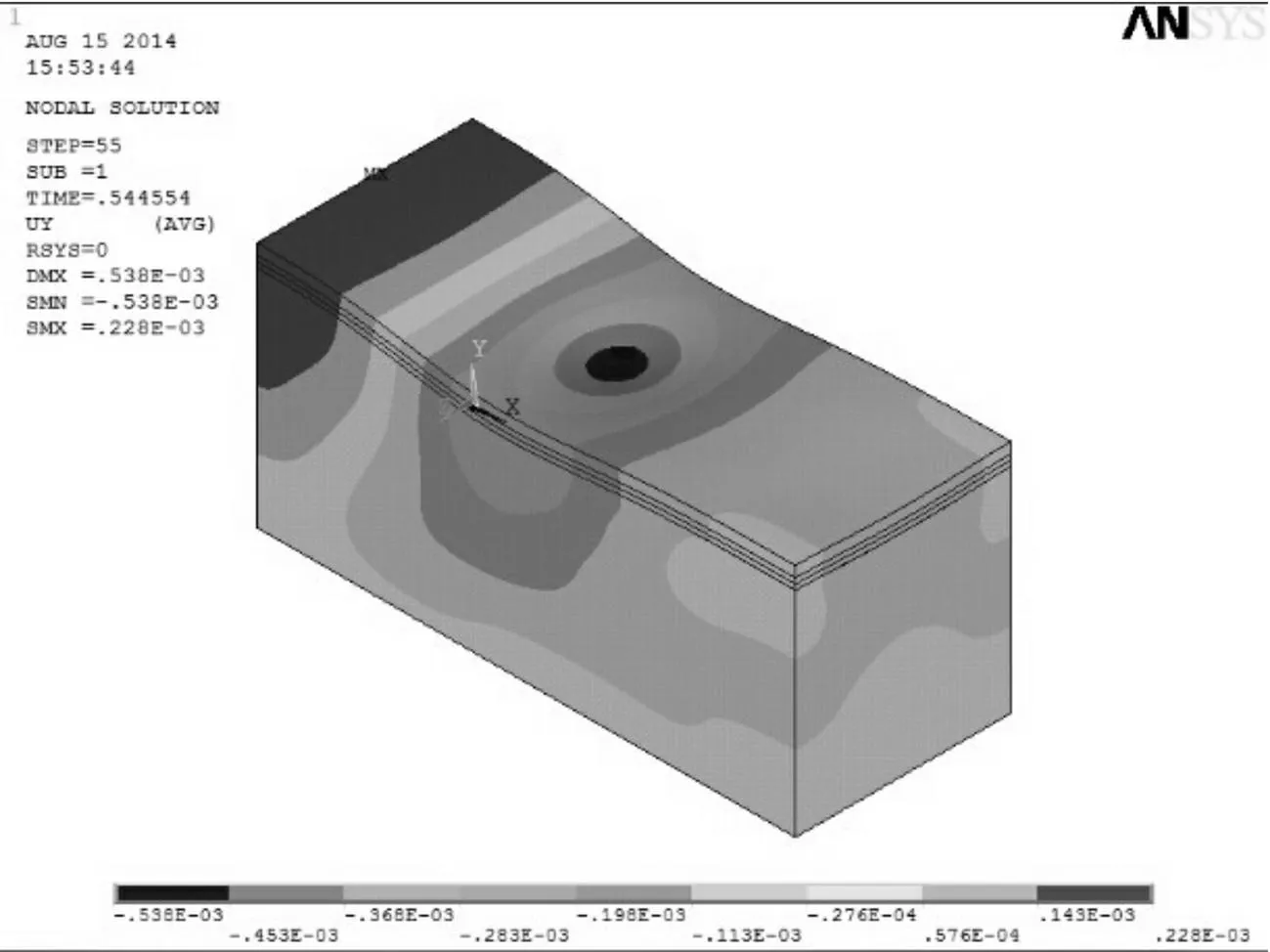
图6 路面动位移 Fig.6 Dynamic displacement of pavement

图7 时间历程响应 Fig.7 Response of time history
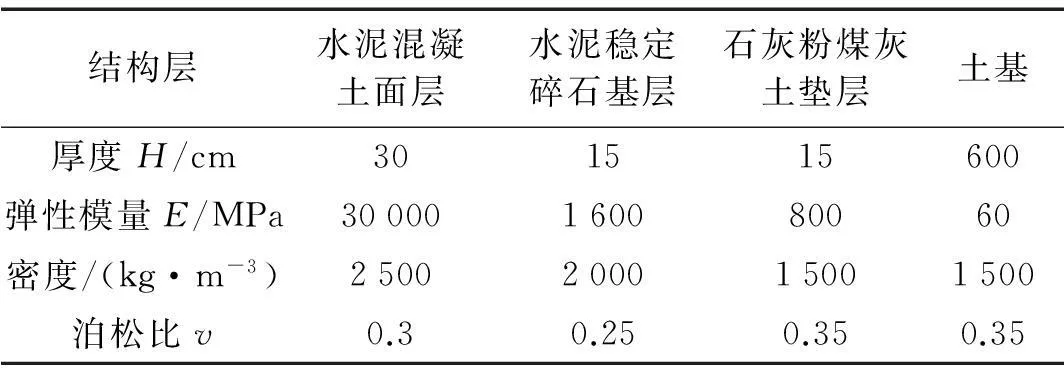
结构层水泥混凝土面层水泥稳定碎石基层石灰粉煤灰土垫层土基厚度H/cm301515600弹性模量E/MPa30000160080060密度/(kg·m-3)2500200015001500泊松比v0.30.250.350.35
为探讨结构层参数对上述指标的影响,依次改变面层、基层和土基参数的取值,但加载条件不变,分析不同工况下观测点动位移幅值和层底拉应力幅值的变化规律。
4.1 面层模量
其他结构层参数不变,面层模量从10GPa变化到50GPa,计算结果见图8。由图可知,随面层模量的变化层底拉应力幅值接近线性增长,通过线性拟合,相关性系数为0.9908,且变化幅度较大,50GPa时的层底拉应力幅值为10GPa时的2.35倍,这样的变化规律究其原因是因为σ=Eε,在相同受力条件下弹性模量增加会使应变减小,但二者的乘积仍呈现增大趋势,这与文献[14]结论相似;而动位移幅值的变化趋势却不尽相同,当面层模量从10GPa增长到30GPa时,动位移幅值减少了24.8%,而从30GPa增长到50GPa时仅减少了4.9%,因此,当面层模量超过30GPa时,继续增加面层模量,动位移幅值不会明显减少,但总体来说10GPa到50GPa面层模量的增加只引起0.21mm动位移幅值的减少,所以面层模量对动位移幅值的影响较小。

图8 面层模量对层底拉应力及动位移的影响 Fig.8 Effect of surface layer modulus on bottom tensile stress and dynamic displacement
4.2 面层厚度
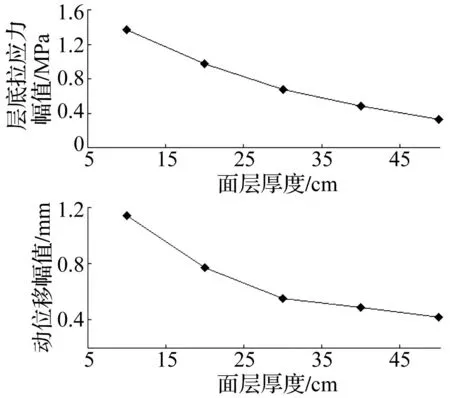
图9 面层厚度对层底拉应力及动位移的影响 Fig.9 Effect of surface layer thickness on bottom tensile stress and dynamic displacement
其他结构层参数不变,面层厚度从10cm变化到50cm,计算结果见图9。由图可知,随面层厚度的增加,层底拉应力幅值显著减小且变化率逐渐降低,即面层厚度从10cm增加到20cm,层底拉应力幅值减少0.4MPa,但从40cm增加到50cm,仅减少了0.12MPa,由此可见过薄的板厚对路面受力不利;当面层厚度从10cm增加到20cm时,动位移幅值减幅较大为38.6%,从20cm增加到30cm时减幅变小为21.4%,但超过30cm后动位移幅值变化幅度不大,可认为板厚超过30cm时,动位移幅值不再有明显变化。
4.3 基层模量和基层厚度
其他结构层参数不变,基层模量从1000MPa变化到3000MPa,计算结果见图10。由图可知,基层模量从1000MPa增加到3000MPa,层底拉应力幅值仅降低0.11MPa,动位移幅值也只减少0.05mm。
基层厚度从15cm增加到35cm,计算结果见图11。由图可知,基层厚度增加对层底拉应力幅值及动位移幅值的削弱作用很小,20cm基层厚度的增加,只引起了0.19MPa层底拉应力幅值和0.11mm动位移幅值的减少。

图10 基层模量对层底拉应力及动位移的影响 Fig.9 Effect of base course modulus on bottom tensile stress and dynamic displacement

图11 基层厚度对层底拉应力及动位移的影响 Fig.11 Effect of base course thickness on bottom tensile stress and dynamic displacement
通过计算可知基层模量及基层厚度对层底拉应力幅值及动位移幅值的影响不大,通过增加基层模量或基层厚度来提高承载力和抗变形能力的效果不明显。
4.4 土基模量
其他结构层参数不变,土基模量从20MPa变化到100MPa,计算结果见图12。由图可知土基模量的增大会减少层底拉应力幅值,但影响并不显著;土基模量从20MPa增加到60MPa,动位移幅值减少了56.7%,超过60MPa时,动位移幅值不再明显减少,可见过高的土基模量对减少动位移的作用不大。
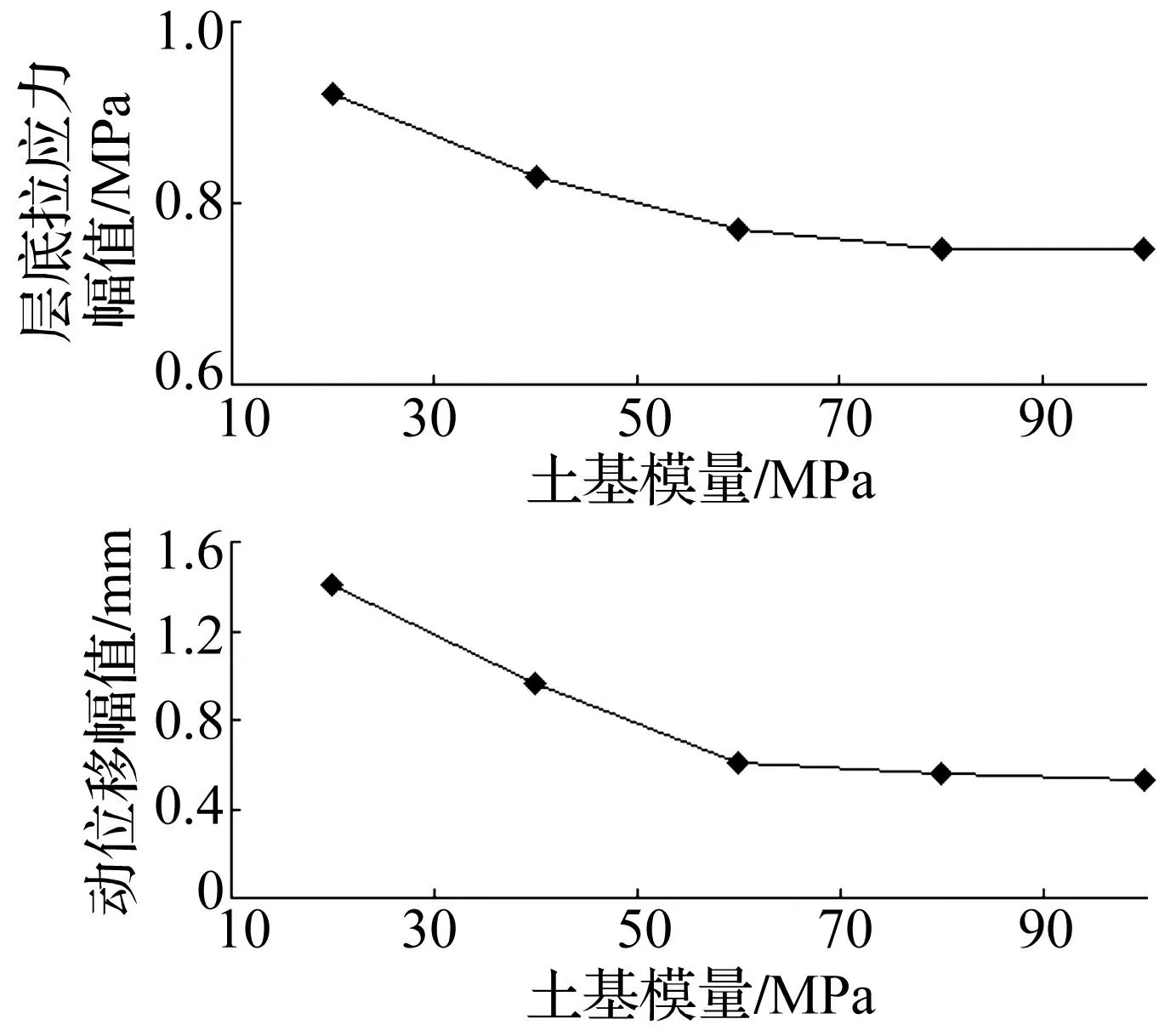
图12 土基模量对层底拉应力及动位移的影响 Fig.12 Effect of subgrade modulus on bottom tensile stress and dynamic displacement
4.5 动位移幅值不变时结构层参数组合分析
通过上述分析可知,面层厚度及土基模量对路面动位幅值移影响最大。在实际工程中,受施工条件的影响,有时需要调整结构层参数组合来达到相同的抗变形能力。为此本节在参考点动位移幅值不变的前提下,重点探讨较为合适的面层厚度和土基模量组合。
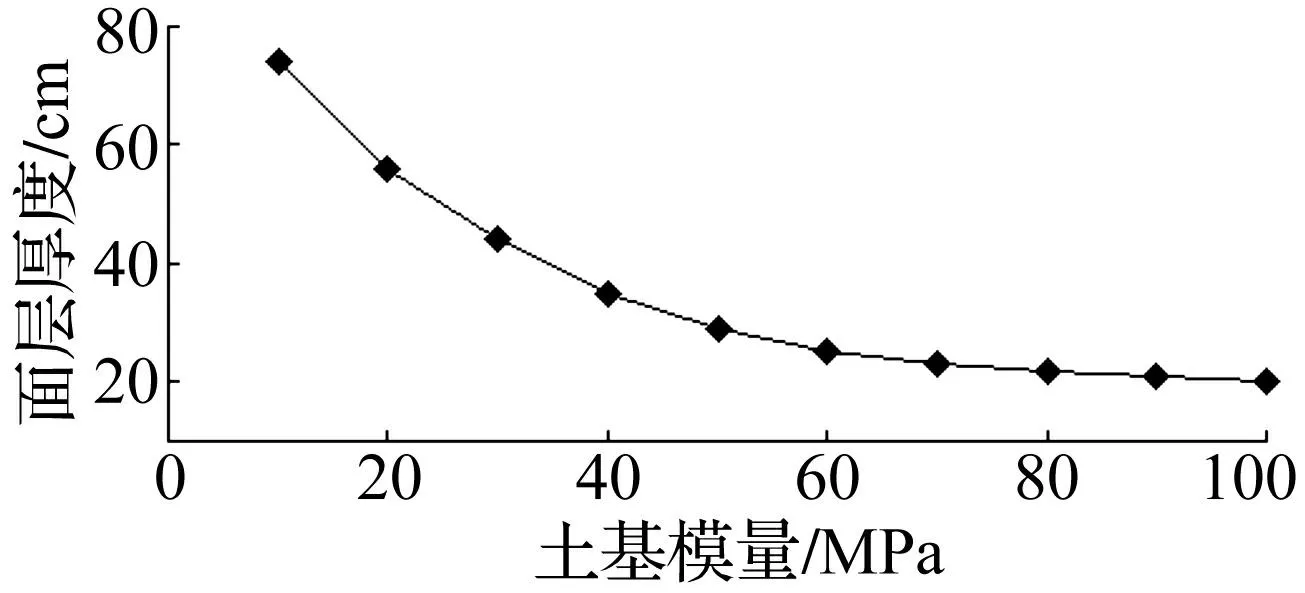
图13 面层厚度随土基模量的变化曲线 Fig.13 Surface layer thickness vs. subgrade modulus
选定面层厚度30cm、土基模量60MPa时的动位移幅值0.61mm为参考值。通过计算得到了土基模量10MPa到100MPa时所需的面层厚度。计算结果见图13。当土基模量从100MPa减少到60MPa时,面层厚度增加了25%,但当土基模量从60MPa减少到10MPa时,面层厚度增加了196%,且当土基模量小于60MPa继续减小时,要实现动位移幅值相等,需要增加的面层厚度幅度逐渐增加。究其原因,可以从5.2及5.4结论看出,当土基模量大于60MPa时,动位移幅值不再显著增加,所以面层厚度小幅度的增加就能满足动位移幅值的相等,但土基模量小于60MPa时,动位移幅值会明显增大,只有较大增加面层厚度才能实现动位移幅值的相等。
5结论
本文基于ANSYS软件,求得了1/4车辆模型在不平整路面激励下的随机荷载,深入探讨了不同结构层参数对混凝土路面动态响应的影响规律,该计算结果可为刚性路面的优化设计提供参考,结论如下:
(1)面层模量和面层厚度对层底拉应力幅值影响显著,而基层模量、基层厚度及土基模量的影响却很微弱。面层模量的增加不利于板底的受力,却一定程度减少了路面的动位移幅值:同理面层厚度的增加虽然减少了板底的受力,也会增加工程造价,所以应根据实际情况选择合理的面层模量和厚度。
(2)面层厚度及土基模量对路面动位移幅值影响最大,面层模量的影响相对较小,基层模量和基层厚度的影响很微弱。通过计算发现,当面层模量超过30GPa时,继续增加面层模量路面动位移幅值不再明显减少,而且当面层厚度超过30cm、土基模量超过60MPa时有同样的规律。所以盲目的增大结构层参数不一定能提高路面抗变形能力。
(3)探讨了对路面动位移幅值影响最大的面层厚度及土基模量的组合关系,通过计算发现,在其他结构层参数不变的条件下,当土基模量小于60MPa继续减小时,要实现动位移幅值的相等,需要增加的面层厚度幅度逐渐增大。因此在实际施工工程中,应优先确保土基的压实强度,以使具有相同结构参数的面层结构具有更好的抗变形能力。
[1]JTGD40-2002.公路水泥混凝土路面设计规范[S].北京:人民交通出版社,2002.
[2]邓学钧. 车辆-地面结构系统动力学研究[J]. 东南大学学报,2002,32(3):474-479.
DENG Xue-jun. Dynamics of vehicle-ground pavement structure system study [J]. Journal of Southeast University, 2002,32(3):474-479.
[3]侯芸,郭忠印,田波,等. 动荷作用下沥青路面结构的变形响应分析[J]. 中国公路学报,2002, 15 (3):6-10.
HOU Yun, GUO Zhong-yin, TIAN Bo, et al. Dynamicdeflection response of layered pavement structure subj-ectedto dynamic load [J]. China Journal of Highway and Transport,2002,15 (3):6-10.
[4]张文斌,王祁,马松林,等. 刚性路面动态应变响应的变换域分析[J]. 交通运输工程学报,2007,7(4):48-53.
ZHANG Wen-bin,WANG Qi, MA Song-lin, et all. Transform domain analysis of rigid pavement dynamic strain response[J]. Journal of Traffic and Transportation Engin-eerxing,2007, 7(4): 48-53.
[5]周玉民,谈至明,刘伯莹. 1/4车-路耦合动力学模型研究[J]. 同济大学学报:自然科学版,2012,40(3):408-413.
ZHOU Yu-min,TAN Zhi-ming,LIU Bo-ying.Study on the quartered vehicle-road coupling dynamics models[J].Jour-Nal of Tongji University:Nature Science,2012,40(3):408-413.
[6]Liu Xiao-yun,Shi Chun-juan,Chen Shui-jing.A theory research of asphalt pavement dynamic response under ve-hicle random stimulation[J].Applied Mechanics and Mate-rials,2012,105(1):13-19
[7]卢正,姚海林,胡智. 基于车辆-道路结构耦合振动的不平整路面动力响应分析[J]. 岩土工程学报,2013,35(1):232-238.
LU Zheng,YAO Hai-lin,HU Zhi. Dynamic response anal-ysisof rough pavement under vehicle-road systemcou-pledvibration[J]. Chinese Journal of Geotechnical Engineering,2013,35(1): 232-238.
[8]苏世毅. 考虑路面平整度因素的车辆-道路耦合系统动力特性分析[D].重庆:重庆交通大学,2008.
[9]李皓玉. 车辆与路面相互作用下路面结构动力学研究[D].北京:北京交通大学,2011.
[10]郑元勋,蔡迎春,张亚敏. 沥青混凝土路面动力特性数值模拟研究[J]. 公路,2012,3(3):84-89.
ZHENG Yuan-xun,CAI Yin-chun,ZHANG Ya-min. The dyna-mic characteristics of asphalt concrete pavement nume-rical simulation research[J]. Highway,2012,3(3): 84-89.
[11]李皓玉,杨绍普,李韶华. 车、路的相互作用下沥青路面动力学特性分析[J]. 振动与冲击,2009,28(4):87-89.
LI Hao-yu,YANG Shao-pu,LI Shao-hua. Dynamical analysis of an asphalt pavement due to vehicle-road interaction[J].Journal of Vibration and Shock,2009,28(4):87-89.
[12]Wu C P,Shen P A,Dynamic analysis of concrete pavements subjected to moving loads[J].Journal of Transportation Engineering,1996,122(5):367-373.
[13]于宝明,姚祖康. 混凝土路面临界荷位分析[J]. 中国公路学报,1989,2(1):1-10.
YU Bao-ming,YAO Zu-kang.A study of critical loading posi-tion for concrete pavements[J]. China Journal of Highway and Transport,1989,2(1):1-10.
[14]付欣. 动荷载作用下水泥混凝土路面的有限元分析[J]. 华东公路,2010,6:58-62.
FU Xin. Thefinite element analysis of cement concrete pavement under dynamic load [J].East Chinh High-way,2010,6:58-62.

第一作者李永乐男,博士,教授,博士生导师,1972年生

第一作者韩志惠女,博士,1985年生
通信作者顾明男,博士,教授,博士生导师,1957年生

