螺杆真空泵自平衡螺杆转子优化设计

螺杆真空泵自平衡螺杆转子优化设计

巫修海1,2，陈文华1，张宝夫2

(1.浙江理工大学浙江省机电产品可靠性技术研究重点实验室，杭州310018;2.台州职业技术学院机电工程学院，浙江台州318000)

摘要：为了开发能适应恶劣工况、高效节能和安全运行的螺杆真空泵，设计了一种自平衡的内部压缩螺杆转子模型。使用借助Hermite插值理论导出圆柱变螺距螺旋线的参数方程，构建了变螺距设计参数、尾部压缩级数与螺旋角度的变量关系式，建立了自平衡螺杆转子优化设计模型。通过计算，优化转子质量轴向分布，无需在螺杆转子两端和齿顶减重而达到良好的自身动平衡，动平衡试验证明了设计模型的可靠性，为螺杆真空泵的动平衡研究提供了参考依据。

关键词：螺杆真空泵;静平衡;动平衡;螺杆转子;变螺距

中图分类号:O347.6

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.023

Abstract:In order to develop screw vacuum pumps working efficiently, running safely and adapting to bad working conditions, a screw rotor with automatic dynamic balancing and changes in volume was designed. The cylinder variable pitch helicaline parameter equation was derived using Hermit’s interpolation theory. The relationships among variable pitch design parameters, tail compression stages and spiral angle were established. Then, the optimal design model for a screw rotor with automitic dynamic balance was built. Through calculation, the axial distribution of the rotor mass was optimized, the dynamic balance reached without the weight subtraction at both ends and tooth tip of the rotor. The reliability of the design model was verified with the dynamic balance tests. The results provided a reference for studying dynamic balance of screw vacuum pumps.

基金项目：国家自然科学基金(51309239,41206042);青岛市科技计划项目(13-1-4-216-jch) 国家自然科学基金(51303081);江苏省自然科学基金(BK20130761);江苏省普通高校学术学位研究生科研创新计划(KYLX_0398)

收稿日期：2015-02-08修改稿收到日期：2015-04-07 2015-01-16修改稿收到日期：2015-04-15

Optimization design of screw rotor with automatic dynamic balance of a screw vacuum pump

WUXiu-hai1,2,CHENWen-hua1,ZHANGBao-fu2(1. Zhejiang Provincie’s Key Laboratory of Reliability Technology for Mechanical and Electrical Products, Zhejiang Sci-Tech University, Hangzhou 310018, China;2. Mechanical & Electrical Engineering College, Taizhou Vocational and Technical College, Taizhou 318000, China)

Key words:screw vacuum pump; static balance; dynamic balance; screw rotor; variable pitch

螺杆真空泵由螺杆空压机演变而来，用来抽取气体，产生真空泵环境，由于其是一种理想的真空获得设备，结构简单，维护方便，在使用过程中对环境友好，不会产生污染，已经成为微电子、半导体、制药、精密加工等行业首选真空获得设备[1]，特别是各种内压缩的干式螺杆真空泵由于高效节能和低噪声，业已成为目前开发的热点。螺杆式空压机的螺杆型线都是多头型线，其自身具有良好的平衡性；而螺杆真空泵是在无油、干式的状态下运行，螺杆型线需要特殊处理，才能获得理想的工作性能，再考虑到制造成本因素，市场上以单头的螺杆真空泵为主，可以大幅节省加工时间而降低成本。伴随着干式螺杆真空泵高速化的发展趋势，有必要在设计阶段对螺杆转子进行动平衡优化设计计算，以提高螺杆泵整体工作性能的提高和使用寿命。

Thomas[2]提出了一种内压缩螺杆真空泵，螺杆采用连续渐变过渡形式，端面采用对称型线，该螺杆应用于德国Leybold的SrewLine系列螺杆式无油内压缩真空泵，是一种专门为工业应用设计的干式泵，解决了工业应用中，如粉尘、焦油等工况不好时的真空问题，其螺杆采用在吸气端减重，内部压缩比设计成3.5以上，螺杆才便于达到比较理想的动平衡，但是牺牲了半个压缩级数。North[3]设计了一种共轭锥形螺杆，其螺距保持不变，由轴向底径锥形变化引起内部压缩体积变化，该共轭锥形螺杆是英国Edwards针对恶劣真空环境推出的工业应用，采用平衡头[4-6]的方式达到螺杆的动平衡，但增加了螺杆轴向密封的难度。Ulrich[7]设计了一种平衡性能良好的变螺距双螺杆转子，端面型线保持不变，螺距由小到大，再到小，最后保持不变，这种螺杆应用于德国Busch公司的COBRA系列螺杆泵，制造工艺理想，自身能够达到85%以上的平衡，再辅助两个端面减重可达到完全平衡但是螺杆设计形式固定，缺乏变化。Zhang[8-9]研究了单头螺杆真空泵转子动平衡问题，提出了两个端面去质量，辅助齿顶面找正的动平衡方式，这种平衡方式破坏了齿顶表面结构，不能适应恶劣的工艺环境。

1问题提出

在实际操作过程中，最常见的螺杆转子动平衡方法是通过螺杆两个端面减重，再辅助螺杆齿顶端减重。在齿顶端减重所取的平衡孔或平衡槽，会带来两个后果，一方面，螺杆真空泵在运行过程中，污物会在平衡孔或槽的位置滞留，使螺杆的动平衡发生变化导致不平衡，引起机械振动，从而影响螺杆真空泵的运行性能和使用寿命；另一方面，由于平衡孔或平衡槽的存在，涂层不到位，特别在医药化工等有腐蚀的工艺的场合，减重平衡孔和平衡槽最易腐蚀。鉴于此，要设计既能适应恶劣工况，又有良好自身动平衡的螺杆，其转子的设计必须尽量保持螺杆齿顶结构表面的完整性，或设计的螺杆只需两端减除少许质量即可达到动平衡，使用寿命长，维护成本低。

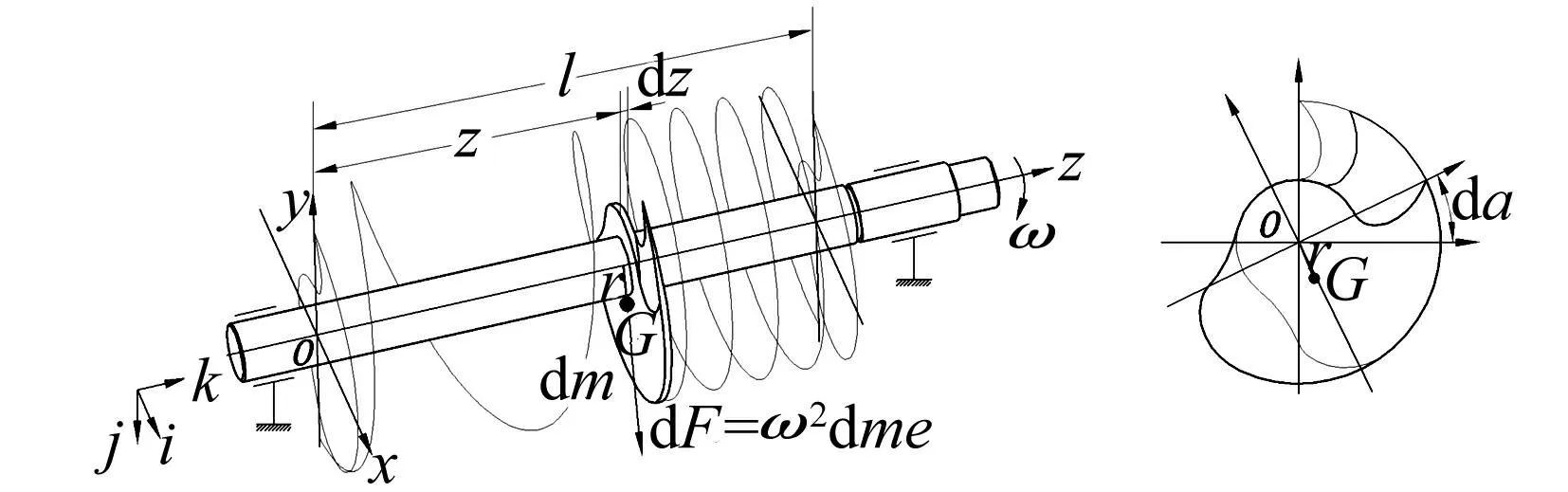
2螺杆转子模型

考虑到制造成本和互换性，绝大多数的螺杆真空泵的成对螺杆采用相同的端面型线，尺寸参数完成相同。端面型线不变的等导程螺杆转子动平衡的一般规律是：不论转子采用何种端面型线，当螺杆总长度等于其节距的整数倍，都能自动保证质心处于转动轴线上，从而满足静平衡要求。对于端面型线面积的形心不在转动轴线上，旋转时一定存在惯性力矩，无法满足动平衡条件，且转子长度越长(即螺旋导程数越多)，惯性力就会越大[9]。要使转子的惯性力矩尽可能小，则要求螺杆转子在任意两个指定平面上的质径积矢量和尽可能小，直至为零即满足平衡要求。内压缩的螺杆转子，是非等导程的螺杆转子，一般吸气端是大导程区域，排气端是小导程区域，不平衡量集中在大导程区域，因此螺杆整体设计采用三段式结构，作为排气端的尾部设计为等螺距的小导程，头部的吸气端和中间段采用变螺距，是起内压缩作用。吸气端螺距从小到大变化，中间段从大往小变化，两者相互作用减少不平衡量，结合文献[10]，螺杆转子设计成采用端面型线不变的变螺距螺杆转子。

2.1圆柱变螺距螺旋线

对于端面型线不变的螺杆转子，其轴向螺旋线是圆柱螺旋线Γ，可以表示为

(1)

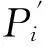
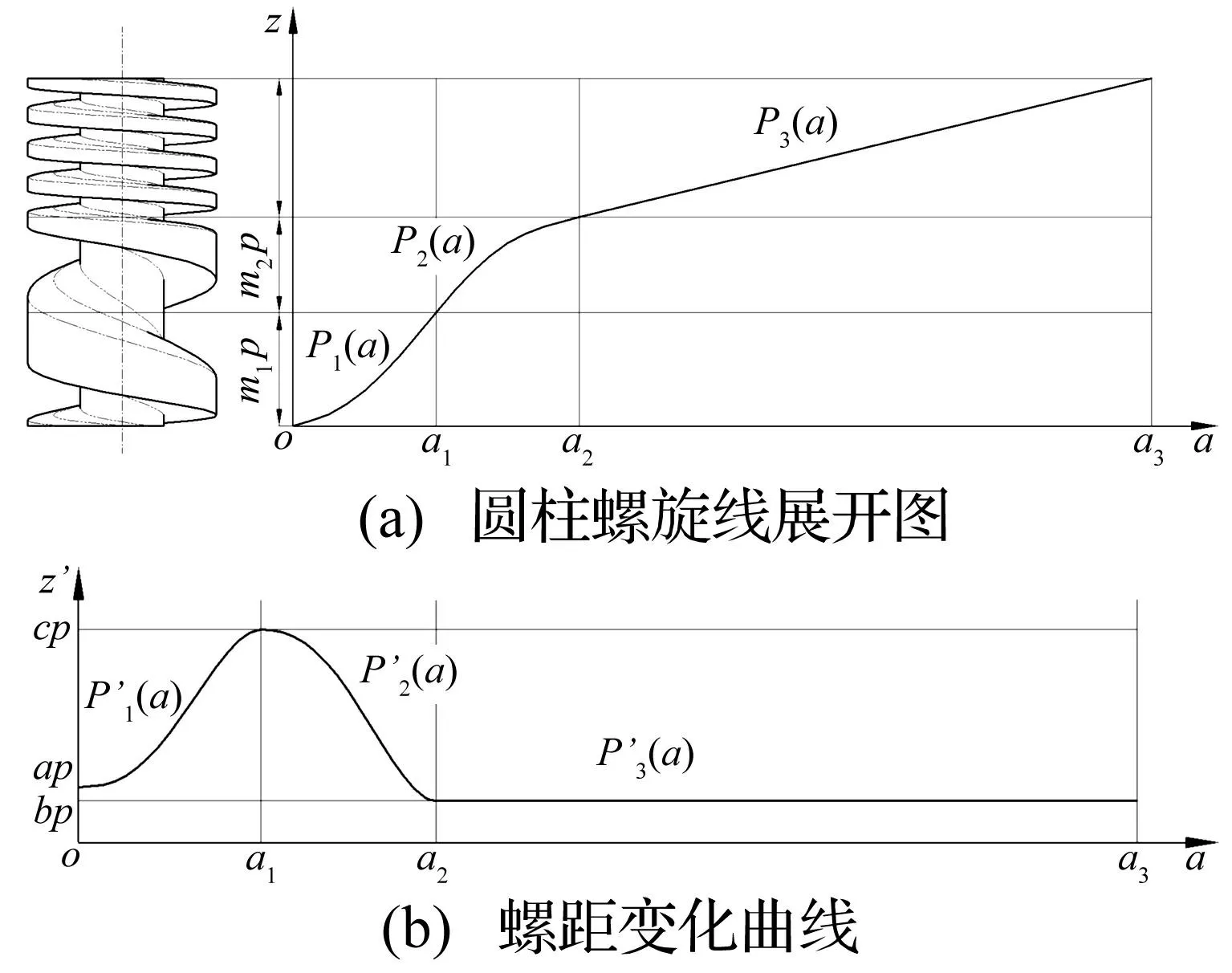
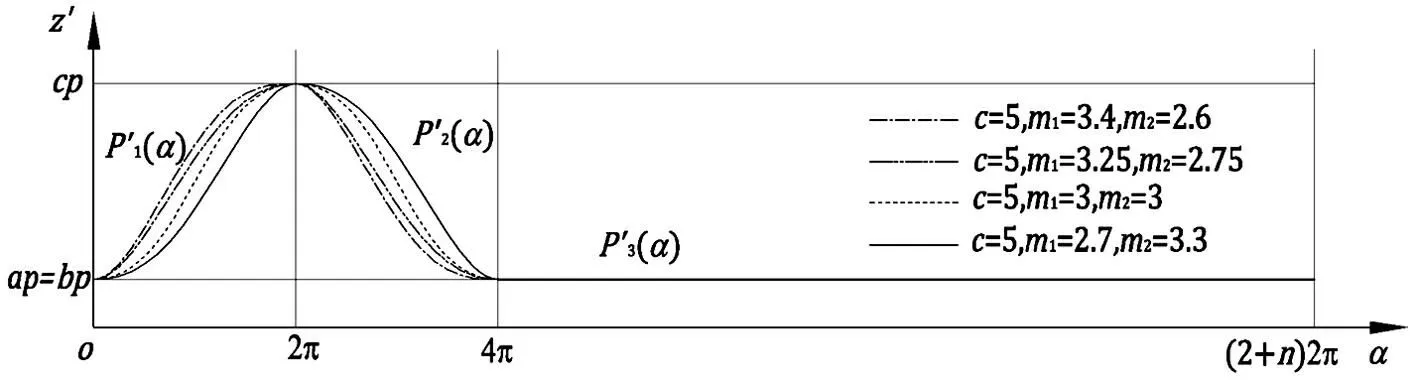
图1　渐变式圆柱螺旋线展开图、螺距变化曲线 Fig.1 Flat pattern of cylindrical Helix and variable pitch curve of cylinder spiral

图1中所示(P1(α)、P2(α)、P3(α))的三段圆柱螺旋线轴向参数方程分别满足：

P1(α1)=P2(α1)

P″1(α1)=P″2(α1)

P2(α2)=P3(α2)

P″2(α2)=P″3(α2)

(2)

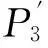
(3)

(4)

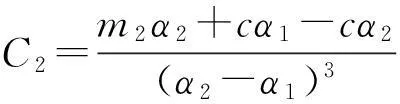
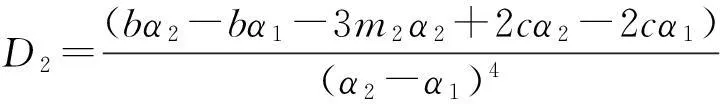
α2≤α≤α3

(5)

式(3)～(5)中，p为螺杆的最小螺距计算参考值；a为头部螺杆起始位置的变螺距参数；c为螺杆吸气端和螺杆中间段相交处的变螺距参数；b为排气端螺杆的等螺距参数，bp表示排气端螺杆导程；m1为吸气端变螺距参数，m1p表示该区域的轴向长度；m2为中间段变螺距参数，m2p表示区域的轴向长度。当b=1时，a,c分别表示螺杆内部体积相对于末端体积的压缩比。

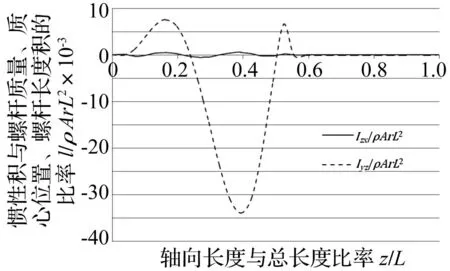
内压缩的螺杆真空泵压缩性能的改善，一个关键因素是如何优化设计内部压缩[12]，为此，当b=1时，为避免出现较小的螺距，须有1

(6)

(7)

(8)

考虑螺杆真空泵极限真空度等性能参数指标与简化计算，轴向整个导程数(级数)取值小于等于8；同时为取得良好的平衡性和减少螺杆级数，吸气端螺杆和中间段螺杆都为1个导程，即取α1=2π，α2=4π，α3=(2+n)×2π，n=0,1,2,3,4,5,6。

2.2变螺距螺杆三维精确实体模型

图2　三维啮合模型 Fig.2 3D meshed model

螺杆采用不变的端面型线，端面型线一边沿轴向移动，一边沿圆柱螺旋线转动，形成对应的螺杆，精确的三维实体啮合模型见图2。

3螺杆转子动平衡优化设计

3.1螺杆转子静、动平衡理论

螺杆转子为刚性转子，动平衡的条件要求通过转子质心的主惯性轴与旋转轴相重合。满足这一条件，旋转轴则不受任何力和力偶的作用，并且支承上没有动载荷作用，也就没有振动现象的出现，上述状态称之为完全动平衡状态。基于此，螺杆转子动平衡的设计指标是使转子的惯性力F和惯性力矩M尽可能小，最好同时为零。螺杆转子质量分布见图3。

图3　螺杆转子质量分布图 Fig.3 Mass distribution map of the screw rotor

图3中，dm为螺杆轴向长度的微量dz所对应的微小质量，ω是转子的固定转速，r型线面积形心与型线旋转中心的距离，G为微小厚度转子的质心，dα为微小厚度转子旋转的角度。惯性力F和惯性力矩M表示为[13]

F=ω2∫me→min

(9)

M=ω2k×(Izxi+Iyzj)→min

(10)

式(9)和式(10)中，∫m是螺杆转子总质量，e是螺杆转子质心与旋转轴心的偏移矢量，Izx是转子对Z-X轴的惯性张量，Iyz是转子对Y-Z轴的惯性张量，Izx和Iyz是度量转子的主惯性轴对旋转轴的倾斜角度的量。带入型线所包围的面积A和螺杆转子密度ρ，dm对应的惯性力dF为：

dF=ω2rdm=ω2rρAdz=ω2rρAp′(α)dα

(11)

代入面积A和密度ρ，F和M分量分别表示为：

Fx=ω2∑(∫(mrcosα)dα)=

ω2∑(∫(ρAp′(α)rcosα)dα)

(12)

Fy=ω2∑(∫(mrsinα)dα)=

ω2∑(∫(ρAp′(α)rsinα)dα)

(13)

Mx,z=ω2Izx=ω2∫zxdm=

(14)

My,z=ω2Iyz=ω2∫yzdm=

(15)

由于ρ,A,r和ω都是固定值，所以，式(12)～式(15)可分别写为：

(16)

(17)

(18)

(19)

式(16)～式(19)都是与螺旋线相关联的参数方程。

3.2设计变量

对螺杆的数学模型式(6)～(8)分析可知，决定螺杆几何参数有螺杆的最大压缩比c，排气端的导程数n，吸气端螺杆导程参数a和m1，中间段螺杆的导程参数m2，最小导程p和导程参数b。c决定了螺杆的压缩能力，n表示最终的螺杆压缩级数，m1和m2决定了螺杆的排气能力，螺杆的独立设计参数共7个，设计变量定义为：

X=(x1,x2,x3,x4,x5,x6,x7)T=

(a,b,c,n,m1,m2,p)T

(20)

3.3目标函数

为了达到理想动平衡状态，其设计指标是使转子的惯性力和惯性力矩尽可能小，该问题的目标函数可以表示为

(21)

优化的理想状态为四个分量均为零。

3.4约束条件

为了增加吸气端长度和简化模型计算，在优化设计过程中，吸气端和中间段约定为1个导程，排气端导程数约定为整数倍，总长度固定为L，最小导程

(22)

加上螺杆端面型线与总长度固定，从而总体积和重量固定，约束条件表示为

(23)

通过导程参数a,b,m1,m1,c的变化引起导程的变化，从而导致质量在轴向的重新分布。

至此，螺距螺杆转子动平衡计算的数学模型已经建立，这一计算模型和方法没有涉及转子型线的构成。

3.5优化计算及结果分析

由式(16)，式(17)可知，螺杆的静平衡条件为

(24)

现将不同Pi(α)的代入式(24)，则式(24)可写为

(25)

(26)

将式(6)～(8)代入上述两式，则式(25)和(26)分别可写为

(27)

(28)

由式(27)和(28)，可推导出

(29)

(30)

也就是说，式(3)～(8)中的螺杆设计参数，若满足条件(29)或式(30)，则螺杆转子可以达到静平衡。若b=1，p即表示排气端的导程，a,c表示内部体积压缩比(相对于排气端)。图4给出了相同的压缩比c，再给定初始的m1，得出符合静平衡条件的四种螺距曲线，图4中，不同的m1、m2值，从图中可以看出中间段螺杆的螺距曲线是由吸气端变形而得，排气端是等导程螺距曲线。

图4　符合静平衡条件的螺距曲线 Fig.4 pitch curves consist with static balance

再将式(3)～(8)代入动平衡条件式(18)和(19)，即可以得出方程

(31)

(32)

上述动平衡方程变量只涉及n,c,m1,m2四个变量，最终计算结果与L，p无关，n从固定的范围变化(0～6)，与方程式(27)，(28)联立，四个方程解四个未知数。

由方程式(31)，(32)可以推导出m1=m2，表明吸气端和中间段螺距曲线对称，不同的n之下，压缩比等各参数的变化见表1。

表1　满足动平衡的参数

m1和m2不相等时，螺距曲线变形较多，当m1和m2数值比较接近时，不平衡量比较小，第三和第四个分目标函数的数值就可以取得最小值，再借助两端减重来达到理想的动平衡；m1/m2比值相差不要太大，建议取值0.8～1.2之间，这样动平衡量减重比较小。图5是表1中n=6的螺杆质心轴向变化规律，rx,ry,r分别是螺杆质心x,y分量和合成值沿螺杆轴向变化的规律，从图中可以看出螺杆吸气端和中间段质心位置变化比较明显，沿着螺杆轴向逐渐变小，到排气端时，质心在较小的范围内规律性的波动。在螺杆设计计算过程中，m1和m2不相等时，压缩比固定的情况下，m1取较大值，吸气段螺杆比中间压缩段螺杆长，可以提高抽气速率；m2取较大值，中间压缩段螺杆长度变长，压缩更平稳，因此可以根据具体工况选取设计参数，产生的不平衡量可以在两端减重。

图5　螺杆质心轴向变化规律 Fig.5 Variable rule along axis of centroid of screw rotor

图6是表1中n=6的螺杆惯量积轴向变化规律，图中ρAL的积为螺杆质量，从图中可以看出，Iyz波动较大，Izx波动很小，到排气端小导程等螺距区域两种变化都很小，可以看出吸气端和中间段的螺杆设计抵消了绝大部分的不平衡量。

图6　螺杆惯量积轴向变化规律 Fig.6 Variable rule along axis of inertia of screw rotor

3.6设计实例与试验

以螺杆LG50为例，螺杆长度L=306mm，图7(a)是n=3，c=5.5614完全动平衡设计；图7(b)是n=6，c=6.4842完全动平衡设计；图7(c)固定压缩比c=5，n=3的设计实例，这种设计有少许的不平衡量产生，为保证螺杆齿顶表面的完整性，需要两端面减重，只需去除少许重量即可，图示实例两端减重35.1g。

图7　设计实例 Fig.7 design examples

使用Pro/engineer行为建模技术，得到图7(a)设计实例的质量属性，见图8，惯性积Izx和Iyz都为零。

图8　设计实例的质量属性(n=6) Fig.8 Mass attribute of design examples(n=6)

动平衡试验使用上海申克的硬支承平衡机，型号YYW-300A，螺杆设计阶段已经具有良好的动平衡，不平衡量主要由加工、材质的不均匀引起，总体的不平衡量很小，实际测量值左端0.653g，右端1.71g，符合ISO1940动平衡标准。在转速更高或动平衡要求更高的情况下，为了让螺杆真空泵能够适应恶劣的工作环境，只需在两端去除少许重量，动平衡现场见图9。

图9　动平衡试验 Fig.9 Dynamic balancing test

4结论

设计了一种可以表面结构完整、适应恶劣工况的内压缩螺杆真空泵自平衡螺杆转子，螺杆转子无需齿顶减重即可以达到自身良好的动平衡，可保持螺杆齿顶表面的完整性，提高螺杆真空泵的使用寿命。构建的螺杆转子动平衡计算与优化方法，在螺杆端面型线不变的情况下，螺杆的静、动平衡设计只与螺距曲线和缠绕角度有关联，和具体的端面型线参数、螺杆长度无关。使用文中方法设计的螺杆转子，在级数一定的情况下达到动平衡时，压缩比是固定值；在压缩比固定的情况下，级数越多，动平衡越好，通过在两个端面减重达到了完全动平衡。

参考文献

[1]郭蓓，薛建国，牛瑞，等．干式螺杆真空泵研究现状与展望[J].真空，2009，46(5)：37-40．

GUO Bei, XUE Jian-guo, NIU Rui, et al. Current situation and outlook for R&D of dry screw vacuum pumps[J].Vacuum, 2009, 46(5)：37-40．

[2]Thomas D,Magnus J,Peter B, et al. Screw Vacuum Pump: DE, DE102010019402[P]. 2010-05-04.

[3]North M H,Turner N, Davenne T R G, et al. Screw pump, GB0912208D0[P].2009-08-26.

[4]樊红卫，景敏卿，王仁超，等.一种电磁式自动平衡头设计计算与响应试验[J].振动、测试与诊断,2014,5(10)：807-811.

FAN Hong-wei, JING Ming-qing, WANG Ren-chao, et al.Design, calculation and response experiment of an automatic electromagnetic balancer[J].Journal of Vibration, Measurement & Diagnosis,2014,5(10)：807-811.

[5]王维民，高金吉，江志农，等.旋转机械无试重现场动平衡原理与应用[J].振动与冲击,2010,29(2)：212-215.

WANG Weimin, GAO Jinji, JIANG Zhinong,et al. Principle and application of no trial weight field balancing for a rotating machinery[J]. Journal of Vibration and Shock, 2010,29(2)：212-215.

[6]顾超华，曾胜，罗迪威，等.一种机械式在线平衡头的设计与实验研究[J].振动与冲击,2014,33(12)：151-155.

GU Chao-hua，ZENG Sheng，LUO Di-wei, et al. Design and tests for a mechanical type of online balancing actuator[J]. Journal of Vibration and Shock,2014,33(12)：151-155.

[7]Becher Ulrich.Twin screw rotors and displacement machines containing the same,WO0208609A1 [P].2002.

[8]Zhang Shi-wei, Gu Zhong-hua, Zhang Zhi-jun. Dynamic balancing method for the single-threaded, fixed-pitch screw rotor[J].Vacuum, 2013,90:44-49.

[9]顾中华，张世伟，张志军.无油螺杆真空泵单头等螺距转子的动平衡计算[J].真空,2011,48(6): 46-50.

GU Zhong-hua, ZHANG Shi-wei, ZHANG Zhi-jun. Dynamic balance calculation of the single-threaded and fixed pitch rotor in dry screw vacuum pump[J].Vacuum,2011,48(6): 46-50.

[10]巫修海.一种干式螺杆真空泵变螺距螺杆:中国,102937094A[P].2013-02-20.

[11]孙志忠，袁慰平，闻震初.数值分析[M].南京:东南大学出版社，2002.

[12]Pfaller D，Brümmer A，Kauder K．Optimized rotor pitch distributions for screw spindle vacuum pumps [J] ．Vacuum， 2011，(85) ：1152-1155．

[13]三轮修三，下村玄.旋转机械的平衡[M].北京:机械工业出版社,1992,6-9.

第一作者包兴先男，博士，讲师，1981年11月生

第一作者仲健林男，博士生，1988年生

通信作者任杰男，讲师，1982年生