Gauss白噪声参激下悬挂轮对系统的随机稳定性研究
Gauss白噪声参激下悬挂轮对系统的随机稳定性研究
张波,曾京,刘伟渭
(西南交通大学牵引动力国家重点实验室,成都610031)
摘要:在非线性悬挂轮对系统中加入了Gauss白噪声参激,通过Hamilton系统理论和随机微分方程理论,将系统转化为拟不可积Hamilton系统伊藤随机微分方程组,根据拟不可积Hamilton系统的随机平均法,把该方程组降维为一维扩散的平均伊藤随机微分方程,使原系统的解依概率收敛到一维伊藤扩散过程。通过分析一维扩散奇异边界的性态得到了随机全局稳定性的条件。最后对系统的D分叉和P分叉行为进行了研究,并画出了随机P分叉图和随机极限环图。结果表明,随机项的作用使系统的临界速度发生漂移,随着噪声项强度增大,临界速度显著降低。P分叉后系统表现为最大可能意义上的随机极限环振荡,而D分叉后统表现为概率1意义下不稳定的非极限环随机振荡。
关键词:随机平均法;奇异边界;随机P分叉图;随机极限环图
中图分类号:U271.91
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.19.008
Abstract:Here, Gauss-White-noise parametric random excitation was input in a nonlinear suspended wheelset system. According to Hamilton system and the stochastic differential equation theory, the system could be expressed as a quasi-non-integrable Hamiltonian system in form of Ito stochastic differential equation. The equation was reduced to one dimensional diffusion Ito average stochastic differential equations with the stochastic averaging method. So, the solution to the original system converged in probability an one-dimensional Ito diffusion process. The global stochastic stability conditions were obtained by analyzing the modality of the singular boundary of the one-dimensional diffusion. At last, the stochastic P-bifurcation and D-bifurcation behaviors of the system were studied. The stochastic P-bifurcation diagram and the stochastic limit cycle one were plotted. The results showed that the random excitation can drift forward the system critical speed and the system critical speed significantly decreases when the intensity of random excitation increases; the P-bifurcation leads to the most possible limit cycle of the system, while the D-bifurcation leads to an unstable non-limit cycle of the system in the sense of probability 1.
基金项目:总装备部武器装备预研基金(9140A27020212JB14311)
收稿日期:2014-08-20修改稿收到日期:2014-09-30
Stochastic stability of a suspended wheelset system under gauss white noise
ZHANGBo,ZENGJing,LIUWei-wei(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)
Key words:stochastic averaging method; singular boundary; stochastic P-bifurcation diagram; stochastic limit cycle diagram
铁道车辆系统的蛇行运动稳定性是轮轨系统本身的固有属性。铁路车辆运行速度的提高使车辆动力学研究变得十分重要。
在以往的研究中,许多学者对车辆系统的稳定性进行了大量深入的研究,并形成了较为完整的轨道车辆系统力学[1-2],对蛇行运动的研究历史也可追忆到1个多世纪以前的Stephenson,车辆系统横向运动稳定性的研究经历了一个由线性到非线性的过程。不同的研究人员建立了许多线性的、非线性的系统模型,并针对这些模型提出了具体的定量或定性的方法,同时建立了较为完整和丰富的轨道车辆稳定性和分岔理论,这些理论对提高和保障车辆的运行性能起到了巨大作用。这些研究都是在确定性系统框架内进行的,但随着铁道车辆的快速发展,运营速度的不断提高,对车辆系统稳定性提出了更高的要求,这就需要研究车辆系统在受外界随机激励和结构自身参数随机因素影响下的随机稳定性问题。
轨道车辆系统中随机噪声扰动和结构自身参数随机影响是不可避免的,这些因素经常使得系统呈现出随机性、不确定性,确定性系统模型只是实际系统的理想化,因此随机系统对自然规律的描述更本质和真实。在这种情况下,确定的系统模型已经无法反映现实系统运动的真实行为,也不能满足理论发展的需要。许多研究表明,由于噪声与非线性的相互作用,往往使噪声对系统的演化起着决定性的作用,这种作用有时可能导致系统结构的完全损坏,使系统行为从有序变为无序,有时可能起积极作用,使系统的行为从无序变为有序。深入认识非线性随机现象的内在机理、运动形态,掌握其内在规律,并在此基础上加以控制,使其朝有利的方向发展,无疑是一项具有重要科学意义和实际指导价值的研究。
刘伟渭等[3]对弹性轮对随机稳定性进行了研究,其通过李亚普诺夫指数和奇异边界理论分析了全局随机稳定性和局部随机稳定性,但研究过程中只是简单涉及随机分叉,并未对随机分叉问题进行深入分析。同时考虑到车辆高速运行时,轮动陀螺效应不可忽视[4],本文将轮对陀螺力引入悬挂轮对系统,考虑悬挂刚度参数随机激扰,分析随机项对系统的影响,并对系统随机分叉行为进行较深入研究。
1轮对系统随机模型的建立
车辆系统为复杂多体系统,其非线性问题比较复杂,而随机非线性问题的复杂度相较一般非线性系统的复杂度大大提升,如果直接研究整车系统的随机动力学问题将会非常困难,因此本文不考虑转向架和车体蛇形,采用简化的轮对模型来进行理论分析。
为此,本文建立了悬挂轮对系统摇头和横移耦合的随机几何模型(图1),模型中考虑了悬挂元件的制造公差、材料老化以及材料不均质等问题对悬挂刚度的随机影响,将悬挂刚度的随机影响简化为高斯白噪声随机过程ζ(t)。车辆系统中基本包含三类非线性环节:非线性轮轨接触关系、非线性蠕滑特性和非线性车辆悬挂特性,非线性蠕滑特性一般可近似认为是线性的,非线性悬挂特性一般主要体现在二系悬挂(比如抗蛇行减振器、二系空簧等),但在一系悬挂中非线性因素相对影响较小,本文悬挂轮对系统中主要考虑一系悬挂,故非线性悬挂特性也可不做考虑,因此非线性项主要体现轮轨非线性接触关系,系数α1和α2的选取参考文献[5]。考虑轮对陀螺力,轮对的随机运动方程[5]为
(1)
式中,y为轮对横移量,φ为轮对摇头角,m为轮对质量,I3为轮对摇头转动惯量,r0为滚动圆半径,a为两滚动圆间的距离之半,L为左右悬挂跨距之半,λe为踏面等效锥度,kx和ky为轮对横向和纵向定位刚度,fij为Kalker蠕滑系数,W为轴重,β1,β2为随机项控制参数,ζ(t)为均值为0强度为2D的高斯白噪声随机过程,相关函数为:
E[ζ(t)ζ(t+τ)]=2Dδ(τ)
(2)
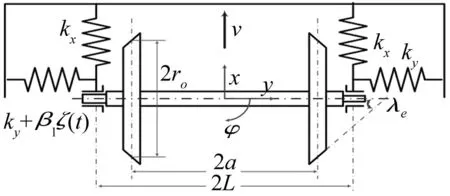
图1 悬挂轮对的随机几何模型 Fig.1 Dynamic model of suspended wheelset system
(3)
式中,
(4)
设系统的Hamilton函数为:
(5)
(6)

(7)
2轮对系统的随机平均和全局稳定性
2.1轮对系统的随机平均
随机平均法实际上是KBM渐近法在随机系统中的一个推广。它的理论依据是满足所谓“强混合条件”和弱紧性条件的随机系统的一个极限定理[6]。朱位秋[7]在此基础上建立了拟Hamilton系统的随机平均法理论,形成了非线性随机动力学与控制的Hmailton理论体系框架,为解决随机激励下多自由度非线性系统的响应、稳定性、分岔、可靠性、与控制等问题提供了一个十分有效的新途径。
在随机分岔研究过程中,随机平均法有着很重要的作用。使用随机平均法能使原系统降维、简化,而同时保持有原系统的主要非线性特性,特别是所得慢变过程为扩散过程,其扩散矩阵是非退化的,从而更适宜于研究非线性系统的随机稳定性、随机分岔、首次穿越、以及随机最优控制等问题。

dH=m(H)dt+σ(H)dB(t)
(8)
式中,B(t)为Weiner增量过程,m(H)和σ(H)为别为一为扩散过程H(t)的漂移系数和扩散系数,经积分计算可得:
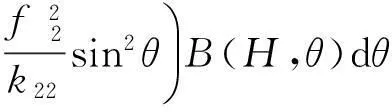
(9)
式中:
(10)
式中,R是区域Ω′的边界方程之解,即R满足:

(11)
2.2轮对随机系统的全局稳定性
经过随机平均,系统(3)依概率收敛到一维扩散过程H(t)。对于扩散过程H(t),其概率渐近稳定性与其平稳概率密度的存在性可以完全由该过程在边界上的性态确定。因此下面主要分析扩散过程H(t)的两个边界性态:左边界H→0和右边界H→∞。
对于右边界,当H→∞时,H应对应R的高次项,对(11)式关于θ求期望,得:
(12)
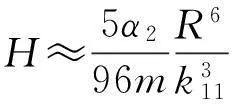
αR=4/3,βR=1
(13)

对于左边界,当H→0时,可得σ2(H)→0,m(H)→0,属于第一类奇异边界且H→0为套点,漂移系数和扩散系数渐近的收敛于下面的两式:
(14)
相应的,判断边界类别的扩散指数αL(下标L表示左边界)、漂移指数βL以及特征标值cL分别为:
αL=2,βL=1
(15)
下面讨论参数对系统全局稳定性的影响,当cL<1时,左边界H→0是吸引自然边界,右边界H→∞排斥,系统的解曲线会在整个能量域上趋向左边界,也就是能量趋向0附近,所以此时系统平凡解是全局稳定的。
相反,当cL>1时,左边界是排斥自然边界,左右边界都是排斥自然边界,系统的解曲线会在能量域上往返,最终会稳定在(0,∞)区间上的某个稳态能量处(图5)。所以此时系统平凡解是不稳定的。其具体的稳态位置需要求解系统的FPK方程,可知其能量稳态概率密度函数。

图2 轮对随机系统全局稳定性示意图 Fig.2 The global stochastic stability of wheelset
当cL=1时,为系统临界状态,由式(15)可得:
(16)
若取噪声强度D=0.05将附录参数表1代入方程 (16),可知当速度小于58.6m/s时,系统在概率意义上全局稳定;当速度超过58.6m/s时,系统在概率意义上失稳,轮对可能出现蛇形失稳。
一旦系统失稳,系统的拓扑结构将随着系统参数的改变而发生定性改变,即发生分岔。下面将具体分析系统在随机激励下的随机分叉。
3随机分叉
所谓随机分叉,则是指由参数的随机扰动引起的动态系统的定性性质(稳定性、拓扑结构)的变化[10]。描述随机系统的动态性质的量有很多,例如最大Lyapunov指数、稳态概率密度、响应的矩等,不妨将这些量称为特征量,故根据不同特征量得出的随机分叉点可能是不同的。
目前随机分叉主要有两种形式[10-11]:动态分叉(D分叉)与唯象分叉(P分叉)。D分岔是研究从一族参考测度中分岔出新的不变测度,可用 Lyapunov 指数的正负来判别;P-分岔则是研究随机动力系统不变测度的密度及其形状随参数的变化,可从峰的个数、位置及形状来辨别。D -分岔是一种动态概念,它与确定性分岔相对应,当噪声强度趋于零时,D 分岔退化为确定性分岔。 P 分岔则是一种静态概念。 D 分岔与P 分岔之间一般无关系,即D 分岔并不意味着P 分岔,反之亦然。
3.1随机D分叉

dH=m′(0)dt+σ′(0)dB(t)
(17)
解得:
(18)
[m′(0)-(σ′(0))2/2]/2
(19)
当H→0时,H应对应R的低次项,由于R满足式(11),对(11)式R的低次项部分关于θ求期望,可知
(20)
即R2=2H,则有:
(21)
则最大Lyapunov指数为:
(22)
当λ<0,说明系统总能量会随着运行时间的增加逐渐减小,也就是说,此时系统的能量增加能力小于能量消耗能力,系统会逐渐收敛于平衡位置而稳定,λ越小能量减小得越快,系统也越稳定。
当λ>0,说明此时系统能量增加能力大于能量消耗能力,随着运行时间延长,系统总能量会逐渐积蓄,该部分能量逐渐转换为系统动能和势能,并发生失稳行为。λ越大能量积蓄越快,失稳也越严重,当增加能量达到系统储存极限时,系统将失效并发生脱轨行为。
当λ=0,系统处于失稳与稳定临界状态,系统发生D分叉。
根据附录参数表1可得最大Lyapunov指数的三维图和等势图,见图3和图4。

图3 最大Lyapounov指数三维图 Fig.3 The 3D map of the Lyapounov exponent

图4 最大Lyapounov指数等势图 Fig.4 The isopotential map of the Lyapounov exponent
从图3和图4看出,Lyapunov最大指数随着运行速度V和噪声强度D的增加而增加,随着速度和噪声强度的增大,最大Lyapunov指数逐渐增大,当两者达到一定值后,最大Lyapunov指数会由负变正,即系统由稳定变为不稳定,系统发生D分叉。
图5为不同噪声强度下,最大Lyapunov最大指数随速度变化图,当λmax=0时,出现D分叉临界点,对应的速度为D分叉临界速度,当噪声强度D=0.05时,可得VD=58.6m/s。
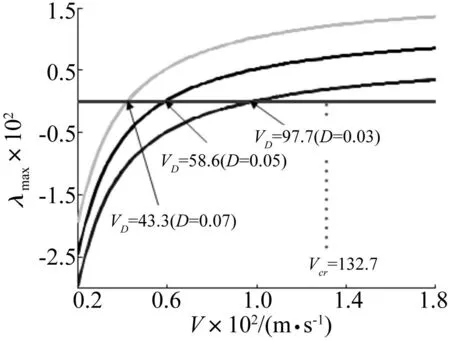
图5 最大Lyapounov指数随速度变化图 Fig.5 The Lyapounov exponent vary with the speed
随着噪声强度D增大,D分叉临界速度显著变小。当D→0时,D分叉临界速度逼近对应的确定性系统非线性临界速度Vcr=132.7m/s[5],D 分岔退化为确定性分岔。
综上所述,考虑结构自身随机因素后,系统临界速度发生了较大变化,噪声项的作用使系统的临界速度发生漂移,随着噪声项强度增大,临界速度显著降低。随机激励使系统发生D 分岔,分叉前系统表现为概率1意义下的稳定运动;分叉后系统表现为概率1意义下不稳定的非极限环随机振荡,其具体体现形式有待进一步深入研究。
3.2随机P分叉
在随机动力系统中,所谓的P分叉[11]就是随机动力系统概率密度函数的形状随系统参数发生实质变化,P分叉点是非概率1意义的,是对应于某一概率值的随机分叉。导致这一现象的主要原因是由于随机系统的多样本的复杂特性,其随机分叉现象的发生也会因此对应有多个概率值。
由拟不可积Hamilton系统的随机平均[9]可知,一位扩散过程H(t)的FPK方程满足如下形式:
(23)
对于系统的FPK方程(25)而言,我们感兴趣的是响应的稳态解,即转移概率密度的定常解。FPK 方程(25)一般需数值求解,但它的平稳解极易求出:
(24)
式中,C为归一化系数。
当H→0时,省略方程(19)中的高阶项,代入方程(26),可得:
p(H)=CHηexp(-aH-bH2)
(25)
其中,
(26)
在平衡点附近,漂移系数m(H)和扩散系数σ2(H)可以表示为:
m(H)=O(HβL),βL≥0
σ2(H)=O(HαL),αL≥0
(27)
则稳态概率密度可改写为:
(28)
当βL-αL=-1且H→0时,
p(H)=O{H-αLexp[cLlnH]}=
O{HcL-αL}=O{Hη}
(29)
当η<1时,p(H)是一个δ函数;当1<η< 0时,p(H)是一个减函数且在原点处取得最大值,发生第一次分岔;当η> 0时,p(H)仍会取得最大值,但最大值位置远离原点,此时发生第二次分岔。于是,在η=1时发生随机D-分岔,(意义类似与确定性系统分岔)在η= 0时发生随机P-分岔(概率密度函数的形状变化),这两次分岔构成了随机Hopf分岔。
根据附录参数表1,由η=0可得,随机P-分岔临界速度为VP=117.2m/s。当η=1时,随机D-分岔临界速度为VD=58.6m/s,与3.1节计算结果吻合。

当速度增大时,系统的稳态能量概率密度函数的图形形状发生了变化。稳态概率密度函数的峰值的位置表示发生分岔的对应系统广义能量值,峰值的高度代表概率的大小。见图6,当速度为50m/s时,稳态能量概率密度函数图是一个δ函数,在能量0处概率趋近无穷,其他位置几乎处处为零;当速度为110m/s时,p(H)是在H=0处有最大值的减函数;当速度为170m/s时,p(H)在H>0处有最大值,最大值处对应的能量值H表示发生分岔的对应系统广义能量值。且随着速度进一步增加,系统发生分岔的概率最大对应的能量值H也变大,对应的峰值降低。
由图7知,当速度逐渐增大后,系统的联合概率密度图会从单峰渐渐变成“火山口”,且随着速度进一步增加,“火山口”形状将越来越明显,对应的峰值降低。
由图8知,当速度逐渐增大后,系统的边缘概率密度ps(y)会从单峰渐渐变成双峰,且随着速度进一步增加,双峰会越来越分离,对应的峰值也逐渐降低。
系统广义位移与系统广义动量的联合平稳概率密度表达式为:

(30)
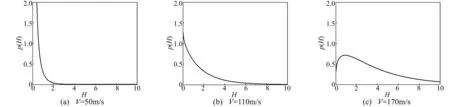
图6 稳态能量概率密度图(D=0.05) Fig.6 Stationary energy probability density (D=0.05)

图7 横移和摇头稳态联合概率密度图(D=0.05) Fig.7 Joint stationary probability density of displacement and velocity (D=0.05)
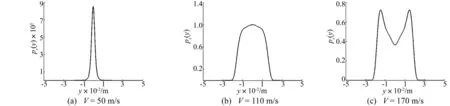
图8 横移稳态边缘概率密度图(D=0.05) Fig.8 Marginal probability density with respect to the lateral displacement (D=0.05)
下面研究边缘概率密度函数ps(y)的极值情况.概率密度函数的极值具有重要的意义[10],这是由于:
①极值点的个数与位置是最显著的特征之一,Namachchivaya认为它含有非线性随机系统稳态行为的“最根本”的信息。②作为确定系统稳态行为的推广,当噪声的强度趋近于零时,极值趋近于表现确定系统的稳态行为。③极大值表示样本轨线在此点停留较多时间,因而定常解是稳定的;而极小值则标志轨线在此点停留较少时间,是不稳定的。这个原理与离出问题对稳定性的判别相似。
对于悬挂轮对随机系统,轮对横移量最大概率出现的振幅y*由ps(y)的极大值问题决定:
(31)
利用方程(31)可得系统的轮对横移最大可能振幅随机P分叉图,见图9。

图9 轮对横移最大可能振幅随机P分叉图(D=0.05) Fig.9 P-bifurcation diagram of the most probable lateral displacement amplitude(D=0.05)
由图9可见,随机噪声项的介入使系统的分叉点发生漂移,临界速度变低。当速度V=130m/s时,可得系统对应的相空间中的极限环图,见图10。

图10 轮对横移随机极限环图(D=0.05, V=130) Fig.10 The stochastic limit cycleof the lateral displacement (D=0.05, V=130)
由图10可知,当分叉参数跨过P分叉点后,由于噪声的介入,对应的确定Hopf分叉系统中的极限环变成一个边界模糊的“随机极限圈”,包括一系列不同的可能极限环,各个可能的极限环出现的概率不同。在其中存在一个概率最大的极限环,其对应到图中为颜色最深的极限环,说明当轮对运行速度V=130m/s时,系统最可能最终在横移量为8mm的极限环上发生蛇形晃动,与轮对横移最大可能振幅随机P分叉图结果吻合。
随机系统产生的分岔行为与确定系统产生的分岔行为是不同的,随机系统由于受到随机因素的作用,当满足一定的条件时,系统发生的分岔是以一定的概率形式来反映的,一方面,这说明即使满足一定的分岔条件,分岔也并不是一定会产生,发生分岔的概率反映了发生分岔的可能性的大小,可见随机系统的复杂性,无法作出确定性的预测;另一方面,系统参数发生变化时,发生分岔的概率也发生相应的变化,可通过调节系统参数,改变分岔产生的概率。
通过具体分析,我们分析了轮对运行速度对随机分岔的影响,当稳态概率密度出现火山口时即可判定发生随机P分岔,随机 P分岔的产生会导致轮对系统发生蛇形晃动,蛇形晃动的极限环幅值服从一定的概率分布,此时存在最大可能意义上的随机极限环振荡,可能导致系统失稳甚至脱轨。由于车辆在运行过程中,不可避免受到各种随机因素的影响,且一旦激扰强度较大,系统稳定性显著变差,出现较大安全问题,因此为避免随机P分岔的产生,系统运行速度应远离分叉点,留下一定的安全余量,以降低发生随机P分岔的危险。
4结论
白噪声参激下悬挂轮对系统的随机动力学行为将会比确定性Hopf分叉更为复杂。通过最大Lyapunov指数、一维扩散边界和FPK方程的考察获得了以下主要结论:
随机因素对系统平衡点的稳定性影响很大,甚至决定系统的分岔值。考虑结构自身随机因素后,系统临界速度发生了较大变化,噪声项的作用使系统的临界速度发生漂移,随着噪声项强度增大,临界速度显著降低。
受白噪声激励的影响,系统产生了2个分叉点,第1个是概率1意义上的D-分叉点,系统概率1意义下失稳;第2个是P-分叉点,产生最大可能意义上的随机极限环振荡。从而导致系统出现3种不同随机动力学行为:概率1意义下的稳定运动、概率1意义下不稳定的非极限环随机振荡和最大可能意义上的随机极限环振荡。对于受白噪声激励的轮对系统,其概率1意义的随机振动和最大可能意义上的随机极限环振荡这两种动力学行为和确定性蛇形运动基本类似。但是概率1意义下不稳定的非极限环随机振荡这种动力学行为只存在于受随机激励的系统中,在确定性非线性分析中不存在这种动力学行为,这种动力学行为主要是由系统的非线性和随机因素共同作用而产生的。
不同随机强度下的轮对系统有着不同的失稳临界速度,这和不能考虑随机因素作用下的确定性轮对系统只有一个确定的失稳临界速度有着本质区别。这也为确定性系统框架下无法解释的轨道车辆在不同线路等级条件下拥有不同的失稳临界速度提供了理论解释。
车辆在实际运行中总会受到结构自身随机因素的作用,考虑随机因素后的轮对失稳临界速度更能反映系统的真实运动行为,这些随机因素都是弱随机因素,一般情况下噪声强度D较小,系统的临界速度会发生漂移但不会漂移过大,这与实际车辆运行情况是一致的。
参考文献
[1]刘宏友.高速列车中的关键动力学问题研究[D].成都:西南交通大学,2003.
[2]曾京. 车辆系统的蛇行运动分叉及极限环的数值计算[J]. 铁道学报,1996,(3): 13-19.
ZENG Jing. Numerical computations of the hunting bifurcation and limit cycles for railway vehicle dydtem [J].Journal of the China Railway Society,1996,(3): 13-19.
[3]刘伟渭,戴焕云,曾京.弹性约束轮对系统的随机稳定性研究[J]. 中国机械工程,2013,24(6):799-804.
LIU Wei-wei, DAI Huan-yun, ZENG Jing.Research on stochastic stability of elastic constraint wheelset system [J]. China Mechanical Engineering, 2013,24(6):799-804.
[4]黄世凯.轮对运动稳定性的机理研究[D]. 成都:西南交通大学,2013.
[5]Khasminskii R Z. A limit theorem for the solutions ofdifferential equations with random right-hand sides[J]. Theory of Probability and Application, 1966, 11: 390-405.
[6]Von Wagner U. Nonlinear dynamic behaviour of arailway wheelset[J]. Vehicle System Dynamics,2009, 47(5): 627-640
[7]朱位秋.几类非线性系统对白噪声参激与(或)外激平稳响应的精确解[J]. 应用数学和力学,1990,11 (2):155-164.
ZHU Wei-qiu. Exact solutions for stationary responses of several classes of nonlinear systems to parametric and/or external white noise excitations [J]. Applied Mathematics and Mechanics, 1990,11(2) :155-164.
[8]Zhu W Q,Yang Y Q. Stochastic averaging of quasi-non-integrable hamilton system[J].ASME Journal of Applied Mechanics,1997,64:157-164.
[9]朱位秋,非线性随机动力学与控制-Hamilton 理论体系框架[M]. 北京:科学出版社,2003.
[10]刘先斌,陈虬,陈大鹏. 非线性随机动力系统的稳定性和分岔研究[J].力学进展, 1996,26(4):437-452.
LIU Xian-bin, CHEN Qiu, CHEN Da-peng. Study on stability and bifurcation of nonlinear stochastic Dynamic system [J]. Advances in mechanics,1996,26(4):437-452.
[11]葛根. 矩形薄板振动的随机分岔和可靠性研究[D]. 天津:天津大学,2009.
附录

表1 轮对系统参数表

第一作者戴豪民男,博士生,1982年5月生
通信作者许爱强男,博士,教授,博士生导师,1963年9月生

