高速列车表面压力测试信号的振动干扰分离研究

高速列车表面压力测试信号的振动干扰分离研究

何洪阳， 陈春俊， 缪晓郎， 何发胜

(西南交通大学机械工程学院，成都610031)

摘要：高速列车表面压力测试过程中，压阻式绝压传感器受列车振动冲击激扰，引起传感器输出干扰；同时，车体振动又会引起表面压力变化，导致有用信号与干扰信号难于准确分离。针对现有的经验模态分解(EMD)降噪过程中存在端点效应和模态混叠现象，提出了一种改进的集合经验模态分解(IEEMD)，并利用仿真信号进行验证。模型车在单自由度方向振动激励下，运用IEEMD方法对车体表面压力信号进行经验模态分解，再计算各固有模态函数(IMFs)分量自相关函数与原始信号自相关函数的相关性系数，提取振动引起的压力。同时利用CFD计算模型车在同一激励下振动压力，从而分离出振动干扰，并建立振动与振动干扰的回归关系，为准确提取列车表面压力提供理论指导。

关键词：高速列车；表面压力；振动干扰；改进EEMD

中图分类号:U270.1;TP274

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.011

Abstract:Piezoresistive pressure sensors are affected by shock and vibration when measuring surface pressure of a high-speed train, sensors’ output interference is caused. Simultaneously, the train body’s vibration causes the change of its surface pressure to lead to useful signals being difficult to separate from interferences. Aiming at the phenomena of end effects and mode mixing in process of noise reduction of the empirical mode decomposition (EMD), an improved ensemble empirical mode decomposition (IEEMD) method was put forward and it was verified with simulated signals. The model-train was excited with a single DOF vibration excitation. The train surface pressure signal was decomposed with IEEMD, and the correlation coefficients between the intrinsic mode function (IMF) autocorrelation functions and the original signal autocorrelation function were calculated. Then, the pressure caused by vibration was tracted. At the same time, the vibration pressure of the model-train surface was calculated with CFD under the same excitation, through comparing these presure data the vibration interference could be separated. The regression relationship between vibration and vibration interference was built to provide a theoretical guidance for extracting surface pressure accurately.

基金项目：国家自然科学基金项目(51475287)；国家自然科学基金项目(11272214)；国家高技术研究发展计划(863)项目(2012AA01A307) 国家自然科学基金(51278511)

收稿日期：2014-05-07修改稿收到日期：2014-09-25 2014-07-09修改稿收到日期：2014-10-17

Vibration interference separation of high-speed train surface pressure measured signals

HEHong-yang,CHENChun-jun,MIAOXiao-lang,HEFa-sheng(School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Key words:high-speed train; surface pressure; vibration interference; IEEMD

随着列车的运行速度不断提高，空气动力效应加剧[1-2]。列车在会车压力波及隧道压力波气动载荷作用下，产生巨大的瞬态压力冲击，将会引起列车结构振动及变形[3]；同时，车外压力波通过车窗、门缝隙、焊接缝隙及换气系统进入车内，引起车内压力变化，从而影响乘客的气压舒适性[4]。由此，准确测试列车表面压力至关重要，微型压阻式绝压传感器体积小、重量轻、分辨能力高等优点，被广泛应用于列车表面压力测试[5]。但高速列车实际线路运行时，列车受轨道不平顺和气动载荷等激扰，列车受到多自由度振动，贴在列车表面的压力传感器也受到车体振动冲击，从而引起压力传感器内部结构变化，给测试带来的干扰压力称为振动干扰；同时，车体振动也会引起表面压力变化(称为振动压力)，与振动干扰混杂在一起，其频率重叠，导致难于准确提取列车表面压力。

针对上述问题，本文提出一种改进的集合经验模态分解方法(Improved Ensemble Empirical Mode Decomposition，IEEMD)，对模型车在单自由度方向振动激励下的车体表面压力信号进行IEEMD分解，并以相关系数为依据，提取出振动引起的压力；运用CFD软件仿真计算相同激励下模型车同一测点的振动压力，分离出振动干扰，并建立振动与干扰压力的回归关系，为准确提取高速列车表面压力提供理论指导。

1表面压力信号分析

1.1传感器输出模型

微型压阻式传感器在硅膜片两边有两个压力腔，一个是和被测压力相连接的高压腔，另一个是真空腔，在硅膜片的特定方向上扩散2个等值的半导体电阻，并与其他2个等值的半导体电阻连成惠斯登电桥形式，以作为力-电变换的敏感元件[6]。在实际测试过程中，传感器受到气压、振动加速度和周围环境干扰等影响，其膜片受到外界压力作用时，电桥失去平衡，对电桥加激励电源，便可得到与被测压力成比例的输出电压，通过转化得到与之对应的输出压力，其传感器测试压力为：

P(t)=P0(t)+Pa(t)+na(t)+n(t)

(1)

式中，P(t)为传感器输出压力；P0(t)为平均压力；n(t)为周围环境干扰；Pa(t)+na(t)为振动引起的压力，Pa(t)为振动带来的有效压力(称为振动压力)，na(t)为振动带来的传感器干扰(称为振动干扰)。

由式(1)可知，列车线路运行时，传感器输出压力信号含有周围环境干扰，下面提出一种改进的EEMD方法进行预处理，消除周围环境带来的干扰，从而提取出式(1)右边的中间两项，即振动引起的压力。

1.2改进的EEMD方法

经验模式分解(EMD)是Huang[7]首先提出的一种新型的时域分析方法，将复杂信号自适应地分解为有限IMF分量，反应信号内部的特征。但研究表明EMD对非平稳信号进行分析时，存在两大问题：①端点效应；②模态混叠。

EMD对非平稳信号分析时，在数据的两端会产生发散现象，并且这种发散现象会逐渐向内“污染”整个数据序列而使所得的分解结果严重失真，称之为端点效应[8-12]。针对端点效应问题，国内外学者做了大量的研究，总结为波形延拓法、数据预测延拓法、极值延拓法三类方法[9]。本文采用最小二乘支持向量机(LS-SVM)方法对端点进行预测延拓：将最小二乘线性系统作为损失函数，将不等式约束条件转化为等式约束；针对非线性样本数据，首先用非线性映射ψ(·)把样本从原空间映射到特征空间φ(xi)，定义核函数为：

K(xi,yi)=φ(xi)·φ(yi)

(2)

常用的核函数有：多项式核函数、径向基核函数和Sigmoid核函数；同时将优化问题转化为求解线性方程，最后用最小二乘法求出a和b，得到非线性预测模型如式(3)所示：

(3)

LS-SVM良好的回归预测性能对信号极值点幅值进行预测延拓，对给定的信号在端点处延拓有限个数据点，从而得到延拓序列。LS-SVM能很好地抑制端点效应，但仍有待提高，其端点效应仍不确定，可能在两端造成发散现象，继续向内“污染”。目前已经提出了一些数据延拓和窗函数相结合的方法[10-11]，下面将LS-SVM和余弦窗函数结合，在保留波形延拓方法优势的基础上，通过加余弦窗函数，使端点为零，信号的包络线变得比较平滑，样条函数可以更好的拟合包络线，上下包络线收敛于端点，更有效地消除端点效应。其表达式如下[12]：

(4)

式中，L为信号延拓后的长度；A为延拓信号的较长延拓长度，其余弦窗函数的形状见图1。然后对信号进行EMD分解，将分解后的得出的IMF的延拓部分去掉，从而达到很好地抑制EMD端点效应。

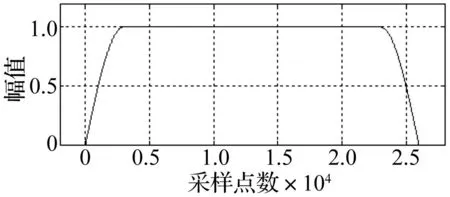
图1　余弦窗函数形状 Fig.1 The shape of cosine window

同时，为了抑制模态混叠，Wu等[13]提出了一种集合经验模式分解方法，该方法将噪声辅助分析应用于经验模式分解中以促进抗混分解，有效抑制了模式混叠现象。文献[14]在EEMD基础上提出了AEEMD，同时应用在转子油膜涡动的故障监测诊断中，提取出转子油膜涡动的故障特征，取得了很好的效果。使用EEMD进行经验模态分解时，需要设置两个参数，即加入原信号的噪声幅值k和执行EMD的总次数M，加入噪声对分解结果e的影响与k、M的关系式为：

(5)

式中k越小M越大则e越小，但当k过小时，不足以引起信号局部极值点的变化，M过大将增加耗时，不利于实时分析。因此本文根据文献[14]提出的EEMD加入白噪声的自适应准则，确定k和M值。

1.3仿真实例分析

为了验证1.2节所述的改进方法的有效性，设计一个仿真信号s，信号s由频率为10Hz和频率为20Hz的正弦信号，以及标准差为0.2的白噪声组成，仿真原始信号s见图2。具体步骤如下：

步骤1利用LS-SVM对端点进行预测延拓。对原始仿真信号两端分别延拓20个数据点，取参数gam=20，sig2=0.5，RBF作为核函数；

步骤2余弦加窗处理。将延拓信号s(t)与余弦窗函数进行内积运算；

步骤3EEMD分解。对加窗后的仿真信号进行EEMD分解，根据自适应准则得到k=0.02,M=200，再将各IMF分量两端去掉相应的延拓部分。

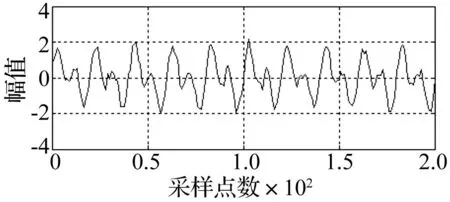
图2　仿真信号 Fig.2 Simulation signal

对原始信号s进行EMD分解和IEEMD分解。由图3可知，EMD分解的结果中IMF3～IMF5分量中在端点处均出现发散现象；同时各IMF分量均存在严重的模态混叠现象。而改进的EEMD分解可以很好抑制端点效应和模态混叠现象。

图3　EMD和改进的EEMD分解的各IMF分量 Fig.3 IMF component of EMD and improved EEMD

2模型车试验及仿真分析

高速列车实际线路运行时，列车受轨道不平顺和会车气动载荷等激扰，车体产生多自由度振动，其贴在车体表面的传感器输出干扰也比较复杂。因此，本文通过模型车试验，在单自由度方向振动激励下进行分析。

2.1模型车试验

由于实际线路较复杂，通过模型车试验装置，将模型车放置在实验室台架上，同时将微型压阻式传感器贴在模型车车内表面，编号为①，在模型车的底板贴上三向振动加速度传感器，编号为②；传感器均用·(小黑点)表示。模型车示意图见图4，系统采样频率为2K。

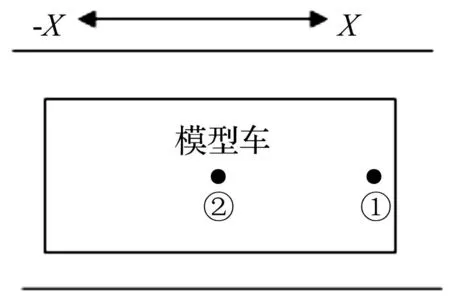
图4　模型车示意图(①为气压测点，②为振动加速度测点) Fig.4 Diagram of model-train(①pressure measuring point, ②vibration acceleration measuring point)

对模型车给以沿水平方向(x方向)的单自由度振动激励，分析传感器测点信号的变化。图5(a)为减去均值后的传感器输出压力时域图，由振动压力Pa(t)、振动干扰na(t)以及电磁干扰n(t)3部分组成，即式(1)中的后3项；传感器输出压力总是波动的，其幅值在±20Pa左右。对应的振动激励信号见图5(b)，在0～1.5s模型车静止，其加速度值为0，在1.5～11.5s模型车给以单自由度振动激励，其加速度幅值为±2g左右。

图5　测试信号时域图 Fig.5 Time-domain chart of test signal

2.2CFD计算模型车表面压力

由1.1节可知，振动引起的压力包括振动压力和振动干扰，其频段重叠，难于分离。下面利用流体力学计算软件CFD仿真模型车在相同激励下测点处的压力，即振动压力，作为测点压力的理论标定值。采用不可压缩流三维瞬态的雷诺时均Navier-Stokes方程和工程中常用的标准κ-ε方程的湍流模型获得模型车车内测点的压力。

图6　模型车网格划分(①为固定网格，②为动网格) Fig 6 Model car mesh(①fixed mesh, ②dynamic mesh)

模型车运动物理模型见图6，外流场区域长3000mm，宽1400mm，高为1000mm。模型车运动模型流场区域分为动网格部分和固定部分，其中①为固定网格，②为动网格，动网格部分是包含模型车周围的网格区域。动网格部分以模型车运行速度进行滑移，滑移速度通过图5(b)所示加速度积分得到；同时，通过建立交界面进行动网格和固定网格之间的数据传递。本文模型采用全六面体网格，对模型车的内外壁面的边界层设为5层进行网格加密，第一层网格厚度为1mm，模型网格总数约为180万。边界条件的设定如下：对于模型车壁面、流场区域底面采用壁面边界条件其他外场外界都采用压力出口边界条件，给定标准大气压101.325kPa。

由于利用软件仿真可有效地避免传感器在测试过程中带来的干扰，在相同激励下，通过CFD软件仿真计算得到振动压力Pa(t)，其幅值在±3Pa左右。加载的振动加速度激励(用虚线表示)和振动压力Pa(t)(用实线表示)的时域波形见图7，可知振动压力与振动加速度有相同的变化趋势。

图7　CFD仿真压力信号 Fig.7 The chart of pressure signal by CFD simulation

3振动干扰提取与分析

3.1振动引起的压力

针对见图5(a)的压力信号，取1.5～11.5s压力数据进行改进的EEMD方法分解，其IMF分量自适应地从测试压力信号中分解出来，分为14层和余项，其中IMF9～IMF14(限于篇幅，这里只列出部分IMF分量)分量见图8。每个IMF分量都有相应的主频，但各个频段的幅值具有很大差异，说明振动引起的压力在全频段不是均匀分布的，而是集中分布在若干个频段中。

图8　测试压力信号的IEEMD分解结果 Fig.8 The decomposition result of test pressure signal

由图5可知，在单自由度振动激励下，模型车的振动加速度和车体表面压力表现为一定的周期性。根据自相关函数的性质，周期性信号的自相关函数是周期的，自相关函数凸显原函数的周期性；干扰信号的自相关函数在0时取得最大，并且快速衰减至零[15]。为了更精确地得到振动引起的压力，首先计算出各IMF分量的自相关函数RIMF1,…RIMF K和原始信号的自相关函数Rx，其表达式为：

(6)

然后将自相关函数作归一化处理，求得原函数自相关函数Rx与IMF分量自相关函数RIMF1,…RIMF K之间的相关系数，相关系数的计算公式为：

(7)

式中，N为数据的长度；一般情况下，设置阀值ρ(j)为0.5，大于阀值的IMF分量视为有效分量，与原始信号的相关性好，给以保留。

根据表1可知，IMF10和IMF11的相关系数均大于0.5，认为是有效的IMF分量，进行重构得到振动引起的压力信号。对传感器输出信号消除电磁干扰n(t)，得到振动引起的压力信号，由振动压力Pa(t)和振动干扰na(t)两部分组成，与振动加速度有相同的变化趋势，其幅值为±8Pa左右，时域图见图9(a)。同时对振动加速度和振动引起的压力信号做频谱分析，由频域图见图9(b)可知，其频率成分相同，这是因为振动引起的压力信号是由振动加速度引起的，同时也证明了上述提取方法的正确性。图中振动加速度用虚线表示，振动引起的压力用实线表示。

图9　振动引起的压力信号 Fig.9 The chart of pressure signal from vibration

IMFj1234567ρ(j)0.06880.04130.04170.03270.26100.25490.0314IMFj891011121314ρ(j)0.03620.08040.95240.72580.06530.08650.0951

3.2振动干扰特性分析

上述运用改进的EEMD方法分解出振动引起的压力，由振动压力Pa(t)和振动干扰na(t)两部分组成；而通过CFD仿真计算得到相同激励下的振动压力Pa(t)，即可分离出振动干扰na(t)。下面应用回归分析的方法分别确定振动加速度与振动压力、振动干扰之间的定量关系式。

由上述可知振动加速度与振动压力和振动干扰有相同的变化趋势，故采用线性回归分析的方法研究它们之间的定量关系式[16]，其表达式如(8)式所示：

P=A×a

(8)

式中：a为振动加速度，单位为g；P为振动压力或振动干扰，单位为Pa；A为回归系数。

通过CFD计算得到的振动压力与振动加速度线性回归关系见图7，可知其回归系数A1=1.5；分离出的振动干扰的幅值大致在±5Pa左右，与振动加速度有相同的变化趋势，利用线性回归分析方法可知回归系数A2=2.5，从而得到线性回归分析参数见表2。列车在实际线路运行时，应用上述建立的回归关系，通过测试车体振动加速度，可得到车体振动引起的气压干扰。

表2　回归参数

4结论

(1)针对经验模态分解过程中存在端点效应和模态混叠现象，提出了一种改进的EEMD方法，对仿真信号和模型车表面压力信号的降噪结果表明了该降噪方法的可行性和有效性；

(2)对高速列车表面压力测试信号组成以及传感器干扰进行了理论分析。通过搭建单自由度激励下的模型车振动试验平台，并结合流体计算软件对车内流场进行模拟，分离出振动引起的传感器干扰压力。为列车表面压力测试信号的分离提供了一种新的手段；

(3)本文得到振动加速度和振动干扰的线性回归关系为：na(t)=2.5a。利用这一结论，在高速列车空气动力学测试时，可根据振动加速度运用上述关系式计算振动干扰，从而准确地提取出列车表面压力。

参考文献

[1]田红旗. 列车空气动力学[M]. 北京:中国铁道出版社, 2007.

[2]Raghu S, Kim H D, Setoguchi T. Aerodynamics of high-speed railway train [J]. Progress in Aerospace Science, 2002, 38: 469-514.

[3]田红旗，姚松，姚曙光. 列车交会压力波对车体和侧窗的影响[J]. 中国铁道科学,2000,21(4):8-14.

TIAN Hong-qi, YAO Song, YAO Shu-guang. Influence of the air pressure pulse on car-body and side-windows of two meeting trains [J].China Railway Science, 2000,21(4): 8-14.

[4]田红旗，梁习锋. 准高速列车交会空气压力波试验研究[J].铁道学报,1998,20(04):37-39.

TIAN Hong-qi, TIANG Xi-feng. Test research on crossing air pressure pulse of quasi-high-speed train[J].Journal of the China Railway Society,1998,20(02): 37-39.

[5]蒋小燕，徐大诚，杨成,等. 硅压阻式压力传感器非线性误差校正方法[J]. 传感器与微系统,2006,25(1):76-77.

JIANG Xiao-yan, XU Da-cheng, YANG Cheng, et al. Nonlinear errors correcting method of piezoresistive pressure transducer[J].Transducer and Microsystem Technology,2006,25(1):76-77.

[6]张栋，李永红. 机载压阻式压力传感器设计与加工[J].仪表技术,2007,6:62-64.

ZHANG Dong, LI Yong-hong. Study on pressure sensor based on MEM S processing technology[J].Instrumentation Technology, 2007,6:62-64.

[7]Huang N E. The empirical model decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proc. R. Soc. Lond. A, 1998,454:903-995.

[8] 陈双喜，林建辉，陈建政. 基于改进的EMD方法提取车辆-轨道垂向耦合系统动态特性[J]. 振动与冲击,2011,30(8):213-216.

CHEN Shuang-xi,LIN Jian-hui, CHEN Jian-zheng. Dynamic characteristics extraction of vehicle-track vertically coupling system based on improved EMD [J]. Journal of Vibration and Shock, 2011, 30(8): 213-216.

[9]郭明威，倪世红，朱家海,等. 振动信号中HHT/EMD端点延拓方法研究[J]. 振动与冲击,2012,31(8):62-65

GUO Ming-wei, NI Shi-hong, ZHU Jia-hai,et al. HHT/EMD end extension method in vibration signal analysis [J].Journal of Vibration and Shock, 2012, 31(8): 62-65.

[10]李敏，程珩，张斌. EMD端点效应处理方法研究[J]. 太原理工大学学报,2009,40(6):579-581.

LIN Min, CHENG Hang, ZHANG Bin. Study on method dealing with the end effect of EMD [J]. Journal of Taiyuan University of Technology, 2009,40(6):576-581.

[11]旷欢，王如龙，张锦,等. 基于SVM的EMD端点效应抑制方法研究[J]. 计算机工程与应用,2014.

KUANG Huan, WANG Ru-long, ZHANG Jin, et al.Study on suppression of EMD end effect based on SVM [J].Computer Engineering and Application, 2014.

[12]时培明，丁雪娟，李庚,等. 一种EMD改进方法及其在旋转机械故障诊断中的应用[J]. 振动与冲击. 2013,32(4):186-188.

SHI Pei-ming,DING Xue-juan, LI Geng, et al An improved method of EMD and its application in rotating machinery fault diagnosis [J].Journal of vibration and shock, 2013, 32(4): 186-188.

[13]Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009,1(1):1-41.

[14]蔡艳平，李艾华，徐斌,等. 集成经验模态分解中加入白噪声的自适应准则[J]. 振动、测试与诊断,2011,31(6):709-713.

CAI Yan-ping, LI Ai-hua, XU Bin, et al. Adaptive guideline of ensemble empirical mode decomposition with gauss white noise[J].Journal of Vibration, Measurement & Diagnosis, 2011,31(6):709-713.

[15]陈仁祥，汤宝平，吕中亮. 基于相关系数的EEMD转子振动信号降噪方法[J]. 振动、测试与诊断,2012,32(4):542-544.

CHENG Ren-xiang, TANG Bao-ping, LÜ Zhong-liang Ensemble empirical mode decomposition de-noising method based on correlation coefficients for vibration signal of rotor system [J].Journal of Vibration, Measurement & Diagnosis, 2012,32(4):542:544.

[16]李再帏，连松良，刘晓舟. HHT在车辆-轨道系统垂向振动时频分析中的应用[J]. 振动、测试与诊断,2013,35(5):801-803.

LI Zai-wei,LIAN Song-liang, LIU Xiao-zhou Time-frequency analysis of vehicle-track vertically coupling system based on Hilbert-Huang Transform [J].Journal of Vibration, Measurement & Diagnosis, 2013,35(5):801-803.

第一作者王欢欢男，博士生，1986年生

通信作者金先龙男，教授，博士生导师，1961年生

邮箱：jxlong@sjtu.edu.cn

第一作者李正良男，博士，教授，1963年生

通信作者刘欣鹏男，博士，1987年生