基于空气流体动力学的高速列车制动盘散热性能模拟

王玉光　周茜　乔青峰　马利军

摘要：基于CFD法分析高速列车制动盘的散热情况，得到制动盘各个区域的平均对流换热系数.在此散热条件下，用顺序耦合法模拟制动盘的温度场，实现复杂六边形热载荷的加载，并将二次制动温度场的模拟结果与试验数据进行对比分析.结果表明：模拟结果与试验数据在冷却阶段吻合度较高，且在制动阶段中最高温度值误差不超过5%.

关键词：高速列车； 盘式制动； 散热； 热对流； 温度分布

中图分类号： U260.351 文献标志码：B

Abstract：The heat dissipation of the brake disk of a highspeed train is simulated by CFD method， and the average convective heat transfer coefficients of each part of the brake disk are calculated. Under the heat dissipation condition， the temperature field of the brake disk is simulated by sequential coupling method， the thermal load of complex hexagon shape is loaded， and the simulation results of the second braking temperature field is compared with the test results. The results show that， the simulation results are consistent with the test data in the cooling stage， and the maximum error of the temperature is less than 5% during the braking stage.

Key words：highspeed train； disk brake； heat dissipation； heat convection； temperature distribution

0 引 言

在高速列车制动过程中，制动盘与闸片摩擦接触产生大量的热，多次制动会引起摩擦副材料热疲劳裂纹直至破坏.由于当前仍无可靠的方法有效测定或预测制动能量和热疲劳裂纹发展演变过程，所以通过数值仿真分析高速制动盘的散热性能对于制动盘材料的选取和结构设计有重要的指导意义.[1]

空气对流传热是制动盘散热最主要的能量交换方式.以往研究中，对流传热系数的计算多采用经验公式.[24]该方法对于一些几何规则的模型适用性好、计算简便，但是对于复杂结构，如动车组使用的轮装制动盘的散热筋，估测经验公式中散热面特征长度存在较大困难.为此，一些学者采用计算流体力学（Computational Fluid Dynamics，CFD）方法分析复杂结构的散热特性.BELHOCINE等[5]以1/4制动盘为研究对象，模拟静止空气中旋转制动盘各个区域的平均对流传热系数，JIANG等[6]模拟列车轴装制动盘在实际行进过程中的对流传热特性.参考以上研究，论文基于CFD技术仿真高速动车组轮装制动盘的流体场，获得不同运行速度下制动盘不同表面上的平均对流传热系数.

利用有限元分析制动盘的温度场时，有顺序耦合法和直接耦合法之分.直接耦合法考虑应力与温度的相互作用，模拟结果对高温作用下制动盘与闸片之间的真实接触面积敏感，极容易出现数值收敛性困难的问题[7]；顺序耦合法将摩擦接触简化为加载摩擦热量，因此容易收敛[8].考虑到多边形热载荷作用范围不易确定，在讨论多边形闸片结构对应的制动盘温度场时，以直接耦合法为主.[27]基于几何原理，用顺序耦合法模拟六边形闸块对应的制动盘温度场，并将二次制动的温度场结果与实测值对比，表明计算结果可靠.

1 有限元模型

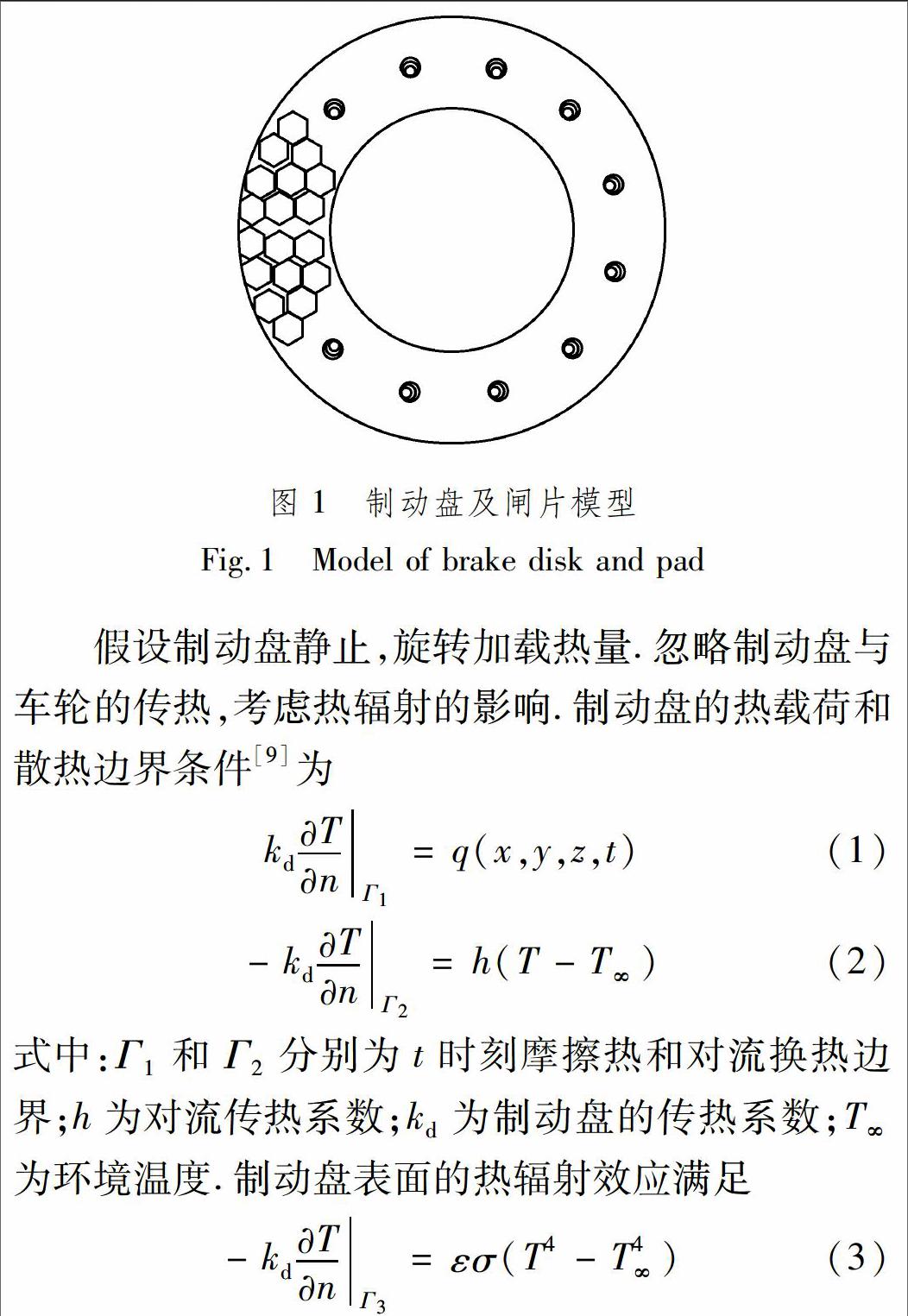
动车组轮装制动盘和六边形闸块模型见图1.以单个制动盘为研究对象，将制动盘与闸片之间摩擦产生的热量加载在制动盘上.

空气通风速度为列车速度的1/2，忽略闸片对流场的影响，取轮子、制动盘和轴的表面作为流场的壁面.通风状态下强迫对流是制动盘散热的主要途径，因此可忽略自然对流影响.研究表明：与经验公式和经典kω模型相比，SST kω模型的计算复杂度和计算精度有明显优势，因此作为计算流体力学模型.

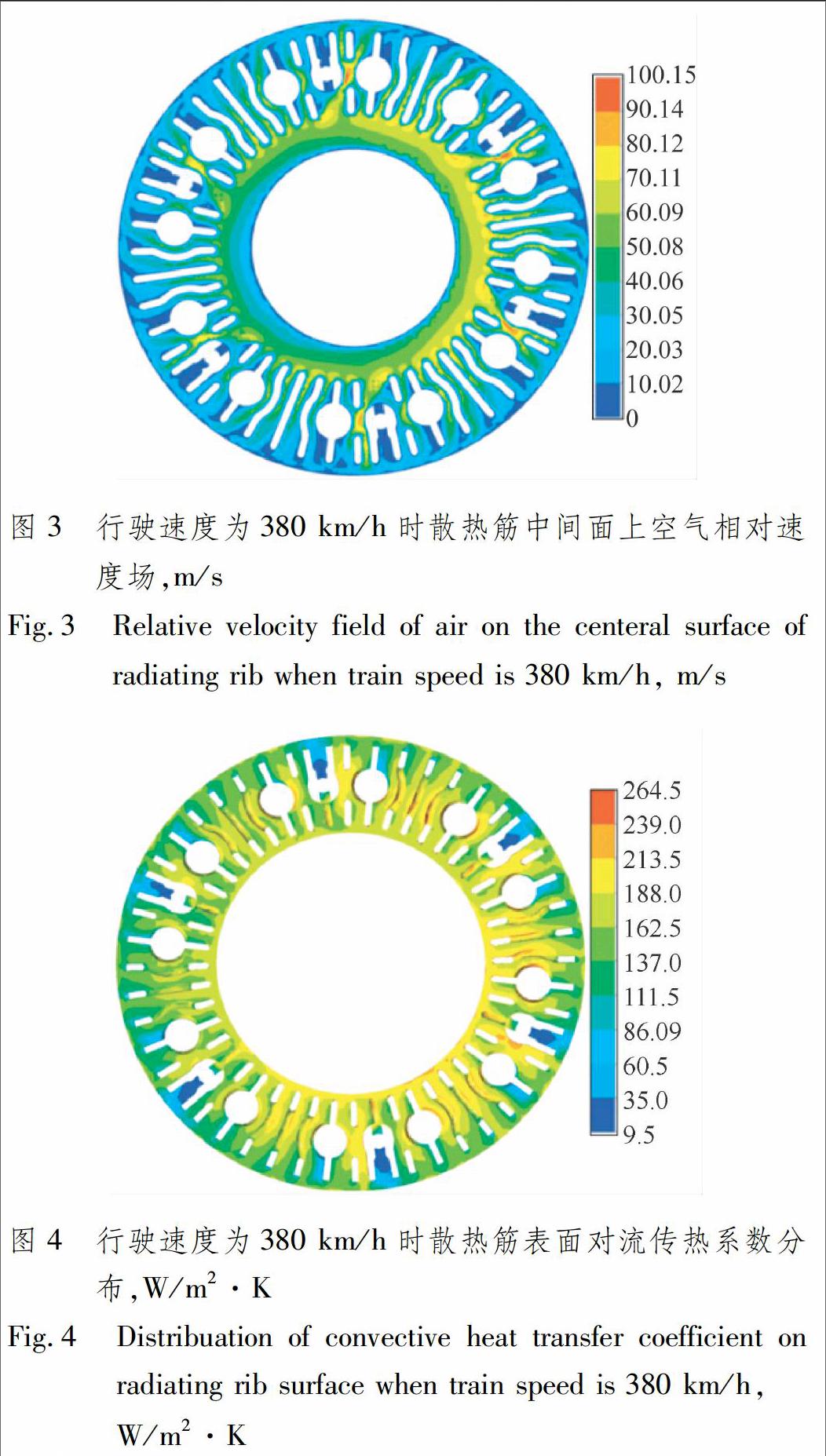
用CFD模拟行驶过程中制动盘周围的流场，得到制动盘散热筋附近的空气流动传热情况.列车行驶速度为380 km/h时制动盘的散热筋中间面上空气相对速度场和散热筋表面对流传热系数分布云图分别见图3和4.受列车通风状态和制动盘转动的共同影响，当旋转引起的空气流动方向与通风方向一致时，对流传热系数增大，反之减小.

3 二次制动温度场计算结果和分析

列车在二次制动过程中的对流传热系数时间曲线见图6.由此可知：制动盘表面传热系数并不呈现单调递增或递减变化趋势，而是先急剧下降再迅速上升至峰值约360 W/（m2·K），最后再急剧下降的变化形式.据此认为，制动盘面某区域的温度场并非维持固定不变，而是在制动过程中呈现交替变化，这也是热疲劳裂纹产生的重要原因之一.

根据上述传热系数变化分析温度场变化.列车制动初速度为380 km/h，二次制动时间总长622 s，制动盘制动半径约为280 mm.对二次制动工况下制动盘的温度场进行有限元分析，在制动盘摩擦面某径向上选取一组节点，得到节点温度随时间变化曲线，见图7.由图7可知：在制动阶段，制动盘摩擦面上的最高温度分布在距离旋转中心约314 mm附近，该组节点的最高温度为722.5 ℃；冷却阶段该组节点温度趋于一致，温度都在125 ℃左右.进行制动台架试验，制动盘面上布置若干热电偶，在制动装置下方鼓风，并控制风速为旋转线速度的1/2，以模拟真实行驶状态.提取二次制动过程中每个时间步对应的热电偶最高温度值，与有限元模拟的最高温度值比较，见图8.图8显示：在第一次制动过程中，制动盘最高温度模拟结果为687.7 ℃，比试验结果高8 ℃，误差率约1.1%；第二次制动结果为742 ℃，比试验数据高35 ℃，误差率约为5.0%.与图7相比，在2次制动阶段，摩擦面上提取的最高温度值比固定节点的最高温度约高20 ℃，冷却阶段误差很小.由此来看，图8中误差产生的原因除与顺序耦合方法有关外，可能与制动盘面上个别节点处出现瞬时高温有关.

从图8还可以看出：在冷却阶段，模拟的曲线与试验数据吻合度较好，表明制动盘的散热情况得到有效模拟.

4 结 论

通过分析高速列车制动盘在行驶过程中的散热情况，以及二次制动过程中的温度场变化，得出如下结论：1）在制动阶段，制动盘最高温度出现在制动半径附近，2次最高温度误差都不超过5%，证明用顺序耦合法模拟六边形热载荷满足工程需要；2）在冷却阶段，制动盘各部分温度趋于一致，与试验曲线吻合度较好，表明CFD可有效模拟制动盘散热情况.

参考文献：

[1]方明刚， 杜利清， 郭立宾， 等. 制动盘热机械耦合仿真系统的开发[J]. 铁道机车车辆， 2014， 34（6）： 6973.

FANG Minggang， Du Liqing， GUO Libin， et al. Development of thermal mechanical coupling simulation system for brake disc[J]. Railway Locomotive & Car， 2014， 34（6）： 6973.

[2]王艺， 陈辉， 李明. 高速列车制动盘制动过程数值模拟[J]. 机械， 2008， 35（3）： 1517.

WANG Yi， CHEN Hui， LI Ming. Numerical simulation of brake discs for highspeed trains[J]. Machinery， 2008， 35（3）： 1517.

[3]张涛， 王梦昕， 丁亚琦， 等. 动车制动盘温度场和热应力场的耦合分析[J]. 兰州交通大学学报， 2011， 30（6）： 119122.

ZHANG Tao， WANG Mengxin， DING Yaqi， et al. Coupling analysis of temperature and stress fields for brake disc on power car[J]. Journal of Lanzhou Jiaotong University， 2011， 30（6）： 119122.

[4]张乐乐， 杨强， 谭南林， 等. 基于摩擦功率法的列车制动盘瞬态温度场分析[J]. 中国铁道科学， 2010， 31（1）： 99104.

ZHANG Lele， YANG Qiang， TAN Nanlin， et al. Analysis of the transient temperature field of train brake discs based on friction power method[J]. China Railway Science， 2010，31（1）： 99104.

[5]BELHOCINE A， BOUCHETARA M. Thermal analysis of a solid brake disc[J]. Applied Thermal Engineering， 2012， 32： 5967.

[6]JIANG L， JIANG Y L， YU L， et al. Thermal analysis for brake disks of SiC/6061 Al alloy cocontinuous composite for CRH 3 during emergency braking considering airflow cooling[J]. Transaction of Nonferrours Metals Society China， 2012， 22（11）： 27832791.

[7]农万华， 高飞， 符蓉， 等. 摩擦块形状对制动盘摩擦温度及热应力分布的影响[J]. 润滑与密封， 2012， 37（8）： 5256.

NONG Wanhua， GAO Fei， FU Rong， et al. Influence of brake pad shape on friction temperature and thermal stress of brake disc[J]. Lubrication Engineering， 2012， 37（8）： 5256.

[8]ADAMOWICZ A， GRZES P. Analysis of disc brake temperature distribution during single braking under nonaxisymmetric load[J]. Applied Thermal Engineering， 2011， 31（67）： 10031012.

[9]吴圣川. 复杂件等离子熔积成形过程有限元及无网格法模拟[D]. 武汉： 华中科技大学， 2009.

[10]GHADIMI B， SAJEDI R， KOWSARY F. 3D investigation of thermal stresses in a locomotive ventilated brake disc based on a conjugate thermofluid coupling boundary conditions[J]. Intnational Communications Heat and Mass Transfer， 2013， 49： 104109.

[11]金星， 魏秀琴. 高速列车制动盘表面对流换热系数的研究进展[J]. 企业技术开发， 2014， 33（28）： 3739.

JIN Xing， WEI Xiuqin. The research progressof convective heat transfer coefficient on the surface of the highspeed train brake disc[J]. Technological Development Enterprise， 2014， 33（28）： 3739.

（编辑 武晓英）