低质量比圆形四立柱涡激运动特性研究

低质量比圆形四立柱涡激运动特性研究

刘为民，谷家扬，陶延武，渠基顺，吴介

(江苏科技大学船舶与海洋工程学院,江苏镇江212003)

摘要：采用有限体积法对圆形四立柱涡激运动进行数值模拟。圆形四立柱涡激运动系统简化为两自由度的质量-弹簧-阻尼模型，引入雷诺平均应力模型求解不可压缩粘性Navier-Stokes方程,并结合SST k-w湍流模型对低质量比弹性支撑的圆形四立柱涡激运动进行模拟。将四阶Runge-Kutta代码嵌入用户自定义函数UDF(User Defined Function)中求解四立柱的动力响应，采用动网格技术来实现立柱和流场之间的耦合。研究发现，圆形四立柱涡激运动流向和横向振幅随着折合速度的增大而先增大后减小，并出现幅值跳跃现象，跳跃点在折合速度9.0处。横向振幅最大值出现在折合速度为8.0时，大小为1.99D，远大于流向振幅最大值0.26D。圆形四立柱流向运动平衡位置随折合速度增大并非一直增大，在折合速度9.0时突然下降随后增大。圆形四立柱涡激运动出现了明显的频率锁定现象，锁定区间为5.0～8.0。当系统走过锁定系统后，流向幅值和流向幅值迅速减小。最后对不同折合速度下圆形四立柱运动轨迹和尾涡脱落模式进行讨论分析。

关键词：圆形四立柱；涡激运动；频率锁定；动网格

中图分类号:P75

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.028

Abstract:Here, the finite volume method was used to simulate vortex-induced motion of four circular columns. The vortex-induced motion system of four circular columns was simplified into a spring-mass-damping model. Reynolds-averaged Navier-Stokes solver was combined with SST (shear-stress transport) k-ω turbulence model for solving Navier-Stokes equation to simulate the vortex-induced motion of four circular columns with a low mass ratio. Fourth order Runge-Kutta method was manually written into the user defined functions to get the dynamic response of four circular columns, and then the dynamic mesh technology was adopted to realize the coupled fluid-structure interaction. It was shown that the amplitudes of the four circular columns firstly increase and then decrease with increase in the reduced velocity, ’jump’ phenomenon is observed in the amplitude curve at the reduced velocity of 9.0; the transverse maximum amplitude appears at the reduced velocity of 8.0, its value is 1.99D, much larger than the stream-wise maximum amplitude 0.26D; the in-line balance positions of four columns do not always increase with increase in the reduced velocity, it suddenly decreases at the reduced velocity of 9.0 and then increase; the frequency lock-in phenomenon occurs in four circular columns vortex-induced motion, the lock-in region is in the range of the reduced velocity of 5.0～8.0; when the vortex-induced motion system passes the lock-in region, the stream-wise amplitude and the transverse one suddenly decrease; finally, the trajectory and tail vortex shedding pattern of four circular columns at different velocities are discussed.

Vortex-induced motion characteristics of four circular columns with a low mass ratio

LIUWei-min,GUJia-yang,TAOYan-wu,QUJi-shun,WUJie(School of Naval Architecture and Marine Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China)

Key words:four circular columns; vortex-induced motion; frequency lock in; dynamic mesh

海洋结构物涡激运动(Vortex-Induced Motion, VIM)这一热点问题越来越受到目前深海工程技术人员和研究人员的关注，它是典型钝体绕流中升力和拖曳力所导致的直接后果。由于流体具有一定的粘性, 一定来流下的流体流经柱状海洋结构物时会在两侧产生交替的漩涡，当结构物后面的漩涡释放时会产生横向和流向的脉动力。若海洋结构物的支撑方式是弹性支撑，横向和流向的脉动压力会促使柱体进行周期性的往复运动。流向的脉动力使结构物产生流向的纵荡周期性往复运动，横向的脉动力使结构物产生横荡周期往复运动。在海洋工程领域中，不管海洋石油开采采用何种的平台结构形式，它们的结构都有着一个很大的特点，即由多柱体构成。例如Spar平台是单柱体结构，柱体的形状一般为圆柱形。半潜式平台一般有三个或四个立柱，立柱的截面形式一般以圆形和方形为主，并以一定的形式排列。张力腿平台的立柱形式和半潜式平台的立柱形式非常类似，一般立柱的截面也是以圆形和方形为主，其中以四立柱阵列排布的比较多。对于海洋平台中的各种柱体结构，不能忽视的一个问题就是涡激运动。涡激运动的存在会相应的增加锚链和立管等结构物的疲劳破坏，进而缩短海洋结构物总体疲劳寿命，增加结构物上的总阻尼。若忽略涡激运动这一现象，海洋结构物疲劳分析和锚链最大张力的计算结果都将偏小，致使设计者对锚链和立管的相关尺度参数估算偏低。

由于平台多立柱之间的流动分离和剪切层干扰效应的复杂性，结构所受到的流体力与相关频率特性具有强烈的非线性特性，因此钝体的存在导致这个流场结构与受力特性变得更加复杂并且与单体结构有明显的区别。目前，多个柱体之间的相互作用成为了国内外学者研究的热点。柱体排列方式主要有串列、并列和交错排列，不同排列方式对涡激运动的影响可参考相关文献[1-9]。万德成[10]采用多重网格虚拟边界有限元法对一个大圆柱捆绑四个小圆柱在粘性流场中的受迫运动和自激运动进行数值模拟，着重分析了多圆柱在受迫运动和自激运动的泻涡结构特征与多圆柱运动之间的关系。徐枫等[11]采用有限体积法对低雷诺数下正方形排列等直径的两自由度涡激振动进行了数值模拟。重点研究了在不同的间距比下圆柱的频 率 特 性、尾流漩涡脱落模式。结果发现上游圆柱的横向和流向最大幅值分别为0.82D和0.66D，而下游的流向和横向幅值均为0.75D。徐枫等[12]通过有限体积法求解二维不可压缩N-S方程，对正三角形排列的等直径圆柱进行了涡激振动的数值模拟。重点研究了在间距比1.5～6.0的范围内，圆柱的气动力响应和相关的频率特性、尾流流动模式的变化规律，结果发现在间距比3.5～4.0范围内气动干扰最为强烈，此时各圆柱体的横向幅值均能达到0.9D，而下游圆柱的流向振幅更大，达到1.1D。徐枫等人的研究流场的介质是风，对海洋工程结构物涡激运动的研究有一定的参考价值。Ming等[13]对两自由度阵列圆柱体的涡激振动进行了数值模拟，通过有限体积法来求解二维不可压缩N-S方程和SSTk-w紊流方程。折合速度从1到20每间隔1，对0°、15°、30°和45°四个不同的流向角下的涡激振动进行了比较分析。

本文以某海洋平台四圆形立柱为研究对象，研究由圆形四立柱引起的涡激运动。模型简化为二维立柱截面。二维平台立柱截面模型简单，耗时时间少，可以方便快捷的研究无浮箱时立柱后方的尾流特性，包括立柱的涡激运动载荷，涡激运动响应，以及尾流场中尾流特性等。

1数值计算方法

1.1计算流体力学控制方程

不可压缩粘性流体的控制方程为质量和动量守恒方程，

(1)

(2)

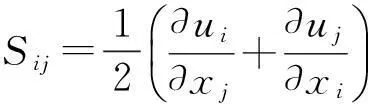
1.2无因次动力学控制方程

(3)

(4)

1.3计算模型

本文的研究对象选取为某深吃水四立柱平台。此平台由4个立柱和4个浮箱组成，主要性能参数见表1。四立柱平台发生涡激运动时，水下的立柱是其有效激励部分，因此本文重点关注立柱所诱导产生的涡激运动，忽略浮箱对尾流的影响。

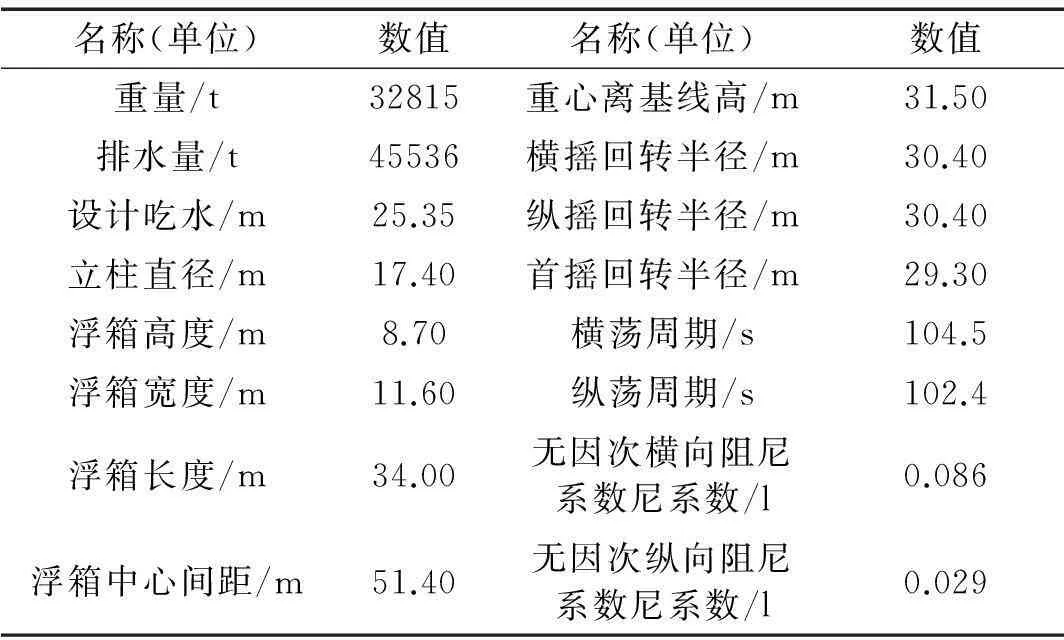
表1　四立柱平台主要性能参数

本文运用Fluent前处理软件Gambit按照1∶40的比例建立二维四立柱模型。在整个模型中笔者采用了三角、四边形混合网格模型，近场区域使用致密的四边形网格，这样很好的捕捉到柱体的尾流特性，远场处采用相对稀疏的三角形网格。整个计算流域为50D×30D，其中D为圆柱的直径，见图1。坐标原点位于上游两立柱中心点的连线中点处，原点离上游入口为15D，距离下游出口为35D。立柱壁面的贴体网格必须布置在粘性底层内，所以壁面第一层网格满足y+≈1。计算流场域采用Fluent分离求解器进行求解，采用SSTk-ω湍流模型和非稳态一阶隐式进行求解，动量方程的压力速度耦合采用SIMPLEC算法，动量、湍流动能、耗散率项均采用二阶迎风格式以减少数值耗散。左侧采用速度入口边界(Velocity inlet)，右侧为压力出口(Pressure-outlet)，上下边界为自由滑移壁面(Symmetry)，立柱表面为无滑移壁面(Wall)。

3.前奏与尾声的乏味性。这是我们教师缺乏对教材、教法的深入研究。这样的准备活动与结束部分：一是内容枯燥、一般化，不能很好地体现出每个教材类型的特点；二是形式单一化，不能适应不同年段学生的身心特点。因此被视为前奏与尾声的乏味性。

图1　圆形四立柱整个流域网格(a) 和圆形四立柱局部网格(b-c) Fig.1Computational grid of four circular columns (a) and close view of computaional grid (b-c)

本文采用动网格技术来实现立柱和流体之间的耦合作用，在每个时间步内首先求解流体力学控制方程从而得到流体的速度场、压力场以及作用于立柱上的升力和拖曳力，通过UDF获取作用在立柱上的流体力并将它带入结构动力学控制方程，利用自编的四阶Runge-Kutta程序求得圆柱运动响应，然后通过DEFINE_CG_MITION宏函数将圆柱运动响应传递给圆柱并更新流场参数，开始新的循环。本文计算模型的特征值D为0.435m，质量比m*=0.72，固有频率fn=0.061，且流向和横向频率比fnx/fny=1.0，折合速度范围U*=2.0～12.0。

2计算结果与分析

研究柱体涡激运动的特性，其中运动幅值是考察的一个重要数据，既要关注运动幅值的最大值，又要关注幅值的标称值，因此本文采用两种统计方法对振幅进行统计，一种为最大振幅统计法，另一种为标称振幅统计法，具体公式如下：

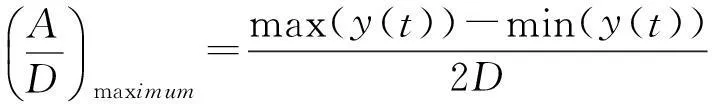
(5)

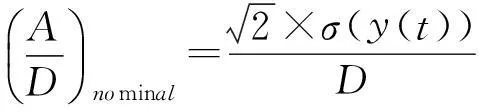
(6)

式中max(y(t))为最大位移min(y(t))为最小位移σ(y(t))为位移标准差。

图2给出了两种统计方法下圆形四立柱涡激运动流向振幅的统计结果。从整体上看，两种统计方法下流向振幅随着折合速度变化的规律类似，出现先增大，再平稳，然后出现幅值跳跃后又趋于平稳的态势。流向振幅在折合速度为7.0时达到最大值0.26D，中间的平稳区间为4.0～7.0，这与圆形四立柱锁定区间有关。从标称振幅统计结果上看，流向振幅仍是在折合速度为7.0时达到最大值，但其大小为0.20D，当折合速度不大于8.0时，振幅随折合速度变化的波动性较强。但是不管是哪种统计结果，当折合速度到9.0时，流向振幅都是陡然下降，随后稳定在一定的数值，且此时圆形四立柱涡激运动的流向幅值非常小，这与经典单圆柱涡激运动的结果相类似。图3给出了两种统计方法下圆形四立柱涡激运动横向振幅的统计结果，从整体上看两种统计方法下横向振幅随折合速度的变化规律基本一致，只是标称振幅统计法的结果略微小于最大振幅统计法的结果，这说明圆形四立柱涡激运动横向运动的规则性。圆形四立柱涡激运动横向振幅要比流向振幅大一个量级，在折合速度到达8.0之前，横向振幅随着折合速度的增加不断上升，直到达到最大值1.99D，远大于圆形四立柱的流向最大值0.26D。横向振幅幅值跳跃的拐点和流向振幅幅值的拐点相同，都出现在折合速度为9.0时。经典单圆柱涡激运动的幅值跳跃点出现在整个系统刚经过锁定区间时，本文圆形四立柱涡激运动系统也是在刚经过频率锁定区间后出现幅值跳跃现象，后面将详细阐述。

图2　不同折合速度下流向振幅 Fig.2 Stream-wise amplitude with reduced velocity

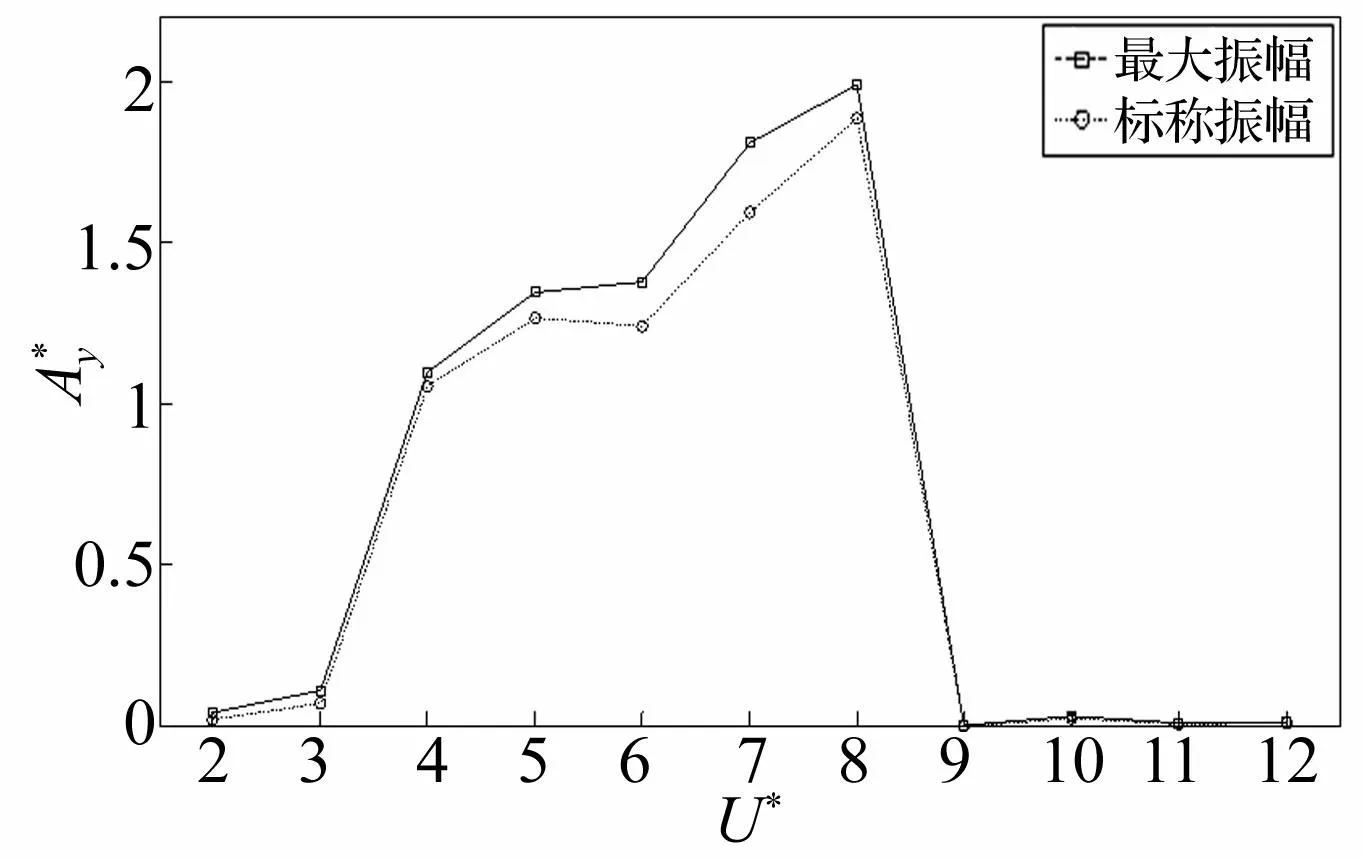
图3　不同折合速度下横向振幅 Fig.3 Transverse amplitude with reduced velocity

图4分别给出了圆形四立柱在不同折合速度下流向位移x/D和横向位移y/D时历曲线，以及对升力系数进行的谱分析结果。快速傅里叶变换可以将数值模拟得出的升力系数相对时间的函数得出系统能量在不同频率上的密度分布，从而将时域计算结果转到频域上面来分析。时历曲线图笔者截取了100s-500s范围内的稳定阶段，其纵坐标为系统达到稳定状态时位移和立柱特征长度的比值。从图4可以看出，系统的流向位移和横向位移曲线在各折合速度下的简谐性比较好，横向运动的周期是流向运动周期的两倍。从图4(a)～4(c)可以看出圆形四立柱涡激运动升力系数谱能量比较集中，当折合速度比较大时，见图4(d)，系统能量极值不只一个，这表明此时系统处于多频振动模式。图5给出了圆形四立柱涡泄频率随折合速度变化的趋势图，其中f*代表泻涡频率与圆形四立柱固有频率的比值。当泻涡频率和其固有频率接近时，系统会发生共振现象。若在一定折合速度范围内泻涡频率随定在柱体的固有频率，即发生锁定现象。从图5中可以看出，在折合速度为5.0～8.0时，涡泄频率都锁定在0.0513Hz，与其固有频率0.061Hz比较接近，圆形四立柱涡激运动有着明显的频率锁定现象，这与经典单柱涡激运动的研究结果类似。当折合速度经过频率锁定阶段，泻涡频率随着折合速度的增加急剧上升。

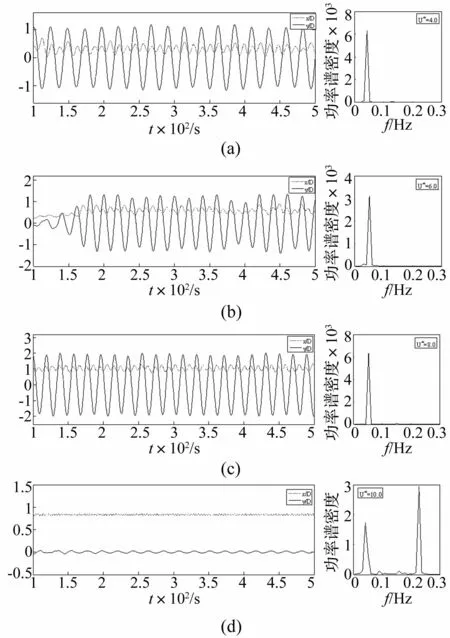
图4　不同折合速度下x/D和y/D时 历曲线图与升力系数谱分析 Fig.4 Time history of x/D and y/D with reduced velocity, FFT analysis of total lift coefficient

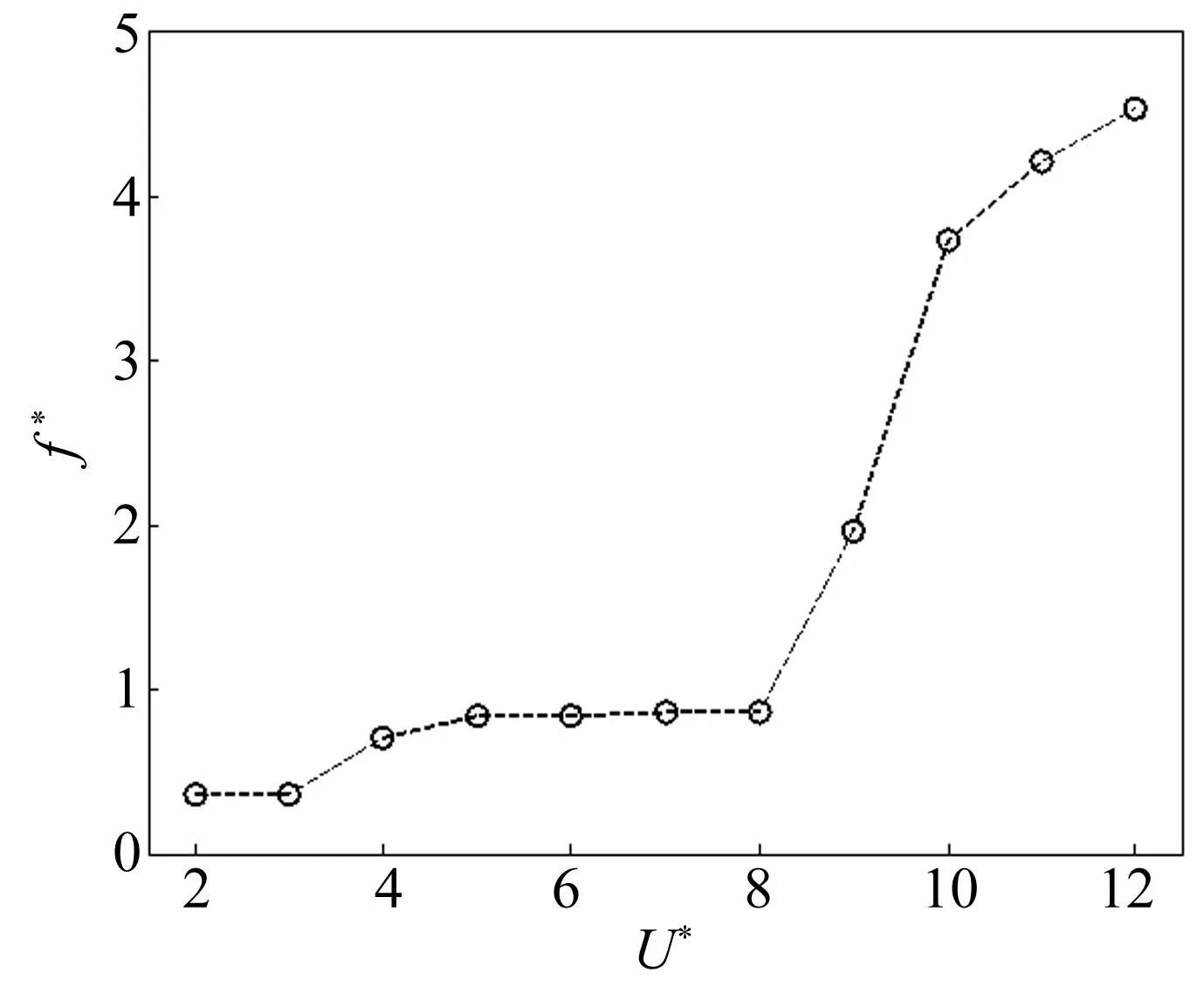
图5　不同折合速度下涡泄频率 Fig.5 Frequency response with reduced velocity

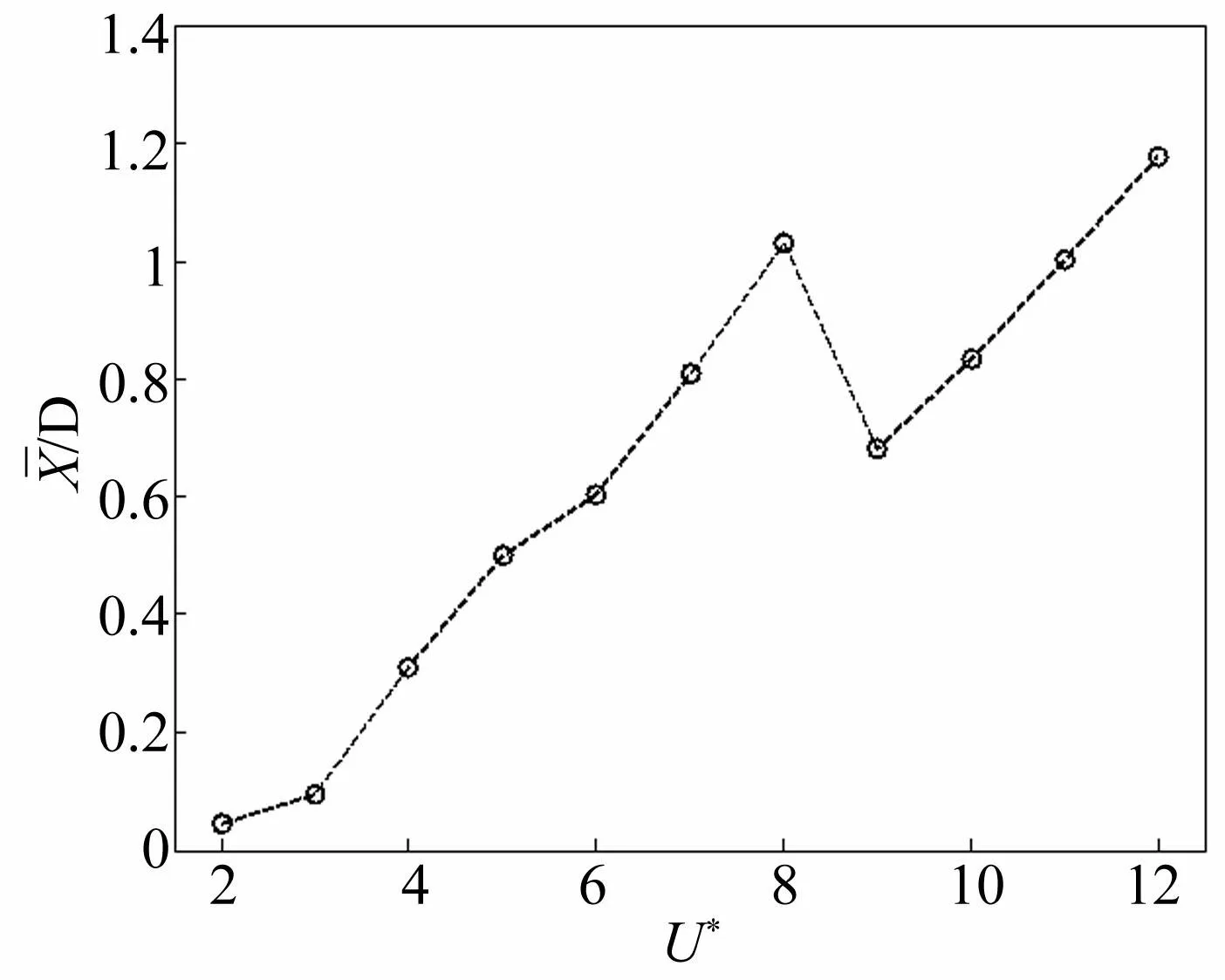
图6　不同折合速度下流向平衡振幅 Fig.6 The equilibrium postion of stream-wise oscillation

值得注意的是，圆形四立柱流向运动平衡位置随折合速度增大并不是一直增大，出现了拐点，见图6。在折合速度不大于8.0时，圆形四立柱的平衡位置远离初始位置的距离要随折合速度的增大不断增大。当圆形四立柱刚走出锁定区间进入锁定区域后的阶段，流向的平衡位置向初始位置方向靠近，这也导致流向与横向的振幅迅速减小。流速的继续增大，使得水流对流向运动的影响进一步加大，流向平衡位置又继续远离初始平衡位置。

两自由度四立柱涡激运动的轨迹和单柱体涡激运动的轨迹并不相同，由于柱体之间的相互影响，轨迹图并没有单柱体运动轨迹的规律那么明显。影响柱体涡激运动形状的因素有很多，主要是由流向和横向振动频率的大小关系、流向和横向位移的大小及相位差。经典单圆柱涡激运动的轨迹为“8”字形，这是由于流向振动频率是横向振动频率的两倍。由于下游立柱处于上游立柱的尾流区中，柱体之间的相互干扰影响了运动轨迹的规则性，圆形四立柱的横向位移曲线和流向位移曲线简谐性比较强，另外流向的振动频率是横向振动频率的2倍，这就导致了圆形四立柱的运动轨迹出现了经典的“8”字形，但没有单圆柱的规则。在不同的折合速度下横向位移与流向位移的大小不同，这也产生了“8”字形肥瘦程度的不同，具体详见图7。

图7　不同折合速度下圆形四立柱轨迹图 Fig.7 Four cylinder column motion trace at various reduced velocity

圆形四立柱涡激运动尾涡脱落模式见图8，笔者截取了6个典型折合速度下的圆形四立柱尾涡结构图。四立柱的尾涡结构图没有单圆柱的结构图明朗，这是由于柱体之间的干扰作用，下游的两个柱体处于上游两个柱体的尾流中，上游柱体的尾流区存在涡脱落，外部剪切层卷起并进入下游柱体的尾流区，与下游柱体的尾涡合并，从而使下游柱体尾流区呈现尺度不同、秩序凌乱的涡。当立柱之间的间距比比较小时，流动干扰强烈，涡结构与脱落模式的复杂无规律导致了水动力的不规则。总的来说，圆形四立柱低折合速度下尾涡模式呈现出了P+S模式，在高折合速度下呈现出2S模式，具体见图8。

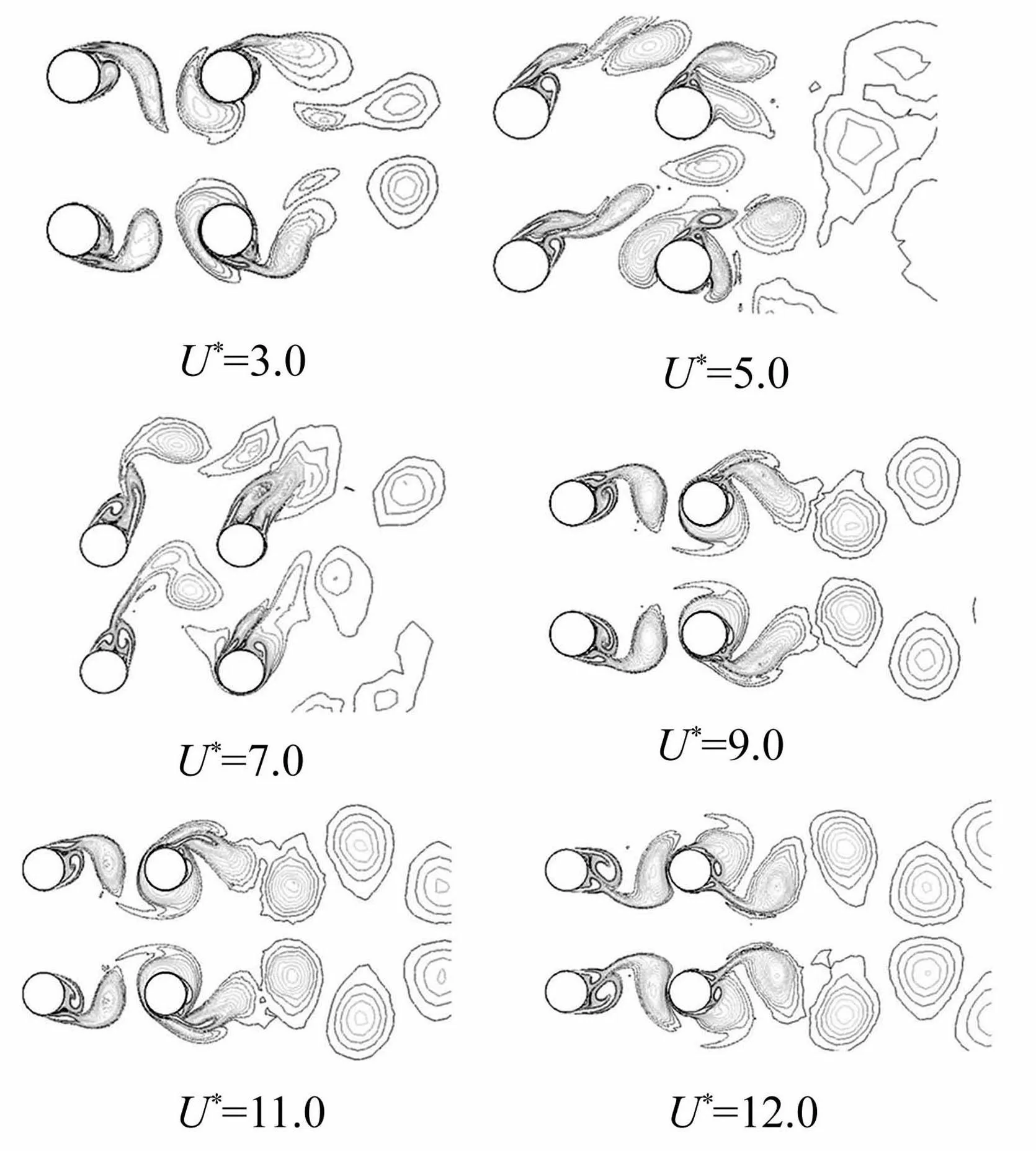
图8　圆形四立柱涡脱结构图 Fig.8 Vortex shedding mode of four cylinder column

3结论

本文采用有限体积法对圆形四立柱涡激运动进行数值模拟，着重分析圆形四立柱两向自由度的幅值响应、频谱特性、运动轨迹和尾涡脱落模式。运用四阶Runge-Kutta方法来求解结构运动微分方程，并将求解程序代码嵌入UDF中，通过DEFINE_CG_MOTION宏函数将求解出的结构动力瞬态响应传递给立柱，使用动网格技术来实现网格的更新。通过对圆形四立柱涡激运动的数值研究得出如下结论：

(1)圆形四立柱涡激运动流向和横向振幅随着折合速度的增大先增大后减小，并出现幅值跳跃现象，跳跃点在折合速度9.0处。横向振幅最大值出现在折合速度为8.0时，大小为1.99D，远大于流向振幅最大值0.26D。圆形四立柱流向运动平衡位置随折合速度增大并不是一直增大，在折合速度9.0时突然下降随后增大。

(2)圆形四立柱涡激运动出现了明显的频率锁定现象，锁定区间为5.0-8.0。当系统走过锁定系统后，流向幅值和流向幅值迅速减小。

(3)在不同折合速度下圆形四立柱涡激运动轨迹出现了经典的“8”字形，肥瘦程度各异，其形状主要由振动频率、相位差和位移等决定，但圆形四立柱涡激运动没有单圆柱运动轨迹规则。圆形四立柱低折合速度下尾涡模式呈现出了P+S模式，在高折合速度下呈现出2S模式。

参考文献

[1]Sumner D, Richards M D. Some vortex-shedding characteristics of the staggered configuration of circular cylinders [J]. Journal of Fluids and Structures, 2003, 17(3): 345-350.

[2]Sumner D. Closely spaced circular cylinders in cross-flow and a universal wake number [J]. Journal of Fluids and Structures, 2004, 126: 245-249.

[3]Sumner D, Richards M D, Akosile O O. Two staggered circular cylinders of equal diameter in cross-flow [J]. Journal of Fluids and Structures, 2005, 20(2): 255-276.

[4]Price S J, Païdoussis M P, Krishnamoorthy S. Cross-flow past a pair of nearly in-line cylinders with the upstream cylinder subjected to a transverse harmonic oscillation [J]. Journal of Fluids and Structures, 2007, 23(1): 39-57.

[5]Lam K, Jiang G D, Liu Y, et al. Simulation of cross-flow-induced vibration of cylinder arrays by surface vorticity method[J]. Journal of Fluids and Structures, 2006, 22(8): 1113-1131.

[6]Lam K, Zou L. Experimental study and large eddy simulation for the turbulent flow around four cylinders in an in-line square configuration[J]. International Journal of Heat and Fluid Flow, 2009, 30(2): 276-285.

[7]Lam K, Zou L. Three-dimensional numerical simulations of cross-flow around four cylinders in an in-line square configuration[J]. Journal of Fluids and Structures, 2010, 26(3): 482-502

[8]Anagnostopoulos P, Dikarou C. Numerical simulation of viscous oscillatory flow past four cylinders in square arrangement[J]. Journal of Fluids and Structures, 2011, 27(2): 212-232..

[9]Bao Y, Wu Q, Zhou D. Numerical investigation of flow around an inline square cylinder array with different spacing ratios[J]. Computers & Fluids, 2012, 55: 118-131.

[10]万德成. 二维多圆柱涡激运动的数值模拟[C]//第二十一届全国水动力学研讨会暨第八届全国水动力学学术会议暨两岸船舶与海洋工程水动力学研讨会文集.2008,214-219.

[11]徐枫，欧进萍，肖仪清. 正方形顺排排列四圆柱涡激振动数值模拟[C]//第十四届全国结构风工程学术会议论文集 (下册).2009.

[12]徐枫，欧进萍. 正三角形排列三圆柱绕流与涡致振动数值模拟[J]. 空气动力学学报,2010, 28(5): 582-590.

XU Feng, OU Jin-pin.Numerical simulation of vortex-induced vibration of three cylinders subjected to a cross flow in equilateral arrangement[J]. Acta Aerodynamica Sinica, 2010, 28(5): 582-590.

[13]Ming Z, Cheng L. Numerical simulation of vortex-induced vibration of four circular cylinders in a square configuration.Journal of Fluids and Structures,2012,31:125-140.