基于方差贡献率的泄流结构多测点动态响应融合方法研究

基于方差贡献率的泄流结构多测点动态响应融合方法研究

李火坤1,刘世立1,魏博文1，黄锦林2,符晓3

(1.南昌大学建筑工程学院,南昌330031; 2.广东省水利水电科学研究院,广州510635;3.华东勘测设计研究院，杭州310014)

摘要：泄流结构不同测点的振动信号频率成分和噪声水平不尽相同，通过信息融合，可将多测点振动信号融合为一个能准确、全面反映结构整体振动特性的振动信号。针对传统数据融合算法对信号相似度要求高以及固定融合系数的缺陷，提出了基于方差贡献率的结构动态响应数据融合算法，不同时间的融合系数随该点的方差贡献率而变化，根据该时刻信息的相对重要程度动态分配权重系数，实现多测点振动信号的动态融合。通过对数学模拟信号及泄流结构原型观测动态响应数据融合结果表明：提出的动态数据融合方法能够挖掘噪声中的微弱信号，使融合后信号能够更加准确、全面的反映结构的整体振动特性；该方法与传统互相关融合算法对比表明，方差贡献率算法能够有效凸显信号中的优势频率成分，保留原信号的结构固有频率成分，具有更强的适用性。

关键词：方差贡献率；泄流结构；动态响应；数据融合

中图分类号:TV66

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.029

Abstract:The vibration signal frequency components and noise levels in multi-sensor measurement of a flood discharge structure vary with the measurement positions. These signals can be fused to a vibration signal accurately and comprehensively reflecting the vibration characteristics of the overall structure with the multi-information fusion technology. Here, aiming at traditional data fusion algorithms fixing the convergence factor and requiring higher similarity of signals, a dynamic response data fusion algorithm based on variance dedication rate was proposed. Fusion coefficient at different instants in this algorithm changed with the relative importance of the signal information. The weighting factor was dynamically allocated based on the variance dedication rate to realize the dynamic fusion of mulati-point vibration signals. The numerical signal simulation and the original measurement of the flood discharge structure dynamic response data fusion results showed that the dynamic data fusion method proposed here can excavate weak signals hidden in noise and the fused signal can reflect the vibration characteristics of the overall structure more accurately and comprehensively. The comparison between this method and the traditional cross-correlation fusion algorithm showed that this method can effectively highlight the dominant frequency components of signals, retain the structural natural frequency components in the original signals and has a stronger applicability.

Multi-point dynamic response data fusion method for a flood discharge structure based on variance dedication rate

LIHuo-kun1,LIUShi-li1,WEIBo-wen1,HUANGJin-lin2,FUXiao3(1. School of Civil Engineering and Architecture, Nanchang University, Nanchang 330031, China;2. Guangdong Research Institute of Water Resources and Hydropower, Guangzhou 510635, China;3. Huadong Engineering Corporation Limited, Hangzhou 310014, China)

Key words:variance dedication rate; flood discharge structure; dynamic response; date fusion

泄流结构的模态参数识别与动力损伤诊断是近年来的研究热点，频率和振型为结构动力损伤诊断的两大常用整体损伤因子，其中结构的固有频率是最易测得的动力参数。在泄流结构模态识别领域，由于不同测点的振动信号频率成分和噪声水平不尽相同，结构固有频率识别结果仅能精确到一定区间范围，而不是一个准确值，这不利于基于频率(或与频率有关的损伤因子)变化的动力损伤诊断。数据级信息融合技术可根据一定的理论规则将多个信号融合为一个更能反映系统真实值的信号，是最底层的融合层次，其具有数据量损失少，拥有其他融合层次所不能提供的全面、细微信息等优点。近年来，信息融合技术已应用于多个领域，研究较为活跃；Hall[1]详尽论述了数据融合的基本模型、术语、算法以及应用；Ren[ 2]提出了一种多传感器测量数据一致性融合方法, 该方法定义了一种置信概率距离来衡量传感器测量数据之间的支持程度，以此为依据实现数据之间的最优融合；焦莉[3]基于数据融合和小波分析理论，提出一种新的结构损伤诊断方法，采用改进的一致性算法融合多传感器的测量数据，克服了一致性算法中两传感器在测量精度不同时置信距离不同的缺点，对支持矩阵进行模糊化处理，避免了人为定义阈值而产生的主观误差；李学军[4]在相关函数[5～6]的基础上提出了互相关融合算法，该算法可自动筛选有效传感器提供的信息，排除失效传感器，实现有效信息之间的准确识别；Escamilla-Ambrosio[7]将模糊逻辑和Kalman滤波相结合，建立了集中式、分布式和混合式的自适应Kalman滤波多传感器融合算法；卢伟[8]将数据融合方法应用于传感器优化布置，提出了基于数据融合的传感器优化布置方法；谢志江[9]将数据融合技术引入机械故障诊断中，并研究了多传感器数据融合的层次和模型；姜绍飞[10]提出一种基于模态指标和数据融合的结构损伤识别方法，该方法在钢管混凝土拱桥上得到验证；胡鑫[11]提出了一种基于振动响应内积向量和数据融合的损伤检测方法，以响应点间的内积向量作为损伤指标，利用证据理论将各结构各参考点下的损伤指标进行融合，较为准确的进行了损伤定位。

从现有的研究成果来看，数据融合技术作为独立的主要技术手段被广泛引入到结构损伤诊断方法中，在损伤诊断过程中有着明确的数据融合算法，目前利用数据融合技术进行结构损伤诊断的研究主要集中在特征级融合上，决策级融合和数据级融合的研究相对较少[12]。数据级融合最大地保留了原始数据的特性，目前多数传统数据级融合算法对多传感器信号相似度要求高并且固定融合系数，对于泄流结构振动响应信号的融合存在不适定性，针对上述不足，本文提出了基于方差贡献率的泄流结构动态响应数据融合算法，通过数学模拟的方式，从三个方面(准确性、全面性以及密频结构融合)探讨了该算法的鲁棒性和普适性，并以蜀河闸墩结构原型观测数据为例研究了该算法在泄流结构多测点信号融合的应用。结果表明：该算法能够有效利用不同测点信号的相关性、互补性和冗余性，使融合后的信号保留了结构的整体振动特性，其动态融合模式更加灵活。

1基本理论

2.1方差贡献率动态融合算法的提出

应用数据融合技术可将多测点振动信号融合为一个具有结构整体振动特性的信号，传统数据融合算法多以数值模拟的形式例证其有效性，其中多传感器振动信号通常是在真实值的基础上加以不同量的噪声形成的，因此，多测点信号具有较高的相似性。由于在融合过程中高信噪比振动信号共有的真实成分相互支持，分配较大的融合系数，而无规律的随机噪声得到削弱，使得融合后的值更加准确。

对处于泄流、发电装置等复杂噪声环境的大型泄流结构，泄流往往只能激振起结构少数几阶低频成分，而且不同部位的频率成分及振动幅值不尽相同，甚至差异很大；基于传统加权算法融合后的信号，在某些共有的频率成分识别上会更加准确，但另一些不被支持的有效信号往往被误判为噪声削弱，致使有效信息丢失，出现漏频现象。因此，如何提取信号的有效信息，避免结构固有频率成分丢失，是实现泄流结构多测点信号融合的关键。因此提出以方差贡献率为依据，根据信息的重要性分配融合系数，实现多传感器信号的动态融合算法，可有效避免信号有效信息的丢失。

1.2方差贡献率的定义

设某传感器以某一采样频率在采样时间t内采集到一个数据序列信号(含m个振动数据)，其离散信号值分别为x1,x2,...,xi,...,xm。

定义：点xi对时间t内采集的数据序列的方差贡献率为：

(1)

当有n个同类传感器在一定时长内同时采集m个振动数据时，设传感器i采集的第j个数据为xij，则根据式(1)，其方差贡献率可写为：

(2)

(1)选择具有有效频率成分的振动信号，基本原则为频谱图具有较明显的峰值，对信号信噪比要求不高。

(2)将各个测点的离散信号能量归一化。由于边界条件等因素的影响，泄流结构不同部位振动能量存在很大差异，能量归一化使不同测点振动信号在同一标准下比较其信息的相对重要性。

(3)计算能量归一化后各个测点信号的均值与方差。

(4)根据式(2)计算选定信号每个离散点的Kij。Kij随不同的xij而变化，而xij为传感器采集的振动数据，其值随时间t变化，因此，Kij可视为随时间t变化的物理量。

根据不同测点信号某时刻数据的方差贡献率，传感器i采集的第j个数据xij分配的融合系数aij为：

(3)

则数据融合后j点的值xj为：

(4)

由于信号不同点数据的方差贡献率不同，使得融合系数随时间而变化，因此，方差贡献率算法是一种能够自动筛选信号重要信息的多传感器动态数据融合方法。

2方差贡献率动态融合算法数学信号模拟验证

为验证基于方差贡献率的泄流结构多测点动态融合算法的可行性，根据数据融合的特点以及泄流结构原型观测数据信号处理及多测点模态识别中常遇到的问题，分别从多测点信号融合的完整性、精确性及密频结构的多测点信号融合三方面展开论述。

3.1完整性模拟验证

泄流结构不同部位振动信号的频率成分和噪声水平不尽相同。如拱坝结构，通常其坝顶中部振幅最大，该部位振动信号具有频率成分少、阶次低的特点；而受边界条件的影响，坝肩部位振幅最小，该部位信号通常含有多个高阶频率成分。因此，不同测点信号之间存在一定的互补信息。

大型泄流结构中，水流往往只能激振起少数几阶结构低频成分，不同位置测点的振动响应信号所包含的结构频率成分和能量大小不尽相同，甚至差异很大。为验证该方法利用不同测点互补信息的能力，探索该方法融合后保留信号频率成分的完整性，模拟x1、x2、x3三个振动信号如下：

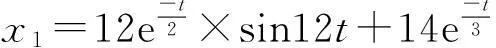
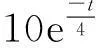
(5)

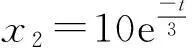
(6)

(7)

式中，t为时间，时间间隔0.01s，共10s；rand(n,M)为模拟噪声，M为样本个数。信号的时程曲线及其对应频谱图见图1～图3。

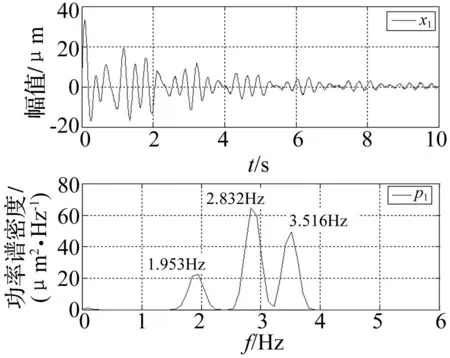
图1　信号x 1位移时程线及其频谱图 Fig.1 Time-displacement waveform and its spectrum of signal x 1

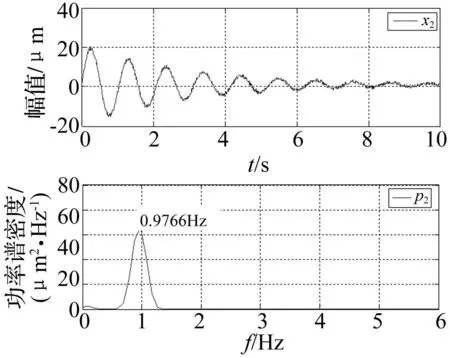
图2　信号x 2位移时程线及其频谱图 Fig.2 Time-displacement waveform and its spectrum of signal x 2

图3　信号x 3位移时程线及其频谱图 Fig.3 Time-displacement waveform and its spectrum of signal x 3

由于信号波形和模态的差异，传统数据级融合算法无法保证融合后信号频率成分的完整性，易出现漏频的现象；因此本文在完整性模拟验证信号选取时，考虑了同一结构不同测点信号包含不同频率成分及信号波形相似性问题。其中信号x2和信号x3的频率成分均为0.9766Hz，具有相似的波形；信号x1含有三阶不同于x2、x3的频率成分(分别为1.953Hz、2.832Hz、3.516Hz)，在波形相似性和频率成分方面均与x2、x3不同，具有普适性。

采用本文所提出的基于方差贡献率的融合方法，先计算三个信号数据的均值和方差，再根据公式(2)计算不同时刻信号各个点的方差贡献率Kij，得出三个测点信号x1、x2、x3的Kij值曲线见图4，然后根据公式(3)计算信号x1、x2、x3的融合系数aij，其值随时间变化见图5，最后按公式(4)实现三个信号数据的动态融合，其融合后的动位移时程线及其频谱见图6；与互相关函数融合结果以及模拟信号真实值对比见表1。

表1　融合后信号频率识别值与真实值对比

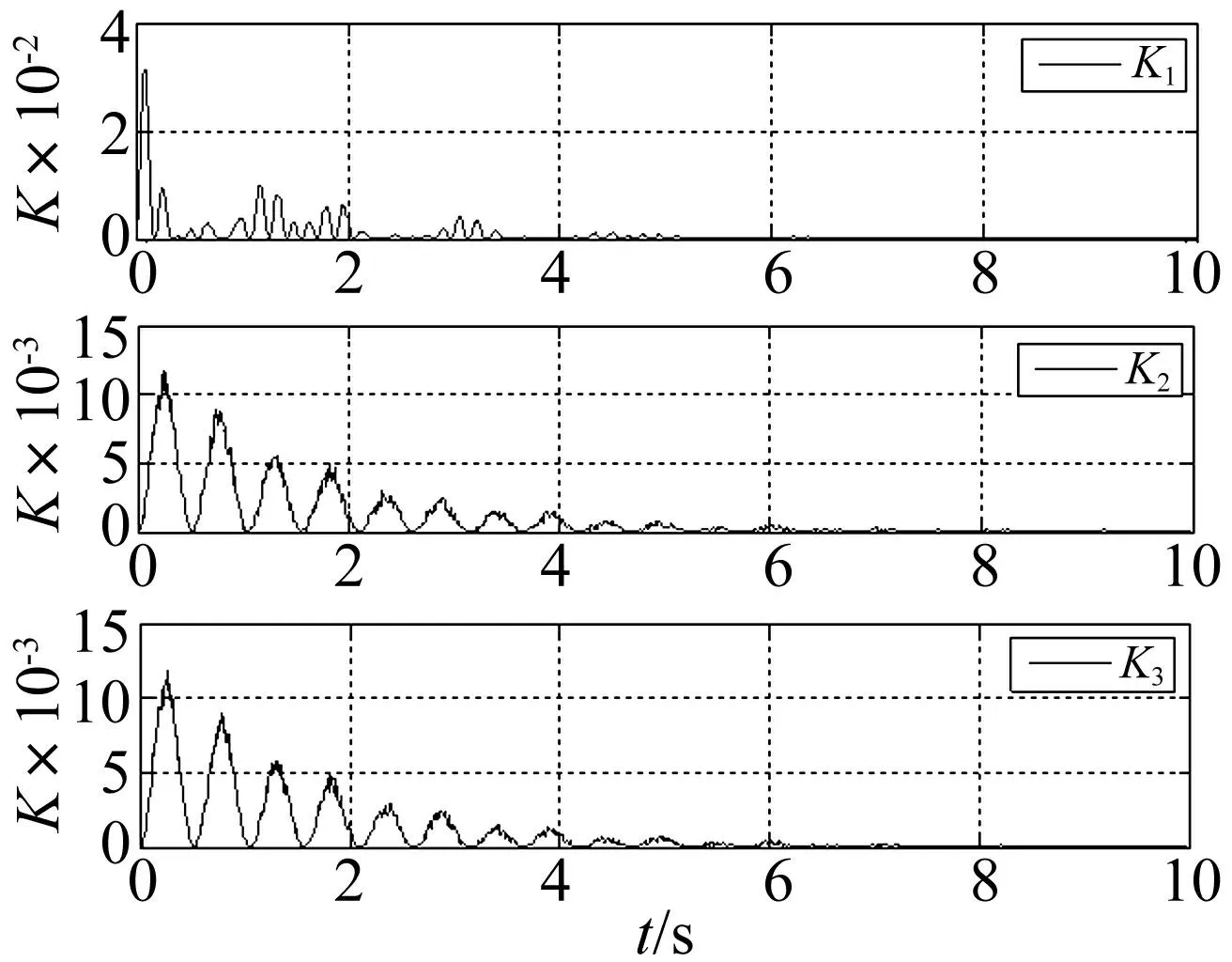
图4　方差贡献率动态曲线 Fig.4 Variance dedication rate dynamic curve

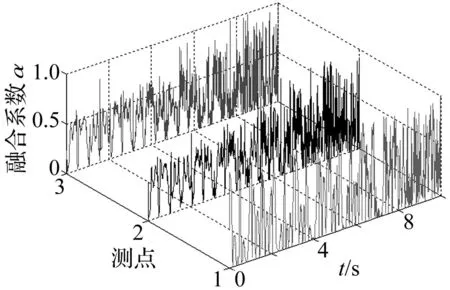
图5　融合系数动态曲线图 Fig.5 Fusion coefficient dynamic curve

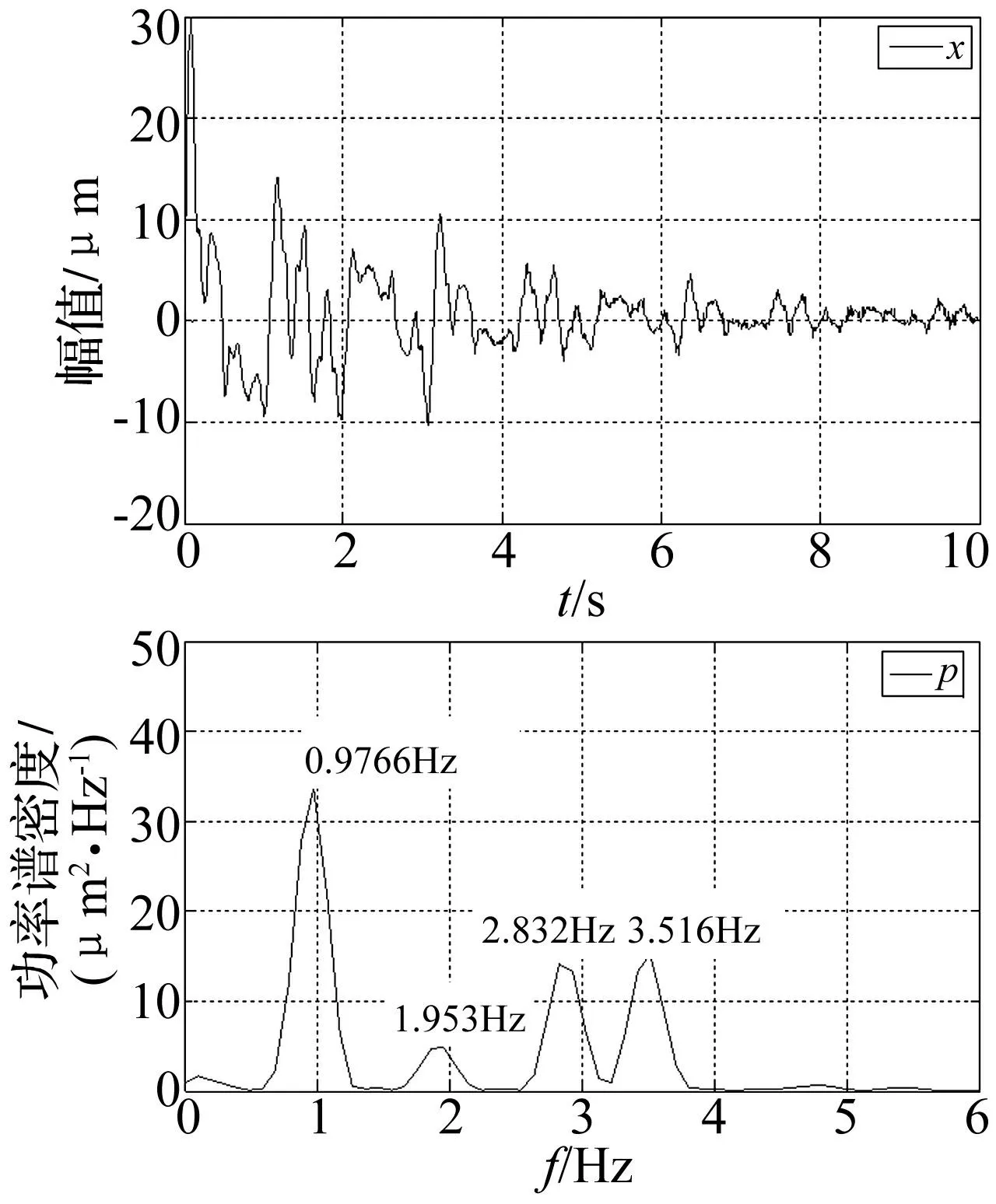
图6　基于方差贡献率动态融合的信号时程线及其频谱图 Fig.6 The fusion signal and its spectrum based on variance dedication rate

由图6及表1可知，基于互相关融合方法只提取了具有相似波形特征的信号x2、x3的频率信息(0.977Hz)，丢失了含有多阶频率的信号x1信息特征；而基于方差贡献率动态融合后的信号含有四阶频率成分，分别为0.9766Hz、1.953Hz 、2.832Hz 和3.516Hz，融合后信号完整的保留了各个测点信号的频率成分，该算法充分利用了各个测点的互补信息，使融合后信号频率成分更加完整；主要是因为方差贡献率动态融合算法具有自动提取重要信息的能力，该算法不同时间的融合系数aij随点的方差贡献率Kij而变化，根据不同时刻信息的相对重要程度动态分配权重系数，实现多测点振动信号的动态融合，因此可有效防止重要信息的丢失。

2.2精确性模拟验证

多测点信号模态识别，由于噪声的干扰，不同测点对同一阶模态的识别往往会存在一定的偏差。如文献[13]在高拱坝多测点模态识别中，频率识别结果为一定范围的区间，并且该区间随阶次升高而增大，而对于以频率准确识别为基础的动力损伤诊断和结构安全监测，频率的变化即意味着结构发生损伤。此外，多数泄流结构质量重、刚度大，在泄流激励下表现为低频微振，又有发电、水流等复杂噪声干扰，单测点的振动信号往往性噪比不高。

泄流结构多测点信号采集可视为传感器对同一对象的不同或相同方面的有关信息获取，不同传感器采集到的信号必然存在一定的相关性。为研究方差贡献率动态融合算法利用不同测点信息相关性的能力，探索该算法在结构频率准确识别的可行性，模拟具有相同频率成分但振幅不等的三个测点信号x4、x5、x6，用以反映不同频率成分能量和噪声水平，具有普适性，其表达式如下：

sin(8t)+5×rand(n,M)

(8)

sin(8t)+5×rand(n,M)

(9)

sin(8t)+5×rand(n,M)

(10)

式中，t为时间，时间间隔0.01s，共10s；rand(n,M)为模拟噪声，M为样本个数。信号的时程曲线及其对应频谱见图7～9。

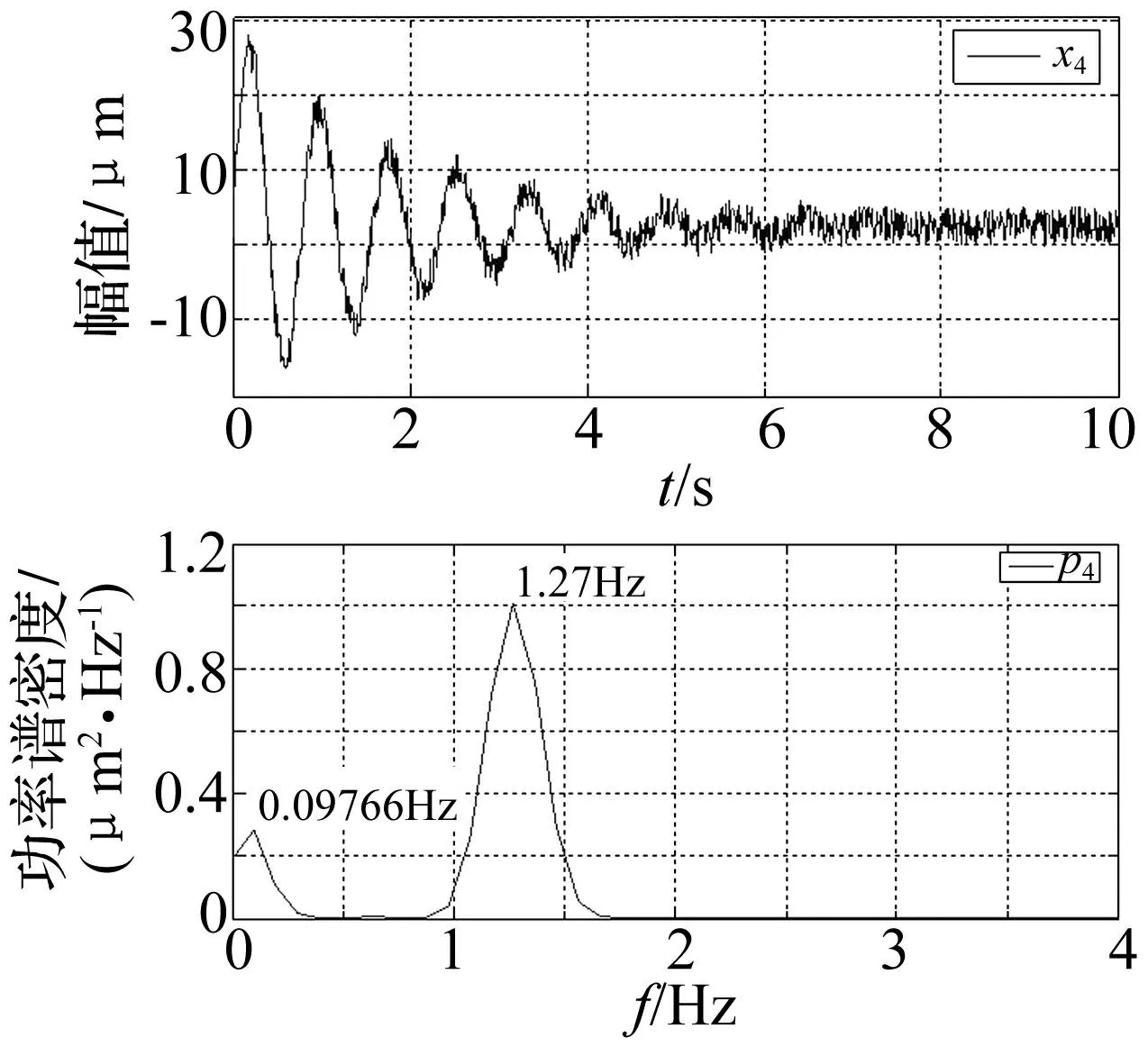
图7　信号x 4位移时程线及其频谱图 Fig.7 Time-displacement waveform and its spectrum of signal x 4

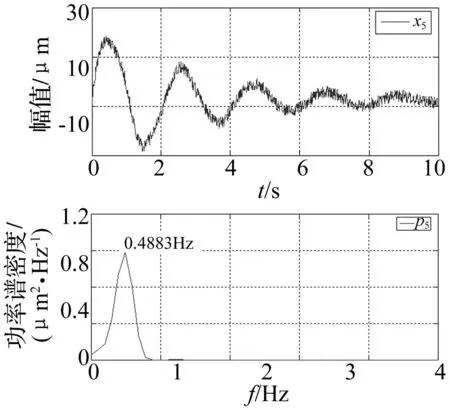
图8　信号x 5位移时程线及其频谱图 Fig.8 Time-displacement waveform and its spectrum of signal x 5

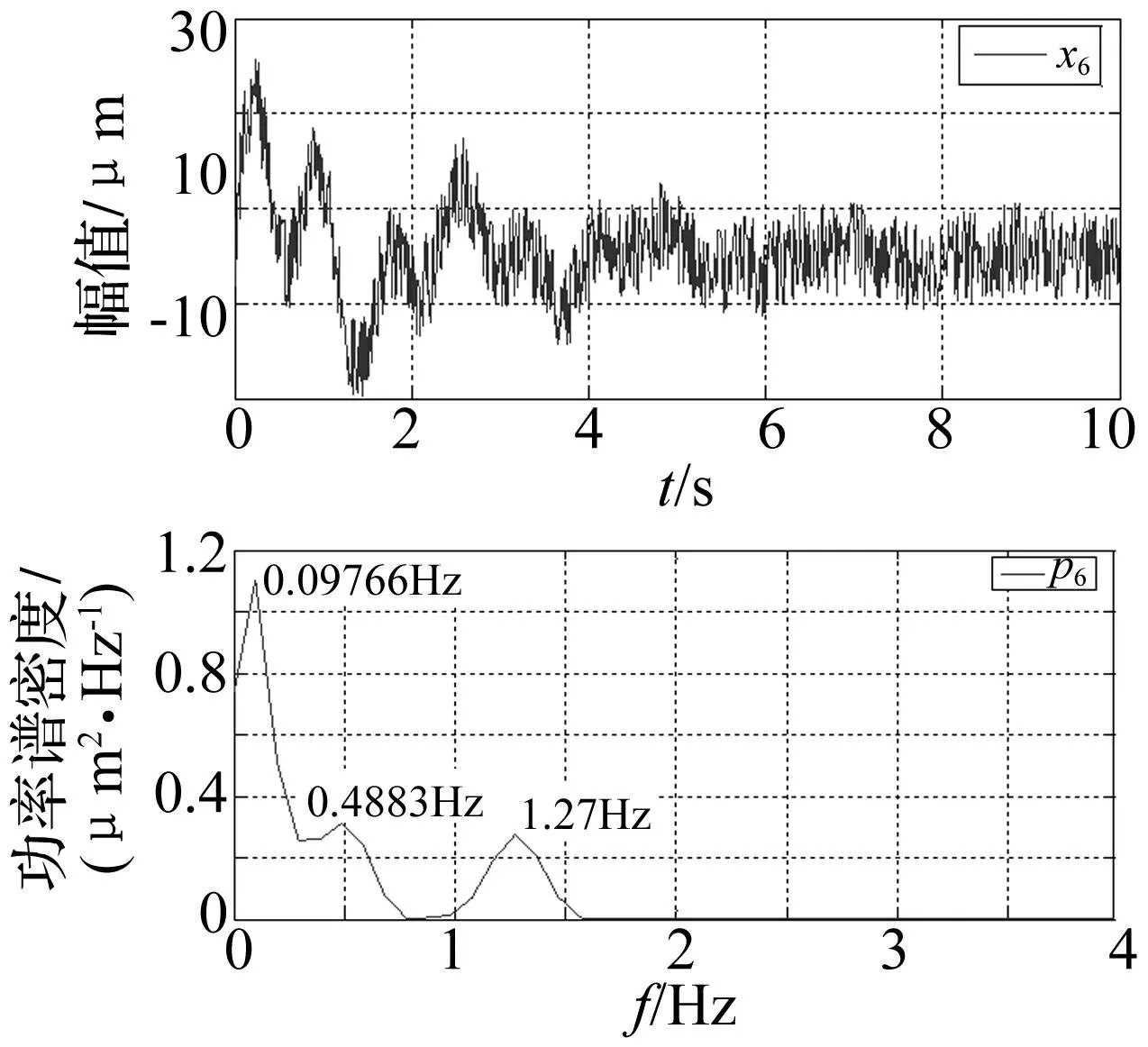
图9　信号x 6位移时程线及其频谱图 Fig.9 Time-displacement waveform and its spectrum of signal x 6

由图7～9可见，单点的频谱图识别结果与模拟信号真实频率存在一定误差，模拟信号x4、x5、x6的两阶真实频率分别为0.4775Hz和1.2732Hz，而频谱图中信号x4识别结果为0.09766Hz和1.27Hz；信号x5识别结果为0.4883Hz，仅一阶模态频率；信号x6识别结果为三阶频率，分别为0.09766Hz、0.4883Hz和1.27Hz。单点识别结果与真实值均存在一定误差，原因有两点：①振幅较小的低能量模态会被振幅较大的高能量模态淹没；②在强噪声的干扰下，低能量的模态频谱图峰值会产生一定偏差。

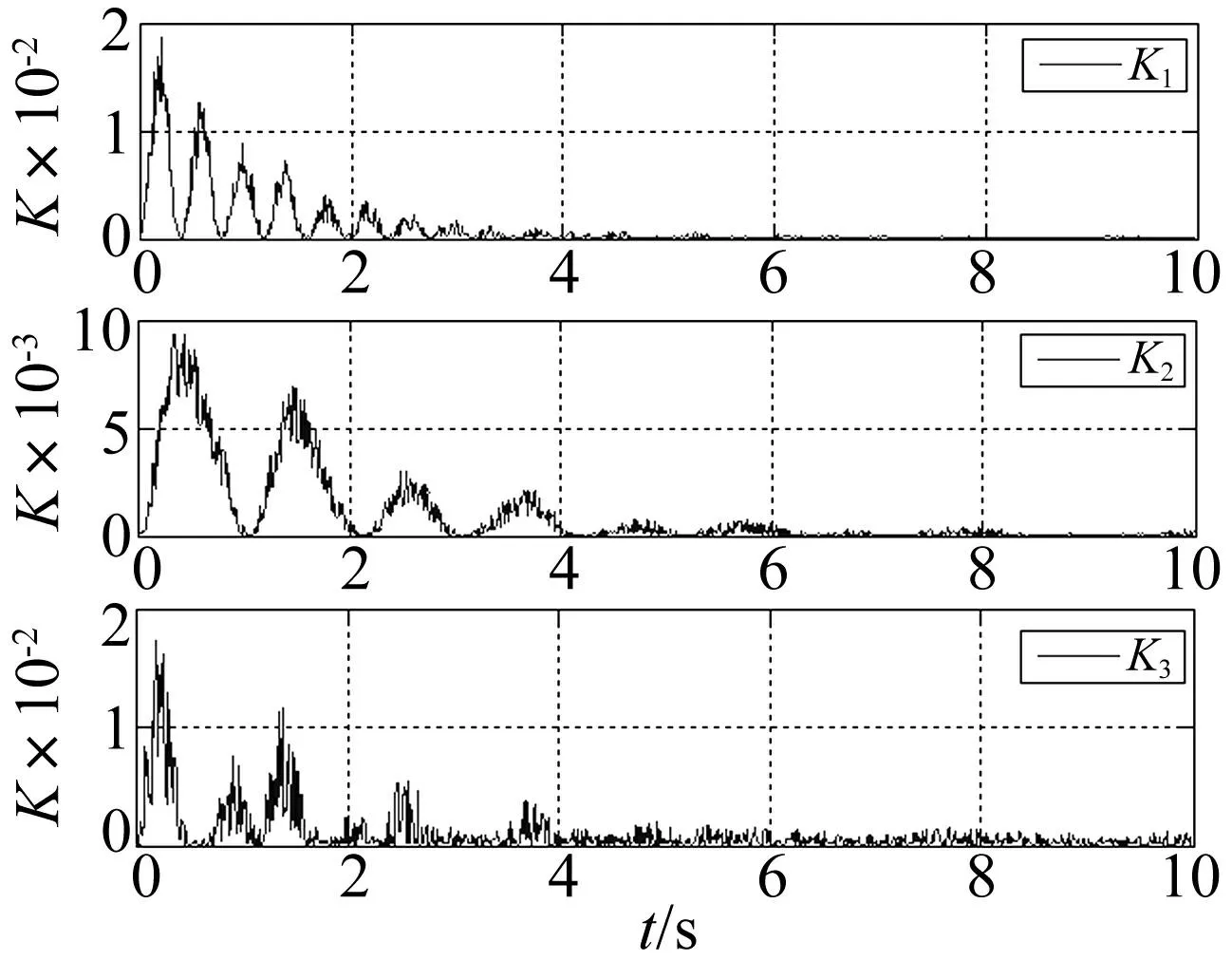
图10　方差贡献率动态曲线 Fig.10 Variance dedication rate dynamic curve

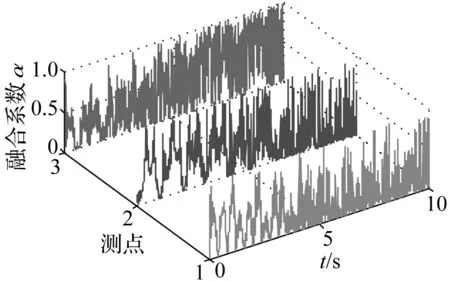
图11　融合系数动态曲线图 Fig.11 Fusion coefficient dynamic curve

图12　基于方差贡献率动态融合的 信号时程线及其频谱图 Fig.12 The fusion signal and its spectrum based on variance dedication rate

频率阶次真实值/Hz识别结果/Hz融合后信号/Hzx4x5x6x4x5x6x10.47750.09770.48830.09770.488321.27321.27/0.48831.273///1.27/

采用本文方法对信号x4、x5、x6进行融合，计算所得Kij值曲线及其融合系数aij见图10～11，融合后的动位移时程线及其频谱图见图12，模拟信号频率识别值与真实值的对比结果见表2。融合结果表明，采用方差贡献率方法进行融合后的信号含有0.4883Hz和1.27Hz两阶频率，与真实值基本相符。该算法以方差贡献率Kij为依据，根据信息的能量和相对重要性分配融合系数aij，使得融合后各个测点的高能量频率成分在融合后信号中得到充分体现，避免了低能量频率成分在噪声干扰下产生的误差，得到更加准确并保留各阶优势频率成分的动位移信号。

2.3密频成分模拟验证

部分泄流结构(如闸墩、高拱坝)在泄流激励下所表现出的振动频率通常为低频、密频；在模态参数识别时，密频成分中幅值较小、能量较低的模态容易被相邻振幅大、能量高的模态淹没。因此，结构密频成分很难在同一个信号中得到体现，致使在单测点模态识别中，往往会导致密频成分的模态丢失。因此，要使多传感器信息融合信号能够准确、全面的反映结构的整体振动特性，必须解决结构密频成分融合问题。

为验证本文方法对密频结构融合提取的可行性和适用性，模拟至少包含有两阶频率相近的信号x7、x8、x9，以体现本方法在密频结构频率提取方面的适用性，该三个测点的信号表达式如下：

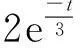
(11)

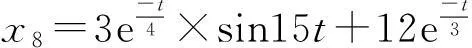
(12)

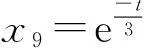
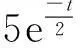
(13)

式中，t为时间，时间间隔0.01s，共10s；rand(n,M)为模拟噪声，M为样本个数；其相应的时程曲线及其对应频谱见图13～15。

图13　信号x 7位移时程线及其频谱图 Fig.13 Time-displacement waveform and its spectrum of signal x 7

图14　信号x 8位移时程线及其频谱图 Fig.14 Time-displacement waveform and its spectrum of signal x 8

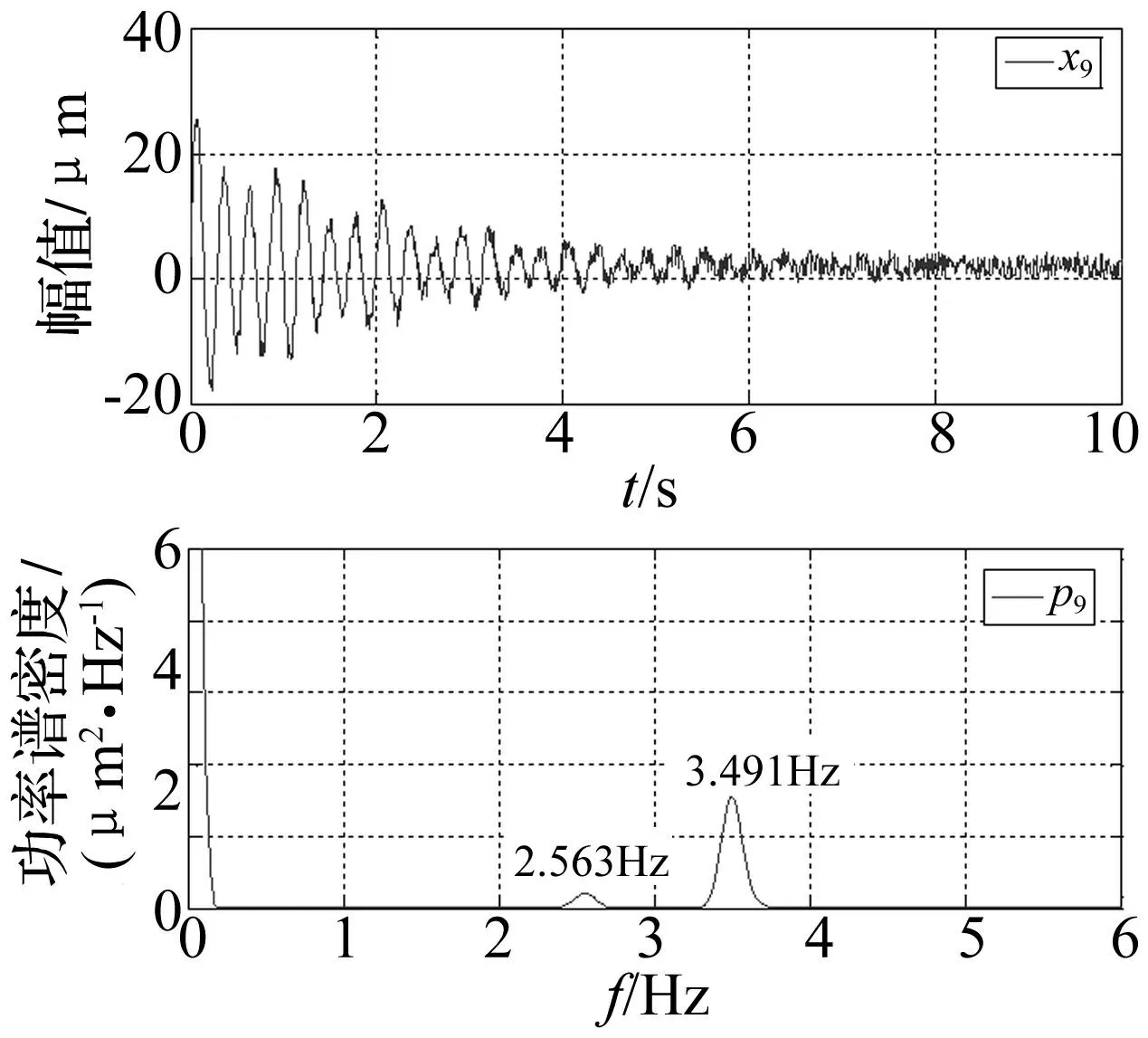
图15　信号x 9位移时程线及其频谱图 Fig.15 Time-displacement waveform and its spectrum of signal x 9

由图可见，单点信号的频谱图识别结果与模拟信号真实频率存在一定误差，模拟信号x7和x8均含有3阶模态，而识别结果仅含有两阶模态，原因是x7、x8信号中有两阶频率成分很接近，且该两阶频率的能量水平不同，在对相邻的密频信号进行频谱分析时，低能量频率成分易被高能量的相邻密频成分淹没，致使单测点频率成分丢失。

采用本文方法融合后得出信号x7、x8、x9的Kij值曲线图及其融合系数aij见图16～图17，融合后的动位移时程线及其频谱图见图18，模拟信号频率识别值与真实值的对比结果见表3。融合结果表明，基于方差贡献率动态融合的信号含有2.368Hz、2.563Hz、3.467Hz和3.687Hz四阶频率，与真实值基本相符，该方法具有较好的密频结构频率信息捕捉能力。

图16　方差贡献率动态曲线 Fig.16 Variance dedication rate dynamic curve

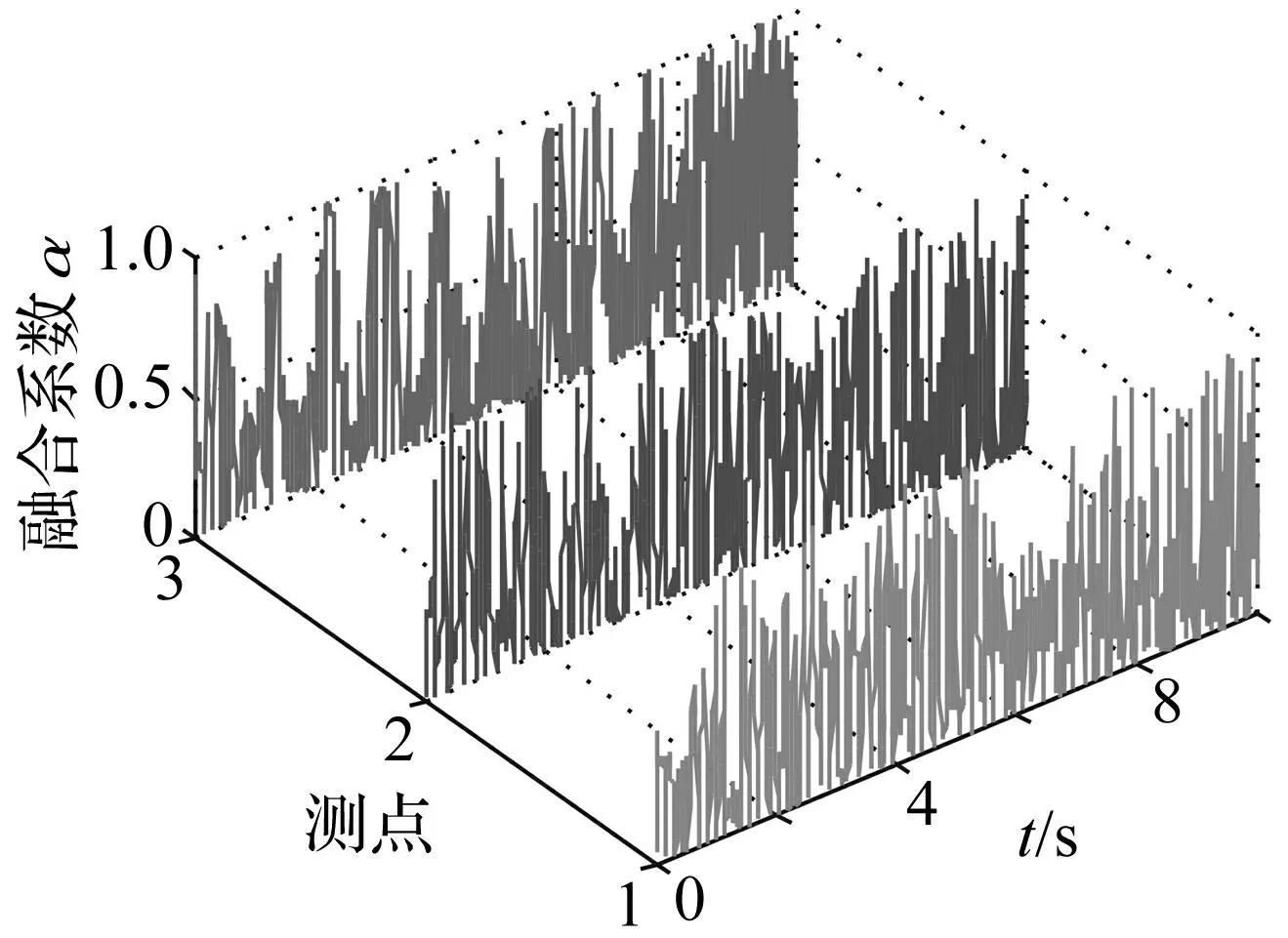
图17　融合系数动态曲线图 Fig.17 Fusion coefficient dynamic curve

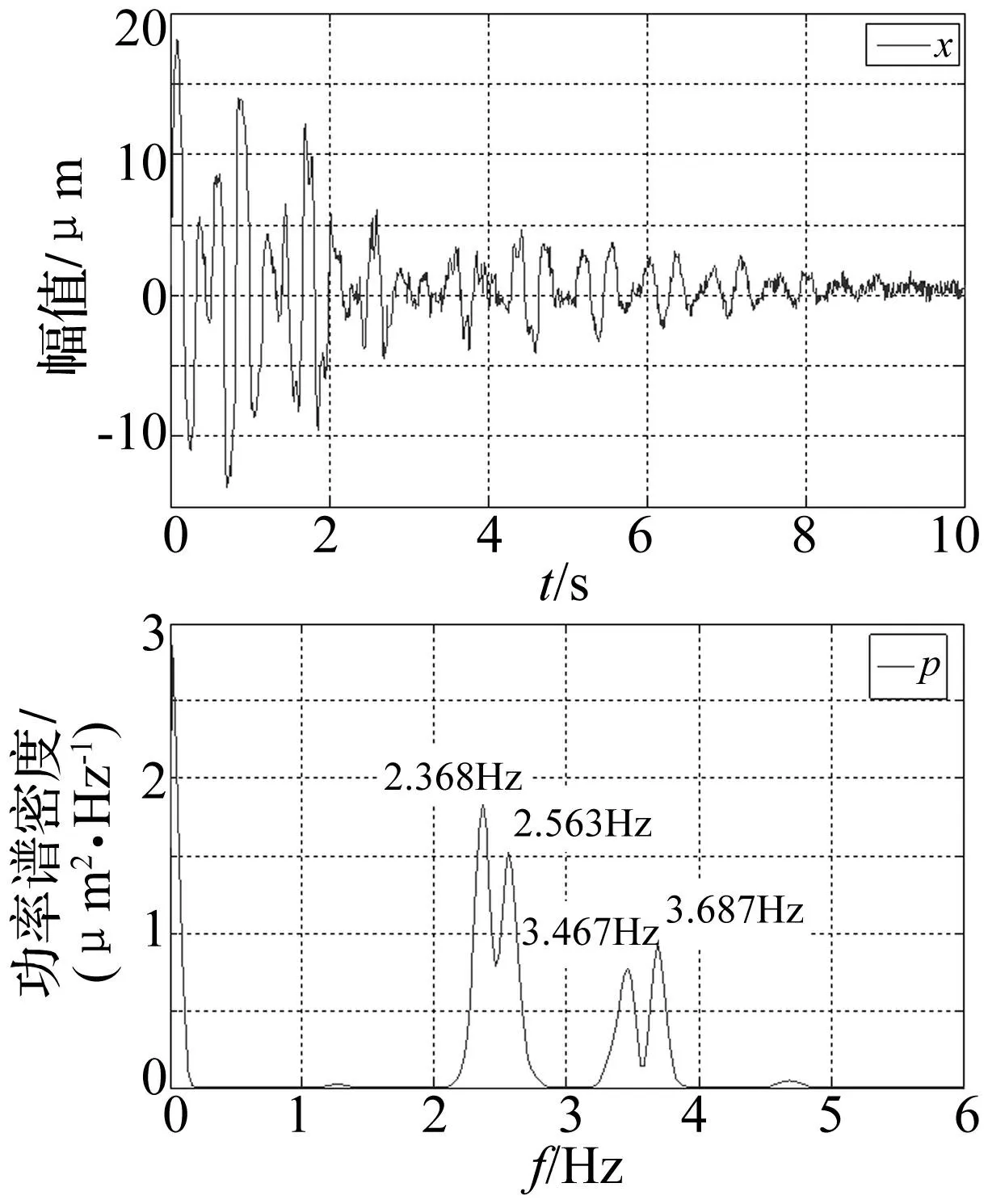
图18　基于方差贡献率动态融合算法的 动位移信号时程线及其频谱图 Fig.18 The fusion signal and its spectrum based on variance dedication rate

频率阶次真实值/Hz识别结果/Hz融合后信号/Hzx7x8x9x7x8x9x12.3872.3872.5472.3932.5632.5632.36823.5012.5473.5013.4913.6623.4912.56333.6613.661////3.4674//////3.687

3工程实例

闸墩结构多测点振动测试，通常于闸墩顶部顺水流方向依次布置多个传感器，由于上下游水位的差异、噪声水平以及边界条件的不同，不同测点的振动信号常存在很大差异，单测点振动信号仅能代表结构局部的振动特性，利用信息融合方法可将多测点振动信号融合为一个具有保留结构整体动力特性的振动信号。本节以蜀河闸墩原型观测为例，研究基于方差贡献率的闸墩结构多测点动态响应融合效果。

3.1工程概况

蜀河水电站位于汉江上游，陕西省旬阳县蜀河镇上游约1km的河段上，为汉江干流梯级水电站之一。坝址以上控制流域面积49400km2，坝址多年平均流量732m3/s。电站正常蓄水位217.3m，电站额定水头19.3m，机组单机额定流量260m3/s，电站装机容量270MW，正常蓄水位以下水库库容1.74亿m3。枢纽工程布置以河道中部纵向闸墩为界分为左、右两侧进行建筑物布置。左侧为厂房坝段，右侧为泄洪坝段。右岸泄洪建筑物共六孔，从左至右依次为1#～4#泄洪闸、垂直升船机(兼泄洪闸)、右副坝表孔。

蜀河水电站枢纽工程于2010年年底基本完工，但在2010年汛期电站尚未完工期间和2011年刚刚完工后，连续两年经历了几场大洪水(最大约30年一遇Q=24000m3/s左右)。2011年洪水期间，运行工作人员发现泄洪闸闸墩顶部出现左右振动现象，且幅度较大，为了尽快掌握闸墩的振动特性及其振动对结构安全的影响，开展了原型动力测试，以确保今后泄洪闸安全使用、电站正常运行。

3.2闸墩结构动位移原型观测

项目课题组于2012年9月2日对蜀河溢流坝2号及3号泄洪孔的闸墩进行了动位移测试，动位移测点布置图见图19，信号采集系统连接及传感器现场布置示意图见图20～图21。动位移传感器型号为DP型地震低频振动位移传感器，频响范围0.35～150Hz，灵敏度为15mv/μm，信号采集和数据处理采用北京东方振动和噪声研究所研发的DASP测试分析系统，采样频率50Hz，各传感器现场布置位置如下：

(1) 2号泄洪孔左闸墩测点布置。测点布置于闸墩顶部(高程230.00m)，共布置了六个测点，对应的桩号从上游至下游为0+00m，0+05m，0+16m，0+27m，0+39m及0+49m，在0+39m测点处布置了水平和垂向动位移传感器。

(2) 3号泄洪孔左闸墩测点布置。测点布置于闸墩顶部(高程230.00m)，共布置了4个测点，对应的桩号从上游至下游为0+00m，0+16m，0+27m，0+39m，在0+39m测点处布置了水平和垂向动位移传感器。

(3) 3号泄洪孔右闸墩测点布置。测点布置于闸墩顶部(高程230.00m)，共布置了3个测点，对应的桩号从上游至下游为0+00m， 0+16m， 0+39m，在0+39m测点处布置了水平和垂向动位移传感器。

图19　2-3号孔闸墩测点布置图(自左至右) Fig.19 Sensor placement of 2 and 3 gate pier (left to right)

图20　信号采集系统 Fig.20 Signal acquisition system

图21　传感器布置示意图 Fig.21 Sensor layout diagram

3.3基于方差贡献率的蜀河闸墩结构多测点动态响应融合

经统计分析，闸墩在库水位和下游水位分别为215.70m和202.44m，相应入库和出库流量分别为6328.00m3/s和6753.00 m3/s工况下的振动较为显著，其相应的各个闸门启闭情况为：一号闸门开度为4.7m，二号闸门开度为18.8m，三号闸门开度为10.591m，四号闸门开度为24.777m，6台机组同时发电。本文选择该工况下三号泄洪孔左、右两个闸墩测点信号进行多测点信号融合。

(1)3号左闸墩(即2号右闸墩)多测点信号融合

3号泄流孔左闸墩顶部布置了4个水平向动位移传感器，其测点序号顺水流方向依次为7、8、9、16。各个测点的动位移时程线及其频谱图见图22～图25。

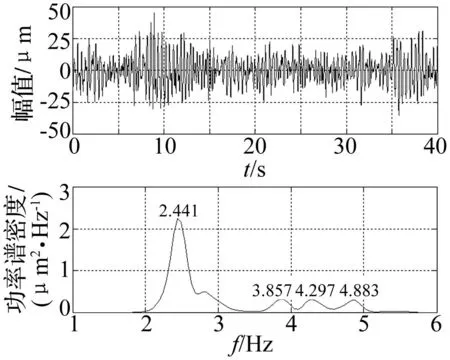
图22　测点7信号动位移时程线及其频谱图 Fig.22 Time-displacement waveform and its spectrum of test point No.7

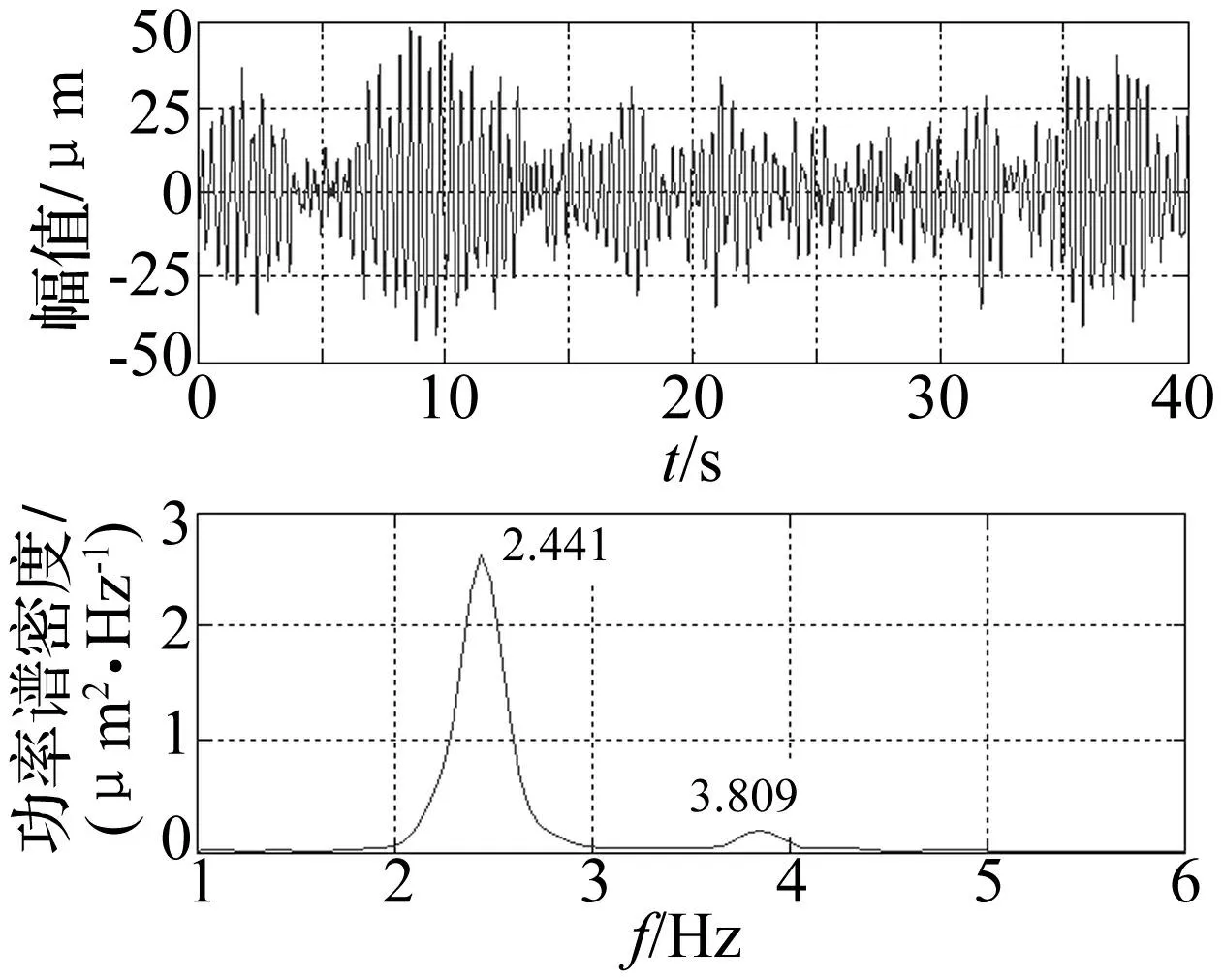
图23　测点8动位移信号时程线及其频谱图 Fig.23 Time-displacement waveform and its spectrum of test point No. 8

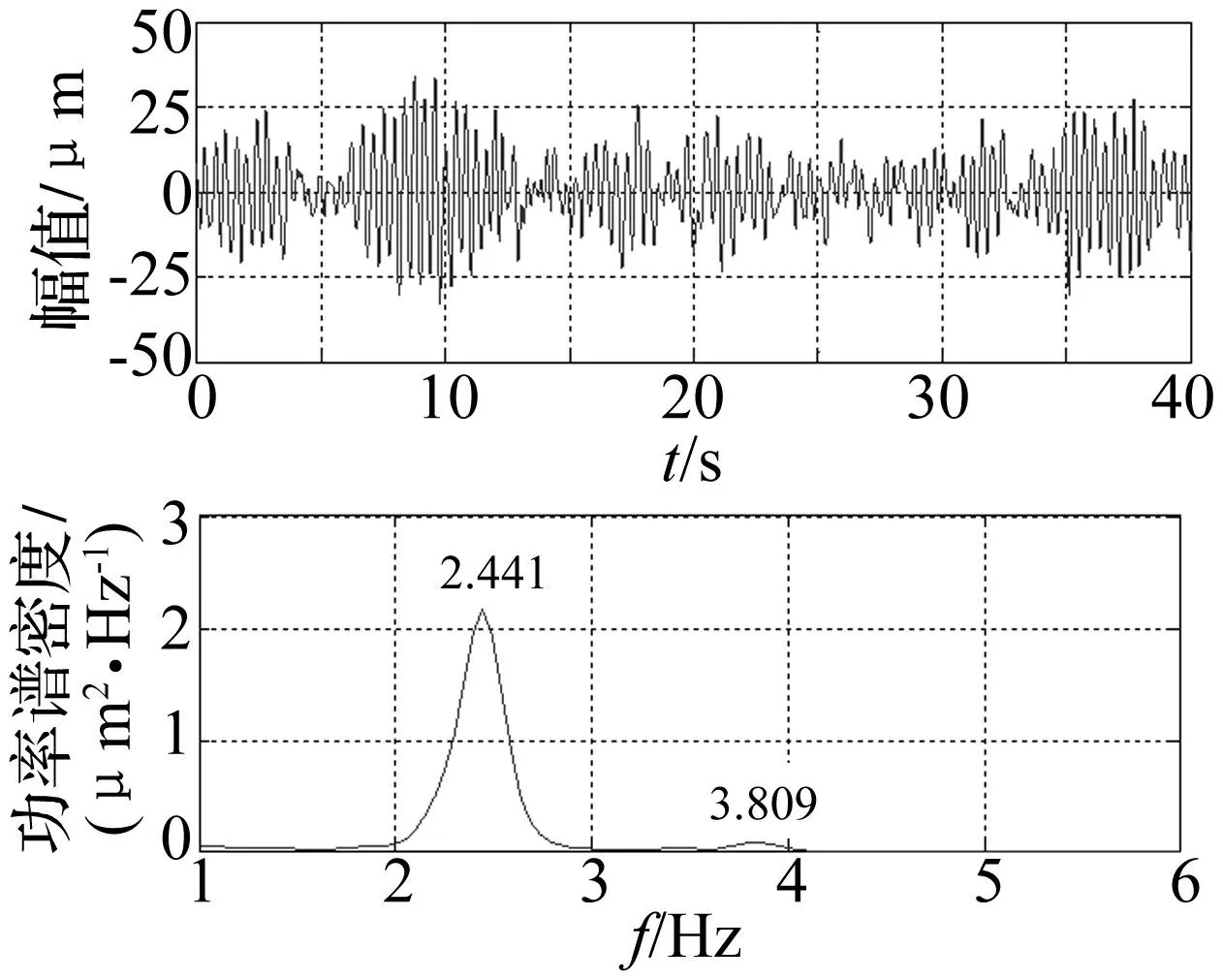
图24　测点9动位移信号时程线及其频谱图 Fig.24 Time-displacement waveform and its spectrum of test point No. 9

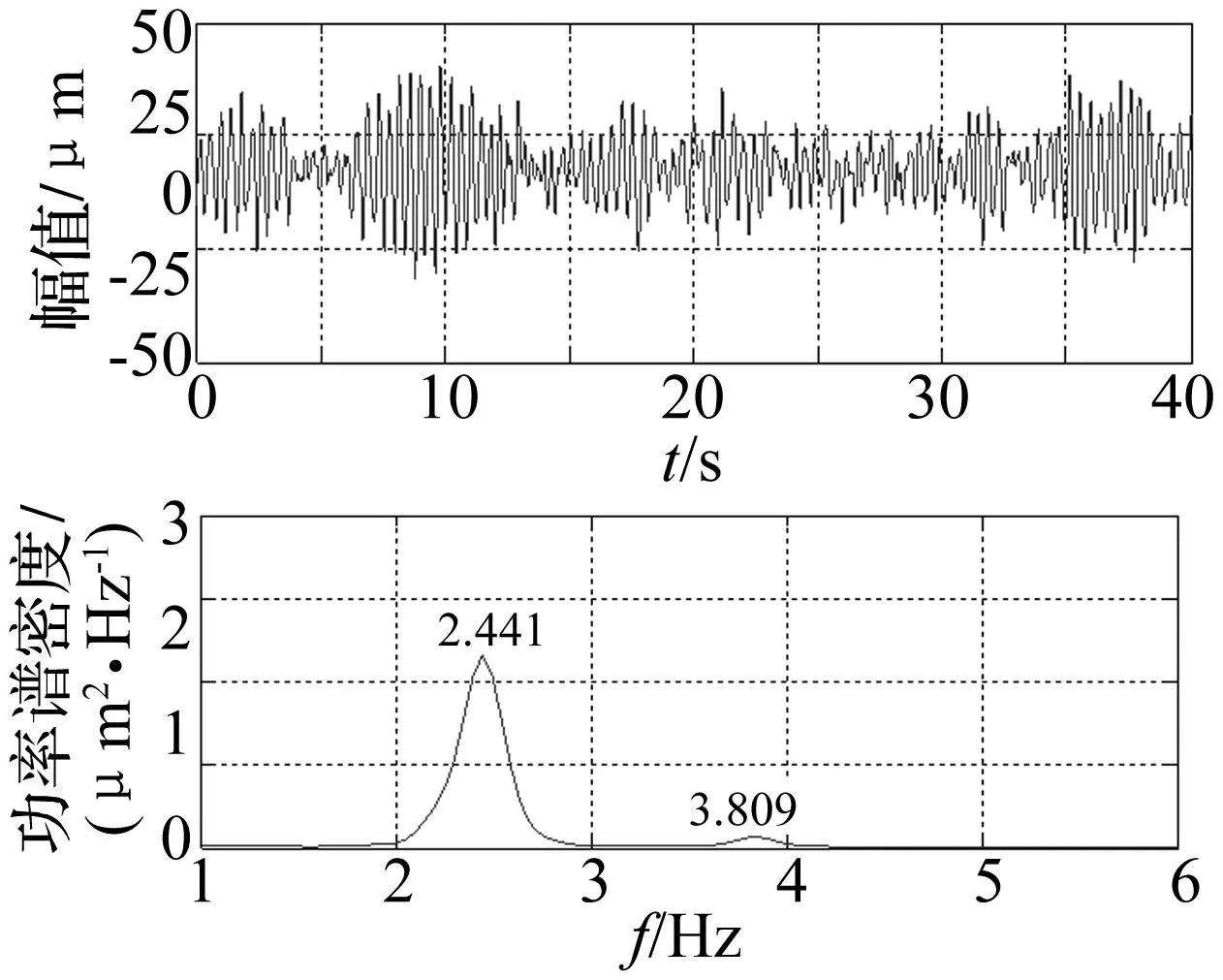
图25　测点16动位移信号时程线及其频谱图 Fig.25 Time-displacement waveform and its spectrum of test point No.16

采用本文方法计算得到四个测点信号(测点7、8、9、16)的Kij值曲线及其融合系数aij见图26～27，融合后的动位移时程线及其频谱图见图28，与基于互相关融合方法的结果对比见表4。

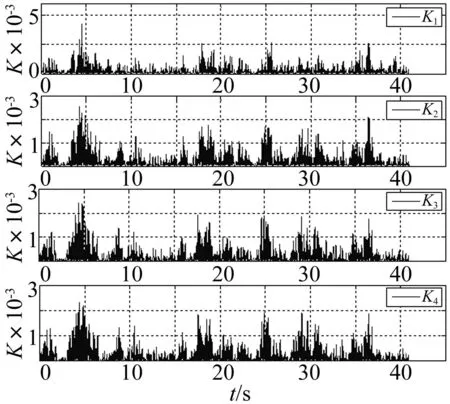
图26　方差贡献率动态曲线 Fig.26 Variance dedication rate dynamic curve

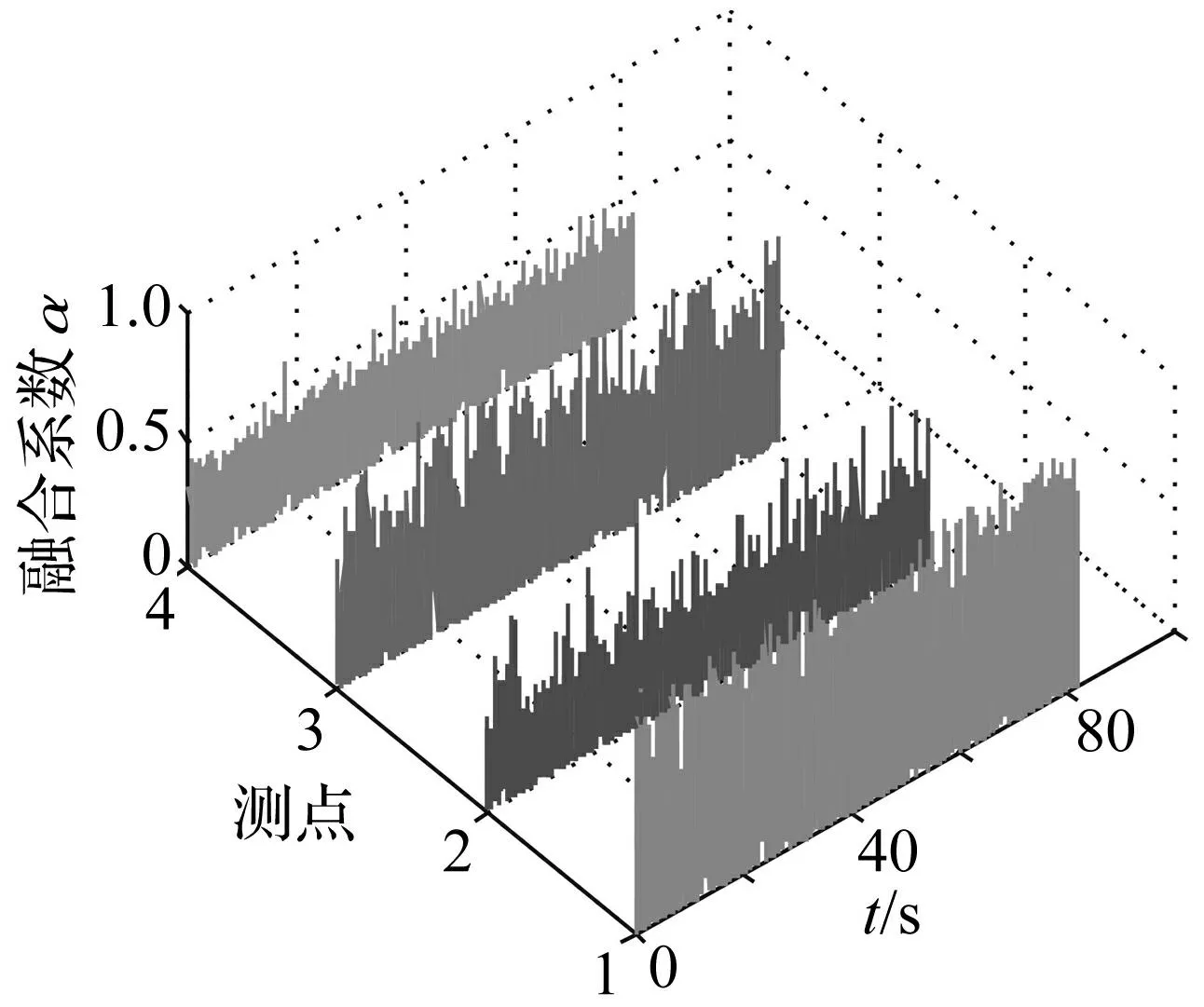
图27　融合系数动态曲线图 Fig.27 Fusion coefficient dynamic curve

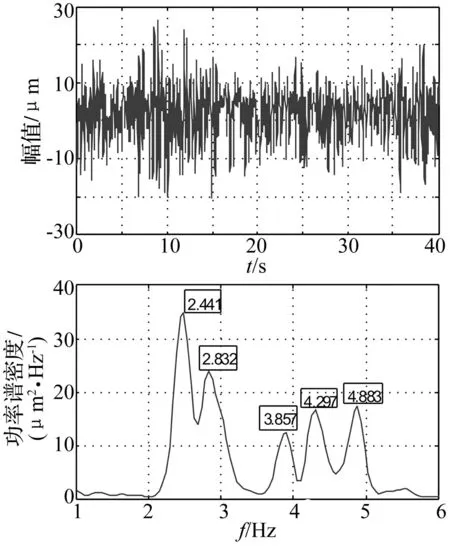
图28　基于方差贡献率动态融合信号时程线及其频谱图 Fig.28 The fusion signal and its spectrum based on variance dedication rate

融合结果表明，基于方差贡献率动态融合信号含有5阶频率，分别为2.441 Hz、2.832 Hz、3.857 Hz、4.297 Hz、4.883 Hz，该信号含有各个测点信号的频率成分，能够反映结构的整体振动特性，其中频率为2.832 Hz的振动成分在原信号中被高能量的相邻模态淹没，致使无法从单测点频谱图中准确识别，融合后信号各个频率成分含有的能量更加均衡，使得原本微弱的频率成分峰值更加清晰；测点7中频率为3.857 Hz的模态与测点8、9、16信号中频率为3.809 Hz的模态实为同一阶模态，由于噪声的影响以及其它高能量频率成分的淹没效应，不同测点对同一阶频率的识别出现了偏差的现象，融合后信号该阶模态频率具有更加明显的峰值。可见，基于方差贡献率动态融合的信号频率成分更加完整，能够更全面的反映该工况下结构的整体振动特性。

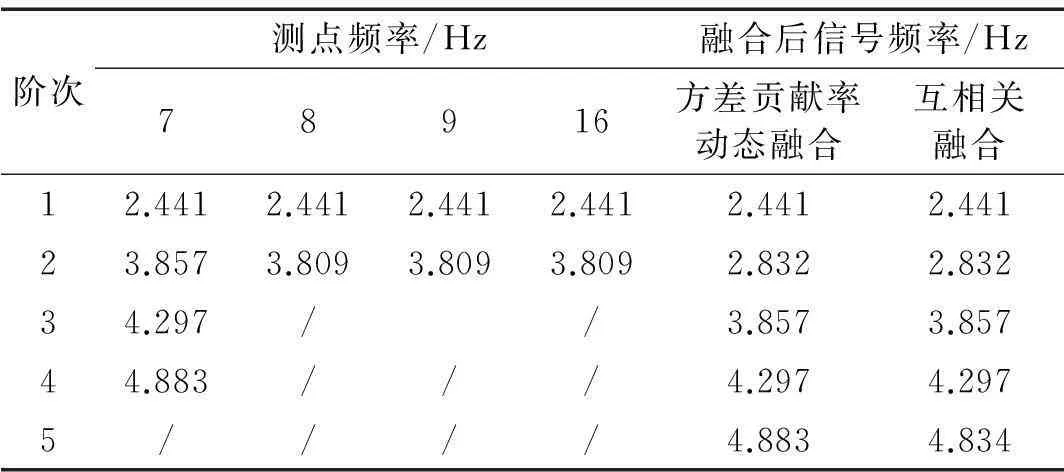
表4 频率融合结果对比

(2)3号右闸墩多测点信号融合

该水电站3号泄流孔右闸墩布置了3个水平向动位移传感器(顺水流方向测点序号依次为10、11、12)，各个测点的动位移时程线及其频谱图见图29～图31。

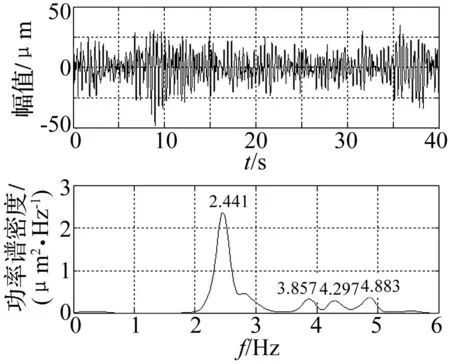
图29　测点10动位移信号时程线及其频谱图 Fig.29 Time-displacement waveform and its spectrum of test point No.10

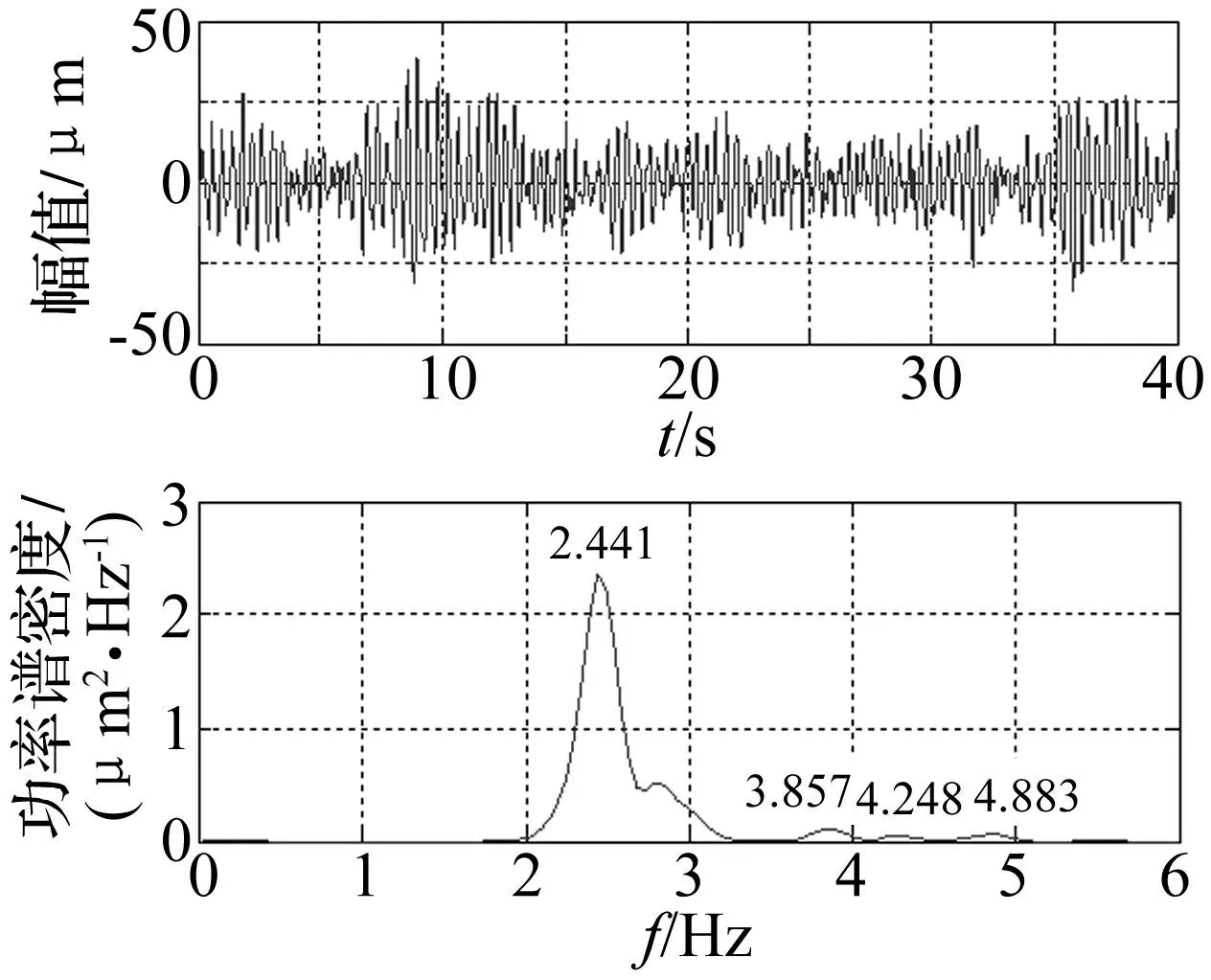
图30　测点11动位移信号时程线及其频谱图 Fig.30 Time-displacement waveform and its spectrum of test point No.11

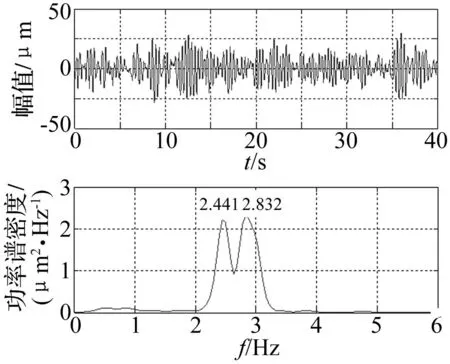
图31　测点12动位移信号时程线及其频谱图 Fig.31 Time-displacement waveform and its spectrum of test point No.12

采用本文方法得到三个测点(测点10、11、12)信号的Kij值及融合系数aij曲线图见图32～33，融合后的动位移时程线及其频谱图见图34；与基于互相关融合方法对比结果见表5。

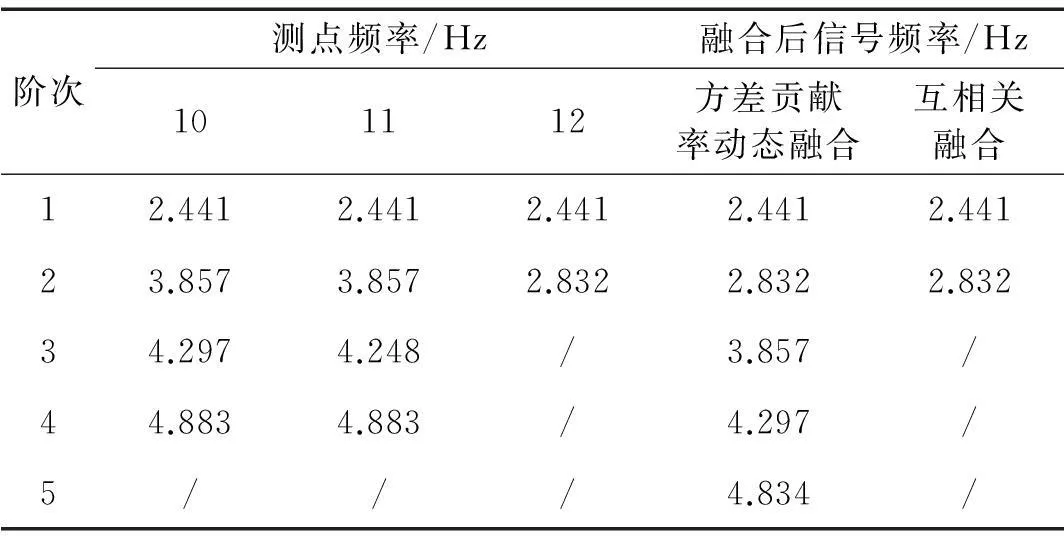
表5　频率融合结果对比

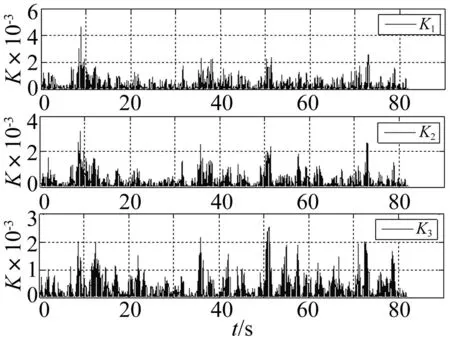
图32　方差贡献率动态曲线 Fig.32 Variance dedication rate dynamic curve

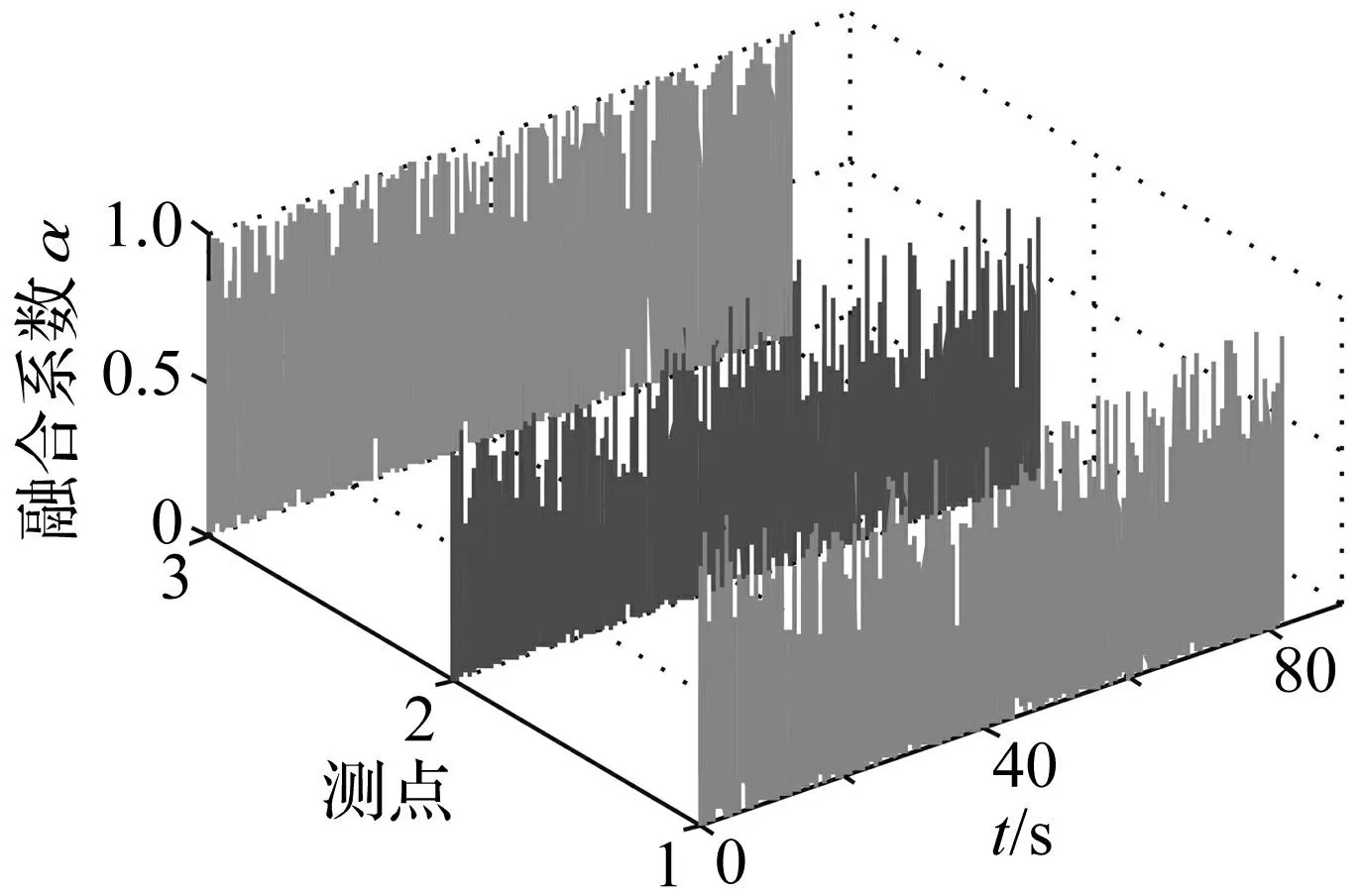
图33　融合系数动态曲线图 Fig.33 Fusion coefficient dynamic curve

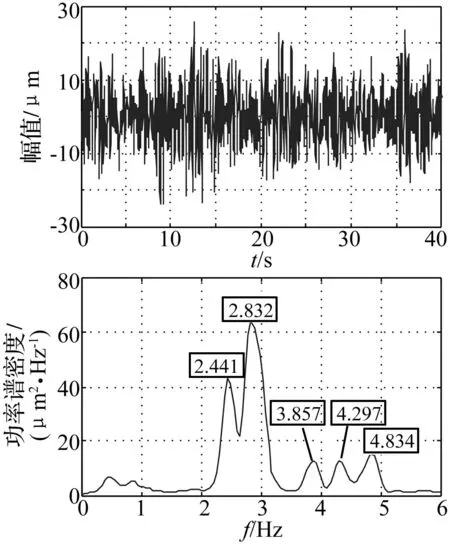
图34　基于方差贡献率动态融合信号时程线及其频谱图 Fig.34 The fusion signal and its spectrum based on variance dedication rate

结果表明，本文方法融合后信号含有5阶频率，分别为2.441Hz、2.832 Hz、3.857 Hz、4.297 Hz、4.834 Hz，融合后信号含有各个测点信号的频率成分，能够反映结构的整体振动特性，融合后信号各个频率成分含有的能量更加均衡，峰值更加清晰；而基于互相关融合方法的融合结果仅有2阶频率，出现了漏频现象。测点10信号中频率为4.297 Hz的频率与测点11信号中频率为4.248 Hz的模态实为结构同一阶模态，由于噪声的影响以及其它高能量频率成分的淹没效应，不同测点对同一阶频率的识别出现了偏差的现象，融合后信号该阶模态具有更加明显的峰值，其峰值为4.297Hz。由此可见，本文基于方差贡献率动态融合的信号频率成分更加完整，其频谱图各个峰值更显著，能够更全面的反映该工况下结构的整体振动特性。

4结论

针对传统数据融合算法对信号相似度要求高以及固定融合系数的缺陷，本文提出了基于方差贡献率的泄流结构动态响应多测点数据融合算法。通过数学模拟信号验证以及蜀河闸墩原型观测数据多测点信号融合应用，结果表明：

(1)该算法可将泄流结构多测点振动响应信号融合为一个能够反映结构整体振动特性的信号，该信号具有更加全面、准确的频率成分。

(2)基于方差贡献率的泄流结构动态响应数据融合算法能够均衡各个频率成分有效信号的能量，降低噪声干扰，同时避免模态淹没的现象。

(3)与基于互相关融合算法相比，基于方差贡献率的泄流结构动态响应数据融合算法具有较好的信息提取能力，其动态融合模式更加灵活，在泄流结构振动响应多测点数据级融合方面具有较好的应用前景。

参考文献

[1]Hall D L,Llinas J.Handbook of multisensor data fusion[M].BeiJing：Publishing House of Electronics Industry，2008.

[2]Luo R C, Lin M H, Scherp R S. Dynamic multi-sensor data fusion system for intelligent robots [ J] . IEEE Journal o f Robotics and Automation,1988, 4(4):386-396.

[3]焦莉, 李宏男. 基于数据融合和小波分析的结构损伤诊断[ J] . 振动与冲击, 2006, 25(5):85-88.

JIAO Li, LI Hong-nan. Diagnosis of structural damage based on data fusion and wavelet analysis method[J]. Journal of Vibration and Shock, 2006,25(5):85-88.

[4]李学军，李 萍，褚福磊. 基于相关函数的多振动信号数据融合方法[J]. 振动、测试与诊断，2009,29(2):179-183.

LI Xue-jun, LI Ping,CHU Fu-lei. Data fusion of multi-sensor vibration signal using correlation function[J]. Journal of Vibration, Measurement & Diagnosis, 2009,29(2):179-183.

[5]葛新成, 罗大成, 曹勇. 相关函数在数字信号处理中的应用[ J] . 电光与控制, 2006,13(6):78-80.

GE Xin-cheng, LUO Da-cheng, CAO Yong. Application of correlation function in digital signal processing[J]. Electronics Optics & Control, 2006,13(6):78-80.

[6]王济, 胡晓. Matlab在振动信号处理中的应用[ M] . 北京: 中国水利水电出版社, 2006: 114-117.

[7]Escamilla-Ambrosio P J,Mort N. Hybrid kalman filter-fuzzy logic adaptive multisensor data fusion architectures[C]//Proceedings of the 42nd IEEE Conference on Decision and Control,Maui, Hawaii USA, December 2003,5: 5215-5220.

[8]卢伟,滕军. 基于数据融合的传感器优化布置方法[J]. 振动与冲击，2009,28(9):52-55.

LU Wei, TENG Jun. A method of optimal sensor placement based on data fusion [J]. Journal of Vibration and Shock, 2009,28(9):52-55.

[9]谢志江, 王雪. 数据融合在机械故障诊断中的应用研究[J]. 振动与冲击，2003,22(2):11-13.

XIE Zhi-jiang, WANG Xue. Application study of data fusion in mechanical fault diagnosis [J]. Journal of Vibration and Shock, 2003,22(2):11-13.

[10]姜绍飞，胡春明. 基于模态指标与数据融合的钢管混凝土拱桥损伤识别[J]. 振动与冲击，2009,28(12):92-95.

JIANG Shao-fei, HU Chun-ming. Structural damage identification based on modal indices and data fusion for arch bridge of concrete-filled steel tubes[J].Journal of Vibration and Shock,2009,28(12):92-95.

[11]胡鑫，杨智春，王乐.基于振动响应内积向量和数据融合的结构损伤检测方法试验研究[J].振动与冲击,2013,32(14):109-115.

HU Xin,YANG Zhi-chun,WANG Le. Damage detection of a structure using a combined approach of IPV method and data fusion[J].Journal of Vibration and Shock,2013,32(14):109-115.

[12]侯立群,赵雪峰,欧进萍,等.结构损伤诊断不确定性方法研究进展[J].振动与冲击,2014,33(18):50-58.

HOU Li-qun,ZHAO Xue-feng,OU Jin-ping,et al.A review of nondeterministic methods for structural damage diagnosis[J].Journal of Vibration and Shock,2014,33(18):50-58.

[13]李成业，刘昉，马斌，等. 基于改进HHT的高拱坝模态参数识别方法研究[J]. 水力发电学报，2012，31(1)：48-55.

LI Cheng-ye, LIU Fan, MA Bin, et al.Study on modal parameters identification method of high arch dam based on improved Hilbert-Huang Transform [J]. Journal of Hydroelectric Engineering, 2012，31(1)：48-55.