自由搜索的BPNN在WSNs数据融合中的应用
谢佳华++刘军


摘 要:为了进一步提高无线传感器网络(WSNs)的能量利用效率、数据准确性和收集数据精度,需要对采集的数据进行融合。针对现有BP神经网络(BPNN)解决该问题存在容易陷入局部最优值的问题。文中把自由搜索(FS)算法和BP神经网络结合起来,充分发挥自由搜索算法的全局收敛性、自适应性、本质并行性优点。通过仿真实验并与BP神经网络相比较,该算法能有效减少通信量、提高数据准确性、延长网络生存时间,从而证明了该算法的有效性。
关键词:WSNs;数据融合;自由搜索算法;BP神经网络
中图分类号:TP393 文献标识码:A 文章编号:2095-1302(2015)11-00-03
0 引 言
无线通信技术、传感器技术、嵌入式计算技术、微电子技术等技术的发展和成熟,促成了无线传感器网络(Wireless Sensor Networks , WSNs)的产生[1,2]。WSNs广泛应用于国防军事、工业生产、精准农业、医疗健康、环境监测等领域[3]。
Nakamura E.F.等[4]对WSNs数据融合的模型、方法以及分类进行了研究;陈斌等[5]把神经网络和证据理论结合起来,建立了管道泄漏诊断模型;李志宇等[6]人提出的基于网格和移动代理的WSNs数据融合算法有较小的网络能耗和延时。但这些算法存在收敛速度慢,易陷入局部最优等缺点,所以本文提出一种自由搜索(Free Search,FS)和BP神经网络(Back Propagation Neural Network , BPNN)相结合的算法(FS-BF),优化数据融合性能,降低网络能量消耗,延长网络生存时间。
1 BP神经网络和自由搜索算法
为实现BPNN和自由搜索算法的结合,建立切实可行的WSNs数据融合优化模型,本节介绍了两个算法的优化过程。
1.1 BP神经网络
BPNN是一种单向传播的多层前馈网络,图1所示为一个三层BPNN示意图,包括输入层、隐层和输出层[7]。
图1 三层BPNN模型
设BPNN的输入n维向量X∈Rn,X=[x1,x2,…,xn]T,输出为m维向量Y∈Rm,Y=[y1,y2,…,ym],隐层共有l个神经元,则隐层输出为l维的向量Z∈Rl,Z=[z1,z2,…,zl],网络的输出为:
(1)
式(1)中,wij(0)和wij(1)分别为由输入层到隐层和隐层到输出层的连接权值,θi和φj分别为隐层和输出层的阈值。
一般情况下把Sigmoid函数作为传递函数。
(2)
输出层和前面各层的误差值可以通过如下公式计算:
(3)
(4)
对于隐含层和输出层神经元个数,可以参考下式确定:
隐含层: (5)
输出层:h=log2m (6)
其中,m为输入神经元个数,n为输出神经元个数,a为1-10之间的任意数。
1.2 自由搜索算法
FS算法的寻优过程包括初始化、搜索过程和终止三个步骤来确定目标函数的最优值[8]。
1.2.1 初始化
通过随机值产生初始种群,并生成初始信息素Pk。
x0ji=ximin+(ximax-ximin)·random (7)
式(7)中,j=1,2,…,m,表示第j只个体,i表示变量的第i维,i=1,2,…,n, x0ji为动物个体j的初始位置,ximax和ximin为搜索空间的边界,即个体j在第i维上的最大值和最小值。random为(0,1)之间的随机数。
1.2.2 搜索过程
(1)计算灵敏度,灵敏度定义如下:
Si=Smin+ΔSj (8)
ΔSj=(Smax-Smin)·randomj (9)
Smax和Smin为灵敏度的最大值和最小值。
(2)确定初始点,选择新一轮搜索起始点。
(10)
k是标记信息素的坐标点。
(3)更新个体位置。
xtji =x0ji-Δxtji +2Δxtji randomtji (11)
xtji为更新后个体的位置分量,t为当前步伐数,t=1,2,…,T,T为每次行走的最大步伐数;randomtji为介于(0,1)的随机数;修改策略Δxtji 按下式确定:
Δxtji =Rji (xmaxi-xmini)randomtji (12)
式(12)中,Rji 表示领域距离,Rji∈(Rmin,Rmax)。领域距离体现着个体的灵活性,受整个搜索空间的约束。
可按如下两式定义个体的行为:
ftj=f(xtij) (13)
fj=maxf(xtj) (14)
其中,f(xtij) 是一个个体完成搜索步以后作标记的位置。
(4)释放信息素,信息素定义如下:
(15)
max(fi) 表示第j个个体的最佳值。并且规定:Smin=Pmin,Smax=Pmax。
新一轮的搜索起始点由如下公式确定:
(16)
1.2.3 终止条件
可以有以下三种方式终止算法:
(1)寻优方式 fmax≥f0
fmax为搜索的最优值,f0为可接受的期望值。
(2)迭代方式 g≥G
g为当前的迭代数,G为限制的最大迭代数。
(3)复合方式,即满足(1)和(2)中的一种终止算法。
BPNN主要存在三个缺陷:一是局部极小点问题,二是收敛速度慢的问题,三是隐含层神经元节点个数难以确定的问题。而自由搜索算法具有全局搜索特性以及比其他算法收敛速度快的优点弥补了BPNN前两个不足,故本文尝试把自由搜索算法和BPNN结合起来,优化WSNs数据融合的效果。
2 FS-BP在WSNs数据融合中的应用
2.1 WSN数据融合模型
本节主要是建立以BPNN为主体的汇聚节点数据融合模型,其数据融合的过程如图2所示。该模型系统包括无线传感器子系统和汇聚节点数据融合处理子系统两大部分。前者主要是由传感器节点组成,每个节点可以有一个或者多个传感器采集相关数据,后者包括数据预处理和数据融合两个步骤,其中预处理的作用是把有用数据分离出来,而数据融合是接收预处理后的数据,然后把数据输入到已训练好的BPNN中进行融合并得出融合结果。另外,汇聚节点把原始数据信息和融合结果存储起来,便于对比分析融合结果和原始信息,方便进行必要的反馈调节。
图2 数据融合模型
2.2 FS-BP算法
算法构建的主要思想是:针对BPNN初始值敏感、收敛速度慢以及易陷入局部最优解的缺点,利用FS代替BPNN中的梯度修正,搜索符合既定条件的权值,提高算法性能。具体方法描述如下:
神经网络的初值权重按照传统的常规办法生成,用wi(i=1,2,…,m)表示任意一组完整的wi。一个动物个体,则有m个这样的个体,所以m为种群的大小。优化目标函数为均方误差函数:
(17)
上式中,E为均方误差,N为样本个数,yid为第i个预期输出值,yi为第i个实际输出值。
FS搜索的任务是通过对公式(17)的优化,得到该函数的最小值,找出均方误差最小的网络权重, 再输入到BPNN各层中。该算法的主要流程如图3所示。
利用FS算法对初始权值进行优化处理后,把输出的权值输入到神经网络。本文采用三层BPNN模型,结合BPNN理论和所建立的数据融合模型,FS-BPNN算法的具体步骤如下:
①初始化参数,包括神经网络的结构、初始权值、迭代次数上限、误差阈值、学习速率、学习样本以及FS的种群大小,步伐数和小步数以及邻居距离。
②随机选取训练一对数据,将输入向量加到输入层。
③利用关系式(1)输出每一层和输出层的输出值。
④采用公式(3)(4)输出层和前面各层的实际输出和要求的目标值的误差。得到的误差值若小于阈值,则转⑥,否则转步骤 ⑤。
⑤利用FS算法优化公式(17),搜索符合条件的权值,并返回③。
⑥ 结束。
图3 网络参数优化流程图
3 算法仿真
采用三层BPNN模型,输入神经元个数与传感器节点数相同,隐含层神经元个数按公式(6)确定,输出层神经元个数按公式(7)确定。仿真环境为Matlab,版本为R2008a。
3.1 参数设置
相关的参数设置如表1所列。
表1 参数设置表参数 取值 参数 取值
区域大小 50 m×50 m 种群规模 120
传感器节点数 120 终止代数G 500
网络拓扑 随机部署 搜索小步数T 120
节点通信半径 20 m 搜索半径Rji 0.01,0.5,1
节点感知半径 10 m 误差阈值 10-3
节点初始能量 0.7 J 训练速率系数 0.3
数据传输能耗 20 nJ/bit 数据接收能耗 12 nJ/bit
3.2 仿真实验
为了尽可能全面验证算法的有效性和可行性,本文从以下三个角度设置仿真实验。
3.2.1 仿真实验1——网络的收敛性
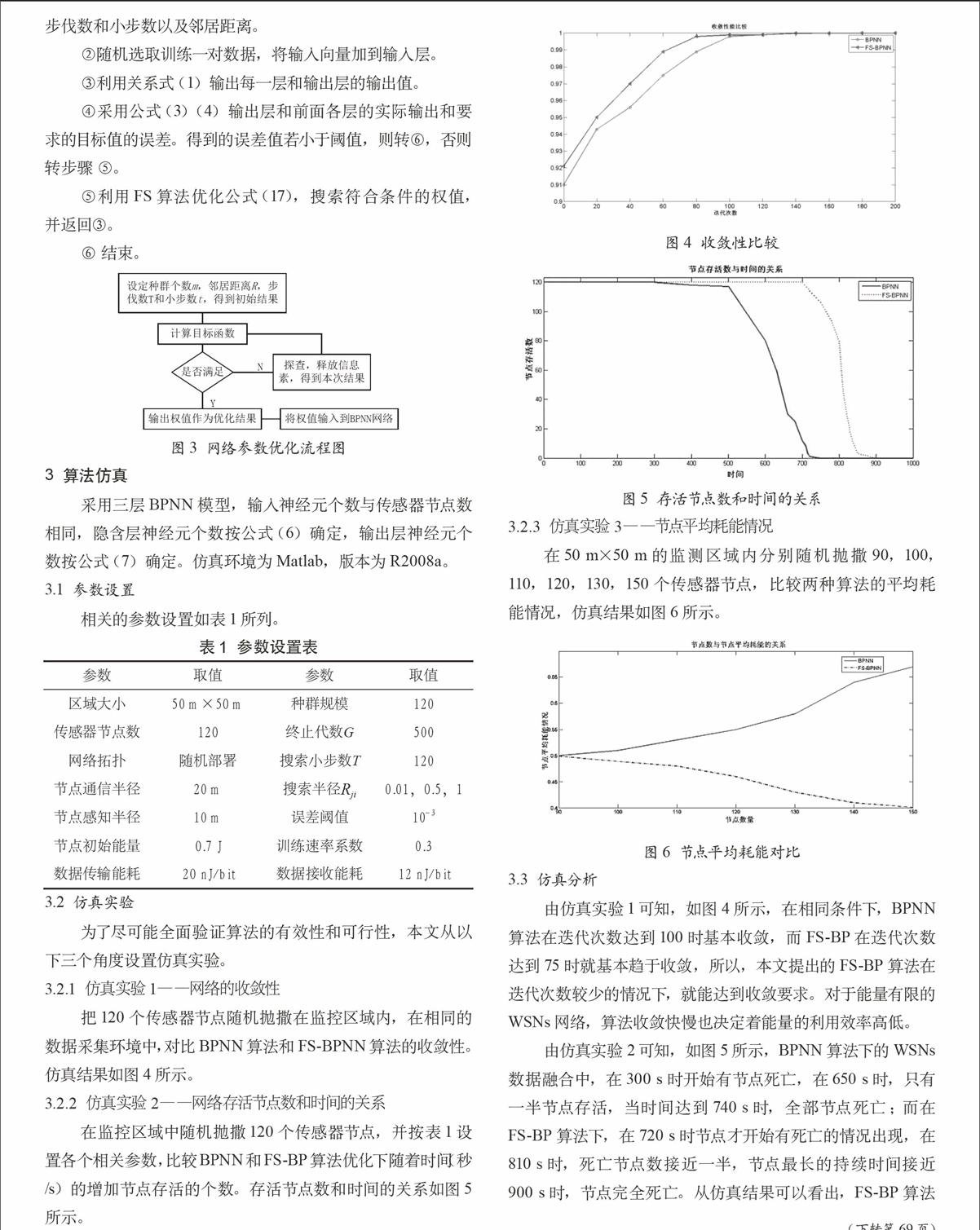
把120个传感器节点随机抛撒在监控区域内,在相同的数据采集环境中,对比BPNN算法和FS-BPNN算法的收敛性。仿真结果如图4所示。
3.2.2 仿真实验2——网络存活节点数和时间的关系
在监控区域中随机抛撒120个传感器节点,并按表1设置各个相关参数,比较BPNN和FS-BP算法优化下随着时间(秒/s)的增加节点存活的个数。存活节点数和时间的关系如图5所示。
图4 收敛性比较
图5 存活节点数和时间的关系
3.2.3 仿真实验3——节点平均耗能情况
在50 m×50 m的监测区域内分别随机抛撒90,100,110,120,130,150个传感器节点,比较两种算法的平均耗能情况,仿真结果如图6所示。
图6 节点平均耗能对比
3.3 仿真分析
由仿真实验1可知,如图4所示,在相同条件下,BPNN算法在迭代次数达到100时基本收敛,而FS-BP在迭代次数达到75时就基本趋于收敛,所以,本文提出的FS-BP算法在迭代次数较少的情况下,就能达到收敛要求。对于能量有限的WSNs网络,算法收敛快慢也决定着能量的利用效率高低。
由仿真实验2可知,如图5所示,BPNN算法下的 WSNs数据融合中,在300 s时开始有节点死亡,在650 s时,只有一半节点存活,当时间达到740 s时,全部节点死亡;而在FS-BP算法下,在720 s时节点才开始有死亡的情况出现,在810 s时,死亡节点数接近一半,节点最长的持续时间接近900 s时,节点完全死亡。从仿真结果可以看出,FS-BP算法比BPNN算法更能延长网络运行时间,特别是网络的正常工作时间。
由仿真实验3可知,BPNN算法随着节点数的增加,平均每个节点的耗能也随着增加,而FS-BP算法却随着节点数的增加而减少,且两者之间的差距逐渐加大,这从另一个方面体现了FS-BP算法性能的优越性和有效性。
综上所述,在WSNs数据融合中,FS-BP算法比BPNN算法的性能更好,不仅提高了收敛速度和能量利用效率,还有效延长了网络的生存时间。
4 结 语
数据融合作为延长WSNs生存时间的一种重要方法,是WSNs研究的重要领域之一。本文提出把FS算法与BPNN算法相结合,解决BPNN算法收敛速度慢的问题,通过建立模型,并从多个角度设置仿真实验验证算法的有效性,结果表明,FS-BP算法能够像预期的一样加快收敛速度,降低节点能量消耗,从而延长网络的生存时间。下一步的研究应该进一步结合具体应用背景的特点,改进算法,提高WSNs数据融合的实际应用效果。
参考文献
[1] Ian F. Akyildiz, Mehmet Can Vuran.Wireless Sensor Networks[M]. John Wiley & Sons Ltd,2010.
[2] 孙利明,李建中,陈瑜,等.无线传感器网络[M].北京:清华大学出版社,2005: 149-151.
[3] Akyildiz I F, Su W, Sankarasubramaniam Y, et al.Wireless sensor networks: a survey[J].Computer networks, 2002, 38(4): 393-422.
[4] Nakamura E.F., Louxeiro A.A.F.,Frery A.C.Information fusion for wireless sensor networks : Methods, models, and classifications[J].Acm Computing Surveys,2007,39(3).
[5] 陈斌, 万江文, 吴银锋,等. 神经网络和证据理论融合的管道泄漏诊断方法[J].北京邮电大学学报, 2009, 32(1):1007-1021.
[6] 李志宇, 史浩山.一种基于网格和移动代理的无线传感器网络数据融合算法[J].传感技术学报, 2008, 21(7):1232-1236.
[7] 王晓荣,伦淑娴.基于改进粒子群算法的BP神经网络优化研究[J].渤海大学学报:自然科学版, 2008,29(2):189-193.
[8] Kalin P, Guy L.Free search-a comparative analysis[J].Information Science, 2005, 172(2): 173-193.

